Data Prefetch and Software Pipelining Stanford University CS

Data Prefetch and Software Pipelining Stanford University CS 243 Winter 2006 Wei Li 1

Agenda Data Prefetch n Software Pipelining n Stanford University CS 243 Winter 2006 2

Why Data Prefetching Increasing Processor – Memory “distance” n Caches do work !!! … IF … n n n Data set cache-able, accesses local (in space/time) Else ? … Stanford University CS 243 Winter 2006 3

Data Prefetching n What is it ? Request for a future data need is initiated n Useful execution continues during access n Data moves from slow/far memory to fast/near cache n Data ready in cache when needed (load/store) n Stanford University CS 243 Winter 2006 4

Data Prefetching n When can it be used ? n n Future data needs are (somewhat) predictable How is it implemented ? in hardware: history based prediction of future access n in software: compiler inserted prefetch instructions n Stanford University CS 243 Winter 2006 5

Software Data Prefetching Compiler scheduled prefetches n Moves entire cache lines (not just datum) n n n Typically a non-faulting access n n Spatial locality assumed – often the case Compiler free to speculate prefetch address Hardware not obligated to obey A performance enhancement, no functional impact n Loads/store may be preferentially treated Stanford University n CS 243 Winter 2006 6

Software Data Prefetching Use n Mostly in Scientific codes n Vectorizable loops accessing arrays deterministically n Data access pattern is predictable n Prefetch scheduling easy (far in time, near in code) n Large working data sets consumed n Even large caches unable to capture access locality n Sometimes in Integer codes Loops with pointer de-references Stanford University n CS 243 Winter 2006 7

Selective Data Prefetch j do j = 1, n A do i = 1, m A(i, j) = B(1, i) + B(1, i+1) i enddo n E. g. A(i, j) has spatial locality, therefore only one prefetch is required for every cache line. Stanford University B CS 243 Winter 2006 1 1 m 8

Formal Definitions Temporal locality occurs when a given reference reuses exactly the same data location n Spatial locality occurs when a given reference accesses different data locations that fall within the same cache line n Group locality occurs when different references access the same cache line n Stanford University CS 243 Winter 2006 9

Prefetch Predicates If an access has spatial locality, only the first access to the same cache line will incur a miss. n For temporal locality, only the first access will incur a cache miss n If an access has group locality, only the leading reference incurs cache miss. n If an access has no locality, it will miss in every iteration. n Stanford University CS 243 Winter 2006 10

Example Code with Prefetches do j = 1, n do i = 1, m A(i, j) = B(1, i) + B(1, i+1) if (iand(i, 7) == 0) prefetch (A(i+k, j)) if (j == 1) prefetch (B(1, i+t)) enddo Assumed CLS = 64 bytes and data size = 8 bytes j A i B 1 1 m k and t are prefetch distance values Stanford University CS 243 Winter 2006 11

Spreading of Prefetches If there is more than one reference that has spatial locality within the same loop nest, spread these prefetches across the 8 -iteration window n Reduces the stress on the memory subsystem by minimizing the number of outstanding prefetches n Stanford University CS 243 Winter 2006 12

Example Code with Spreading do j = 1, n do i = 1, m C(i, j) = D(i-1, j) + D(i+1, j) if (iand(i, 7) == 0) prefetch (C(i+k, j)) if (iand(i, 7) == 1) prefetch (D(i+k+1, j)) enddo Stanford University j C, D i Assumed CLS = 64 bytes and data size = 8 bytes k is the prefetch distance value CS 243 Winter 2006 13

Prefetch Strategy Conditional Example loop Conditional Prefetching L: Load A(I) Load B(I). . . I = I + 1 Br L, if I<n L: Load A(I) Load B(I) Cmp p. A=(I mod 8 == 0) if(p. A) prefetch A(I+X) Cmp p. B=(I mod 8 == 1) If(p. B) prefetch êCode for condition B(I+X). . . generation I = I + 1 Br L, if I<n êPrefetches occupy issue slots Stanford University CS 243 Winter 2006 14

Prefetch Strategy - Unroll Example loop L: Load A(I) Load B(I). . . I = I + 1 Br L, if I<n Unrolled Unr_Loop: prefetch A(I+X) load A(I) load B(I). . . prefetch B(I+X) load A(I+1) load B(I+1). . . prefetch C(I+X) load A(I+2) load B(I+2). . . prefetch D(I+X) load A(I+3) load B(I+3) êCode bloat (>8 X) êRemainder loop Stanford University CS 243 Winter 2006 . . . prefetch E(I+X) load A(I+4) load B(I+4). . . load A(I+5) load B(I+5). . . load A(I+6) load B(I+6). . . load A(I+7) load B(I+7). . . I = I + 8 Br Unr_Loop, if I<n 15

Software Data Prefetching Cost n Requires memory instruction resources n n A prefetch instruction for each access stream Issues every iteration, but needed less often If branched around, inefficient execution results n If conditionally executed, more instruction overhead results n If loop is unrolled, code bloat results n Stanford University CS 243 Winter 2006 16

Software Data Prefetching Cost n Redundant prefetches get in the way n n Resources consumed until prefetches discarded! Non redundant need careful scheduling n Resources overwhelmed when many issued & miss Stanford University CS 243 Winter 2006 17

Desirable Characteristics n Uses minimal instruction resources n n Minimizes redundant prefetches n n No code bloat, no prefetch branches Issues prefetches spaced in time n n One prefetch instruction for multiple streams Machine resources utilized evenly Solution: rotating register prefetch if there is HW support. Stanford University CS 243 Winter 2006 18

• Register Rotating Registers rotation provides an automatic renaming mechanism. • Instructions contain a “virtual” register number 32 33 34 35 36 37 38 39 Iteration 1 r 32 r 33 r 34 r 35 r 36 r 37 r 38 r 39 Iteration 2 r 33 r 34 r 35 r 36 r 37 r 38 r 39 r 32 Iteration 3 r 34 r 35 r 36 r 37 r 38 r 39 r 32 r 33 Stanford University CS 243 Winter 2006 19

Rotating Reg Prefetch Illustrated Example loop Orig_loop: Load A(I) Load B(I) Load C(I) Load D(I) Load E(I). . . I = I + 1 Br Orig_loop, if I<n éSingle prefetch inst éNo loop unrolling éAt most 1 miss/iter Stanford University Rotating Register Prefetching r 33 = address of E(1+X) r 34 = address of D(1+X) r 35 = address of C(1+X) r 36 = address of B(1+X) r 37 = address of A(1+X) Method 1 Loop: prefetch [r 37] r 32 = r 37 + INCR. . . load A(I) load B(I) load C(I) load D(I) load E(I). . . I = I + 1 Br Method 1 Loop, if I<n CS 243 Winter 2006 20

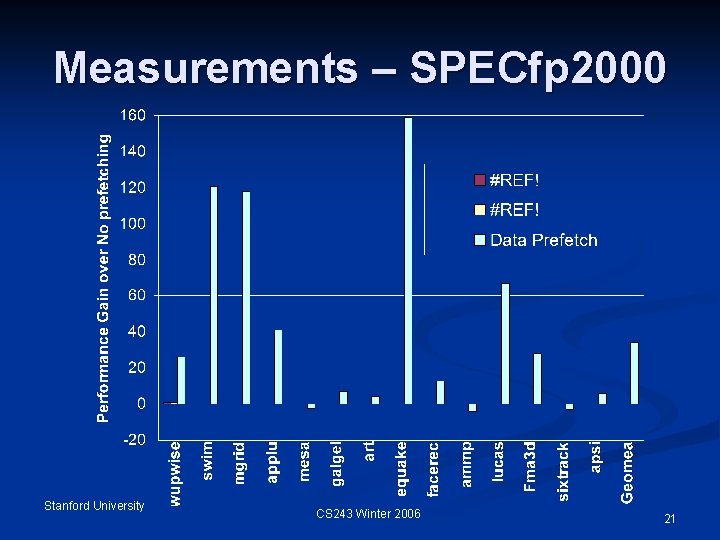
Measurements – SPECfp 2000 Stanford University CS 243 Winter 2006 21

Agenda Data Prefetch n Software Pipelining n Stanford University CS 243 Winter 2006 22

Software Pipelining Obtain parallelism by executing iterations of a loop in an overlapping way. n We’ll focus on simplest case: the do-all loop, where iterations are independent. n Goal: Initiate iterations as frequently as possible. n Limitation: Use same schedule and delay for each iteration. n Stanford University CS 243 Winter 2006 23

Machine Model Timing parameters: LD = 2, others = 1 clock. n Machine can execute one LD or ST and one arithmetic operation (including branch) at any one clock. n n I. e. , we’re back to one ALU resource and one MEM resource. Stanford University CS 243 Winter 2006 24

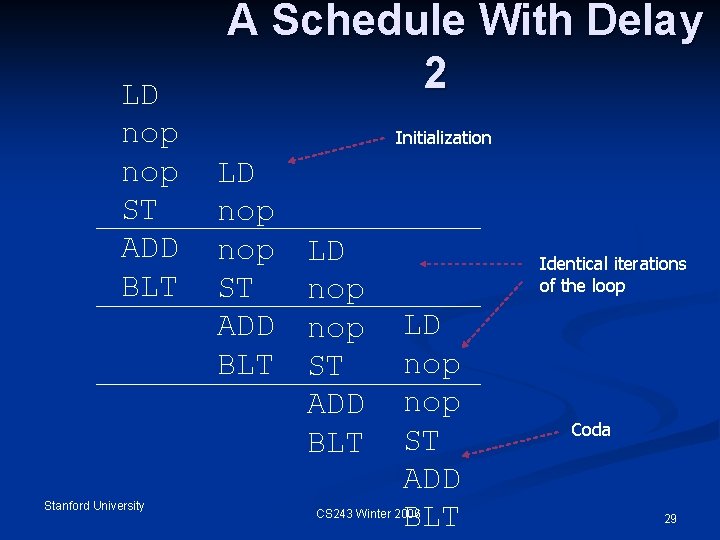
Example for (i=0; i<N; i++) B[i] = A[i]; n r 9 holds 4 N; r 8 holds 4*i. L: LD r 1, a(r 8) nop ST b(r 8), r 1 ADD r 8, #4 BLT r 8, r 9, L Stanford University CS 243 Winter 2006 Notice: data dependences force this schedule. No parallelism is possible. 25

Let’s Run 2 Iterations in Parallel n Focus on operations; worry about registers later. LD nop LD ST nop Oops --- violates ADD ST ALU resource constraint. BLT ADD BLT Stanford University CS 243 Winter 2006 26

Introduce a NOP LD nop ST ADD nop BLT Stanford University LD nop ST ADD nop BLT CS 243 Winter 2006 Add a third iteration. Several resource conflicts arise. 27

Is It Possible to Have an Iteration Start at Every Clock? Hint: No. n Why? n An iteration injects 2 MEM and 2 ALU resource requirements. n n n If injected every clock, the machine cannot possibly satisfy all requests. Minimum delay = 2. Stanford University CS 243 Winter 2006 28

LD nop ST ADD BLT Stanford University A Schedule With Delay 2 Initialization LD nop nop ST ADD BLT Identical iterations of the loop LD nop ST ADD BLT CS 243 Winter 2006 Coda 29

Assigning Registers We don’t need an infinite number of registers. n We can reuse registers for iterations that do not overlap in time. n But we can’t just use the same old registers for every iteration. n Stanford University CS 243 Winter 2006 30

Assigning Registers --- (2) n The inner loop may have to involve more than one copy of the smallest repeating pattern. n n Enough so that registers may be reused at each iteration of the expanded inner loop. Our example: 3 iterations coexist, so we need 3 sets of registers and 3 copies of the pattern. Stanford University CS 243 Winter 2006 31

Example: Assigning Registers n Our original loop used registers: r 9 to hold a constant 4 N. n r 8 to count iterations and index the arrays. n r 1 to copy a[i] into b[i]. n n The expanded loop needs: r 9 holds 12 N. n r 6, r 7, r 8 to count iterations and index. n r 1, r 2, r 3 to copy certain array elements. n Stanford University CS 243 Winter 2006 32

The Loop Body Each register handles every third element of the arrays. To break the loop early Iteration i L: ADD BGE LD nop ST r 8, #12 r 8, r 9, L’ r 1, a(r 8) b(r 8), r 1 Iteration i + 3 Iteration i + 1 nop ST ADD BGE LD nop b(r 7), r 2 r 7, #12 r 7, r 9, L’’ r 2, a(r 7) Iteration i + 2 LD nop ST ADD BLT r 3, a(r 6) b(r 6), r 3 r 6, #12 r 6, r 9, L Iteration i + 4 L’ and L’’ are places for appropriate codas. Stanford University CS 243 Winter 2006 33

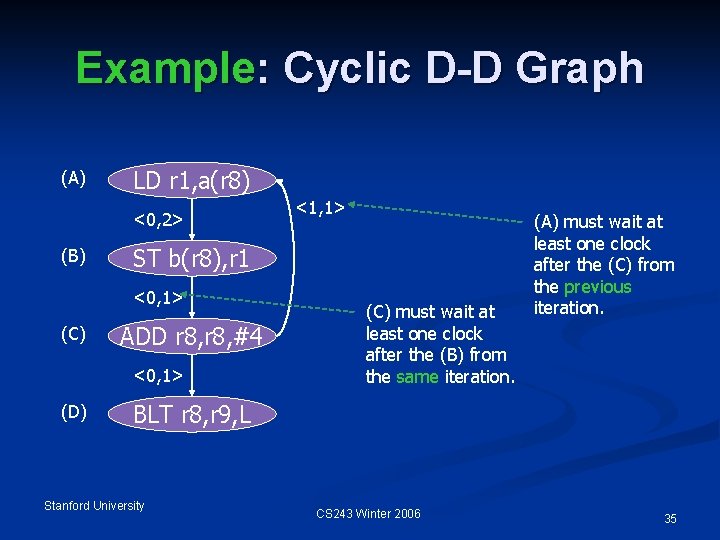
Cyclic Data-Dependence Graphs n We assumed that data at an iteration depends only on data computed at the same iteration. n Not even true for our example. n r 8 computed from its previous iteration. n But it doesn’t matter in this example. n Fixup: edge labels have two components: (iteration change, delay). Stanford University CS 243 Winter 2006 34

Example: Cyclic D-D Graph (A) LD r 1, a(r 8) <0, 2> (B) ST b(r 8), r 1 <0, 1> (C) ADD r 8, #4 <0, 1> (D) <1, 1> (C) must wait at least one clock after the (B) from the same iteration. (A) must wait at least one clock after the (C) from the previous iteration. BLT r 8, r 9, L Stanford University CS 243 Winter 2006 35

Matrix of Delays Let T be the delay between the start times of one iteration and the next. n Replace edge label <i, j> by delay j-i. T. n Compute, for each pair of nodes n and m the total delay along the longest acyclic path from n to m. n Gives upper and lower bounds relating the times to schedule n and m. n Stanford University CS 243 Winter 2006 36

Example: Delay Matrix A A C D 2 B C B A A 1 1 -T 1 D 2 B 2 -T C 1 -T 3 -T C D 3 4 1 2 1 D Edges Acyclic Transitive Closure Note: Implies T ≥ 4 (because only one register used for loop-counting). If T=4, then A (LD) must be 2 clocks before B (ST). If T=5, A can be 2 -3 clocks before B. Stanford University B CS 243 Winter 2006 S(B) ≥ S(A)+2 S(A) ≥ S(B)+2 -T S(B)-2 ≥ S(A) ≥ S(B)+2 -T 37

Iterative Modulo Scheduling n Compute the lower bounds (MII) on the delay between the start times of one iteration and the next (initiation interval, aka II) due to resources n due to recurrences n Try to find a schedule for II = MII n If no schedule can be found, try a larger II. n Stanford University CS 243 Winter 2006 38

Summary n References for compiler data prefetch: n n Todd Mowry, Monica Lam, Anoop Gupta, “Design and evaluation of a compiler algorithm for prefetching”, in ASPLOS’ 92, http: //citeseer. ist. psu. edu/mowry 92 design. html. Gautam Doshi, Rakesh Krishnaiyer, Kalyan Muthukumar, “Optimizing Software Data Prefetches with Rotating Registers”, in PACT’ 01, http: //citeseer. ist. psu. edu/670603. html. Stanford University CS 243 Winter 2006 39