DATA Not Just a Lot of Numbers James

DATA (Not Just a Lot of Numbers) James Stewart Lothar Redlin Saleem Watson

College Algebra A Course in Crisis? Introductory collegiate mathematics is in the midst of a revolution… -Nancy Baxter Hastings, Dickinson College Traditional College Algebra is a boring, archaic, torturous course that does not help students solve problems or become better citizens. It turns off students and discourages them from seeking more mathematics learning. - Chris Arney, Dean of Science and Mathematics, St. Rose College

College Algebra A Course in Crisis? NSF conference on “Rethinking the Courses Below Calculus” in Washington D. C in 2001. Some of the major themes to emerge from this conference: • Spend less time on algebraic manipulation and more time on exploring concepts • Reduce the number of topics but study those topics covered in greater depth • Give greater priority to data analysis as a foundation for mathematical modeling • Emphasize the verbal, numerical, graphical and symbolic representations of mathematical concepts

WHY DATA? Over the past two decades computers have transformed public discourse by generating piles of data and myriad analyses of these data. Ordinary citizens must deal with numbers and data every day. -Bernard Madison, University of Arkansas Virtually any educated individual will need the ability: 1. to examine a set of data and recognize a behavioral pattern in it, 2. to assess how well a given functional model matches the data, 3. to recognize the limitations in the model, 4. to use the model to draw appropriate conclusions, 5. to answer approriate questions about the phenomenon being studied. -Sheldon Gordon, Farmingdale State University of New York

WHY DATA? • Data relate the real world and algebraic equations. • Students can collect data and make models from data. • Students can see how the model gives us information about the thing being modeled.
WHY DATA? Greater Depth: Connecting the Concepts
WHY DATA? Greater Depth: Connecting the Concepts
WHY DATA? Greater Depth: Connecting the Concepts

COLLECTING DATA • From classmates (measurements) Age, height, hand span, shoe size, hat size

COLLECTING DATA • Survey From classmates (Surveys) 1. What is the value (in cents) of the coins in your pocket or purse? _____ 2. How far is your daily commute to school (in miles)? _____ 3. How many siblings do you have (including yourself)? _____ 4. How many hours a week do you spend on the Internet? _____ 5. How many hours a week do you spend on homework? ____ 6. Rate your happiness. not happy very happy Rate your satisfaction with your school work. not satisfied very satisfied 7.

COLLECTING DATA • From simple experiments – Bridge science

COLLECTING DATA • From simple experiments – – How quickly can you name your favorite things How many words can you recall from a memorized list (after a day, a week, a month). Listing vegetables Memorizing a list

COLLECTING DATA • From simple experiments – How quickly does water leak from a tank? Toricelli’s Law The experiment Students performing the experiment

COLLECTING DATA • From simple experiments – Radioactive decay—modeled with pennies Radioactive Decay Coin Experiment

COLLECTING DATA • From the Internet – How many farms in the US? Farming in the 19 th century Farming in the 20 th century

COLLECTING DATA • From the Internet – Population Las Vegas 1900 Las Vegas 2000

COLLECTING DATA • From Journal Articles – Algebra and Alcohol Concentration (mg/ml) after 95% ethanol oral dose Time (hr) 15 ml 30 ml 45 ml 60 ml 0. 0. 0. 067 0. 032 0. 071 — — 0. 133 0. 096 0. 019 — — 0. 167 — — 0. 28 0. 30 0. 2 0. 13 0. 25 — — 0. 267 0. 17 0. 30 — — 0. 333 0. 16 0. 31 0. 42 0. 46 0. 417 0. 17 — — — 0. 5 0. 16 0. 41 0. 59 0. 667 — — 0. 61 0. 66

DATA
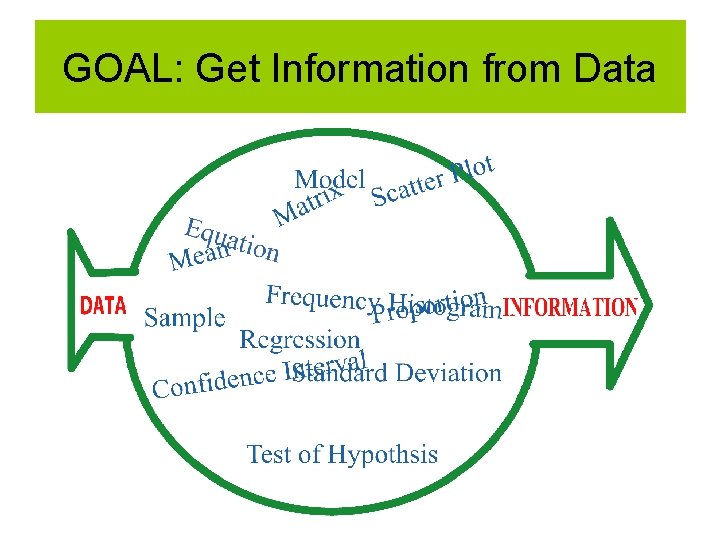
GOAL: Get Information from Data

Getting Information from Data • Descriptive Information Tells us something about the data itself • Inferential Information Tells us how to extend the information obtained from the data beyond the domain of the data.

The FORM of the Data How does the data obtained from this survey differ for different questions? • • • What is your age? What is your height? What is your hair color? From which source do you mostly obtain the news? Do you believe that the Universe began in a huge explosion?

The Form of the Data The form of the data tells us the kind of information we can obtain. • One-Variable Data • Two-Variable Data • Categorical Data • Sample Data

One-Variable Data Age (yr) 2 2 2 3 Income ( thousands of dollars) Selling Price (X 1000) 159 3 3 4 280 56 193 167 4 4 59 172 4 62 169 4 5 51 216 169 172

One-Variable Data Descriptive Information • Summary statistics: Central tendency: Mean, median Dispersion: variance, standard deviation

One-Variable Data Example: height of students Mean: 60”, S. D. : 10” Given this information, which picture is more likely?

One-Variable Data Descriptive Information • Frequency histogram Graphical, gives more complete information—tells how the data is distributed.
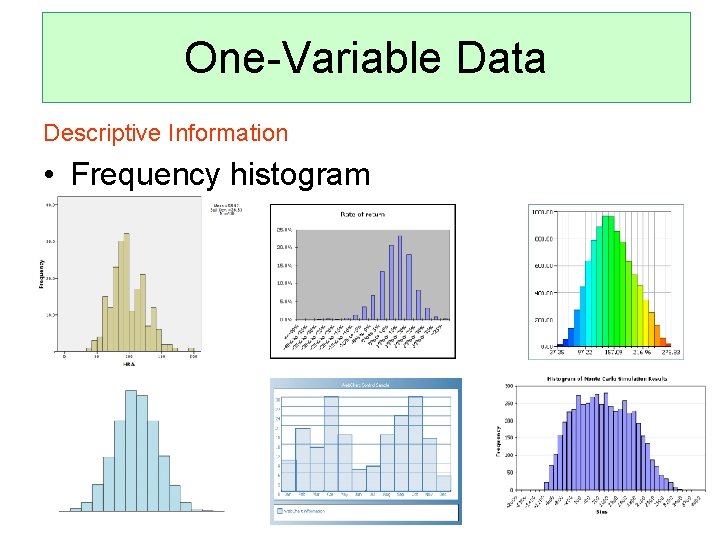
One-Variable Data Descriptive Information • Frequency histogram
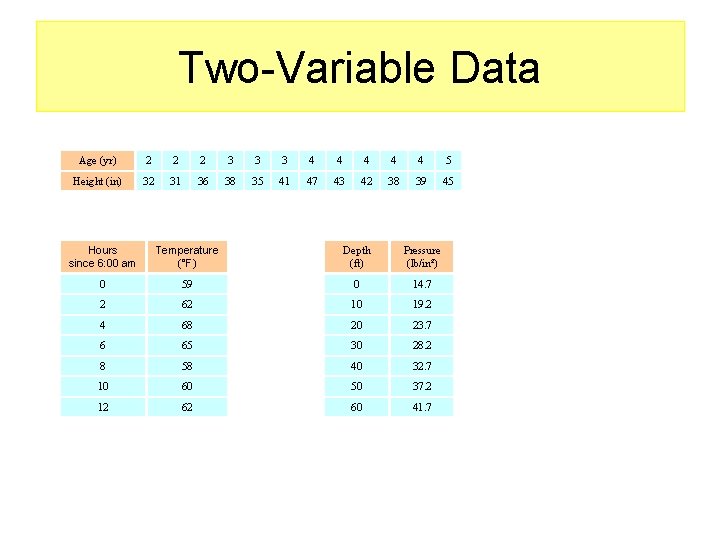
Two-Variable Data Age (yr) 2 2 2 3 3 3 4 4 4 5 Height (in) 32 31 36 38 35 41 47 43 42 38 39 45 Hours since 6: 00 am Temperature (°F) Depth (ft) Pressure (lb/in²) 0 59 0 14. 7 2 62 10 19. 2 4 68 20 23. 7 6 65 30 28. 2 8 58 40 32. 7 10 60 50 37. 2 12 62 60 41. 7

Two-Variable Data Descriptive Information • Scatter plot Gives description of the relationship between the variables. • Regression Line (or other curve) Gives the curve that best fits (or best describes) the data
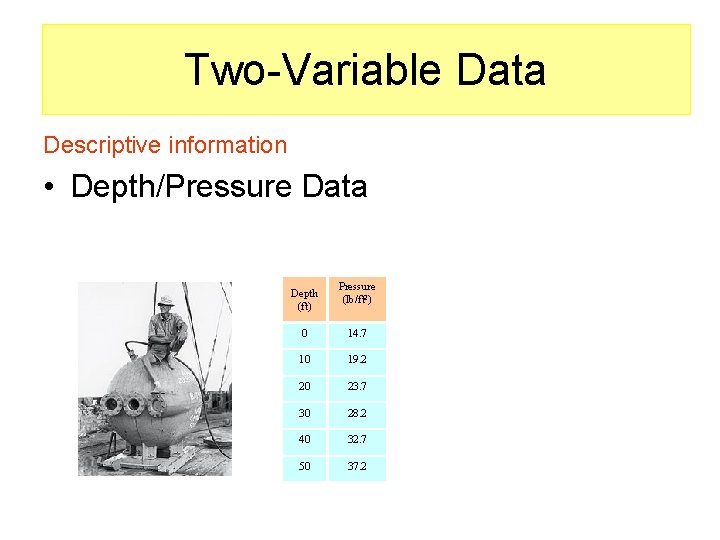
Two-Variable Data Descriptive information • Depth/Pressure Data Depth (ft) Pressure (lb/ft 2) 0 14. 7 10 19. 2 20 23. 7 30 28. 2 40 32. 7 50 37. 2

Two-Variable Data Descriptive information • TV Hours/BMI Hours TV BMI 0 15 0 17 . 5 15 . 5 18 . 75 16 1 15 1 17 1. 25 18 1. 5 19 : :

Two-variable data Two-Variable Data (Goal: Find a relationship between the variables) Descriptive Information • Regression Line (or other curve) Gives the curve that best fits (or best describes) the data Depth / Pressure Hours TV / BMI

Two-variable data Two-Variable Data (Goal: Find a relationship between the variables) Inferential Information • Regression Line (or other curve) Use the curve to get information not in the data (extrapolation or interpolation using the regression curve).
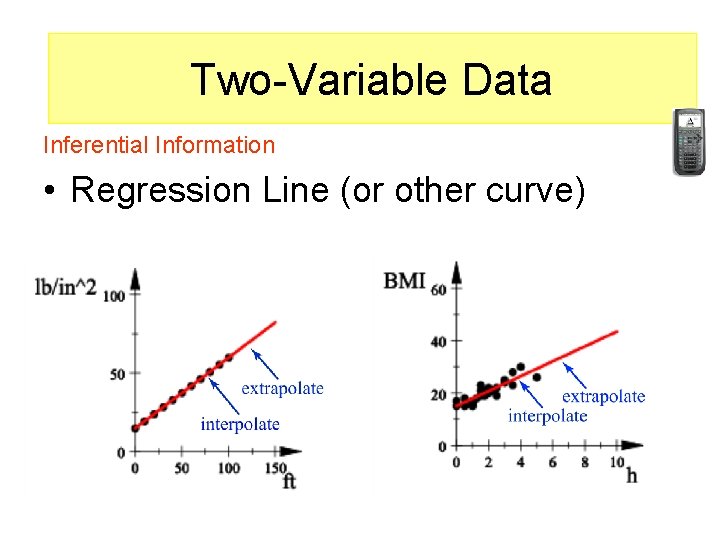
Two-variable data Two-Variable Data (Goal: Find a relationship between the variables) Inferential Information • Regression Line (or other curve)
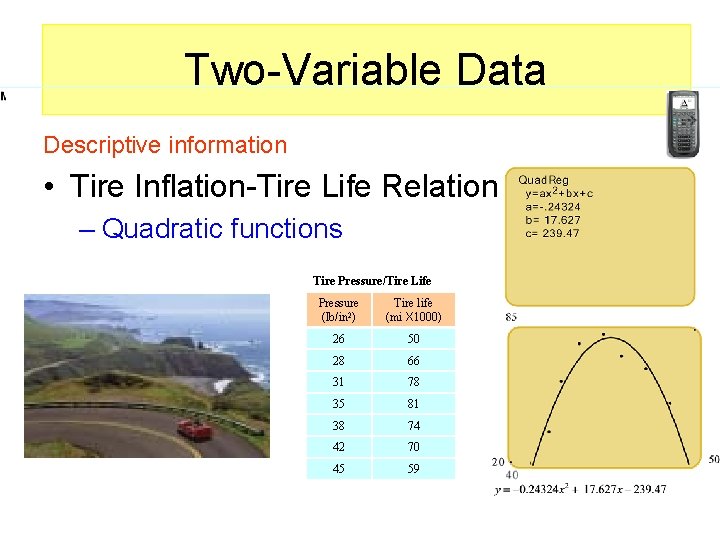
a Two-Variable Data Descriptive information • Tire Inflation-Tire Life Relation – Quadratic functions Tire Pressure/Tire Life Pressure (lb/in 2) Tire life (mi X 1000) 26 50 28 66 31 78 35 81 38 74 42 70 45 59

a Two-Variable Data Descriptive information • Species-Area Relation – Power functions Species-area data Cave Area (m 2) Number of species La Escondida 18 1 El Escorpion 19 1 El Tigre 58 1 Mision Imposible 60 2 San Martin 128 5 El Arenal 187 4 La Ciudad 344 6 Virgen 511 7

(a) a Two-Variable Data Descriptive information • Length-at-Age Relation – Polynomial functions Length-at-age data 90 year old rock fish Age (years) Length (inches) Ag e (ye ars) Length (inches) 1 4. 8 9 18. 2 2 8. 8 9 17. 1 2 8. 0 10 18. 8 3 7. 9 10 19. 5 4 11. 9 11 18. 9 5 14. 4 12 21. 7 6 14. 1 12 21. 9 6 15. 8 13 23. 8 7 15. 6 14 26. 9 8 17. 8 14 25. 1
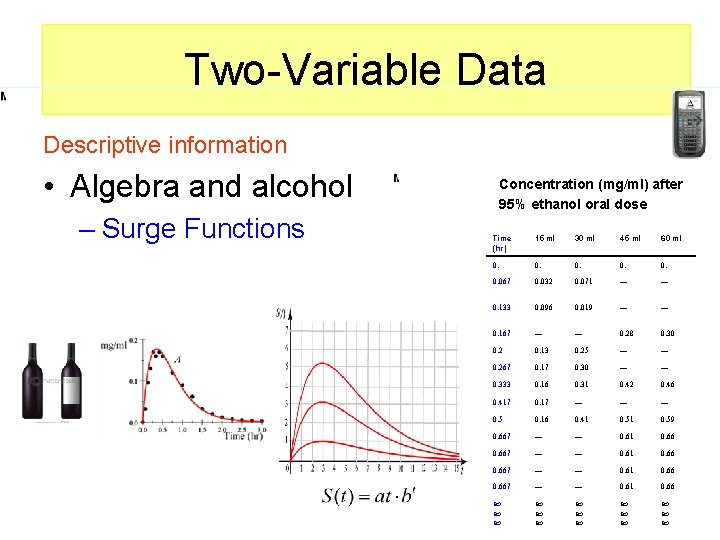
Two-Variable Data Descriptive information • Algebra and alcohol – Surge Functions Concentration (mg/ml) after 95% ethanol oral dose Time (hr) 15 ml 30 ml 45 ml 60 ml 0. 0. 0. 067 0. 032 0. 071 — — 0. 133 0. 096 0. 019 — — 0. 167 — — 0. 28 0. 30 0. 2 0. 13 0. 25 — — 0. 267 0. 17 0. 30 — — 0. 333 0. 16 0. 31 0. 42 0. 46 0. 417 0. 17 — — — 0. 5 0. 16 0. 41 0. 59 0. 667 — — 0. 61 0. 66

Categorical Data Results of survey: Student Number Hair color Eye Color 1 Dark Brown 2 Blond Brown 3 Dark Blue These data need organizing!

Categorical data Categorical (Goal: Organize the data/Get. Data information) Descriptive information • Organize Data in a Matrix

Categorical data Categorical (Goal: Organize the data/Get. Data information) Descriptive information • Organize Data in a Proportionality Matrix

Categorical data Categorical (Goal: Organize the data/Get. Data information) Get information from the data • Using matrix multiplication
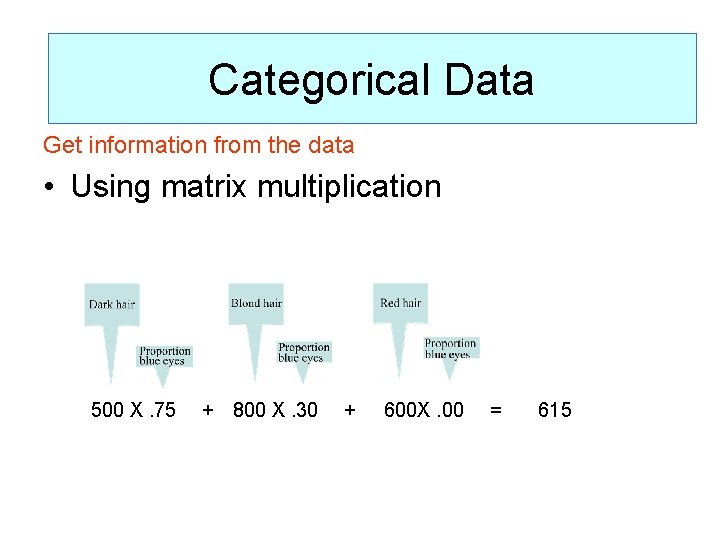
Categorical data Categorical (Goal: Organize the data/Get. Data information) Get information from the data • Using matrix multiplication 500 X. 75 + 800 X. 30 + 600 X. 00 = 615

Sample Data We sample the wine. (We don’t drink the whole bottle and then decide that the wine is no good. )

GOAL: Get Information from Data Get information about a population from a sample.

Sample Data • No information if the sample is not random Example: Samples of height Take sample from the basketball team Example: Proportion of male to female students Take sample from the girls dormitory • No information if the sample size is too small Example: A sample of one

Intuitive basis for inference from a sample Examples • Hypothesis: Equal number of male and female students A random sample of 30 students are all female Conclusion: Reject hypothesis • Hypothesis: A coin is fair The coin is tossed 20 times and results in 20 heads Conclusion: Reject hypothesis

Intuitive basis for inference from a sample Alternate examples • Hypothesis: Equal number of male and female students A random sample of 30 students, 21 are female Conclusion: Reject hypothesis? • Hypothesis: A coin is fair The coin is tossed 20 times, 16 heads Conclusion: Reject hypothesis?
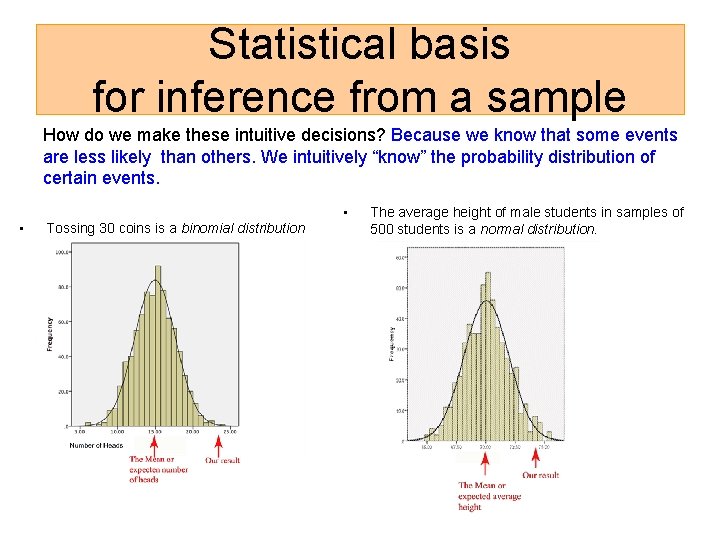
Statistical basis for inference from a sample How do we make these intuitive decisions? Because we know that some events are less likely than others. We intuitively “know” the probability distribution of certain events. • • Tossing 30 coins is a binomial distribution The average height of male students in samples of 500 students is a normal distribution.

Statistical basis for inference from a sample • For more refined estimates we need to know the probability distribution more accurately. Decision Rule: If the probability of getting the sample we actually got (or a more extreme sample) is very small (say. 05 or less), we reject our hypothesis.

Statistical basis for inference from a sample We use the calculator for graphing, for regression, for matrix operations, etc… So let’s use the calculator to find probabilities.

Statistical basis for inference from a sample Hypothesis: Proportion of females in population is 0. 6. Random sample of 100 has 70 females P-Value. 04 <. 05 Reject Hypothesis Random sample of 50 has 35 females P-Value. 14 >. 05 Fail to reject Hypothesis

Statistical basis for inference from a sample Hypothesis: Mean height of male students is 70”. Random sample of 20 has mean height 70. 13 P-Value. 69 >. 05 Fail to reject Hypothesis Random sample of 6 has mean height 72. 6 P-Value. 01 <. 05 Reject Hypothesis
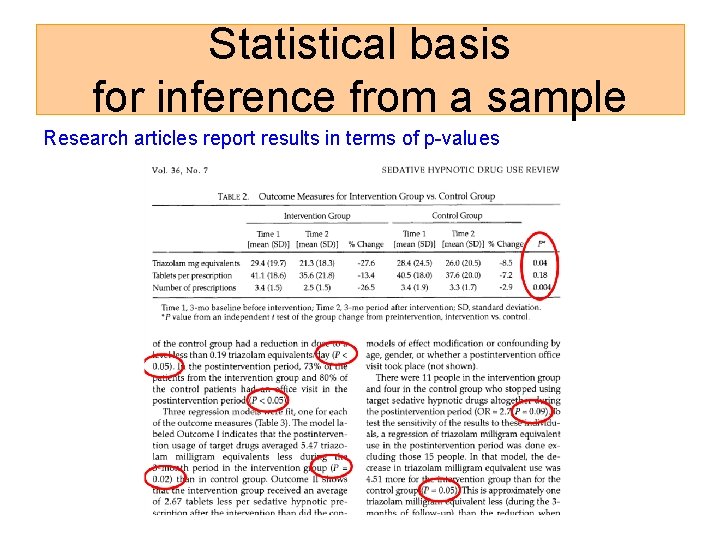
Statistical basis for inference from a sample Research articles report results in terms of p-values
- Slides: 54