Data Mining Speaker ChihYang Lin 1 Outline n

Data Mining Speaker: Chih-Yang Lin 1

Outline n Present two paper about clustering in Data Mining n n n Spatial Clustering Methods in Data Mining: A Survey Nonparametric Genetic Clustering: Comparison of Validity Some idea & future work 2

What is data mining n n n It can be considered as one of the steps in the Knowledge Discovery in Database(KDD) Commonly used to find the useful patterns or models It handles real world data that have large amount, dynamic, incomplete and noisy characteristics 3

The fields of data mining n n n n Mining association rules Data generalization and summarization Classification Clustering Pattern similarity Sequential Mining …………… 4

Spatial Clustering Methods in Data Mining: A Survey Author: Jiawei Han, M. Kamber and A. K. H. Tung Source: Geographic Data Mining and Knowledge Discovery 2001 5

Introduction Clustering in DM n n n Partition methods Hierarchical methods Density-based methods Grid-based methods Model-based methods 6

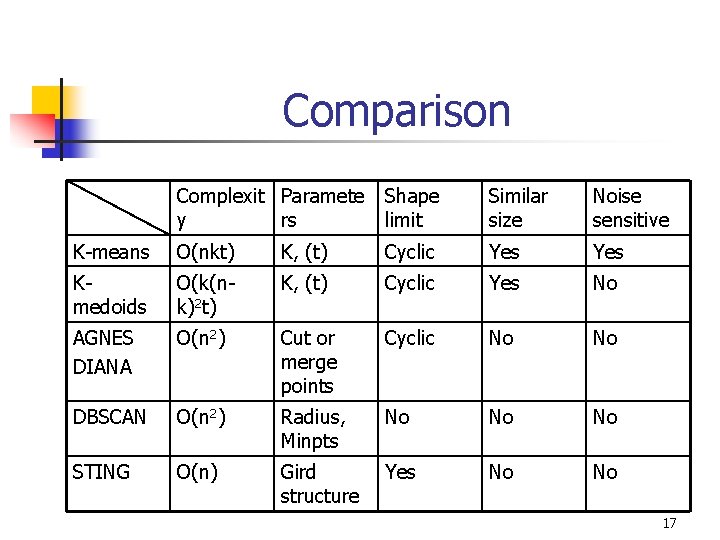
A good clustering method? n Parameter n n n # of clusters, # of neighbors, radius… Shape Similar size Noise sensitive Input order 7

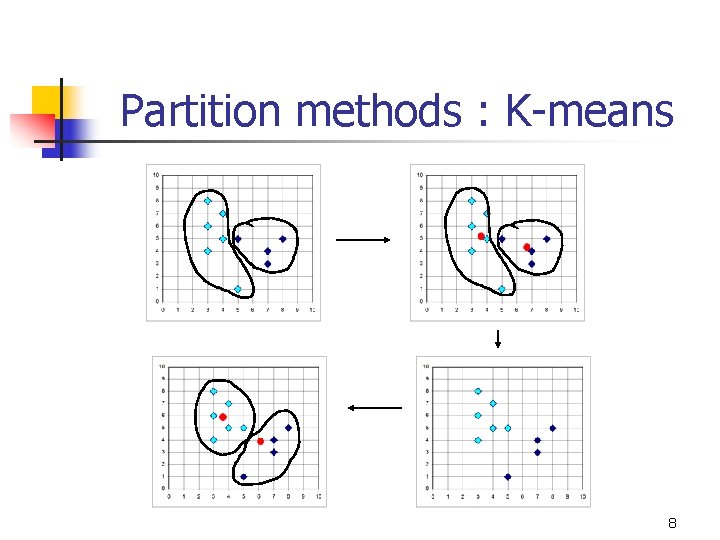
Partition methods : K-means 8

Partition methods : K-means n n n Time complexity: O(knt) Need to specify k in advance Unable to handle noisy and outliers Discover clusters with spherical shape Find global optimal centers or k clusters is NP-hard 9

Partition methods : K-medoid n n n Time complexity: O(k(n-k)2 t) Robust than k-means Other improved algorithms n CLARA(1990), CLARAN(Clustering Large Applications based upon Randomized Search)(1994) 10

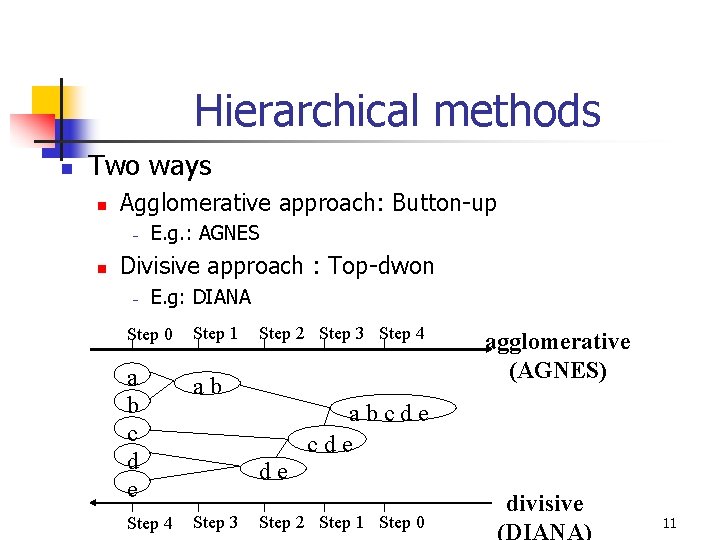
Hierarchical methods n Two ways n Agglomerative approach: Button-up – n E. g. : AGNES Divisive approach : Top-dwon – E. g: DIANA Step 0 Step 1 a b c d e ab Step 4 Step 3 Step 2 Step 3 Step 4 agglomerative (AGNES) abcde de Step 2 Step 1 Step 0 divisive (DIANA) 11

Hierarchical methods n n n Difficult to decide cut points or merge points Irreversible Time complexity: O(n 2) 12

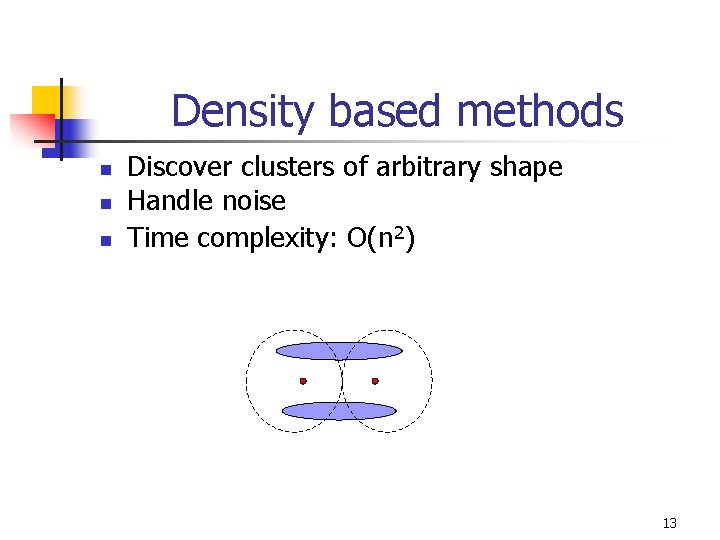
Density based methods n n n Discover clusters of arbitrary shape Handle noise Time complexity: O(n 2) 13

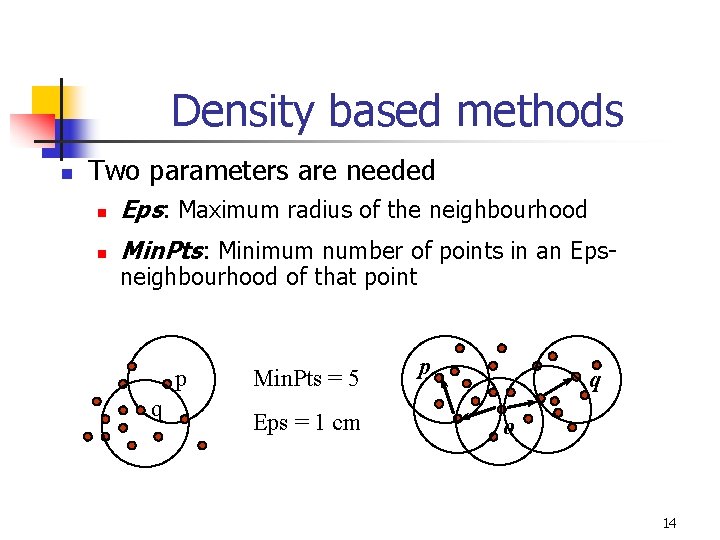
Density based methods n Two parameters are needed n Eps: Maximum radius of the neighbourhood n Min. Pts: Minimum number of points in an Epsneighbourhood of that point p q Min. Pts = 5 Eps = 1 cm p q o 14

Grid-Based Clustering Method n n Fast processing time, independent of the number of data objects, dependent on only the number of cells in each dimension Useful on high dimensional data 15

Model-Based Clustering methods n n Statistical approach Neural network approach 16

Comparison Complexit Paramete y rs Shape limit Similar size Noise sensitive K-means O(nkt) K, (t) Cyclic Yes Kmedoids O(k(nk)2 t) K, (t) Cyclic Yes No AGNES DIANA O(n 2) Cut or merge points Cyclic No No DBSCAN O(n 2) Radius, Minpts No No No STING O(n) Gird structure Yes No No 17

Nonparametric genetic clustering: comparison of validity indices Bandyopadhyay, S. ; Maulik, U. Machine IEEE Transactions on SMC, Part C: Applications and Reviews 2001 18

Introduction n n GA is a randomized and parallel searching algorithm GA operation n n Selection, crossover, mutation Develop a nonparametric clustering technique n Variable string length genetic algorithm (VGA) 19

VGA-Clustering(1) n n String representation : a chromosome means a kind of clustering result Chromosome i : n n Coordinates of centers of clusters (real number) Ki clusters, N dim. length = N*Ki center 1 (c 1, c 2 … c. N) n center 2 (c 1, c 2 … c. N) …… center Ki (c 1, c 2 … c. N) Partition : assigning the points to the closest cluster 20

VGA-Clustering (2) n Population initialization n Chromosome length: n n Ki = rand() mod K* (K*: upper bound of initial chromosome) Ki centers : randomly selected points from data set Selection: roulette wheel 21

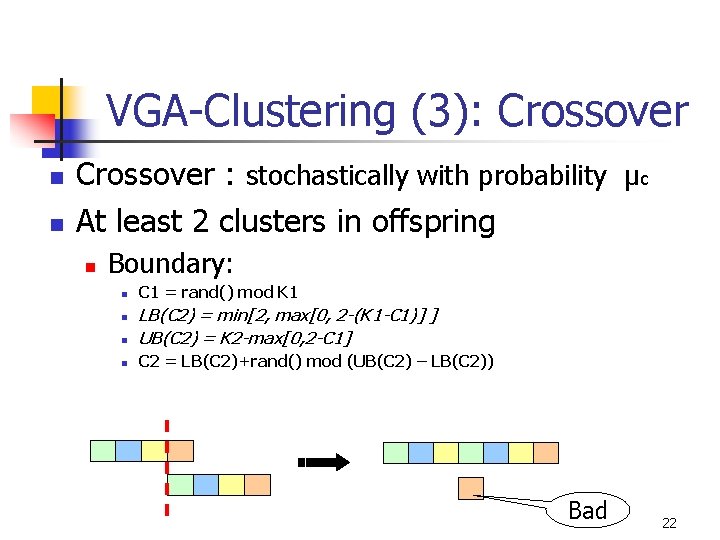
VGA-Clustering (3): Crossover n n Crossover : stochastically with probability μc At least 2 clusters in offspring n Boundary: n C 1 = rand() mod K 1 n LB(C 2) = min[2, max[0, 2 -(K 1 -C 1)] ] UB(C 2) = K 2 -max[0, 2 -C 1] n C 2 = LB(C 2)+rand() mod (UB(C 2) – LB(C 2)) n Bad 22

VGA-Clustering (4) n Mutation n probability μm Random d in [0, 1] Gene position v: (1 ± 2*d)*v , when v≠ 0 ± 2*d , v=0 23

Fitness Computation n Use the cluster validity indices n n DB Index Dunn’s Index Generalized Dunn’s Index νGD New Cluster Validity Index (by authors) 24

Cluster Validity Indices (1) n DB (Davies-Bouldin) Index §Within-cluster scatter : zi x x §Between-cluster separation : zi zj §ratio : §DB Index : (fitness : 1/DB) Ci : number of points in cluster i K : number of clusters Zi : centroid 25

Cluster Validity Indices (2) n Dunn’s Index: Let S, T be two nonempty subset §Diameter of S : y x §Set distance between S & T : S x y T §Dunn’s Index 26

Cluster Validity Indices (3) n Generalized Dunn’s Index n n δi: Any positive, semi-definite, symmetric set distance function Δi: Any positive, semi-definite, symmetric diameter function 27

Cluster Validity Indices (4) n New Cluster Validity Index §Scatter: zk x x §Separation : zi zj §Index: cluster number compact separation 28

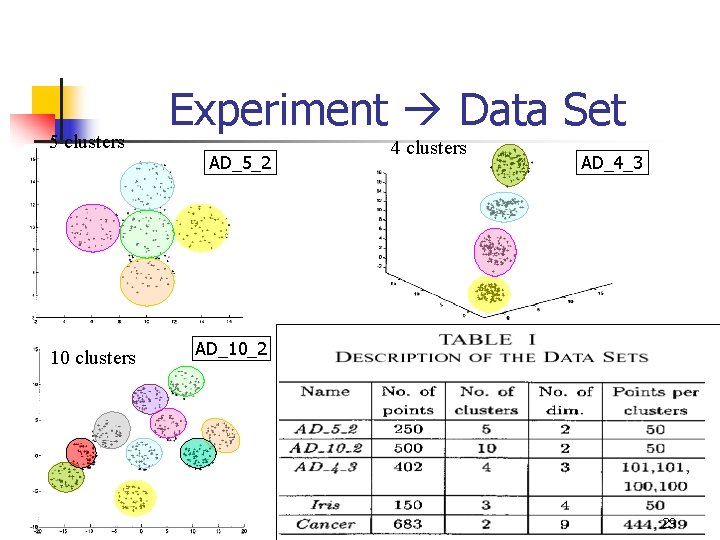
5 clusters 10 clusters Experiment Data Set AD_5_2 4 clusters AD_4_3 AD_10_2 29

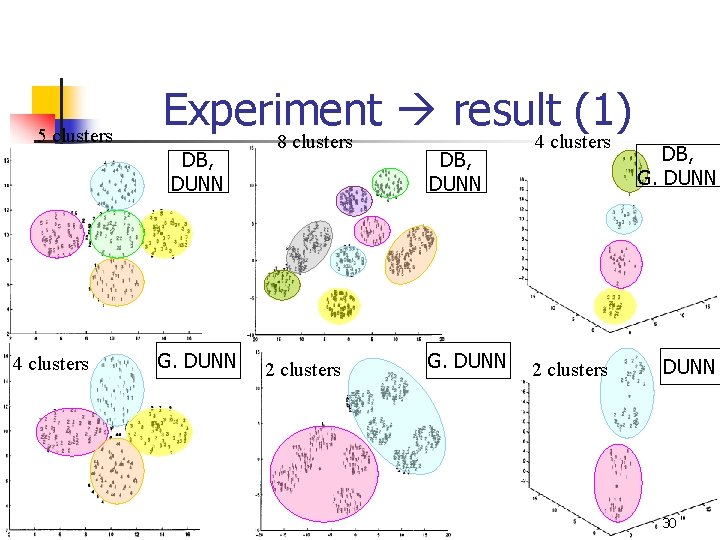
5 clusters Experiment result (1) DB, DUNN 4 clusters G. DUNN 8 clusters 2 clusters DB, DUNN G. DUNN 4 clusters 2 clusters DB, G. DUNN 30

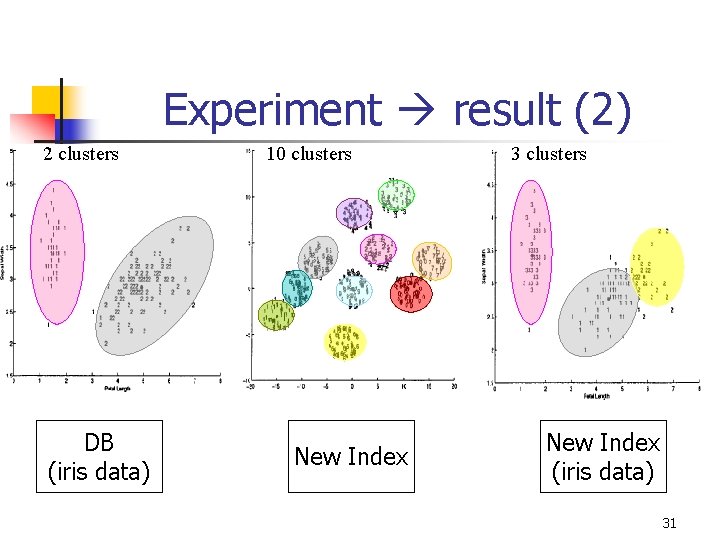
Experiment result (2) 2 clusters DB (iris data) 10 clusters New Index 3 clusters New Index (iris data) 31

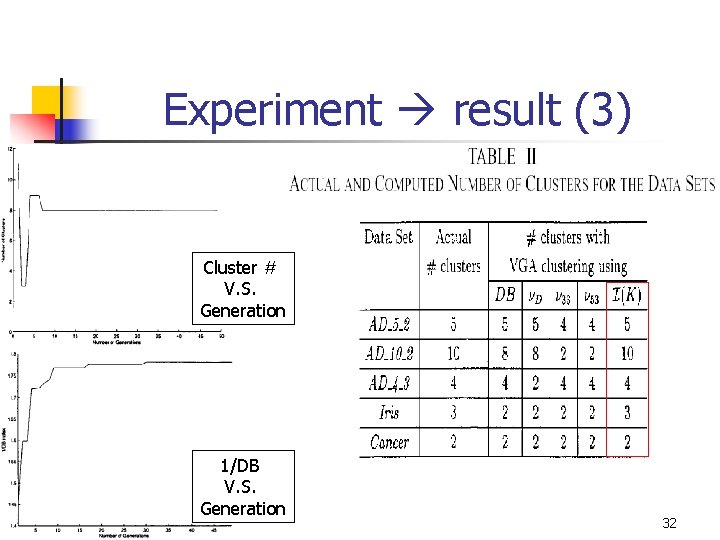
Experiment result (3) Cluster # V. S. Generation 1/DB V. S. Generation 32

Conclusion n n VGAs exploited for clustering when number of clusters is not known a priori New cluster validity index introduced n n Formation of compact and separated clusters. Provide correct number of clusters but other ones sometimes fail 33

Disadvantage n n n Handle only cyclic shape of clusters Similar size Chromosome encode too complex 34

Future work n bottleneck of apriori algorithms n n Specify parameter: support and confidence Too many IO costs Huge number of candidate sets Two efficient algorithms for association rules n n Hash based algorithm FP(frequent pattern)-tree 35

Future work n Bottleneck of parallel mining association rules n n n Communication overhead Load balancing Privacy and data security: encoding Bioinformatics Integrated clustering methods Incremental series 36

Bibliography n Journal n n n Special interest groups n n n Data Mining and Knowledge Discovery Journal IEEE trans. On Knowledge and Data Engineering (TKDE) ACM-SIGKDD ACM-SIGMOD Conference n n n IEEE International Conf. on Data Mining IEEE International Conf. On Data Engineering (ICDE) IEEE International Conf. On KDDM (KDD) SIAM International Conf. on Data Mining (SIAMDM) Pacific-Asia Conf. On KDDM (PAKDD) 37