Data Mining Classification Basic Concepts Decision Trees and

Data Mining Classification: Basic Concepts, Decision Trees, and Model Evaluation Lecture Notes for Chapter 4 Introduction to Data Mining by Tan, Steinbach, Kumar © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 1

Classification Errors l Training errors (apparent errors) – Errors committed on the training set l Test errors – Errors committed on the test set l Generalization errors – Expected error of a model over random selection of records from same distribution © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 2

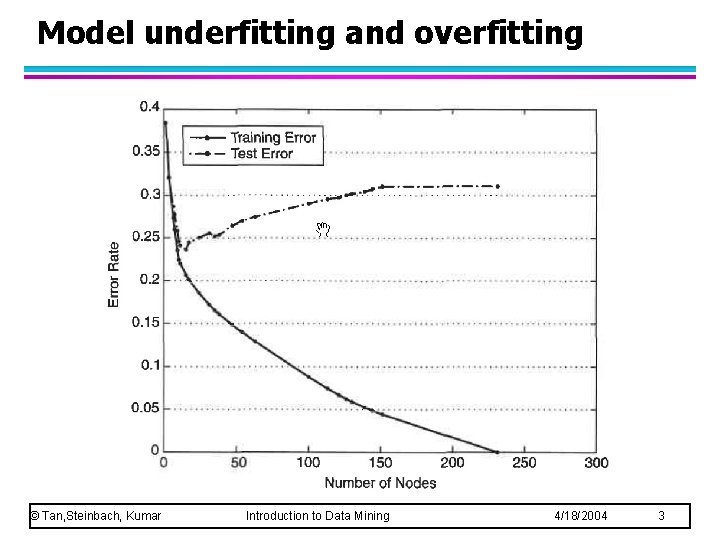
Model underfitting and overfitting © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 3

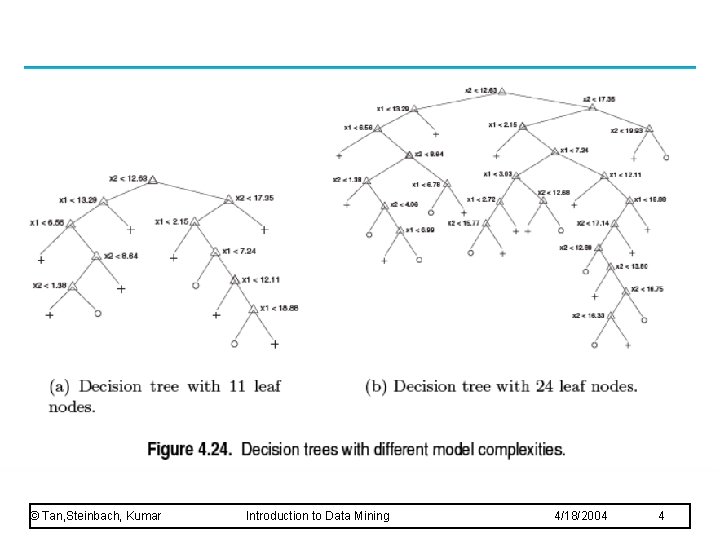
© Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 4

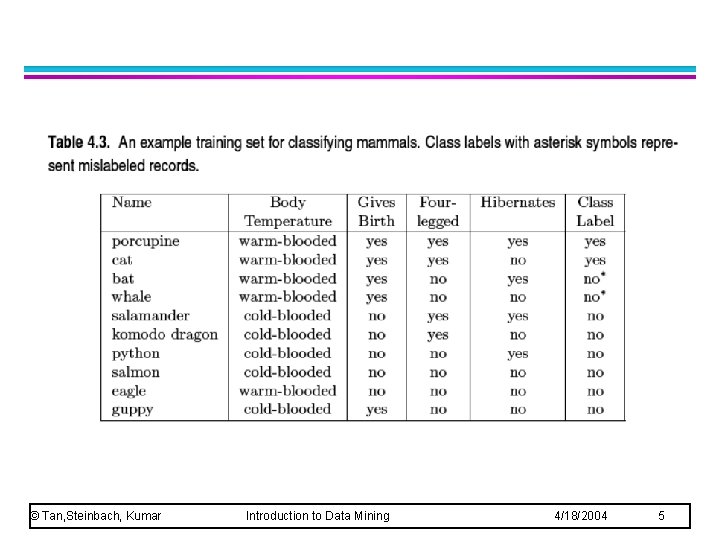
© Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 5

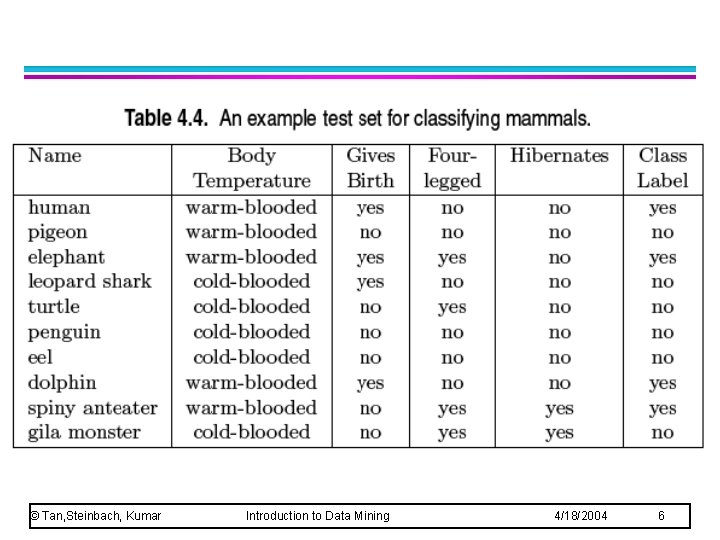
© Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 6

Training error rate = 0 Test error rate = 30% © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 8

Training error rate = 20% Test error rate = 10% © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 9

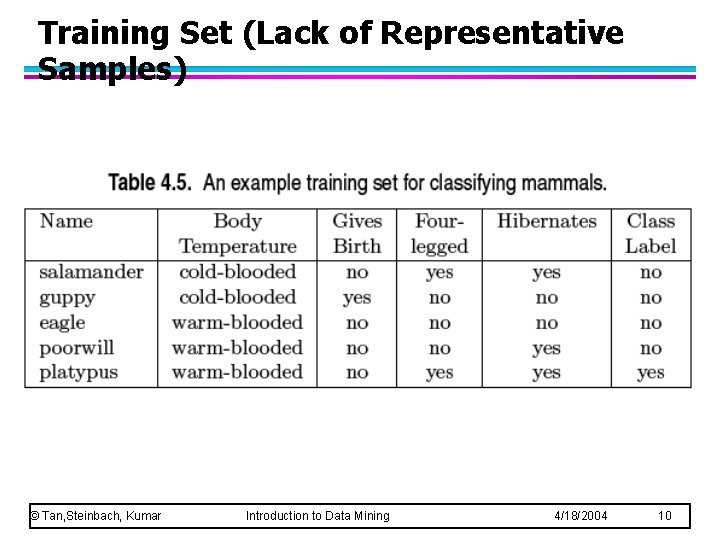
Training Set (Lack of Representative Samples) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 10

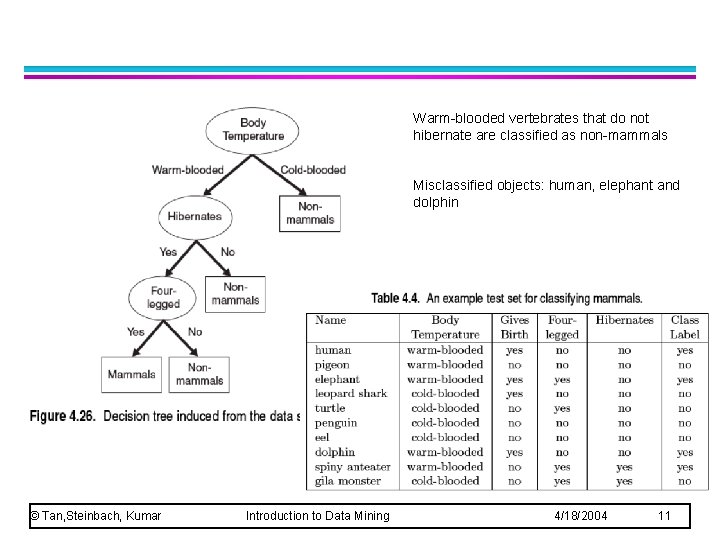
Warm-blooded vertebrates that do not hibernate are classified as non-mammals Misclassified objects: human, elephant and dolphin © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 11

Notes on Overfitting l Overfitting results in decision trees that are more complex than necessary l Training error (resubstitution) does not provide a good estimate of how well the tree will perform on previously unseen records l Need ways for estimating generalization errors © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 12

Estimating the Complexity of Decision Trees l Pessimistic Error Estimate of decision tree T with k leaf nodes: u : the number of training records classified by node t u : overall training error of the decisin tree uΩ( ): penalty term associated with each node u. Nt: the number of training records © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 13

Estimating the Complexity of Decision Trees: Example e(TL) = 4/24 e(TR) = 6/24 =1 egen(TL) = 4/24 + 1*7/24 = 11/24 = 0. 458 egen(TR) = 6/24 + 1*4/24 = 10/24 = 0. 417 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 14

Estimating the Complexity of Decision Trees l Resubstitution Estimate: – Using training error as an optimistic estimate of generalization error – Referred to as optimistic error estimate e(TL) = 4/24 e(TR) = 6/24 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 15

l Pre-Pruning (Early Stopping Rule) – Stop the algorithm before it becomes a fully-grown tree – Full stopping conditions for a node: u Stop if all instances belong to the same class u Stop if all the attribute values are the same – Early Stopping: u ? ? © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 16

l Pre-Pruning (Early Stopping Rule) – Stop the algorithm before it becomes a fully-grown tree – Full stopping conditions for a node: u Stop if all instances belong to the same class u Stop if all the attribute values are the same – Early Stopping: Stop if number of instances is less than some user-specified threshold u u Stop if expanding the current node does not improve impurity measures (e. g. , Gini or information gain). © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 17

l Pre-Pruning (Early Stopping Rule) – Stop the algorithm before it becomes a fully-grown tree – Full stopping conditions for a node: u Stop if all instances belong to the same class u Stop if all the attribute values are the same – Early Stopping: Stop if number of instances is less than some user-specified threshold u u Stop if expanding the current node does not improve impurity measures (e. g. , Gini or information gain). – Advantage and disadvantage: u ? ? © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 18

l Pre-Pruning (Early Stopping Rule) – Early Stopping: Stop if number of instances is less than some user-specified threshold u u Stop if expanding the current node does not improve impurity measures (e. g. , Gini or information gain). – Advantage: u Avoid generating overly complex subtrees. – Disadvantage: u It is difficult to choose the right threshold. Subsequent splitting may result in better subtrees even if no significant gain is obtained in current node. u © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 19

How to Address Overfitting… l Post-pruning – Grow decision tree to its entirety – Trim the nodes of the decision tree in a bottom -up fashion – How? ? ? © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 20

How to Address Overfitting… l Post-pruning – Grow decision tree to its entirety – Trim the nodes of the decision tree in a bottom -up fashion – Replace sub-tree by a leaf node or replace subtree by the most frequently used branch of the subtree. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 21

How to Address Overfitting… Post-pruning – Grow decision tree to its entirety – Trim the nodes of the decision tree in a bottom -up fashion – Replace sub-tree by a leaf node or replace subtree by the most frequently used branch of the subtree. l Advantage – ? ? ? l Disadvantage – ? ? ? l © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 22

How to Address Overfitting… Post-pruning – Grow decision tree to its entirety – Trim the nodes of the decision tree in a bottom -up fashion – Replace sub-tree by a leaf node or replace subtree by the most frequently used branch of the subtree. l Advantage – Give better result. l Disadvantage – May waste additional computations l © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 23

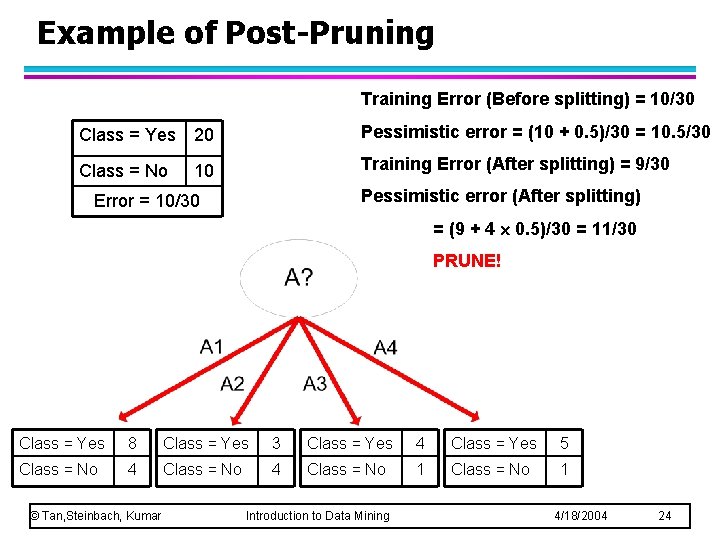
Example of Post-Pruning Training Error (Before splitting) = 10/30 Class = Yes 20 Pessimistic error = (10 + 0. 5)/30 = 10. 5/30 Class = No 10 Training Error (After splitting) = 9/30 Pessimistic error (After splitting) Error = 10/30 = (9 + 4 0. 5)/30 = 11/30 PRUNE! Class = Yes 8 Class = Yes 3 Class = Yes 4 Class = Yes 5 Class = No 4 Class = No 1 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 24