Data Mining Classification Basic Concepts Decision Trees and

Data Mining Classification: Basic Concepts, Decision Trees, and Model Evaluation Lecture Notes for Chapter 4 Introduction to Data Mining By Tan, Steinbach, Kumar Lecture 3 Basic Classification © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 1

Classification: Definition l Given a collection of records (training set ) – Each record contains a set of attributes, one of the attributes is the class. l l Find a model for class attribute as a function of the values of other attributes. Goal: previously unseen records should be assigned a class as accurately as possible. – A test set is used to determine the accuracy of the model. Usually, the given data set is divided into training and test sets, with training set used to build the model and test set used to validate it. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 2

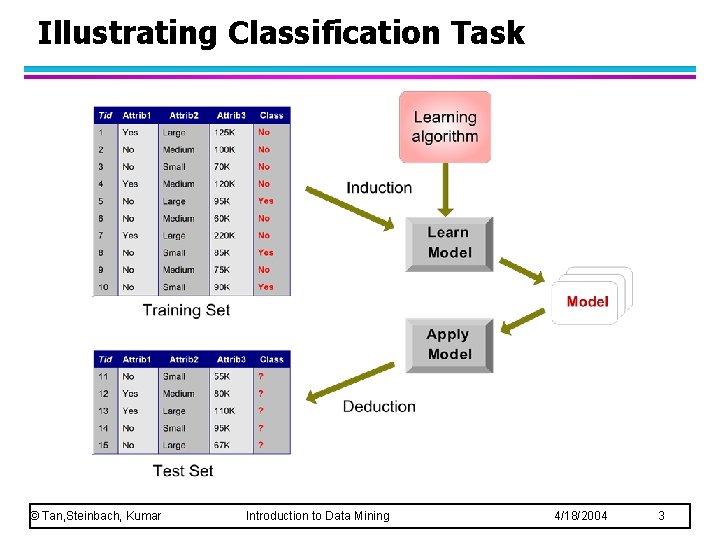
Illustrating Classification Task © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 3

Examples of Classification Task l Predicting tumor cells as benign or malignant l Classifying credit card transactions as legitimate or fraudulent l Classifying secondary structures of protein as alpha-helix, beta-sheet, or random coil l Categorizing news stories as finance, weather, entertainment, sports, etc © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 4

Classification Techniques Decision Tree based Methods l Rule-based Methods l Memory based reasoning l Neural Networks l Naïve Bayes and Bayesian Belief Networks l Support Vector Machines l © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 5

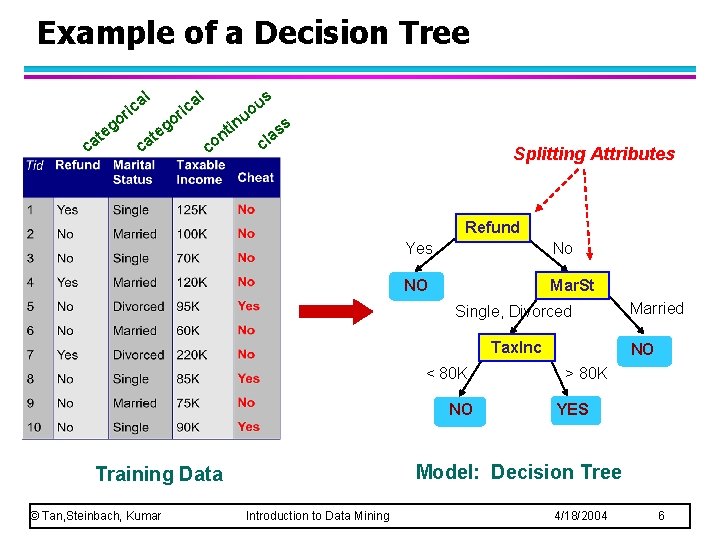
Example of a Decision Tree al ric at c o eg c at al o eg ric in nt co s u o u ss a cl Splitting Attributes Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO NO > 80 K YES Model: Decision Tree Training Data © Tan, Steinbach, Kumar Married Introduction to Data Mining 4/18/2004 6

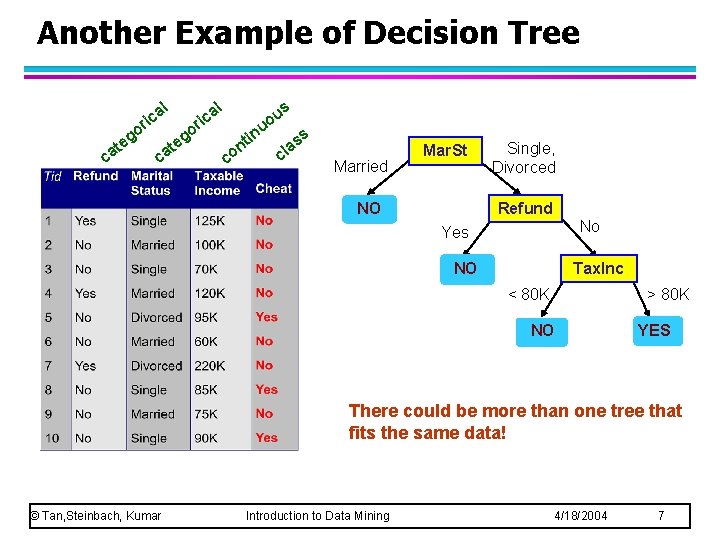
Another Example of Decision Tree l g te ca l a ric o o ca g te s a ric u uo co in t n ss a cl Married Mar. St NO Single, Divorced Refund No Yes NO Tax. Inc < 80 K > 80 K NO YES There could be more than one tree that fits the same data! © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 7

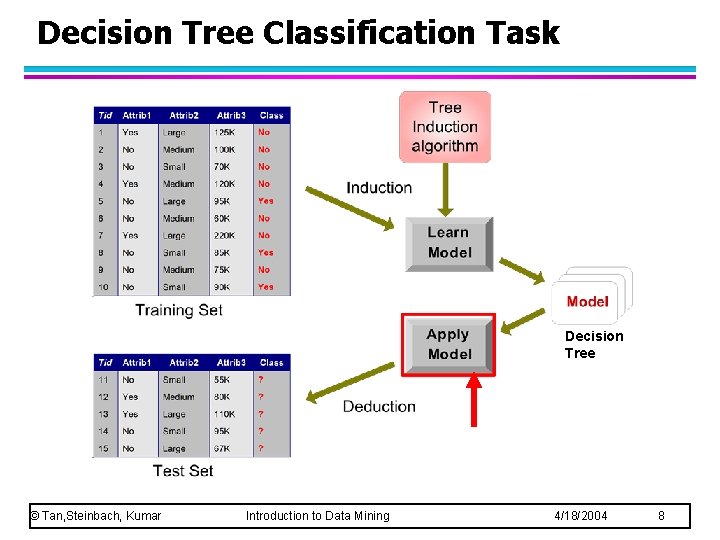
Decision Tree Classification Task Decision Tree © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 8

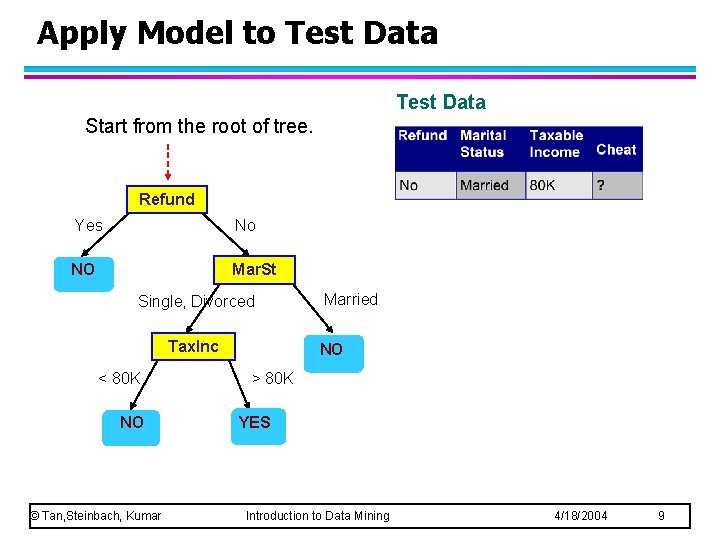
Apply Model to Test Data Start from the root of tree. Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married NO > 80 K YES Introduction to Data Mining 4/18/2004 9

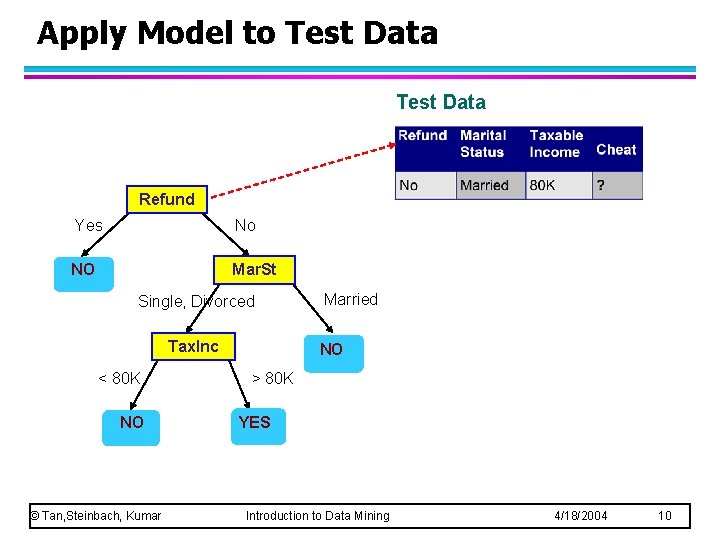
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married NO > 80 K YES Introduction to Data Mining 4/18/2004 10

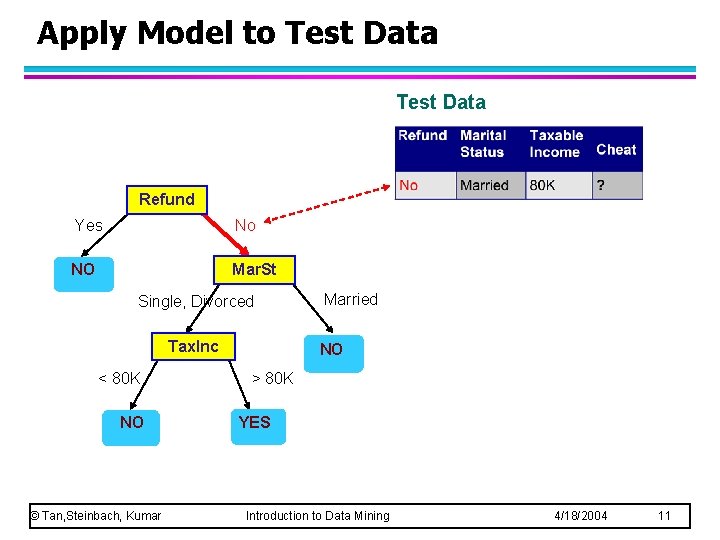
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married NO > 80 K YES Introduction to Data Mining 4/18/2004 11

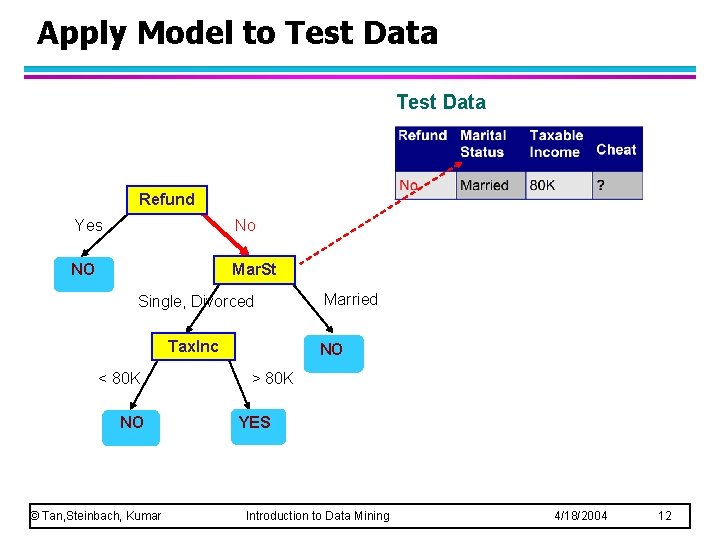
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married NO > 80 K YES Introduction to Data Mining 4/18/2004 12

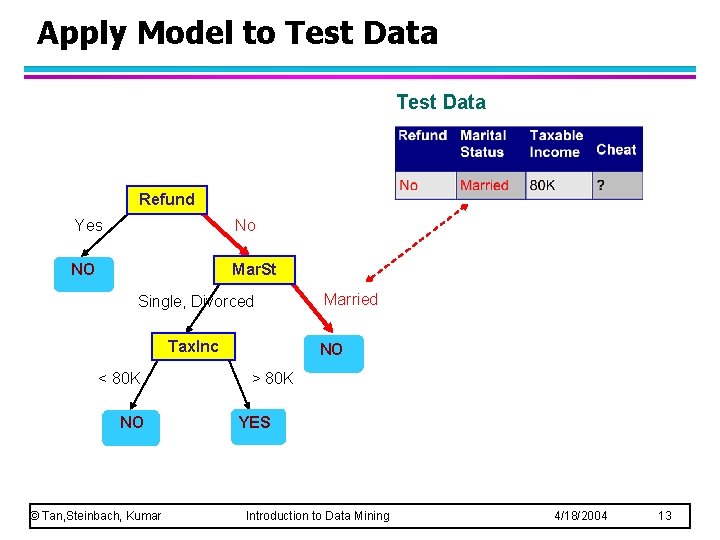
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married NO > 80 K YES Introduction to Data Mining 4/18/2004 13

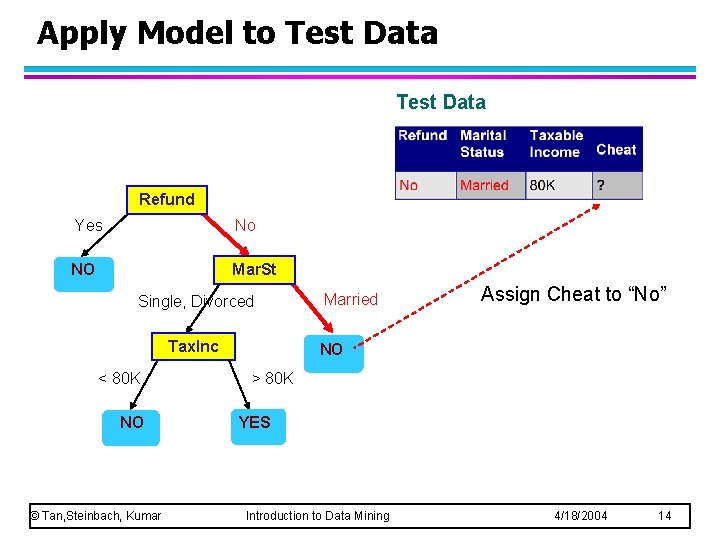
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO © Tan, Steinbach, Kumar Married Assign Cheat to “No” NO > 80 K YES Introduction to Data Mining 4/18/2004 14

Decision Tree Classification Task Decision Tree © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 15

Decision Tree Induction l Many Algorithms: – Hunt’s Algorithm (one of the earliest) – CART – ID 3, C 4. 5 – SLIQ, SPRINT © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 16

General Structure of Hunt’s Algorithm l l Let Dt be the set of training records that reach a node t General Procedure: – If Dt contains records that belong the same class yt, then t is a leaf node labeled as yt – If Dt is an empty set, then t is a leaf node labeled by the default class, yd – If Dt contains records that belong to more than one class, use an attribute test to split the data into smaller subsets. Recursively apply the procedure to each subset. © Tan, Steinbach, Kumar Introduction to Data Mining Dt ? 4/18/2004 17

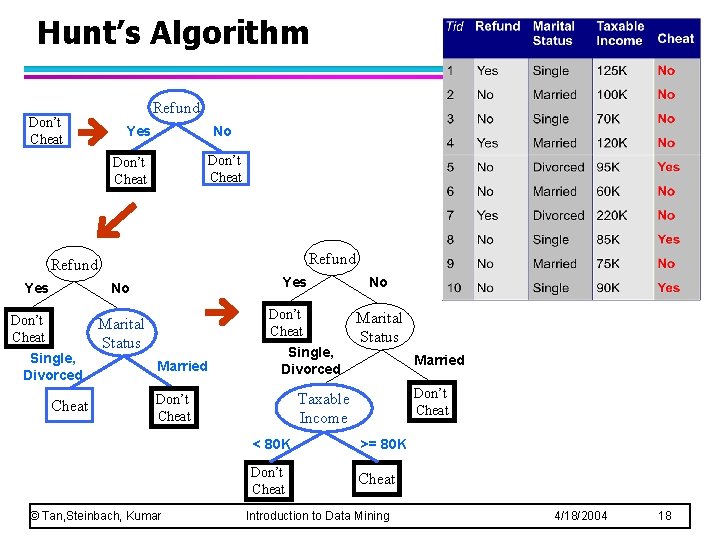
Hunt’s Algorithm Don’t Cheat Refund Yes No Don’t Cheat Single, Divorced Cheat Don’t Cheat Marital Status Married Single, Divorced Marital Status Married Don’t Cheat Taxable Income Don’t Cheat © Tan, Steinbach, Kumar No < 80 K >= 80 K Don’t Cheat Introduction to Data Mining 4/18/2004 18

Tree Induction l Greedy strategy. – Split the records based on an attribute test that optimizes certain criterion. l Issues – Determine how to split the records u. How to specify the attribute test condition? u. How to determine the best split? – Determine when to stop splitting © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 19

Tree Induction l Greedy strategy. – Split the records based on an attribute test that optimizes certain criterion. l Issues – Determine how to split the records u. How to specify the attribute test condition? u. How to determine the best split? – Determine when to stop splitting © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 20

How to Specify Test Condition? l Depends on attribute types – Nominal – Ordinal – Continuous l Depends on number of ways to split – 2 -way split – Multi-way split © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 21

Splitting Based on Nominal Attributes l Multi-way split: Use as many partitions as distinct values. Car. Type Family Luxury Sports l Binary split: Divides values into two subsets. Need to find optimal partitioning. {Sports, Luxury} Car. Type © Tan, Steinbach, Kumar {Family} OR Introduction to Data Mining {Family, Luxury} Car. Type {Sports} 4/18/2004 22

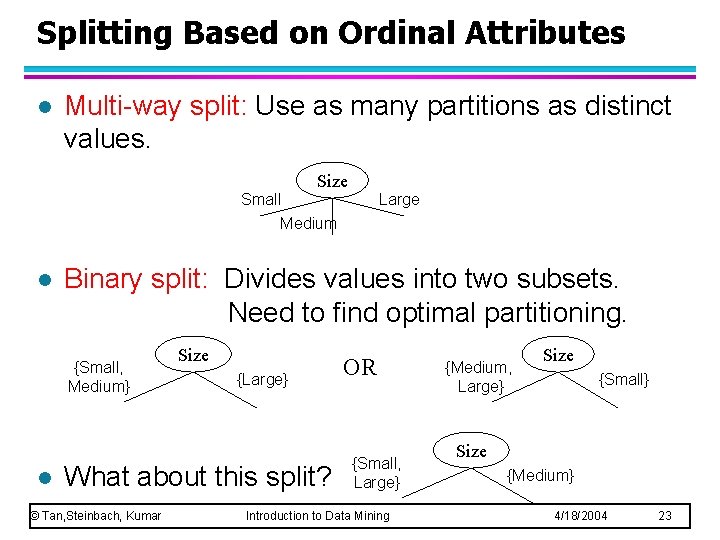
Splitting Based on Ordinal Attributes l Multi-way split: Use as many partitions as distinct values. Size Small Medium l Binary split: Divides values into two subsets. Need to find optimal partitioning. {Small, Medium} l Large Size {Large} What about this split? © Tan, Steinbach, Kumar OR {Small, Large} Introduction to Data Mining {Medium, Large} Size {Small} Size {Medium} 4/18/2004 23

Splitting Based on Continuous Attributes l Different ways of handling – Discretization to form an ordinal categorical attribute Static – discretize once at the beginning u Dynamic – ranges can be found by equal interval bucketing, equal frequency bucketing (percentiles), or clustering. u – Binary Decision: (A < v) or (A v) consider all possible splits and finds the best cut u can be more compute intensive u © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 24

Splitting Based on Continuous Attributes © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 25

Tree Induction l Greedy strategy. – Split the records based on an attribute test that optimizes certain criterion. l Issues – Determine how to split the records u. How to specify the attribute test condition? u. How to determine the best split? – Determine when to stop splitting © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 26

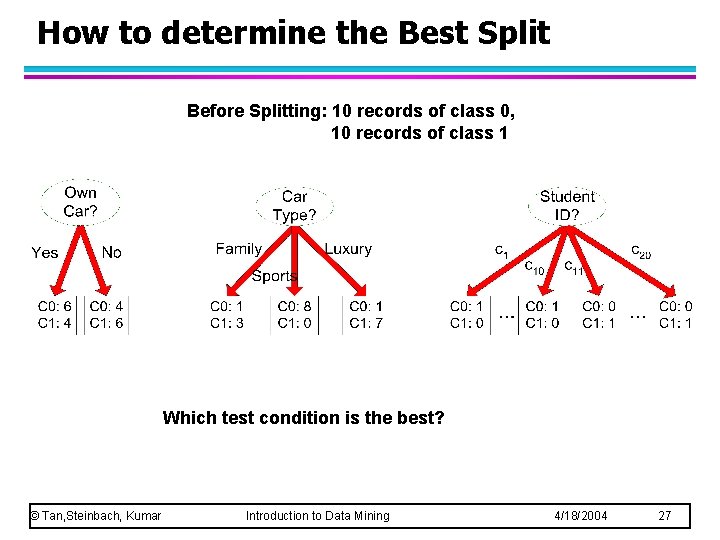
How to determine the Best Split Before Splitting: 10 records of class 0, 10 records of class 1 Which test condition is the best? © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 27

How to determine the Best Split Greedy approach: – Nodes with homogeneous class distribution are preferred l Need a measure of node impurity: l Non-homogeneous, High degree of impurity Low degree of impurity © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 28

Measures of Node Impurity l Gini Index l Entropy l Misclassification error © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 29

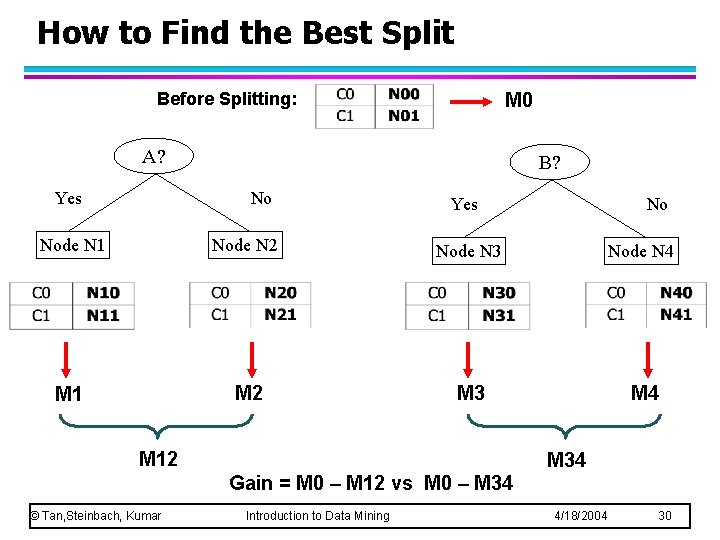
How to Find the Best Split Before Splitting: M 0 A? Yes B? No Yes No Node N 1 Node N 2 Node N 3 Node N 4 M 1 M 2 M 3 M 4 M 12 M 34 Gain = M 0 – M 12 vs M 0 – M 34 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 30

Measure of Impurity: GINI l Gini Index for a given node t : (NOTE: p( j | t) is the relative frequency of class j at node t). – Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information – Minimum (0. 0) when all records belong to one class, implying most interesting information © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 31

Examples for computing GINI P(C 1) = 0/6 = 0 P(C 2) = 6/6 = 1 Gini = 1 – P(C 1)2 – P(C 2)2 = 1 – 0 – 1 = 0 P(C 1) = 1/6 P(C 2) = 5/6 Gini = 1 – (1/6)2 – (5/6)2 = 0. 278 P(C 1) = 2/6 P(C 2) = 4/6 Gini = 1 – (2/6)2 – (4/6)2 = 0. 444 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 32

Splitting Based on GINI l l Used in CART, SLIQ, SPRINT. When a node p is split into k partitions (children), the quality of split is computed as, where, © Tan, Steinbach, Kumar ni = number of records at child i, n = number of records at node p. Introduction to Data Mining 4/18/2004 33

Binary Attributes: Computing GINI Index l l Splits into two partitions Effect of Weighing partitions: – Larger and Purer Partitions are sought for. B? Yes Gini(N 1) = 1 – (5/7)2 – (2/7)2 = 0. 4082 Node N 1 No Node N 2 Gini(Children) = 7/12 * 0. 4082 + 5/12 * 0. 32 = 0. 3715 Gini(N 2) = 1 – (1/5)2 – (4/5)2 = 0. 32 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 34

Categorical Attributes: Computing Gini Index l l For each distinct value, gather counts for each class in the dataset Use the count matrix to make decisions Multi-way split © Tan, Steinbach, Kumar Two-way split (find best partition of values) Introduction to Data Mining 4/18/2004 35

Continuous Attributes: Computing Gini Index l l Use Binary Decisions based on one value Several Choices for the splitting value – Number of possible splitting values = Number of distinct values Each splitting value has a count matrix associated with it – Class counts in each of the partitions, A < v and A v Simple method to choose best v – For each v, scan the database to gather count matrix and compute its Gini index – Computationally Inefficient! Repetition of work. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 36

Continuous Attributes: Computing Gini Index. . . l For efficient computation: for each attribute, – Sort the attribute on values – Linearly scan these values, each time updating the count matrix and computing gini index – Choose the split position that has the least gini index Sorted Values Split Positions © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 37

Alternative Splitting Criteria based on INFO l Entropy at a given node t: (NOTE: p( j | t) is the relative frequency of class j at node t). – Measures homogeneity of a node. u Maximum (log nc) when records are equally distributed among all classes implying least information u Minimum (0. 0) when all records belong to one class, implying most information – Entropy based computations are similar to the GINI index computations © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 38

Examples for computing Entropy P(C 1) = 0/6 = 0 P(C 2) = 6/6 = 1 Entropy = – 0 log 0 – 1 log 1 = – 0 = 0 P(C 1) = 1/6 P(C 2) = 5/6 Entropy = – (1/6) log 2 (1/6) – (5/6) log 2 (5/6) = 0. 65 P(C 1) = 2/6 P(C 2) = 4/6 Entropy = – (2/6) log 2 (2/6) – (4/6) log 2 (4/6) = 0. 92 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 39

Splitting Based on INFO. . . l Information Gain: Parent Node, p is split into k partitions; ni is number of records in partition i – Measures Reduction in Entropy achieved because of the split. Choose the split that achieves most reduction (maximizes GAIN) – Used in ID 3 and C 4. 5 – Disadvantage: Tends to prefer splits that result in large number of partitions, each being small but pure. © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 40

Splitting Based on INFO. . . l Gain Ratio: Parent Node, p is split into k partitions ni is the number of records in partition i – Adjusts Information Gain by the entropy of the partitioning (Split. INFO). Higher entropy partitioning (large number of small partitions) is penalized! – Used in C 4. 5 – Designed to overcome the disadvantage of Information Gain © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 41

Splitting Criteria based on Classification Error l Classification error at a node t : l Measures misclassification error made by a node. u Maximum (1 - 1/nc) when records are equally distributed among all classes, implying least interesting information u Minimum (0. 0) when all records belong to one class, implying most interesting information © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 42

Examples for Computing Error P(C 1) = 0/6 = 0 P(C 2) = 6/6 = 1 Error = 1 – max (0, 1) = 1 – 1 = 0 P(C 1) = 1/6 P(C 2) = 5/6 Error = 1 – max (1/6, 5/6) = 1 – 5/6 = 1/6 P(C 1) = 2/6 P(C 2) = 4/6 Error = 1 – max (2/6, 4/6) = 1 – 4/6 = 1/3 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 43

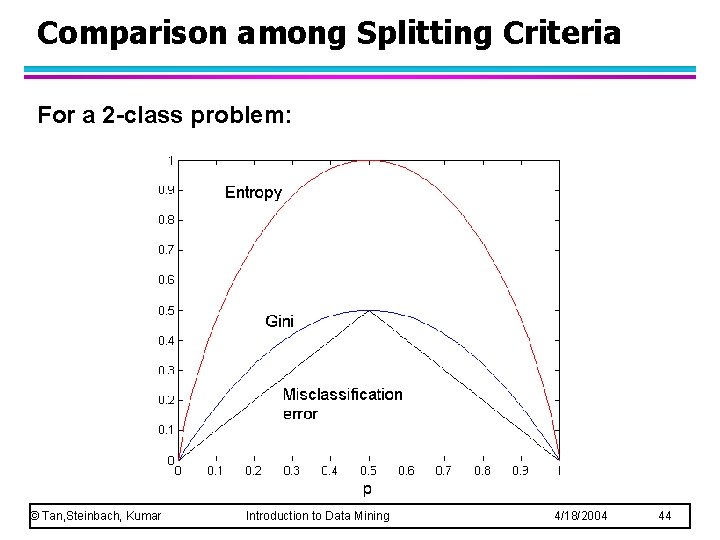
Comparison among Splitting Criteria For a 2 -class problem: © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 44

Misclassification Error vs Gini A? Yes Node N 1 No Node N 2 Error(N 1) = 1 – max[(3/3), (0/3)] =1 -1=0 Error(Children) = 3/10 * 0 + 7/10 * [3/7] = 0. 3 Error(N 2) = 1 – max[(4/7), (3/7)] = 1 – 4/7 = 3/7 © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 45

Misclassification Error vs Gini A? Yes Node N 1 No Node N 2 Gini(N 1) = 1 – (3/3)2 – (0/3)2 =0 Gini(Children) = 3/10 * 0 + 7/10 * 0. 489 = 0. 342 Gini(N 2) = 1 – (4/7)2 – (3/7)2 = 0. 489 © Tan, Steinbach, Kumar Gini improves Introduction to Data Mining 4/18/2004 46

Tree Induction l Greedy strategy. – Split the records based on an attribute test that optimizes certain criterion. l Issues – Determine how to split the records u. How to specify the attribute test condition? u. How to determine the best split? – Determine when to stop splitting © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 47

Stopping Criteria for Tree Induction l Stop expanding a node when all the records belong to the same class l Stop expanding a node when all the records have similar attribute values l Early termination (to be discussed later) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 48

Decision Tree Based Classification l Advantages: – Inexpensive to construct – Extremely fast at classifying unknown records – Easy to interpret for small-sized trees – Accuracy is comparable to other classification techniques for many simple data sets © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 49

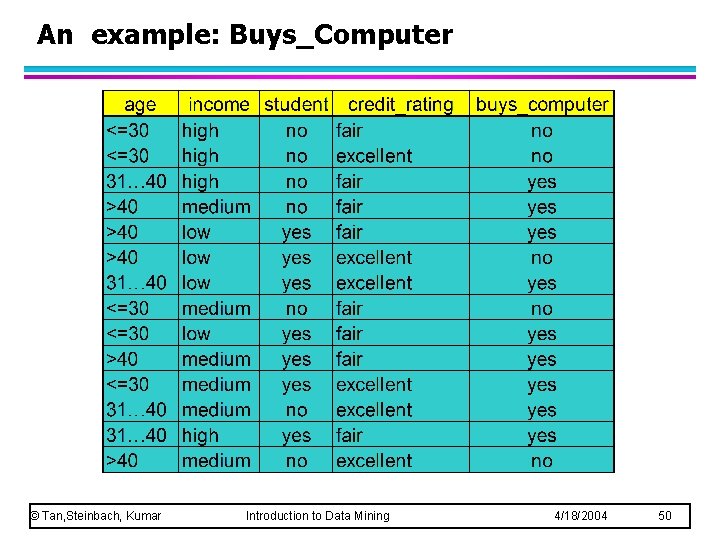
An example: Buys_Computer © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 50

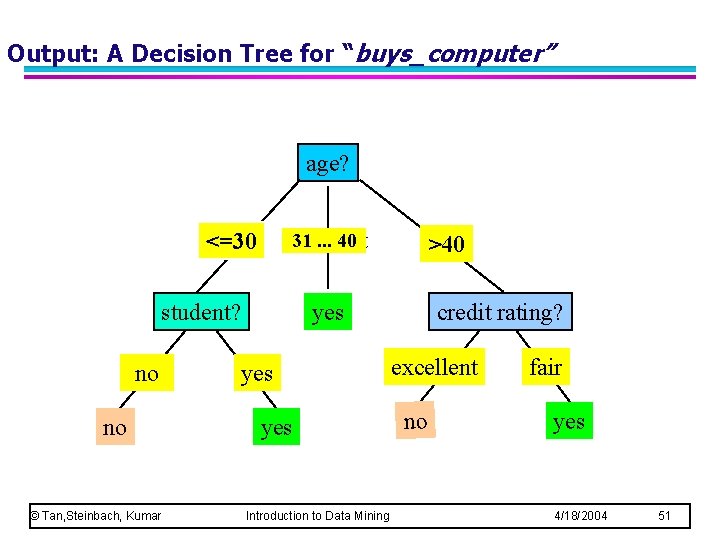
Output: A Decision Tree for “buys_computer” age? 31. . . 40 overcast <=30 student? no no © Tan, Steinbach, Kumar >40 credit rating? yes yes Introduction to Data Mining excellent no fair yes 4/18/2004 51

Attribute Selection Measure: Information Gain (ID 3/C 4. 5) n n n Select the attribute with the highest information gain Let pi be the probability that an arbitrary tuple in D belongs to class Ci, estimated by |Ci, D|/|D| Expected information (entropy) needed to classify a tuple in D: Information needed (after using A to split D into v partitions) to classify D: Information gained by branching on attribute A © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 52

Attribute Selection: Information Gain g Class P: buys_computer = “yes” g Class N: buys_computer = “no” means “age <=30” has 5 out of 14 samples, with 2 yes’es and 3 no’s. Hence Similarly, © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 53

Computing Information-Gain for Continuous-Value Attributes l Let attribute A be a continuous-valued attribute l Must determine the best split point for A – Sort the value A in increasing order – Typically, the midpoint between each pair of adjacent values is considered as a possible split point u(ai+ai+1)/2 is the midpoint between the values of ai and ai+1 – The point with the minimum expected information requirement for A is selected as the split-point for A l Split: – D 1 is the set of tuples in D satisfying A ≤ split-point, and D 2 is the set of tuples in D satisfying A > split-point © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 54

Gain Ratio for Attribute Selection (C 4. 5) l Information gain measure is biased towards attributes with a large number of values l C 4. 5 (a successor of ID 3) uses gain ratio to overcome the problem (normalization to information gain) – Gain. Ratio(A) = Gain(A)/Split. Info(A) l Ex. – gain_ratio(income) = 0. 029/0. 926 = 0. 031 l The attribute with the maximum gain ratio is selected as the splitting attribute © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 55

Gini index (CART, IBM Intelligent. Miner) l If a data set D contains examples from n classes, gini index, gini(D) is defined as where pj is the relative frequency of class j in D l If a data set D is split on A into two subsets D 1 and D 2, the gini index gini(D) is defined as l Reduction in Impurity: l The attribute provides the smallest ginisplit(D) (or the largest reduction in impurity) is chosen to split the node (need to enumerate all the possible splitting points for each attribute) © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 56

Decision Tree Induction by C 4. 5 Simple depth-first construction. l Uses Information Gain l Sorts Continuous Attributes at each node. l Needs entire data to fit in memory. l Unsuitable for Large Datasets. – Needs out-of-core sorting. l l You can download the software from: http: //www. cse. unsw. edu. au/~quinlan/c 4. 5 r 8. tar. gz © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 57