Data Mining Classification and Clustering Techniques Introduction to

Data Mining Classification and Clustering Techniques Introduction to Data Mining by Tan, Steinbach, Kumar Thank you very much for all materials © Tan, Steinbach, Kumar Introduction to Data Mining 4/18/2004 1

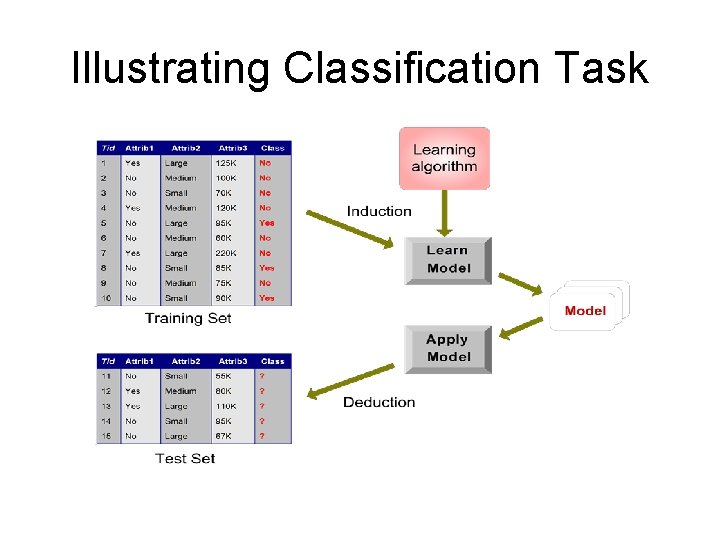
Classification: Definition • Given a collection of records (training set ) – Each record contains a set of attributes, one of the attributes is the class. • Find a model for class attribute as a function of the values of other attributes. • Goal: previously unseen records should be assigned a class as accurately as possible. – A test set is used to determine the accuracy of the model. Usually, the given data set is divided into training and test sets, with training set used to build the model and test set used to validate it.

Illustrating Classification Task

Examples of Classification Task • Predicting tumor cells as benign or malignant • Classifying credit card transactions as legitimate or fraudulent • Classifying secondary structures of protein as alpha-helix, beta-sheet, or random coil • Categorizing news stories as finance, weather, entertainment, sports, etc

Classification Techniques • • • Decision Tree based Methods Rule-based Methods Memory based reasoning Neural Networks Naïve Bayes and Bayesian Belief Networks • Support Vector Machines

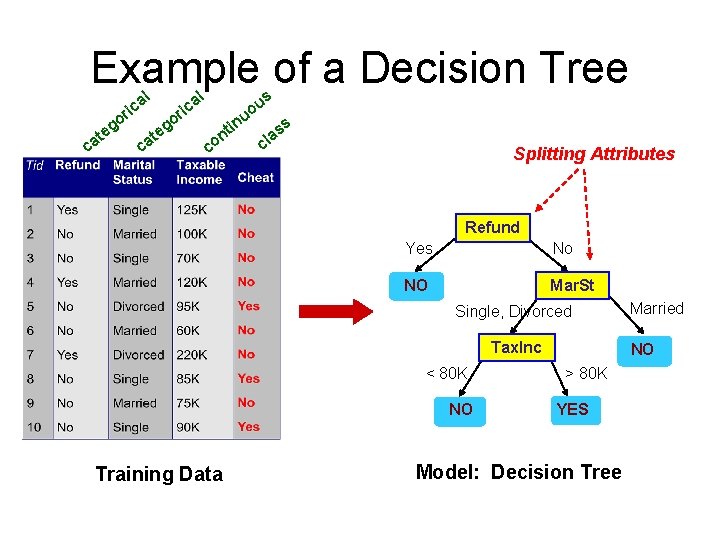
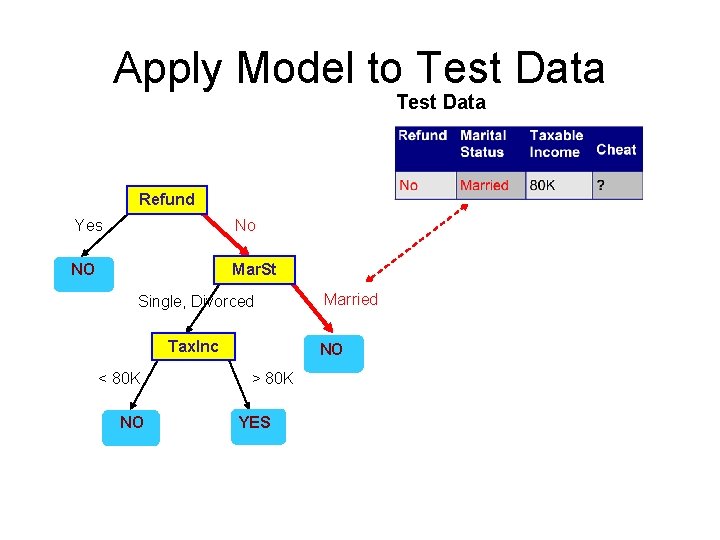
Example of a Decision Tree al ric c at o eg c at al o eg ric in nt co u s u o ss a cl Splitting Attributes Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Training Data Married NO > 80 K YES Model: Decision Tree

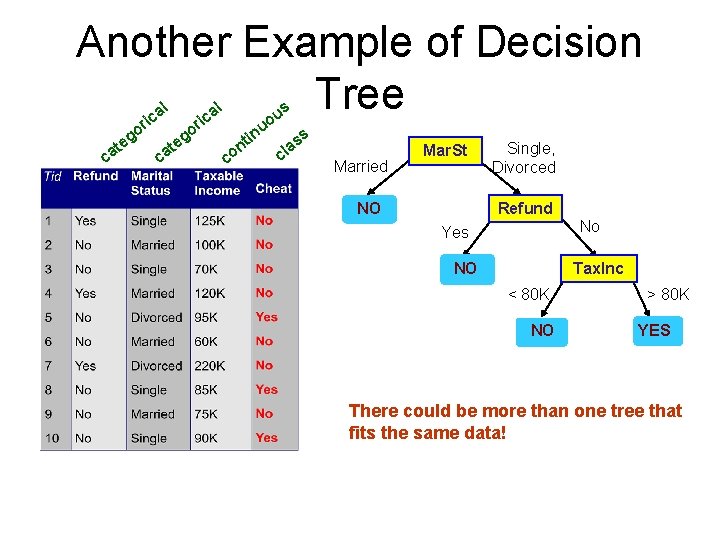
Another Example of Decision Tree l ca g te l a ric o o ca g te s a ric u uo co in t n ss a cl Married Mar. St NO Single, Divorced Refund No Yes NO Tax. Inc < 80 K NO > 80 K YES There could be more than one tree that fits the same data!

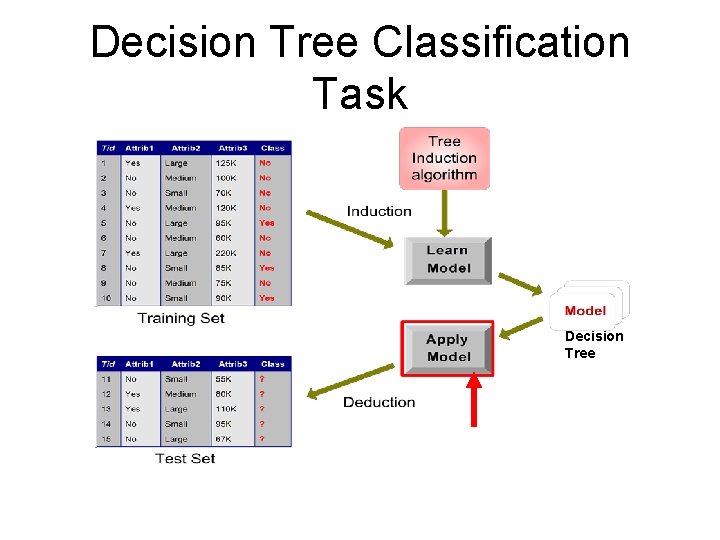
Decision Tree Classification Task Decision Tree

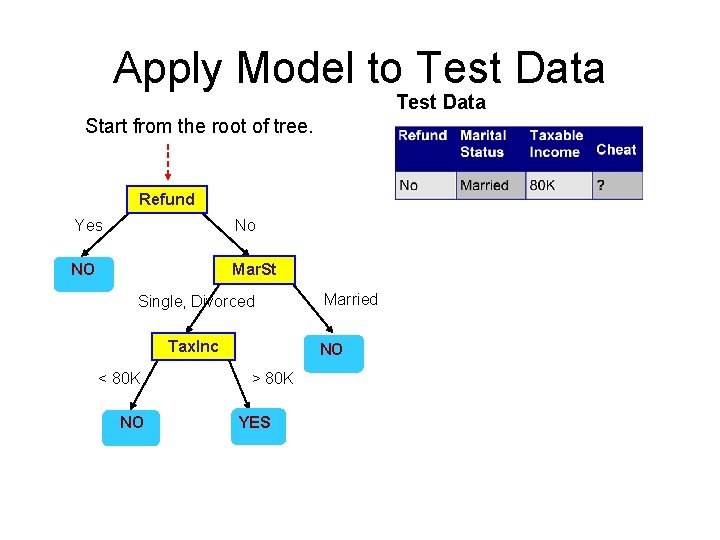
Apply Model to Test Data Start from the root of tree. Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES

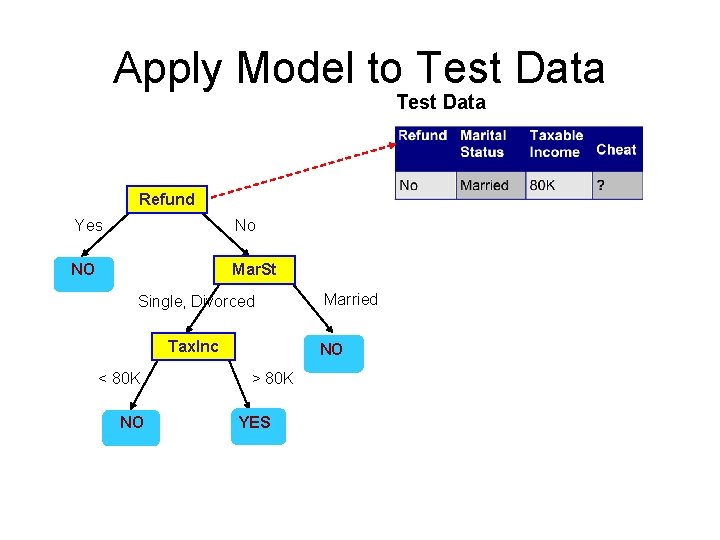
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES

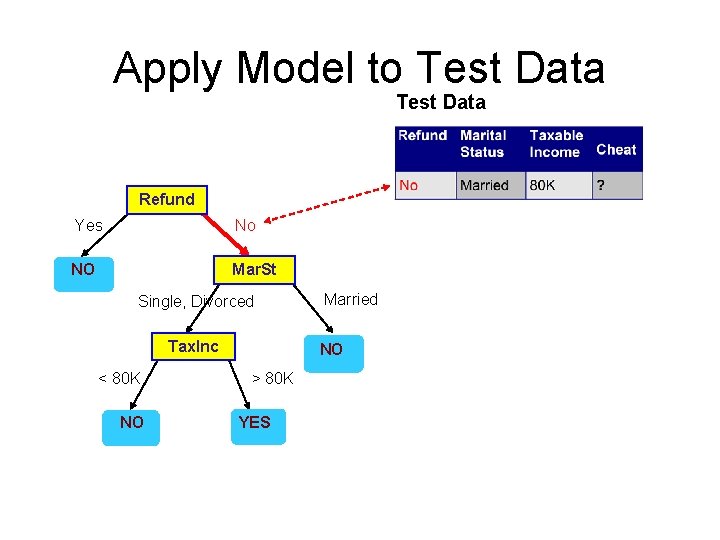
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES

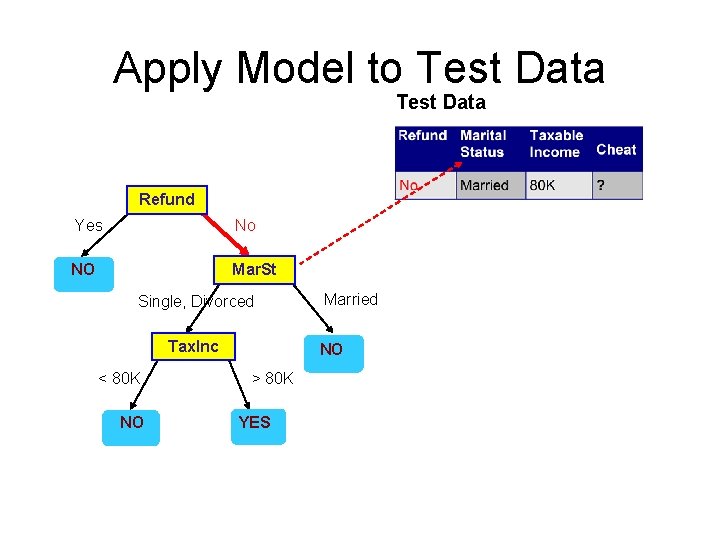
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES

Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES

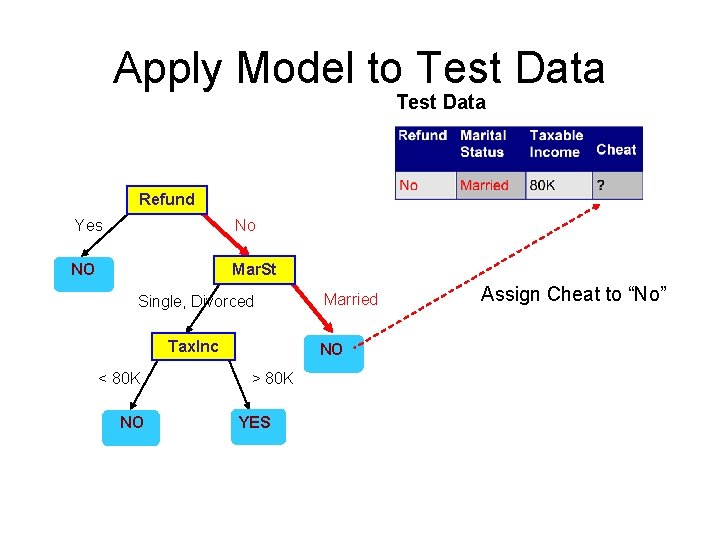
Apply Model to Test Data Refund Yes No NO Mar. St Single, Divorced Tax. Inc < 80 K NO Married NO > 80 K YES Assign Cheat to “No”

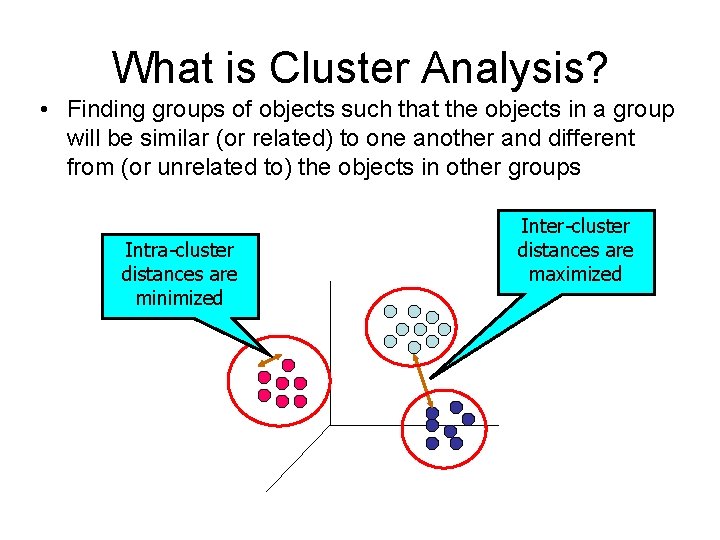
What is Cluster Analysis? • Finding groups of objects such that the objects in a group will be similar (or related) to one another and different from (or unrelated to) the objects in other groups Intra-cluster distances are minimized Inter-cluster distances are maximized

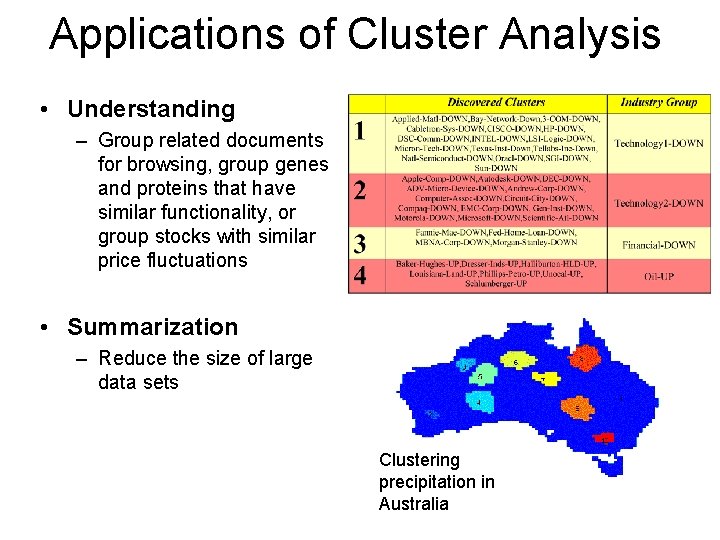
Applications of Cluster Analysis • Understanding – Group related documents for browsing, group genes and proteins that have similar functionality, or group stocks with similar price fluctuations • Summarization – Reduce the size of large data sets Clustering precipitation in Australia

Notion of a Cluster can be Ambiguous How many clusters? Six Clusters Two Clusters Four Clusters

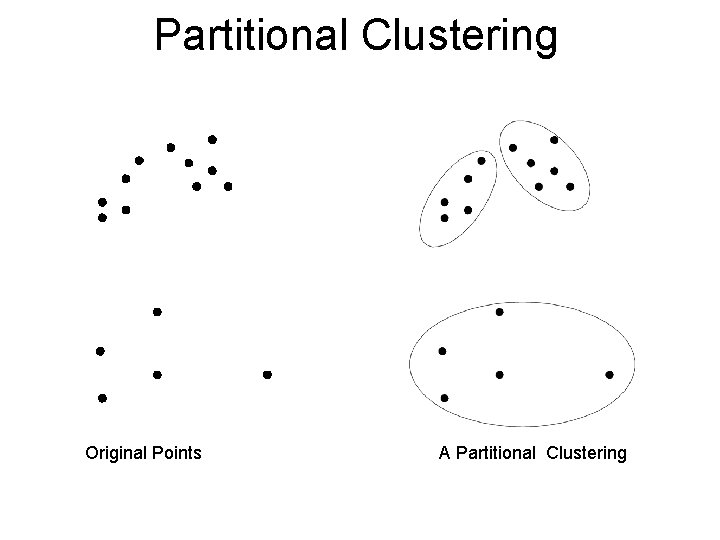
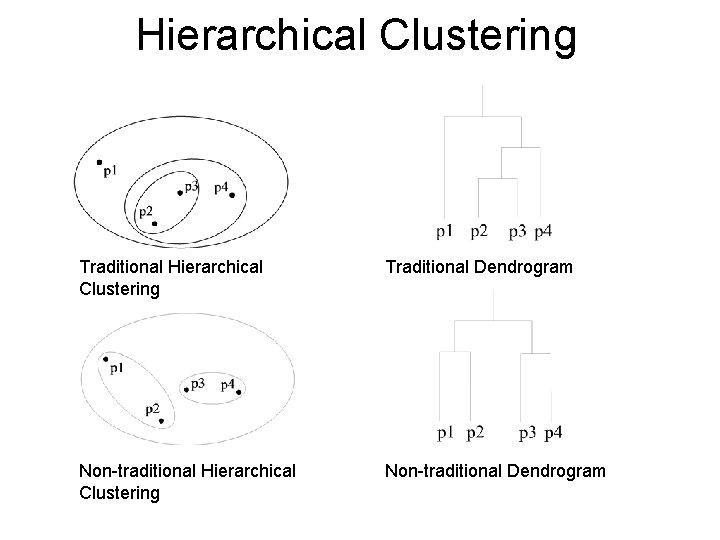
Types of Clusterings • A clustering is a set of clusters • Important distinction between hierarchical and partitional sets of clusters • Partitional Clustering – A division data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset • Hierarchical clustering – A set of nested clusters organized as a hierarchical tree

Partitional Clustering Original Points A Partitional Clustering

Hierarchical Clustering Traditional Dendrogram Non-traditional Hierarchical Clustering Non-traditional Dendrogram

Clustering Algorithms • K-means and its variants • Hierarchical clustering

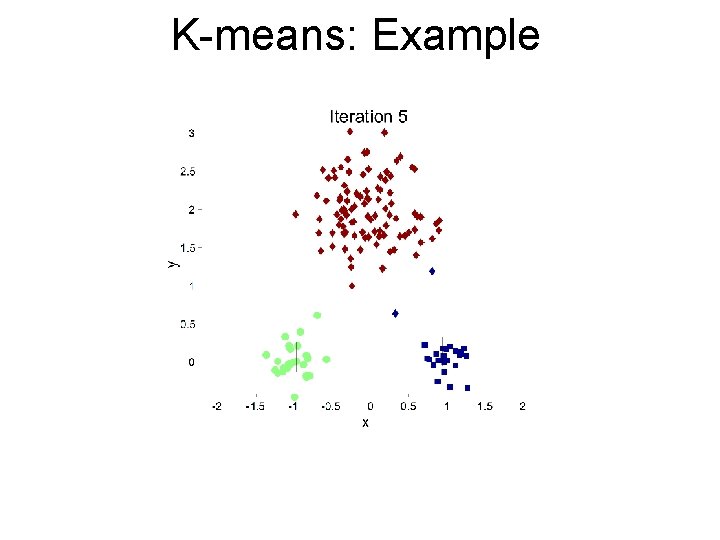
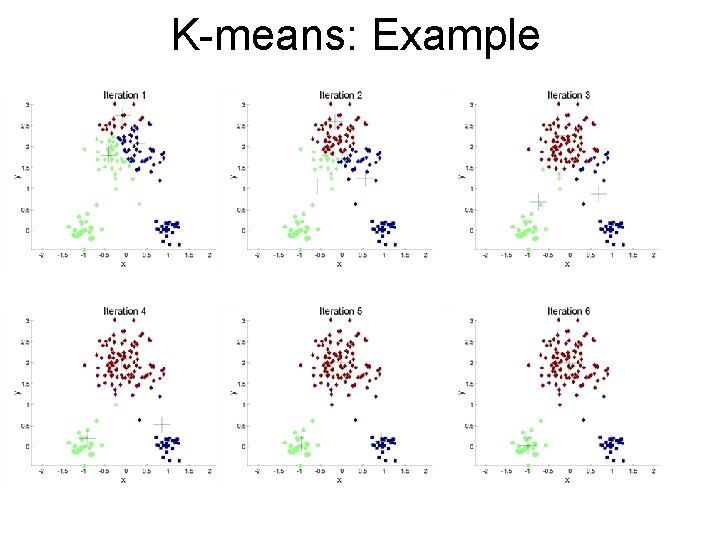
K-means Clustering • • • Partitional clustering approach Each cluster is associated with a centroid (center point) Each point is assigned to the cluster with the closest centroid Number of clusters, K, must be specified The basic algorithm is very simple

K-means: Example

K-means: Example

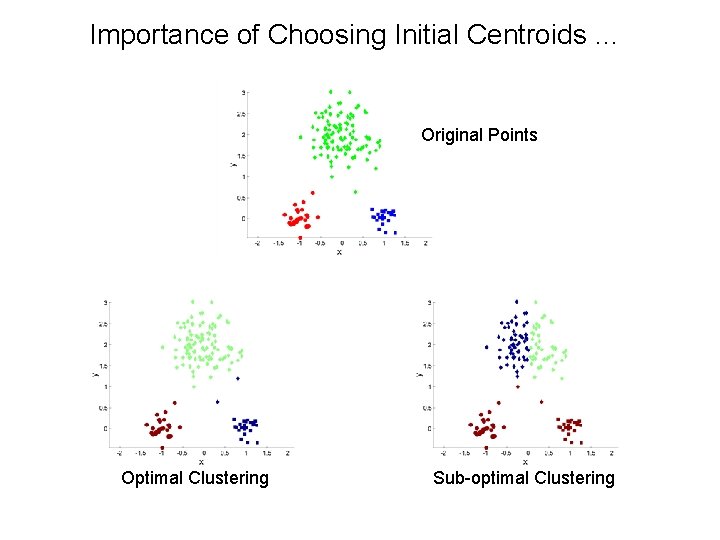
Importance of Choosing Initial Centroids … Original Points Optimal Clustering Sub-optimal Clustering

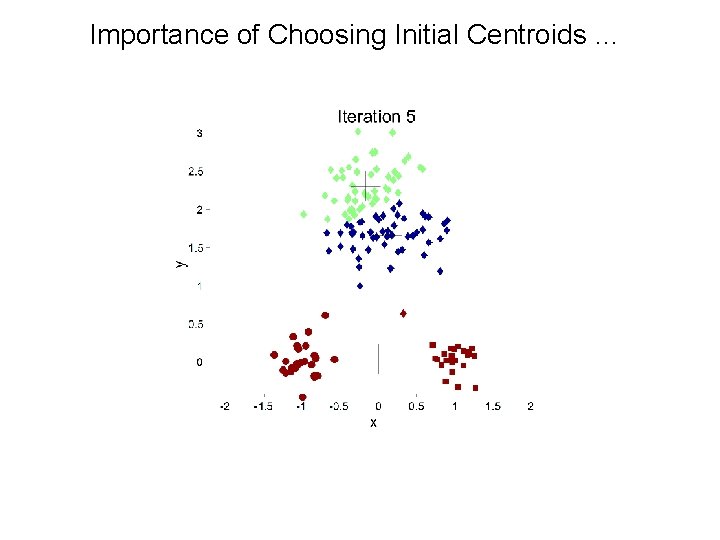
Importance of Choosing Initial Centroids …

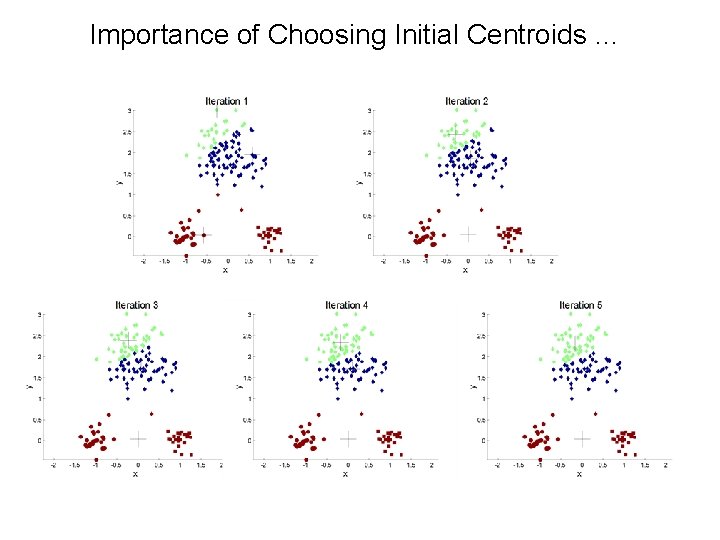
Importance of Choosing Initial Centroids …

Problems with Selecting Initial Points • If there are K ‘real’ clusters then the chance of selecting one centroid from each cluster is small. – – Chance is relatively small when K is large If clusters are the same size, n, then – – For example, if K = 10, then probability = 10!/1010 = 0. 00036 Sometimes the initial centroids will readjust themselves in ‘right’ way, and sometimes they don’t Consider an example of five pairs of clusters –

Solutions to Initial Centroids Problem • Multiple runs – Helps, but probability is not on your side • Sample and use hierarchical clustering to determine initial centroids • Select more than k initial centroids and then select among these initial centroids – Select most widely separated • Postprocessing

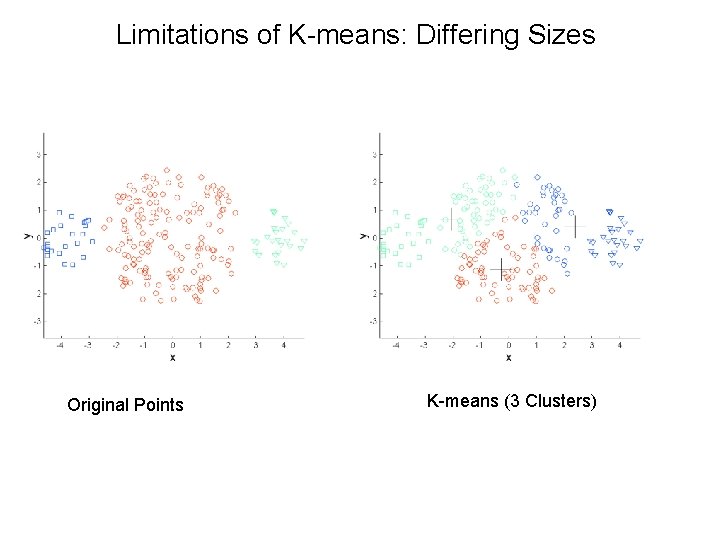
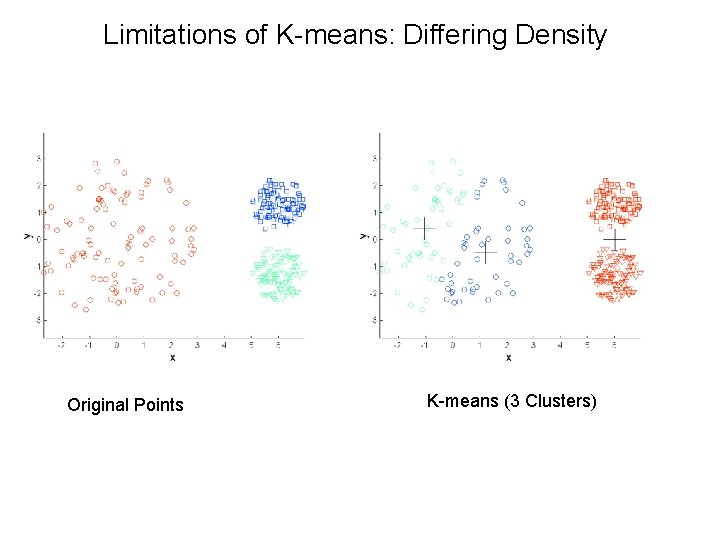
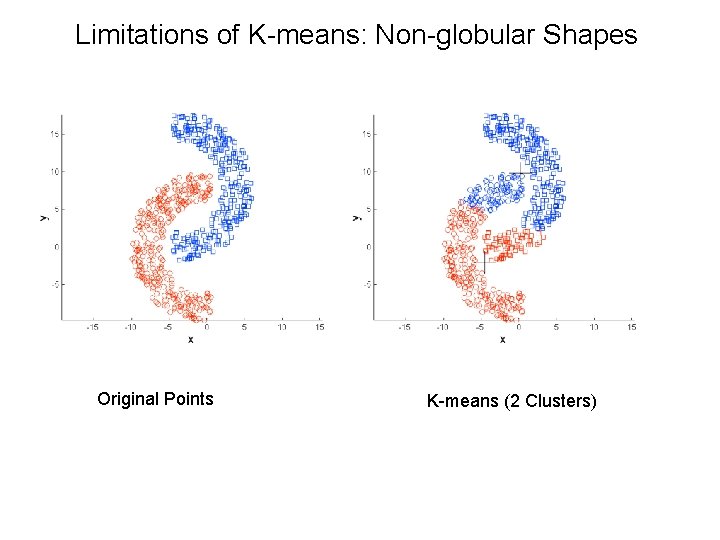
Limitations of K-means • K-means has problems when clusters are of differing – Sizes – Densities – Non-globular shapes • K-means has problems when the data contains outliers.

Limitations of K-means: Differing Sizes Original Points K-means (3 Clusters)

Limitations of K-means: Differing Density Original Points K-means (3 Clusters)

Limitations of K-means: Non-globular Shapes Original Points K-means (2 Clusters)

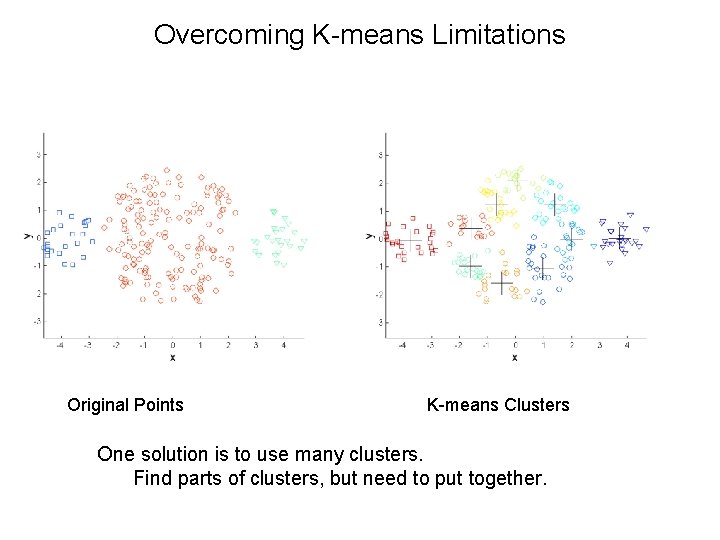
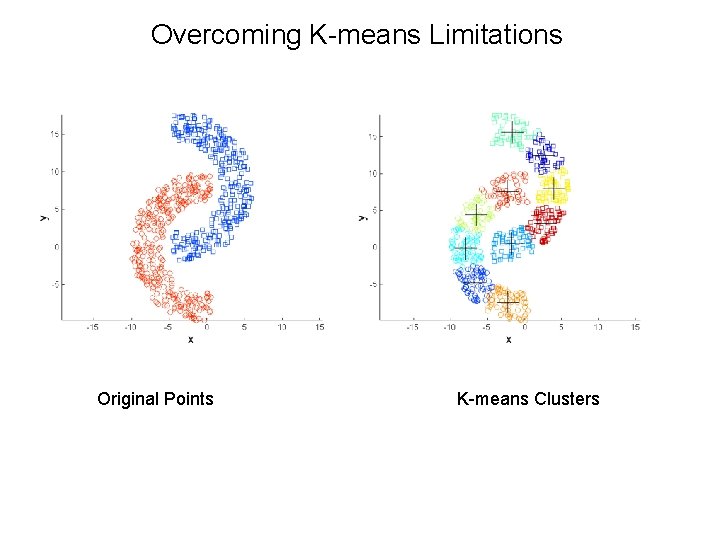
Overcoming K-means Limitations Original Points K-means Clusters One solution is to use many clusters. Find parts of clusters, but need to put together.

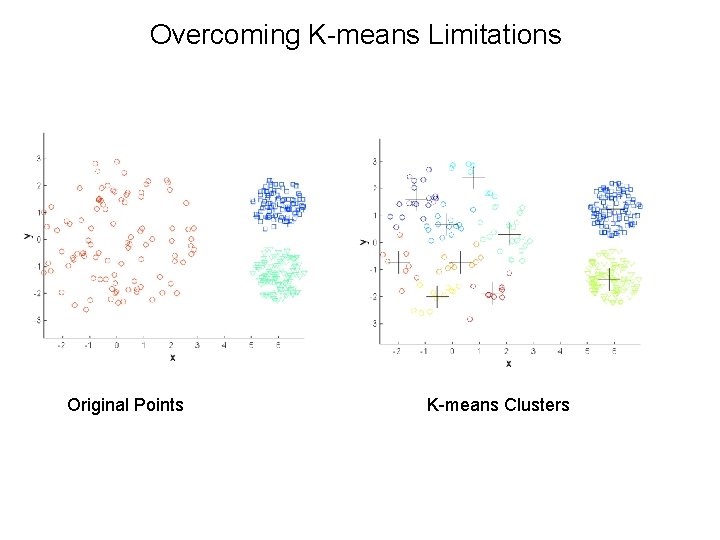
Overcoming K-means Limitations Original Points K-means Clusters

Overcoming K-means Limitations Original Points K-means Clusters

Clustering Algorithms • K-means and its variants • Hierarchical clustering

Hierarchical Clustering • Produces a set of nested clusters organized as a hierarchical tree • Can be visualized as a dendrogram – A tree like diagram that records the sequences of merges or splits

Strengths of Hierarchical Clustering • Do not have to assume any particular number of clusters – Any desired number of clusters can be obtained by ‘cutting’ the dendrogram at the proper level • They may correspond to meaningful taxonomies – Example in biological sciences (e. g. , animal kingdom, phylogeny reconstruction, …)

Hierarchical Clustering • Two main types of hierarchical clustering – Agglomerative: • Start with the points as individual clusters • At each step, merge the closest pair of clusters until only one cluster (or k clusters) left – Divisive: • Start with one, all-inclusive cluster • At each step, split a cluster until each cluster contains a point (or there are k clusters) • Traditional hierarchical algorithms use a similarity or distance matrix – Merge or split one cluster at a time

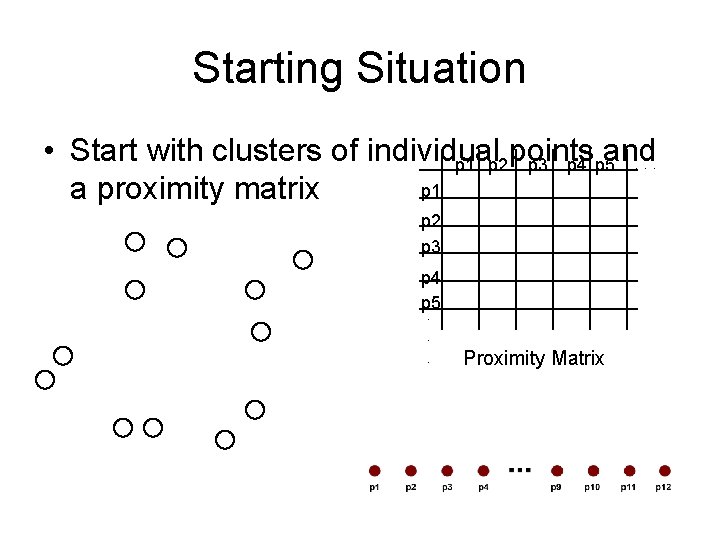
Agglomerative Clustering Algorithm • More popular hierarchical clustering technique • Basic algorithm is straightforward 1. 2. 3. 4. 5. 6. • Compute the proximity matrix Let each data point be a cluster Repeat Merge the two closest clusters Update the proximity matrix Until only a single cluster remains Key operation is the computation of the proximity of two clusters – Different approaches to defining the distance between clusters distinguish the different algorithms

Starting Situation • Start with clusters of individual points and p 1 p 2 p 3 p 4 p 5. . . p 1 a proximity matrix p 2 p 3 p 4 p 5. . . Proximity Matrix

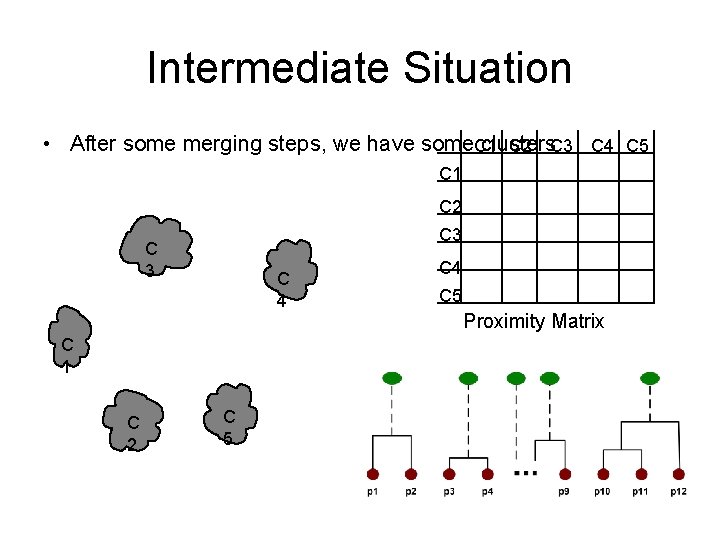
Intermediate Situation • After some merging steps, we have some. C 1 clusters C 2 C 3 C 4 C 5 C 1 C 2 C 3 C 4 C 1 C 2 C 5 C 4 C 5 Proximity Matrix

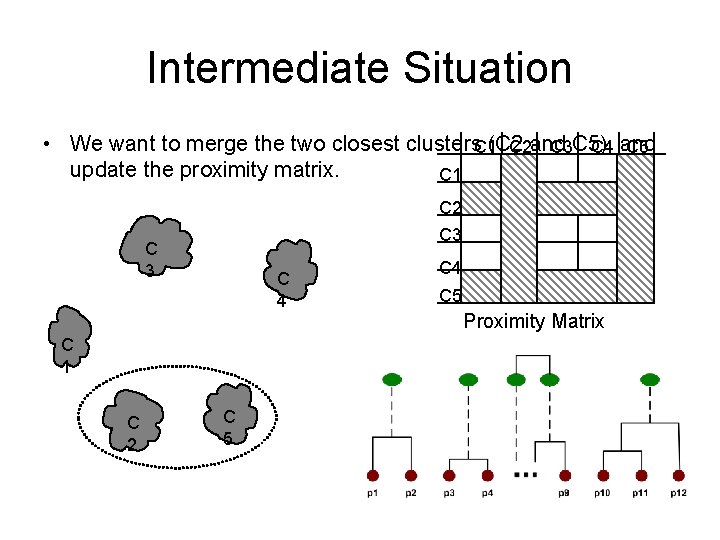
Intermediate Situation • We want to merge the two closest clusters. C 1(C 2 C 2 and C 3 C 5) C 4 and C 5 update the proximity matrix. C 1 C 2 C 3 C 4 C 1 C 2 C 5 C 4 C 5 Proximity Matrix

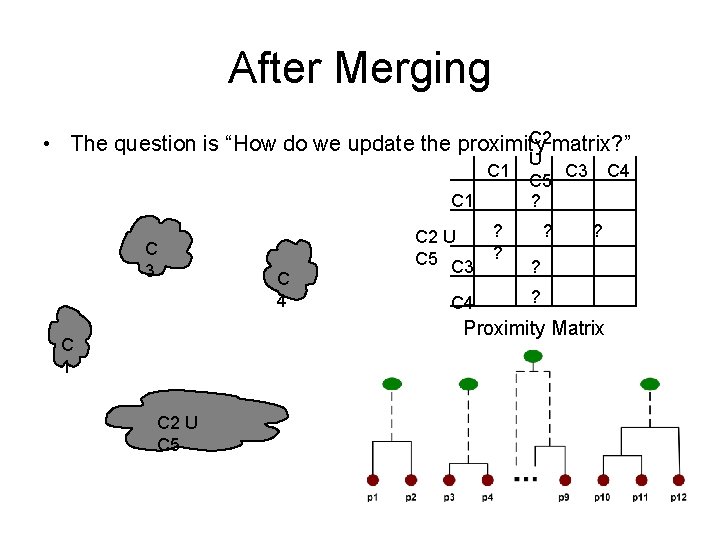
After Merging C 2 matrix? ” • The question is “How do we update the proximity C 1 C 3 C 4 C 2 U C 5 C 3 C 4 ? ? U C 3 C 5 ? ? C 4 ? ? ? Proximity Matrix C 1 C 2 U C 5

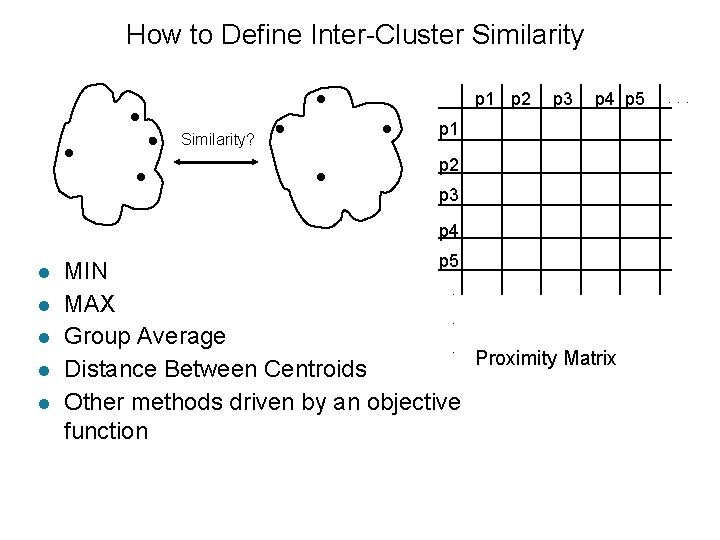
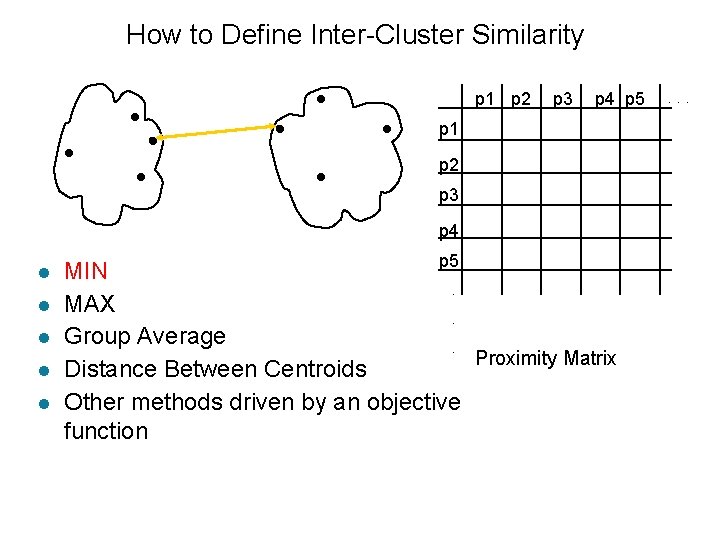
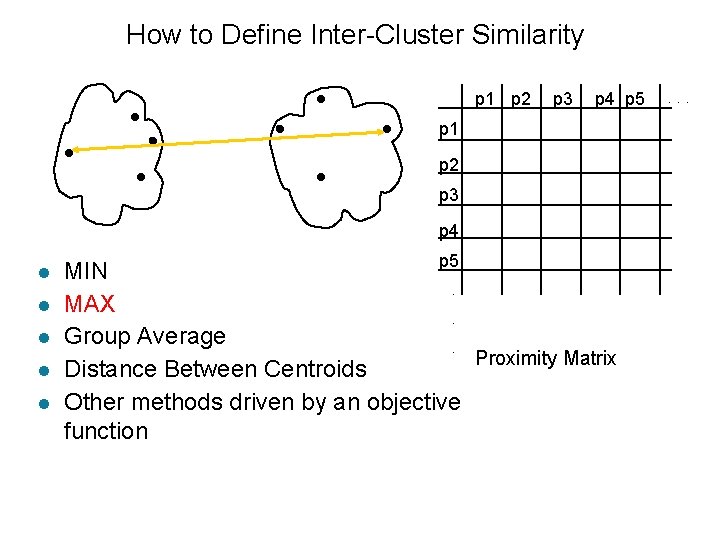
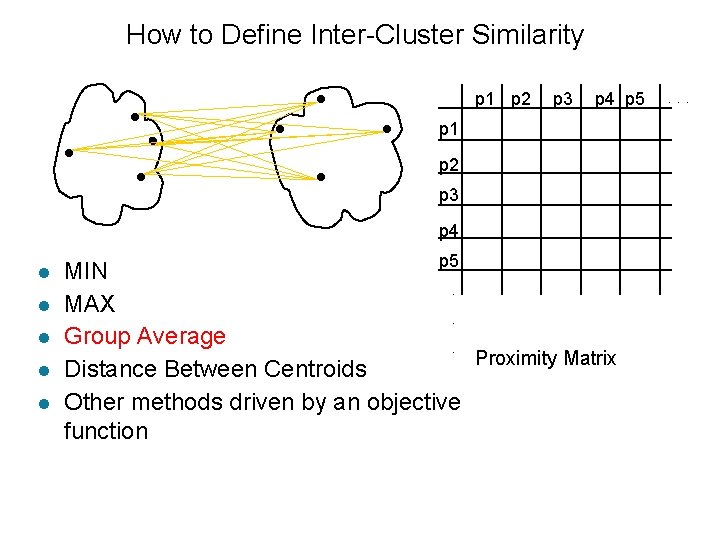
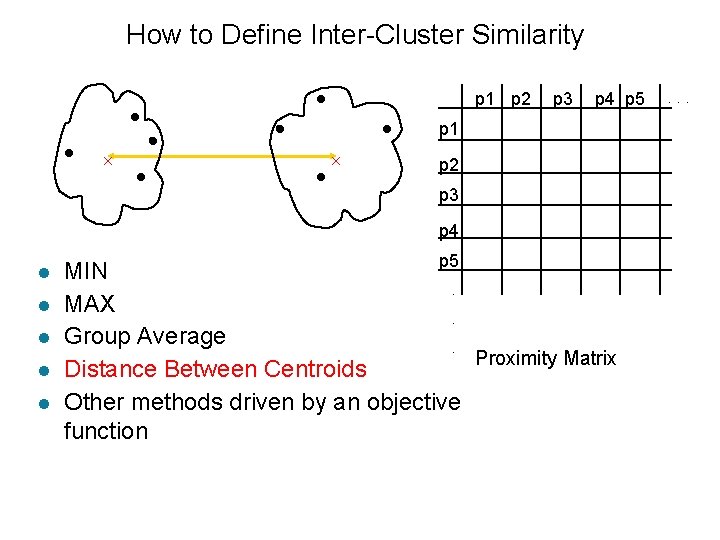
How to Define Inter-Cluster Similarity p 1 p 2 Similarity? p 3 p 4 p 5 p 1 p 2 p 3 p 4 l l l p 5 MIN. MAX. Group Average. Proximity Matrix Distance Between Centroids Other methods driven by an objective function . . .

How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 l l l p 5 MIN. MAX. Group Average. Proximity Matrix Distance Between Centroids Other methods driven by an objective function . . .

How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 l l l p 5 MIN. MAX. Group Average. Proximity Matrix Distance Between Centroids Other methods driven by an objective function . . .

How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 l l l p 5 MIN. MAX. Group Average. Proximity Matrix Distance Between Centroids Other methods driven by an objective function . . .

How to Define Inter-Cluster Similarity p 1 p 2 p 3 p 4 p 5 p 1 p 2 p 3 p 4 l l l p 5 MIN. MAX. Group Average. Proximity Matrix Distance Between Centroids Other methods driven by an objective function . . .

Hierarchical Clustering: Problems and Limitations • Once a decision is made to combine two clusters, it cannot be undone • No objective function is directly minimized • Different schemes have problems with one or more of the following: – Sensitivity to noise and outliers – Difficulty handling different sized clusters and convex shapes

Cluster Validity • For supervised classification we have a variety of measures to evaluate how good our model is – Accuracy, precision, recall • For cluster analysis, the analogous question is how to evaluate the “goodness” of the resulting clusters? • But “clusters are in the eye of the beholder”! • Then why do we want to evaluate them? – – To avoid finding patterns in noise To compare clustering algorithms To compare two sets of clusters To compare two clusters

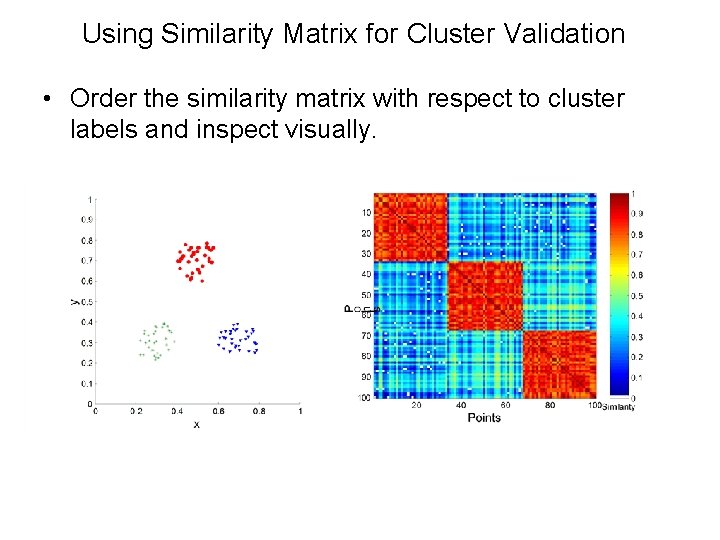
Using Similarity Matrix for Cluster Validation • Order the similarity matrix with respect to cluster labels and inspect visually.

Final Comment on Cluster Validity “The validation of clustering structures is the most difficult and frustrating part of cluster analysis. Without a strong effort in this direction, cluster analysis will remain a black art accessible only to those true believers who have experience and great courage. ” Algorithms for Clustering Data, Jain and Dubes