Data Integrity Algorithms and Security Requirements Agenda Cryptographic

Data Integrity Algorithms and Security Requirements

Agenda Cryptographic Hash Functions X. 509 Certificate, Kerberos SHA, SHA-3 IP Security Protocols Digital Signatures Web Security and Mail Security

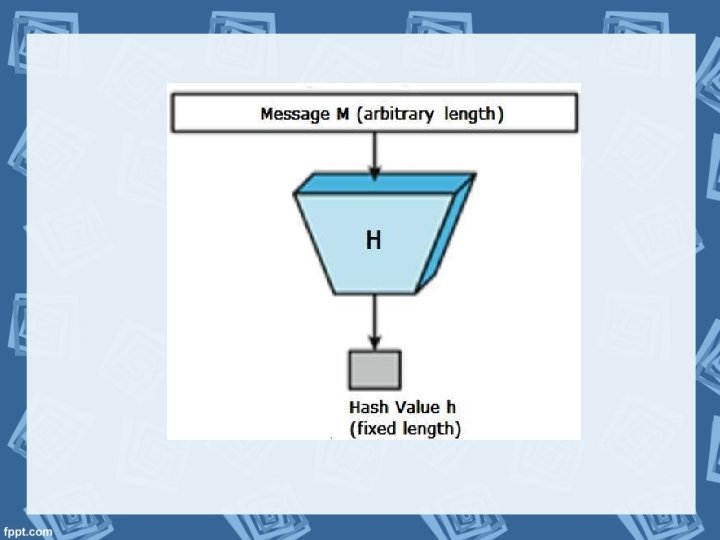
Cryptographic hash functions • A hash function is a mathematical function that converts a numerical input value into another compressed numerical value. • The input to the hash function is of arbitrary length but output is always of fixed length. • Values returned by a hash function are called message digest or simply hash values

Features of Hash Functions • Fixed Length Output (Hash Value): 512 bit or 160 bit output. • Computationally hash functions are much faster than a symmetric encryption.

Properties of Hash Functions • Pre-Image Resistance: computationally hard to reverse a hash function. • Second Pre-Image Resistance: It should be hard to find a different input with the same hash. • Collision Resistance: It should be hard to find two different inputs of any length that result in the same hash.

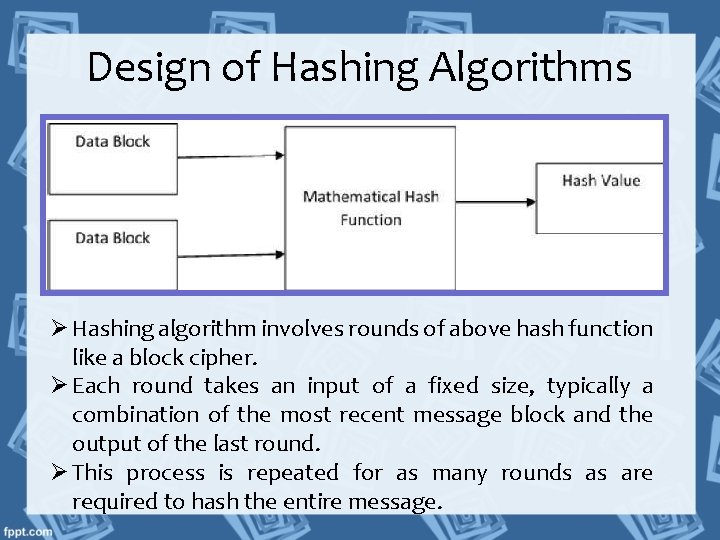
Design of Hashing Algorithms Ø Hashing algorithm involves rounds of above hash function like a block cipher. Ø Each round takes an input of a fixed size, typically a combination of the most recent message block and the output of the last round. Ø This process is repeated for as many rounds as are required to hash the entire message.

Popular Hash Functions Message Digest RIPEMD Secure Hash Algorithm Whirlpool

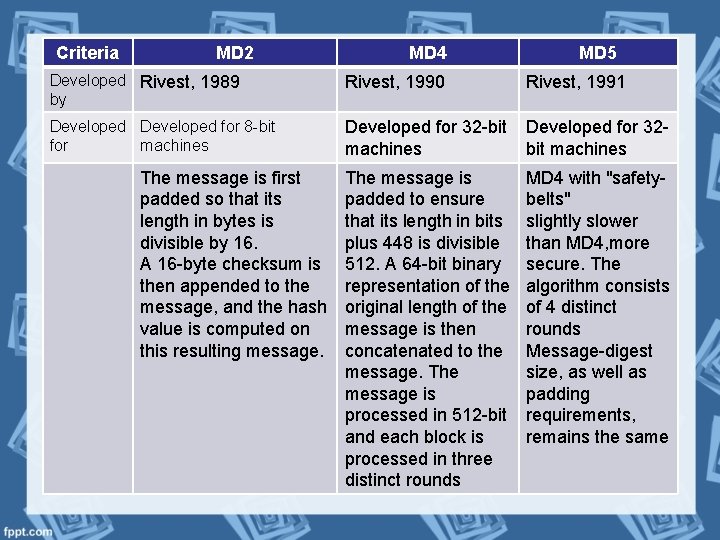
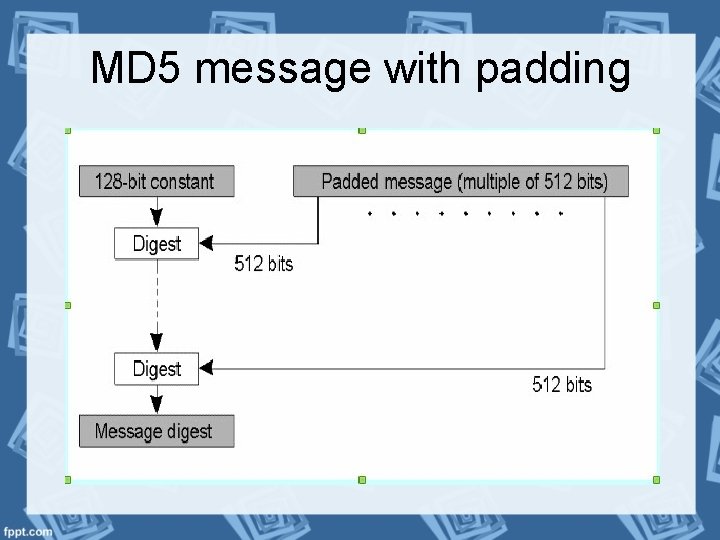
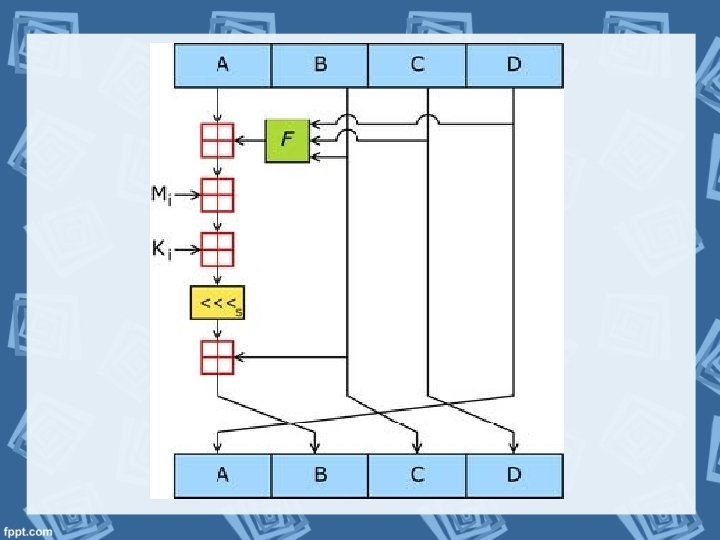
Criteria MD 2 MD 4 MD 5 Developed Rivest, 1989 by Rivest, 1990 Rivest, 1991 Developed for 8 -bit for machines Developed for 32 -bit machines Developed for 32 bit machines The message is padded to ensure that its length in bits plus 448 is divisible 512. A 64 -bit binary representation of the original length of the message is then concatenated to the message. The message is processed in 512 -bit and each block is processed in three distinct rounds MD 4 with "safetybelts" slightly slower than MD 4, more secure. The algorithm consists of 4 distinct rounds Message-digest size, as well as padding requirements, remains the same The message is first padded so that its length in bytes is divisible by 16. A 16 -byte checksum is then appended to the message, and the hash value is computed on this resulting message.

Criteria Possible attacks MD 2 Rogier and Chauvaud have found that collisions for MD 2 can be constructed if the calculation of the checksum is omitted MD 4 MD 5 Attacks on versions of MD 4 with either the first or the last rounds missing were developed very quickly by Den Boer and Bosselaers. Dobbertin has shown how collisions for the full version of MD 4 can be found in under a minute on a typical PC Den Boer and Bosselaers have found pseudocollisions for MD 5 Van Oorschot and Wiener have considered a brute-force search for collisions in hash functions, and they estimate that a collision search machine designed specifically for MD 5 (costing $10 million in 1994) could find a collision for MD 5 in 24 days on average. The general techniques can be applied to other hash functions.

MD 5 • Brute force is not possible with MD 5

MD 5 message with padding

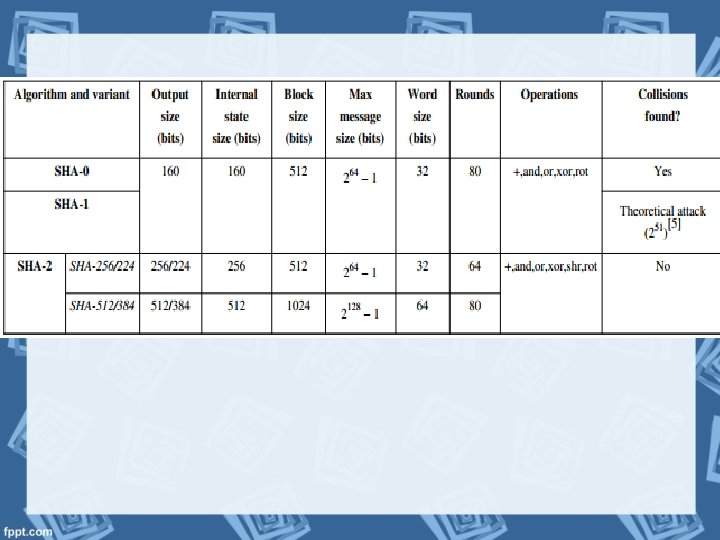
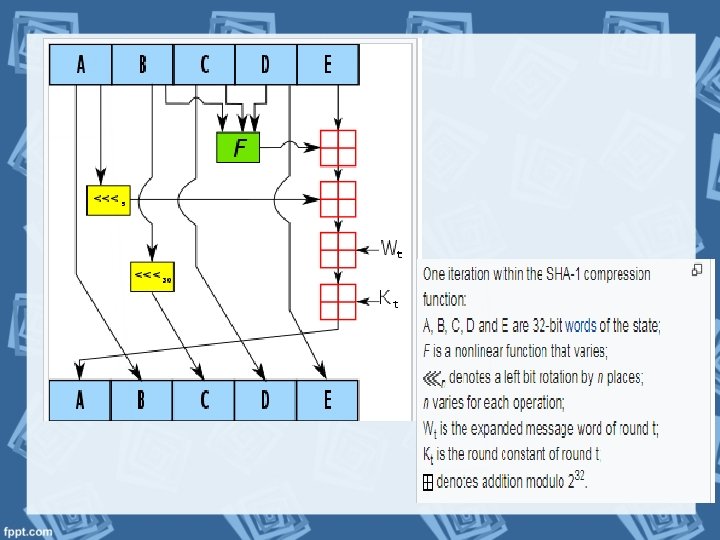
Secure Hash Algorithm (SHA-1)