DATA HANDLING MATHEMATICS GRADE 11 REQUIREMENTS For this

DATA HANDLING MATHEMATICS GRADE 11

REQUIREMENTS: For this lesson, you would need the following: q. Math instrument set q. Scientific calculator q. Classwork/ Homework book q. Access to the internet

LEARNING OUTCOMES LO 4 The learner must be able to: q. Collect q. Display q. Analyse q. Apply knowledge of statistics and probability to communicate, justify, predict and critically interrogate findings and draw conclusions.

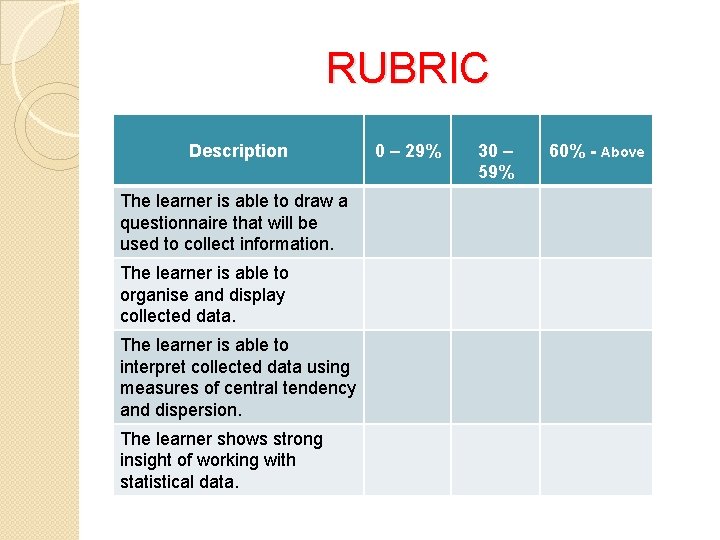
RUBRIC Description The learner is able to draw a questionnaire that will be used to collect information. The learner is able to organise and display collected data. The learner is able to interpret collected data using measures of central tendency and dispersion. The learner shows strong insight of working with statistical data. 0 – 29% 30 – 59% 60% - Above

INTRODUCTION Data Handling is the use of sample data to explain the characteristics and behaviour of larger populations. This study involves the collection, organisation, presentation and analysis of such sample data.

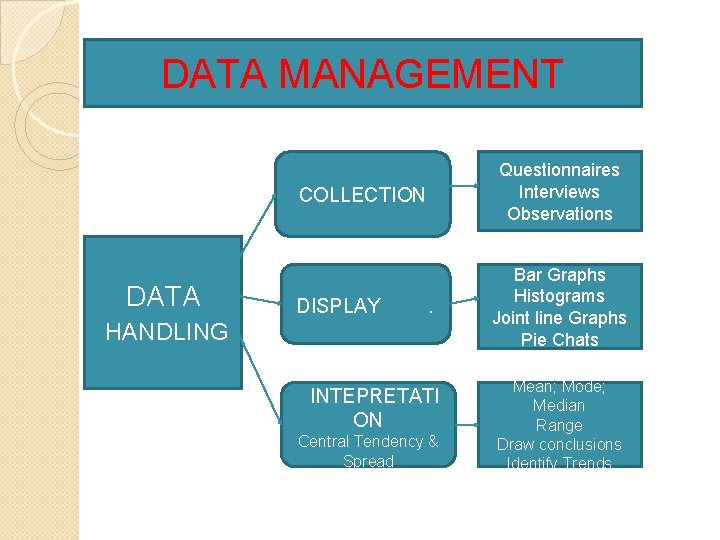
DATA MANAGEMENT Questionnaires Interviews Observations COLLECTION DATA DISPLAY . HANDLING INTEPRETATI ON Central Tendency & Spread Bar Graphs Histograms Joint line Graphs Pie Chats Mean; Mode; Median Range Draw conclusions Identify Trends.

E. g. Teenage pregnancy in South African schools A typical example of the application of data handling is when the statistician wants to show widespread teenage pregnancy is in the schooling system. She collects data from the clinics in identified areas, organise this data, represent it, analyse it and finally gives a picture of the problem for the whole country. It is worthy to note the statistician did not go to all the clinics in the country, but went to a few. But her results are generalised for the entire country.

COLLECTION OF DATA 1. 2. 3. 4. Please fill the details. Tick the relevant blocks. What age group do you belong to? Under 16 16 – 25 26 – 35 Are you? Female Male Do you have a driver’s licence? Yes No What is the youngest age individuals should be allowed to apply for the driver’s licence? years old.

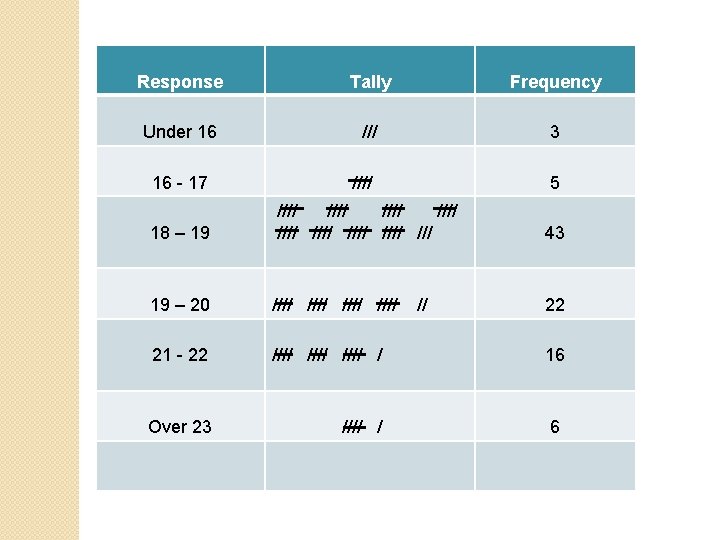
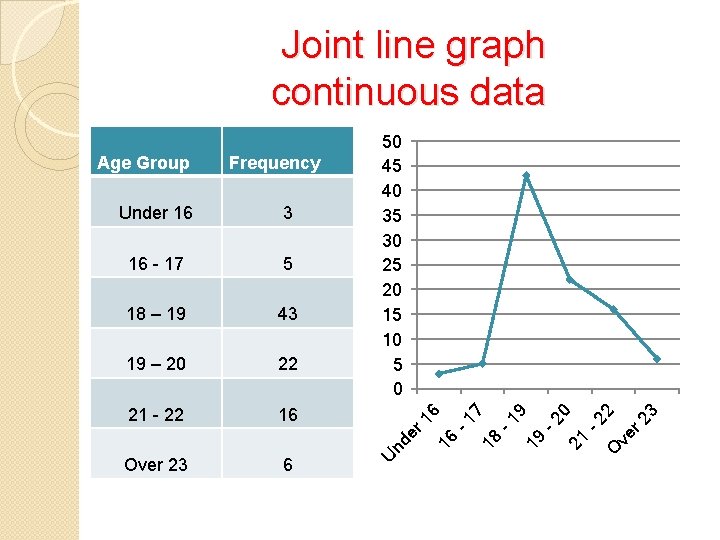
DISPLAY OF DATA After questionnaires have been filled and returned, the data they contain has to be sorted. The most popular way of sorting data is by tally/frequency tables. E. g. Malose conducted a survey to determine the minimum age for a girl to marry. The results are displayed in the next slide using the tally and frequency table:

Response Tally Frequency Under 16 /// 3 16 - 17 //// 5 18 – 19 //// //// /// 43 19 – 20 //// 22 21 - 22 //// / 16 Over 23 //// / 6 //

ACTIVITY 1 The death penalty is one of the most controversial issues of your times. Draw a questionnaire to determine how many people still think it is an effective way of meting out punishment. In your questionnaire, respondents should be asked personal details like age, level of education, gender and crimes they think deserve death as punishment.

CHOOSING THE RIGHT GRAPH When data has been sorted out, the right graph has to be chosen to display the data. There are two kinds of data: q. Discrete data. q. Continuous data. The following slide explains the two kinds of data.

Discrete data This is information about certain definite, separate values or quantities, e. g. Data about number of houses, types of cars, populations per province or state, etc. E. g. There are either 500 or 501 houses in a township. There cannot be 500, 6 houses. Continuous data This is information that can take on any value within certain boundaries. Data about height, mass or age are examples of continuous data. E. g. An age of 12 years can be from 12 years and 3 months to 12 years and 11 months. CLASSIFICATION OF DATA.

ACTIVITY 2 As you have noticed, classifying data is very crucial to deciding the graph to use. The data collected by Malose about the minimum age for a girl to marry can be classified as discrete. Is this statement True or False? Check on the Assessment tab of the website for the correct answer.

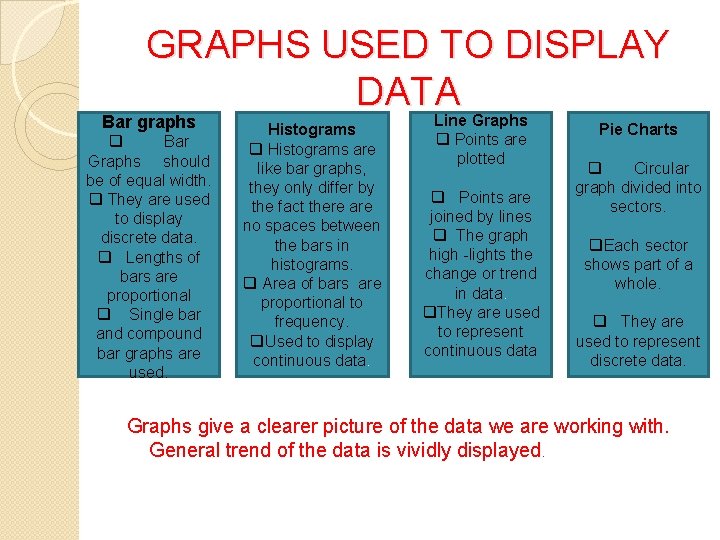
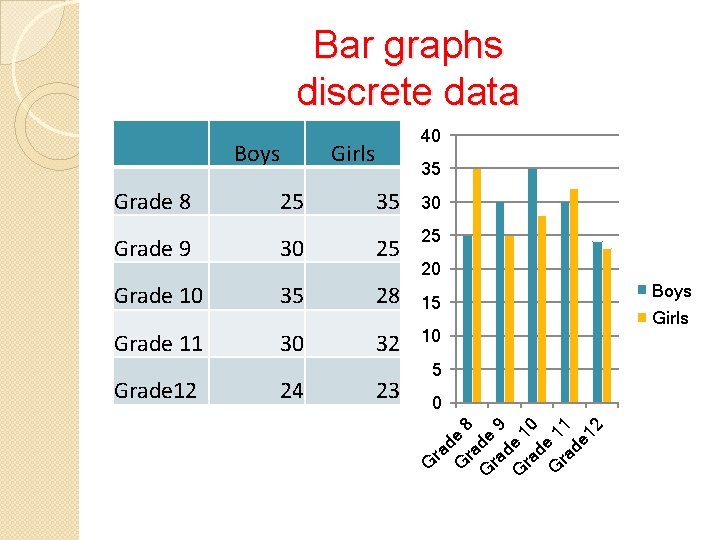
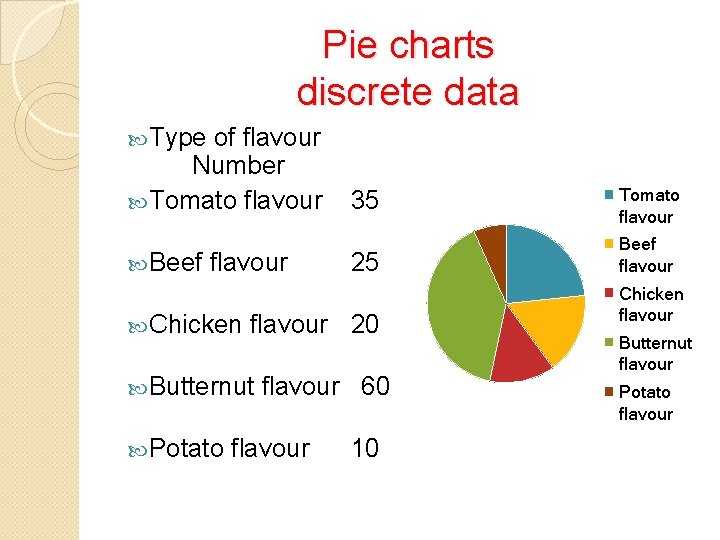
GRAPHS USED TO DISPLAY DATA Bar graphs Mm q Bar Graphs should be of equal width. q They are used to display discrete data. q Lengths of bars are proportional q Single bar and compound bar graphs are used. Histograms q Histograms are like bar graphs, they only differ by the fact there are no spaces between the bars in histograms. q Area of bars are proportional to frequency. q. Used to display continuous data. Line Graphs q Points are plotted q Points are joined by lines q The graph high -lights the change or trend in data. q. They are used to represent continuous data Pie Charts q Circular graph divided into sectors. q. Each sector shows part of a whole. q They are used to represent discrete data. Graphs give a clearer picture of the data we are working with. General trend of the data is vividly displayed.

Joint line graph continuous data U 2 O ve r 2 3 6 -2 Over 23 0 16 21 21 - 22 -2 22 9 19 – 20 19 43 -1 18 – 19 7 5 18 16 - 17 -1 3 nd er Under 16 16 Frequency 16 Age Group 50 45 40 35 30 25 20 15 10 5 0

Bar graphs discrete data Boys 40 Girls 35 Grade 8 25 35 30 Grade 9 30 25 25 Grade 10 35 28 15 Grade 11 30 32 10 24 23 5 0 G ra d G e 8 ra G de ra 9 d G e 1 ra 0 de G 1 ra 1 de 12 Grade 12 20 Boys Girls

Pie charts discrete data Type of flavour Number Tomato flavour Beef flavour Chicken Tomato flavour 25 Beef flavour 20 Butternut Potato 35 flavour 60 flavour 10 Chicken flavour Butternut flavour Potato flavour

Measures of central tendency • Mean: This is an average of a data set, defined by the formula: sum of all values/ number of values Median: It is the middle value of the data set. This value is only determined after data is arranged in ascending order. Mode: It is the value which appears most frequent in a data set.

Example of the mean Calculate the mean length of the three main rivers, Orange(2 250 km); Limpopo(1 600 km) and Vaal (1 160 km) Answer: Mean

EXAMPLE OF MEDIAN Determine the median of Malose’s marks for: v English: 6 8 9 3 1 4 6 v Mathematics: 79486483 marks. English Solutionthe 1: Arrange size: 134466689 Middle The median mark for English is 6. Solution 2: Arrange the Math marks in order of size: 3 4 4 6 7 8 8 9 The median lies half way between 6 Middle and 7. The median mark for maths is 6. 5.

EXAMPLES OF THE MODE Determine the mode of the given data sets: q 1 6 2 0 4 2 1 2 2 4 q 4 2 1 2 5 4 7 3 2 4 q 3 6 4 5 1 2 7 • It is advisable to arrange the data in ascending order. It now becomes evident that: q 2 appears more frequent in data set 1. Therefore 2 is the mode. q 2 and 4 are the modes for data set 2. q There is no mode for data set 3

Activity 3 The following data sets are Senzo’s marks for English and Mathematics respectively. 689314646 794864836 Indicate whether the following statement is True or False by choosing the correct tab on Assessment Page of the website. The median of both data sets is 6.

Bibliography http: //www. motifake. com/tags/teen Fourie, D & Olivier, S; 2008; Spot On Mathematical Literacy GRD 11, pp 199 – 245 http: //www. cimt. plymouth. ac. uk/projects/mepres/bo ok 7/bk 7 i 18/bk 7_18 i 2. htm+