DATA FLOW ANALYSIS HOW TO ANALYZE LANGUAGES AUTOMATICALLY

Agenda n n n n Quick recap (of everything so far): "Putting it all

Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [3] Aug 11, 2010

We (only) need 3 things: § A control-flow graph § A lattice § Transfer

Solve Equations : -) n One big lattice: n n 1 big abstract value

The Entire Process : -) Program: 1. Control-flow graph: 5. Solve rec. equations…: T

Exercise: n Repeat this process for program (of two vars): n n x =

Naïve Fixed-Point Algorithm n Naïve Fixed-Point Algorithm: n …uses intermediate ”results” from previous iteration:

Chaotic Iteration Algorithm n Chaotic Iteration Algorithm: n …exploits ”forward nature” of program control

Work-list Algorithm n Work-list Algorithm: n …uses a ”queue” to control (optimize) computation: Pop

The Language ’C--’ n Syntactic Categories: n Expressions (E EXP): n n E :

Control-Flow Graph (for ’C--’) n Inductively defined control-flow graph: v : = E 1

Sign Analysis: Lattice n Lattice: LSIGN: n n ENVLattice: Confluence operator: n = ’(

Sign Analysis: Transfer F’s n Transfer Functions: Env[x ] Env[x sign(Env, Exp)] Claus Brabrand,

Inductive definition of ’sign’ in the syntactic structure of Exp n Syntax: E :

Exercise: n n n Come up with a program the analysis… A) n can

Const Propagation: Lattice n Lattice: LNUM: n n ENVLattice: LNUM|VAR| VAR LNUM Confluence operator:

Const Propagation: Transfer F’s n Transfer Functions: Env[x ] Env[x eval(Env, Exp)] Claus Brabrand,

Inductive definition of ’eval’ in the syntactic structure of Exp n Syntax: E :

Initialized Variables Analysis n possibly uninitialized Lattice: Note: It’s always "safe" to answer "too

Initialized Variables Analysis n Transfer Functions: Env[x ] Env[x init(Env, Exp)] Claus Brabrand, UFPE,

Inductive definition of ’init’ in the syntactic structure of Exp n Syntax: E :

Note: Isomorphism! n With value lattice: n ENV-lattice is isomorphic to: n …for every

Initialized Variables Analysis (Revisited) n ENV-lattice: n Vars that are possibly uninitialized n Transfer

Set-based analyses… {may, must} {forwards, backwards} Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS Aug 11,

Forwards vs. Backwards? depends Analyze info that on past behavior n What you have

May vs. m. Must? ay t Analyze info that mupsaths definitely be true Analyze

WORKSHOP n Reaching Definitions: n n Live Variables: n n ' ' (backward), '

Reaching Definitions n Reaching Definitions: DEF-USE graph: n The reaching definitions (for a given

WHY do we do this? ”Learning takes place through the active behavior of the

WORKSHOP n n n 1) Define the problem 2) Show that the problem is

Now, please: 3’ recap n Please spend 3' on thinking about and writing down

Slides: 41

Download presentation

DATA - FLOW ANALYSIS [ HOW TO ANALYZE LANGUAGES AUTOMATICALLY ] Claus Brabrand ((( brabrand@itu. dk ))) Associate Professor, Ph. D. ((( Programming, Logic, and Semantics ))) IT University of Copenhagen Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS Aug 11, 2010

Agenda n n n n Quick recap (of everything so far): "Putting it all together" Data-Flow Analysis Fixed-Point Iteration Strategies (3 x) "Sign Analysis" 3 Example "Constant Propagation Analysis" Data-Flow Analyses "Initialized Variables Analysis" Set-Based Analysis Framework WORKSHOP Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [2] Aug 11, 2010

Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [3] Aug 11, 2010

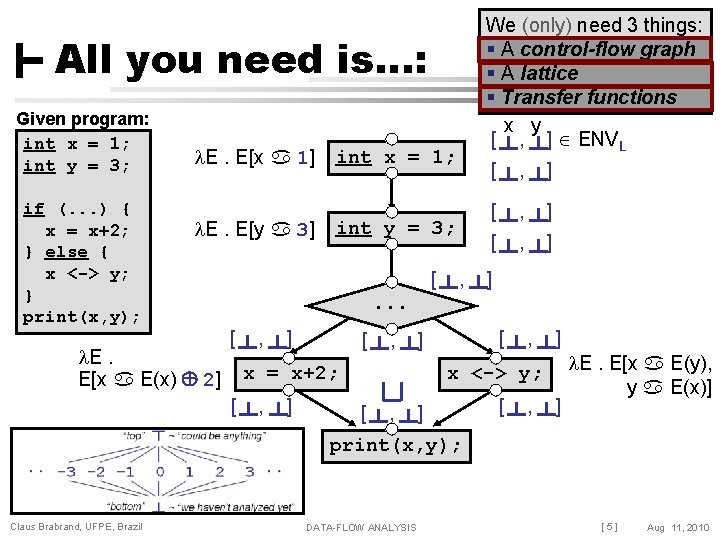
We (only) need 3 things: § A control-flow graph § A lattice § Transfer functions x y [ , ] ENVL All you need is…: Given program: int x = 1; int y = 3; if (. . . ) { x = x+2; } else { x <-> y; } print(x, y); E. E[x 1] E. E[y 3] E. E[x E(x) 2] int x = 1; int y = 3; [ , ] ] . . . [ , ] [ , x = x+2; [ , ] [ ] , ] x <-> y; [ , ] E. E[x E(y), y E(x)] print(x, y); Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [5] Aug 11, 2010

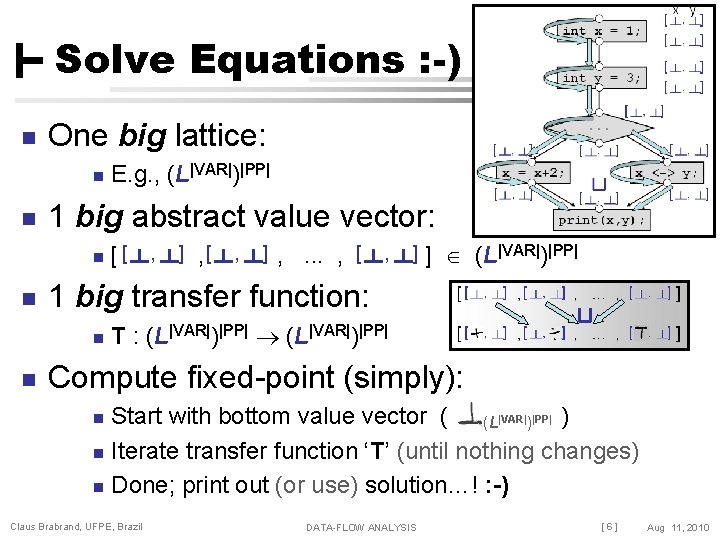
Solve Equations : -) n One big lattice: n n 1 big abstract value vector: n n [ [ , ] , . . . , [ , ] ] (L|VAR|)|PP| 1 big transfer function: n n E. g. , (L|VAR|)|PP| T : (L|VAR|)|PP| Compute fixed-point (simply): Start with bottom value vector ( (L|VAR|)|PP| ) n Iterate transfer function ‘T’ (until nothing changes) n Done; print out (or use) solution…! : -) n Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [6] Aug 11, 2010

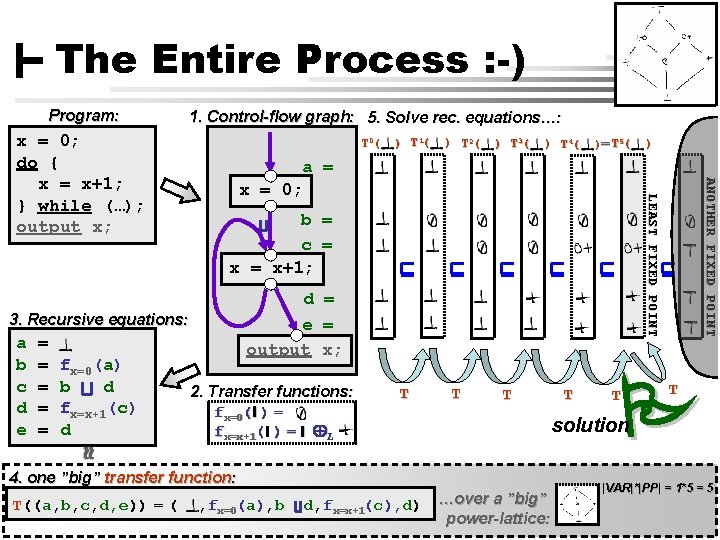
The Entire Process : -) Program: 1. Control-flow graph: 5. Solve rec. equations…: T 0( fx=0(a) b d fx=x+1(c) d ) T 3( ) T 4( b = c = x+1; d = e = output x; 2. Transfer functions: fx=0(l ) = fx=x+1(l ) = l L T T T Claus Brabrand, UFPE, Brazil , fx=0(a), b ) d, fx=x+1(c), d) DATA-FLOW ANALYSIS T T T solution 4. one ”big” transfer function: T((a, b, c, d, e)) = ( )= T 5( ANOTHER FIXED POINT = = = ) T 2( a = x = 0; 3. Recursive equations: a b c d e ) T 1( LEAST FIXED POINT x = 0; do { x = x+1; } while (…); output x; …over a ”big” power-lattice: |VAR|*|PP| = 1*5 = 5 [7] Aug 11, 2010

Exercise: n Repeat this process for program (of two vars): n n x = 1; y = 0; while (v>w) { x <-> y; } y = y+1; …using lattice: i. e. , determine…: 1) Control-flow graph n 2) Transfer functions n 3) Recursive equations n 4) One ”big” transfer function n 5) Solve recursive equations : -) n Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [8] Aug 11, 2010

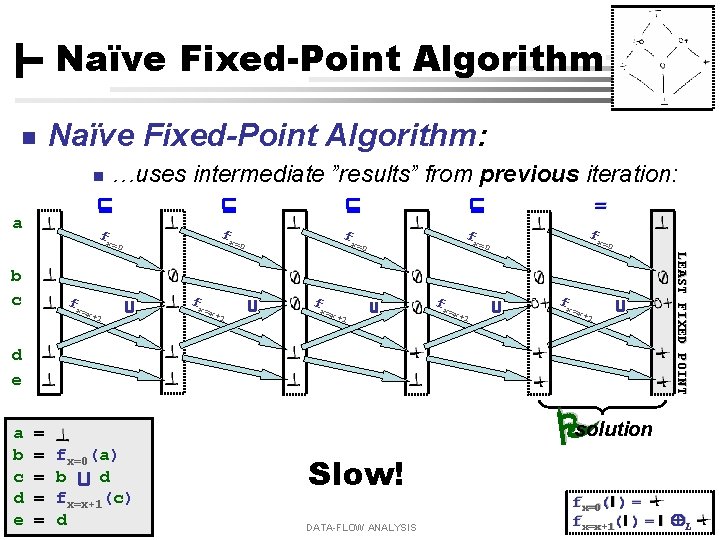
Naïve Fixed-Point Algorithm n Naïve Fixed-Point Algorithm: n …uses intermediate ”results” from previous iteration: = a fx fx fx =x+ 1 =0 =0 =0 fx =x+ 1 d e a = b = fx=0(a) c = b d d = fx=x+1(c) e = d Claus Brabrand, UFPE, Brazil Slow! DATA-FLOW ANALYSIS LEAST FIXED POINT b c fx fx fx =0 =0 solution fx=0(l ) = fx=x+1 l 11, L 2010 [ 10 ( ] l) = Aug

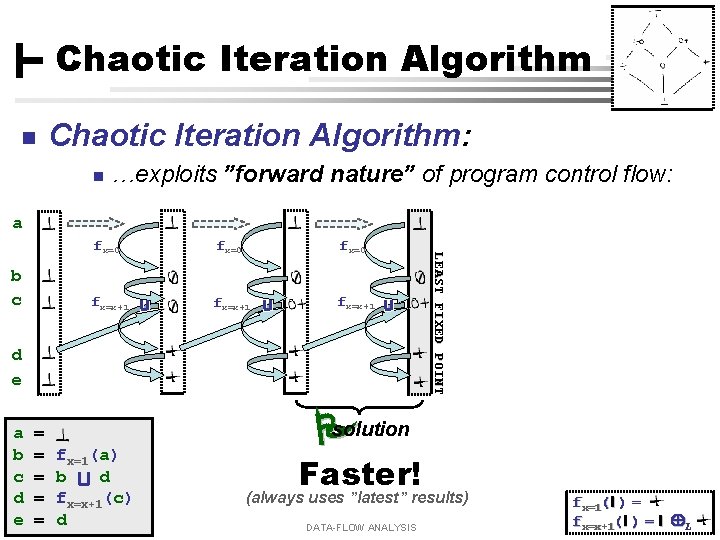
Chaotic Iteration Algorithm n Chaotic Iteration Algorithm: n …exploits ”forward nature” of program control flow: a fx=0 fx=x+1 d e a = b = fx=1(a) c = b d d = fx=x+1(c) e = d Claus Brabrand, UFPE, Brazil LEAST FIXED POINT b c fx=0 solution Faster! (always uses ”latest” results) DATA-FLOW ANALYSIS fx=1(l ) = fx=x+1 l 11, L 2010 [ 11 ( ] l) = Aug

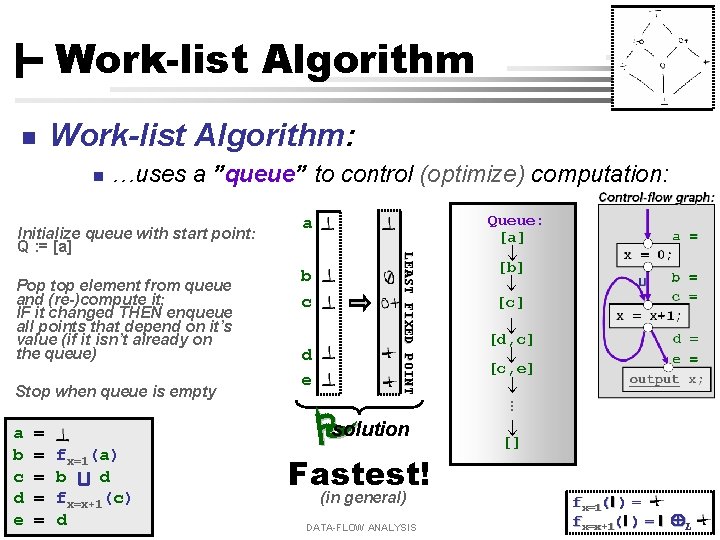
Work-list Algorithm n Work-list Algorithm: n …uses a ”queue” to control (optimize) computation: Pop top element from queue and (re-)compute it; IF it changed THEN enqueue all points that depend on it’s value (if it isn’t already on the queue) a = b = fx=1(a) c = b d d = fx=x+1(c) e = d Claus Brabrand, UFPE, Brazil b c d e solution Fastest! (in general) DATA-FLOW ANALYSIS [b] [c] [d, c] [c, e] … Stop when queue is empty Queue: [a] a LEAST FIXED POINT Initialize queue with start point: Q : = [a] [] fx=1(l ) = fx=x+1 l 11, L 2010 [ 12 ( ] l) = Aug

The Language ’C--’ n Syntactic Categories: n Expressions (E EXP): n n E : | n | v | E + E’ E * E’ | E == E’ | | – E input Statements (S STM): n n Claus Brabrand, UFPE, Brazil S : | | skip ; | v : = E ; | output E ; if E then S else S’ while E do S | { var v; S 1 … Sn } (…assume we only have integer variables ‘x’, ‘y’, ‘z’) DATA-FLOW ANALYSIS [ 14 ] Aug 11, 2010

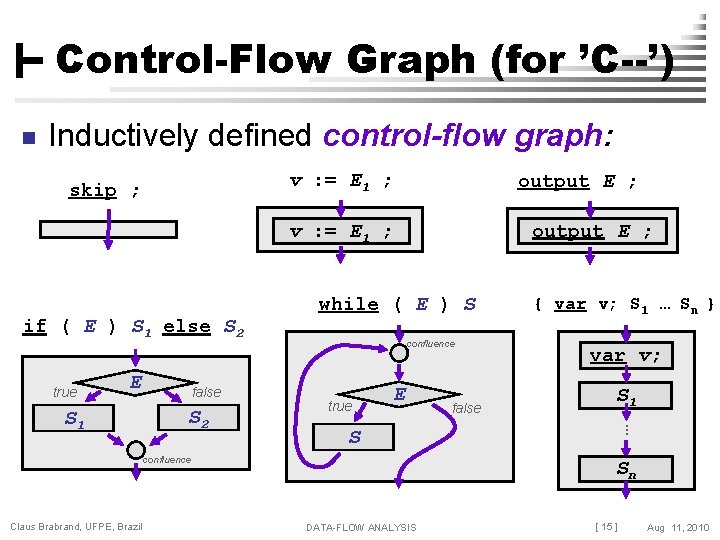
Control-Flow Graph (for ’C--’) n Inductively defined control-flow graph: v : = E 1 ; skip ; output E ; v : = E 1 ; output E ; while ( E ) S if ( E ) S 1 else S 2 true E S 1 S confluence Claus Brabrand, UFPE, Brazil false var v; … S 1 false confluence { var v; S 1 … Sn } Sn DATA-FLOW ANALYSIS [ 15 ] Aug 11, 2010

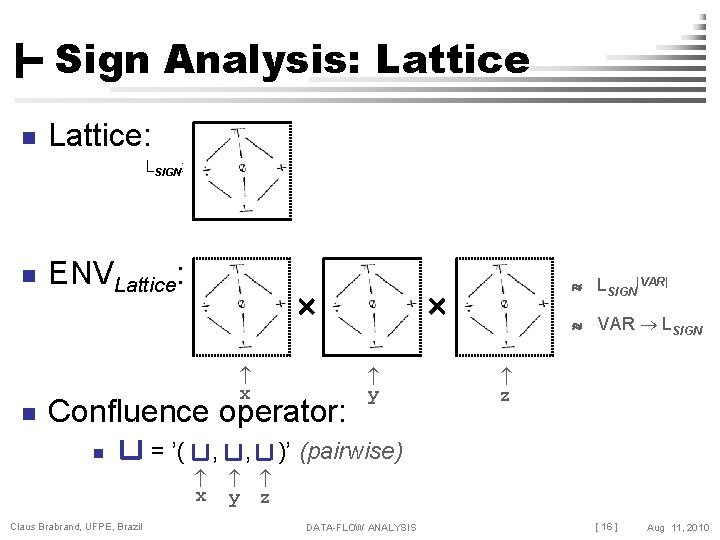
Sign Analysis: Lattice n Lattice: LSIGN: n n ENVLattice: Confluence operator: n = ’( , x Claus Brabrand, UFPE, Brazil x , LSIGN|VAR| y VAR LSIGN z )’ (pairwise) y z DATA-FLOW ANALYSIS [ 16 ] Aug 11, 2010

Sign Analysis: Transfer F’s n Transfer Functions: Env[x ] Env[x sign(Env, Exp)] Claus Brabrand, UFPE, Brazil var x; output … ; x : = Exp ; DATA-FLOW ANALYSIS [ 17 ] Aug 11, 2010

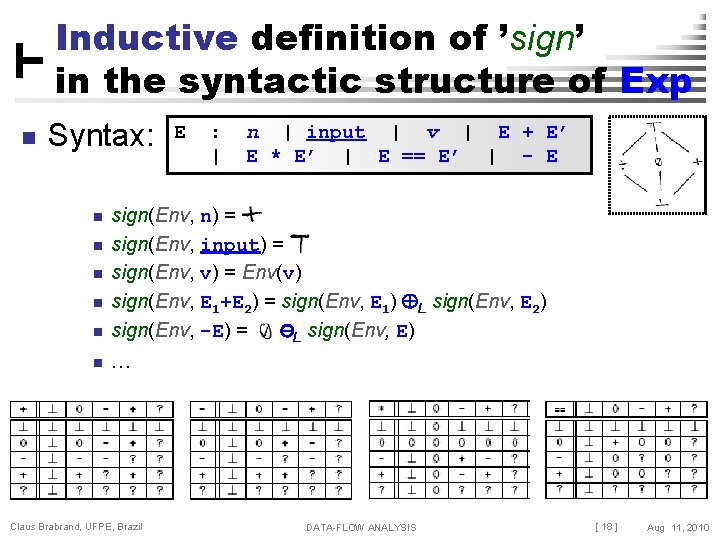
Inductive definition of ’sign’ in the syntactic structure of Exp n Syntax: E : | n | input | v | E + E’ E * E’ | E == E’ | - E n sign(Env, n) = sign(Env, input) = sign(Env, v) = Env(v) sign(Env, E 1+E 2) = sign(Env, E 1) L sign(Env, E 2) sign(Env, -E) = -L sign(Env, E) n … n n Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 18 ] Aug 11, 2010

Exercise: n n n Come up with a program the analysis… A) n can analyse precisely n can’t analyse precisely B) Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 19 ] Aug 11, 2010

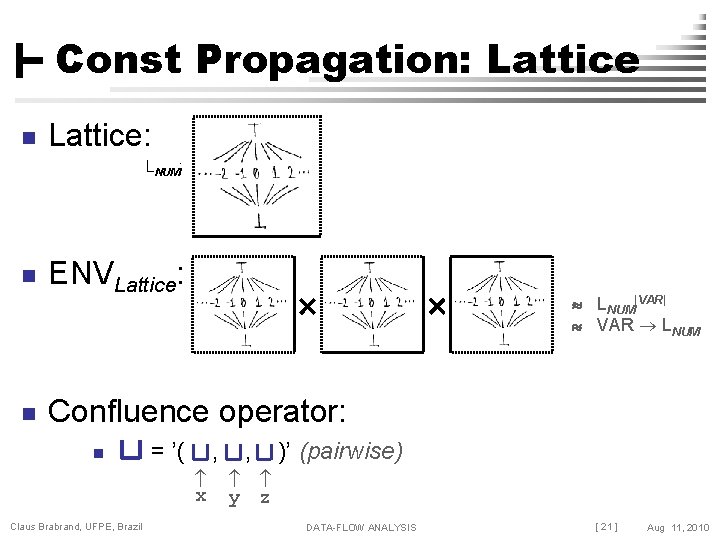
Const Propagation: Lattice n Lattice: LNUM: n n ENVLattice: LNUM|VAR| VAR LNUM Confluence operator: n = ’( , x Claus Brabrand, UFPE, Brazil , )’ (pairwise) y z DATA-FLOW ANALYSIS [ 21 ] Aug 11, 2010

Const Propagation: Transfer F’s n Transfer Functions: Env[x ] Env[x eval(Env, Exp)] Claus Brabrand, UFPE, Brazil var x; output … ; x : = Exp ; DATA-FLOW ANALYSIS [ 22 ] Aug 11, 2010

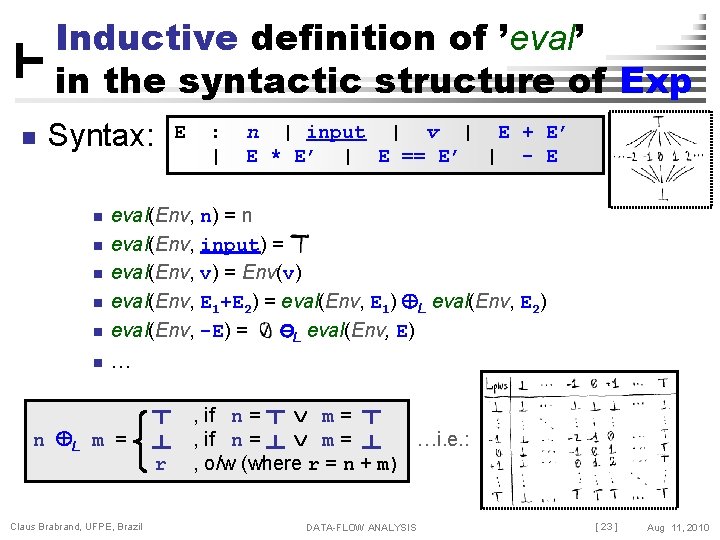
Inductive definition of ’eval’ in the syntactic structure of Exp n Syntax: E : | n | input | v | E + E’ E * E’ | E == E’ | - E n eval(Env, n) = n eval(Env, input) = eval(Env, v) = Env(v) eval(Env, E 1+E 2) = eval(Env, E 1) L eval(Env, E 2) eval(Env, -E) = -L eval(Env, E) n … n n n L m = Claus Brabrand, UFPE, Brazil r , if n = m= …i. e. : , o/w (where r = n + m) DATA-FLOW ANALYSIS [ 23 ] Aug 11, 2010

Exercise: n n n Come up with a program the analysis… A) n can analyse precisely n can’t analyse precisely B) Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 24 ] Aug 11, 2010

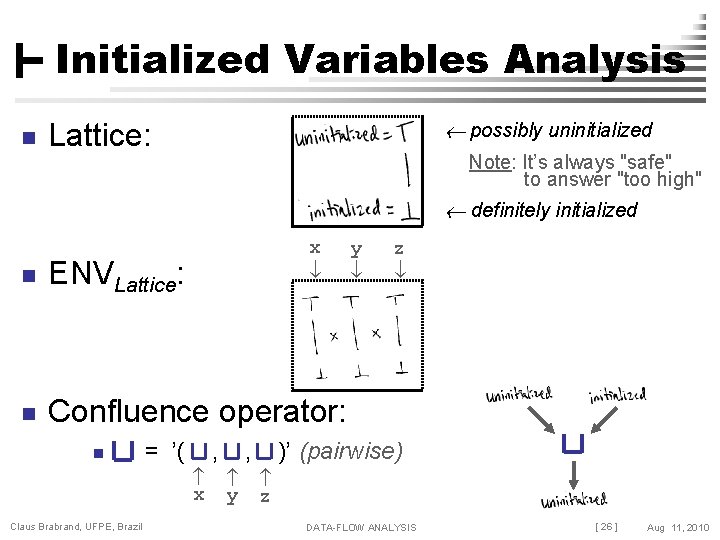
Initialized Variables Analysis n possibly uninitialized Lattice: Note: It’s always "safe" to answer "too high" definitely initialized x n ENVLattice: n Confluence operator: n = ’( , x Claus Brabrand, UFPE, Brazil , y z )’ (pairwise) y z DATA-FLOW ANALYSIS [ 26 ] Aug 11, 2010

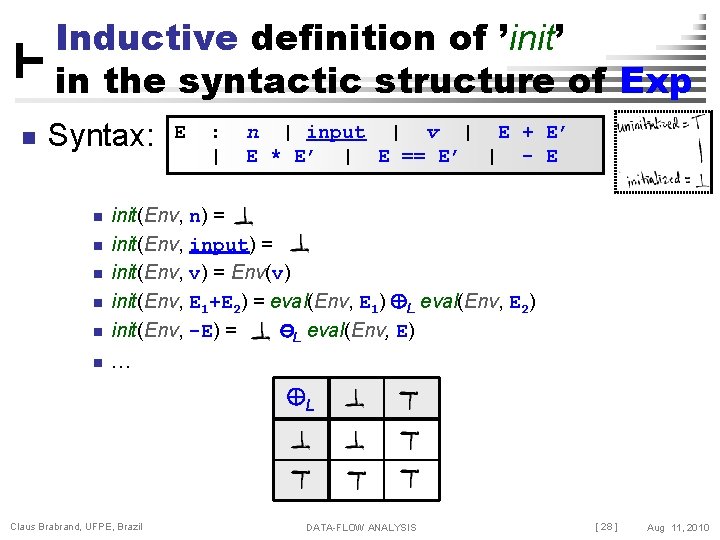
Initialized Variables Analysis n Transfer Functions: Env[x ] Env[x init(Env, Exp)] Claus Brabrand, UFPE, Brazil var x; output … ; x : = … ; DATA-FLOW ANALYSIS [ 27 ] Aug 11, 2010

Inductive definition of ’init’ in the syntactic structure of Exp n Syntax: E : | n | input | v | E + E’ E * E’ | E == E’ | - E n init(Env, n) = init(Env, input) = init(Env, v) = Env(v) init(Env, E 1+E 2) = eval(Env, E 1) L eval(Env, E 2) init(Env, -E) = -L eval(Env, E) n … n n L Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 28 ] Aug 11, 2010

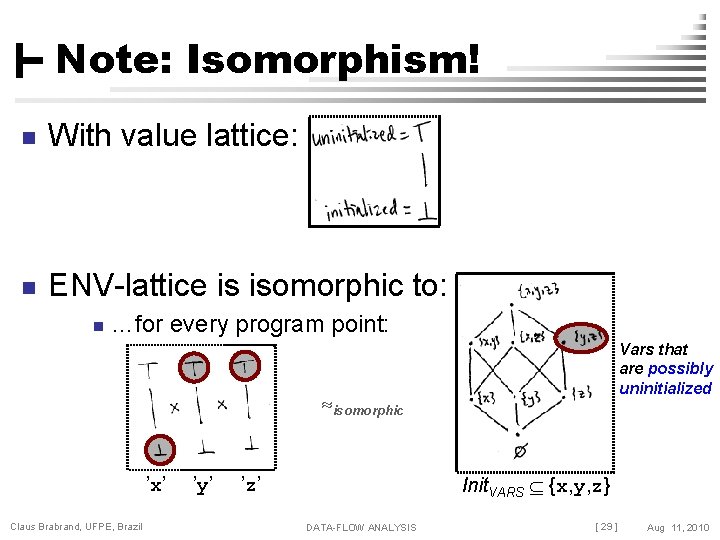
Note: Isomorphism! n With value lattice: n ENV-lattice is isomorphic to: n …for every program point: Vars that are possibly uninitialized isomorphic ’x’ Claus Brabrand, UFPE, Brazil ’y’ Init. VARS {x, y, z} ’z’ DATA-FLOW ANALYSIS [ 29 ] Aug 11, 2010

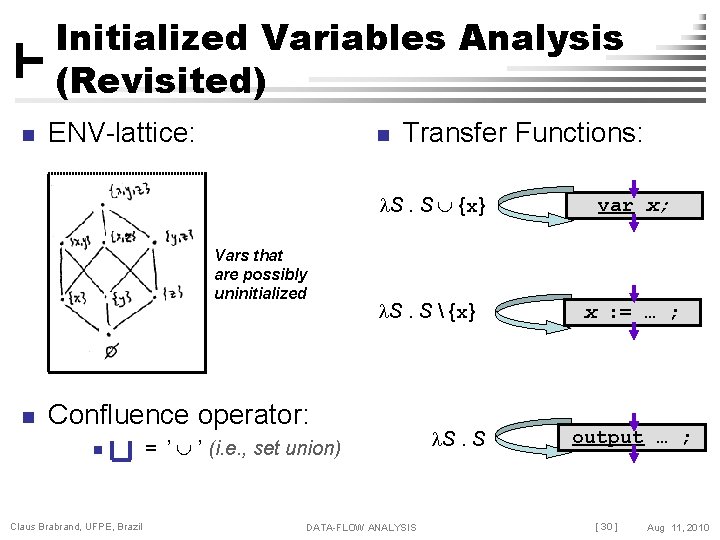
Initialized Variables Analysis (Revisited) n ENV-lattice: n Vars that are possibly uninitialized n Transfer Functions: S. S {x} var x; S. S {x} x : = … ; Confluence operator: n Claus Brabrand, UFPE, Brazil = ’ ’ (i. e. , set union) DATA-FLOW ANALYSIS S. S output … ; [ 30 ] Aug 11, 2010

Exercise: n n n Come up with a program the analysis… A) n can analyse precisely n can’t analyse precisely B) Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 31 ] Aug 11, 2010

Set-based analyses… {may, must} {forwards, backwards} Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS Aug 11, 2010

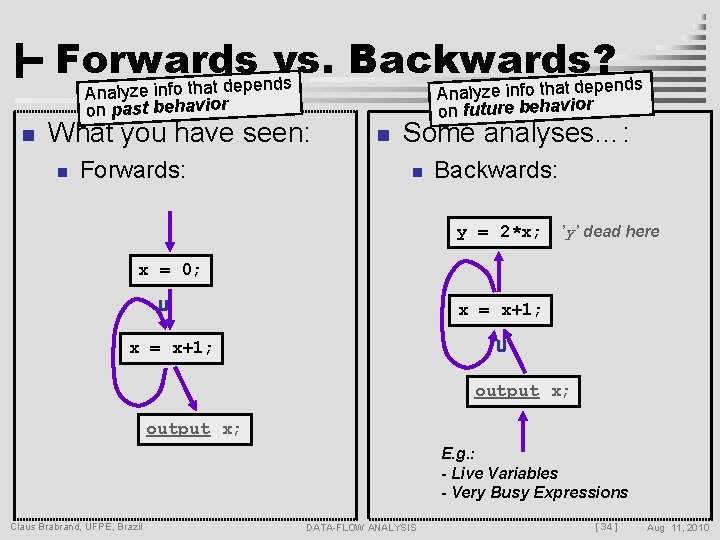
Forwards vs. Backwards? depends Analyze info that on past behavior n What you have seen: n Forwards: Analyze info that d on future behavior n Some analyses…: n Backwards: y = 2*x; ’y’ dead here x = 0; x = x+1; output x; E. g. : - Live Variables - Very Busy Expressions Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 34 ] Aug 11, 2010

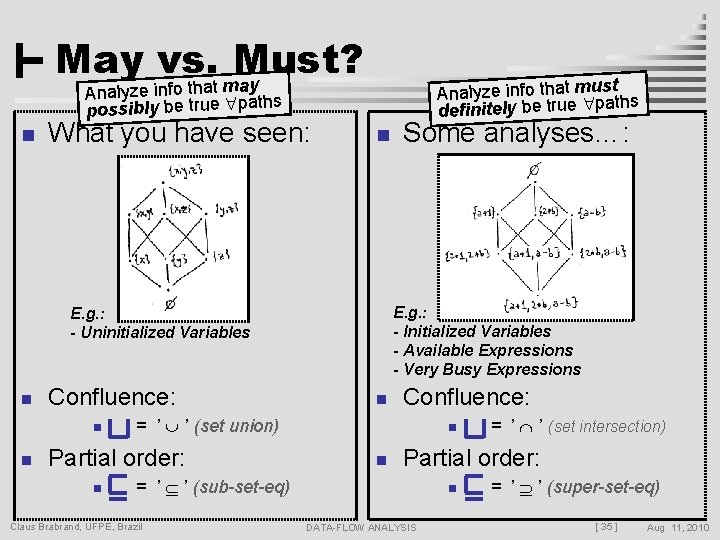
May vs. m. Must? ay t Analyze info that mupsaths definitely be true Analyze info that s possibly be true path n What you have seen: n E. g. : - Initialized Variables - Available Expressions - Very Busy Expressions E. g. : - Uninitialized Variables n Confluence: n n n Confluence: = ’ ’ (set union) Partial order: n Some analyses…: n n Partial order: = ’ ’ (sub-set-eq) Claus Brabrand, UFPE, Brazil = ’ ’ (set intersection) n DATA-FLOW ANALYSIS = ’ ’ (super-set-eq) [ 35 ] Aug 11, 2010

WORKSHOP n Reaching Definitions: n n Live Variables: n n ' ' (backward), ' ' (may / smallest set) Available Expressions: n n ' ' (forward), ' ' (may / smallest set) ' ' (forward), ' ' (must / largest set) Very Busy Expressions: n ' ' (backward), ' ' (must / largest set) Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 39 ] Aug 11, 2010

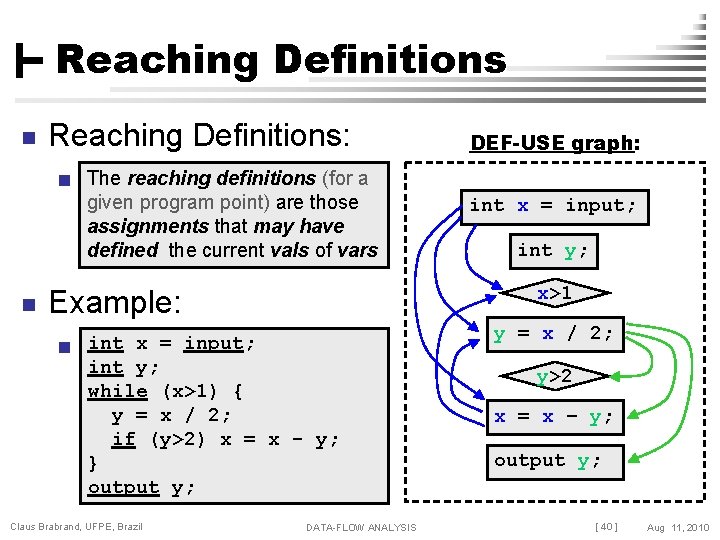
Reaching Definitions n Reaching Definitions: DEF-USE graph: n The reaching definitions (for a given program point) are those assignments that may have defined the current vals of vars n int y; x>1 Example: n int x = input; int y; while (x>1) { y = x / 2; if (y>2) x = x - y; } output y; Claus Brabrand, UFPE, Brazil int x = input; DATA-FLOW ANALYSIS y = x / 2; y>2 x = x – y; output y; [ 40 ] Aug 11, 2010

WHY do we do this? ”Learning takes place through the active behavior of the student: it is what (s)he does that (s)he learns, not what the teacher does. ” -- Ralph W. Tyler (1949) Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 41 ] Aug 11, 2010

WORKSHOP n n n 1) Define the problem 2) Show that the problem is undecidable 3) Define a Lattice n n 4) Define monotone transfer functions n n n Check that they are monotone (and explain how) 5) Pick a program the analysis can analyze n n Check that it is a lattice (and explain how) Make a "The Entire Process” diagram (cf. slide #5) 6) Repeat 5) for program the analysis can’t… 7) Explain possible uses of the analysis Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS [ 42 ] Aug 11, 2010

Now, please: 3’ recap n Please spend 3' on thinking about and writing down the main ideas and points from the lecture – now!: Immediately After 1 day After 1 week After 2 weeks Claus Brabrand, UFPE, Brazil DATA-FLOW ANALYSIS After 3 weeks [ 43 ] Aug 11, 2010