Data Engineering SQL Query Processing Shivnath Babu SQL

Data Engineering SQL Query Processing Shivnath Babu

SQL: Declarative Big Data Processing Let Developers Create and Run Spark Programs Faster: • Write less code • Read less data • Let the optimizer do the hard work 2

Write Less Code: Compute an Average private Int. Writable one = new Int. Writable(1) private Int. Writable output = new Int. Writable() proctected void map( Long. Writable key, Text value, Context context) { String[] fields = value. split("t") output. set(Integer. parse. Int(fields[1]) ) context. write(one, output) } Using RDDs data = sc. text. File(. . . ). split("t") data. map(lambda x: (x[0], [int(x[1]), 1])) . reduce. By. Key(lambda x, y: [x[0] + y[0], x[1] + y[1]]) . map(lambda x: [x[0], x[1][0] / x[1][1]]) . collect() Int. Writable one = new Int. Writable(1) Double. Writable average = new Double. Writable() protected void reduce( Int. Writable key, Iterable<Int. Writable> values, Context context) { int sum = 0 int count = 0 for(Int. Writable value : values) { sum += value. get() count++ } average. set(sum / (double) count) context. Write(key, average) } Using SQL SELECT name, avg(age) FROM people GROUP BY name

Write Less Code: Compute an Average Using RDDs data = sc. text. File(. . . ). split("t") data. map(lambda x: (x[0], [int(x[1]), 1])) . reduce. By. Key(lambda x, y: [x[0] + y[0], x[1] + y[1]]) . map(lambda x: [x[0], x[1][0] / x[1][1]]) . collect() Using SQL SELECT name, avg(age) FROM people GROUP BY name 4

Spark Seamlessly Integrates SQL with a Full Programming Language Embedding in a full programming language allows composition with functions to develop complex programs zip. To. City = udf(lambda city: <custom logic here>) def add_demographics(events): u = sql. Ctx. table("users") events . join(u, events. user_id == u. user_id) . with. Column("city", zip. To. City(df. zip)) 5

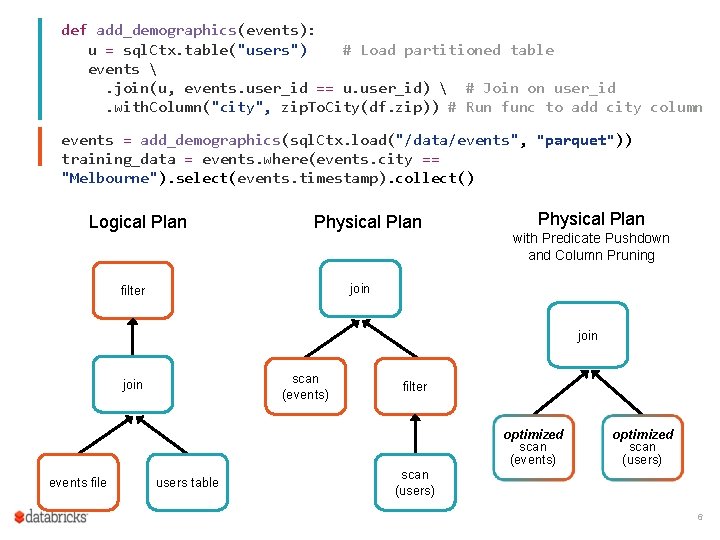
def add_demographics(events): u = sql. Ctx. table("users") # Load partitioned table events . join(u, events. user_id == u. user_id) # Join on user_id. with. Column("city", zip. To. City(df. zip)) # Run func to add city column events = add_demographics(sql. Ctx. load("/data/events", "parquet")) training_data = events. where(events. city == "Melbourne"). select(events. timestamp). collect() Logical Plan Physical Plan with Predicate Pushdown and Column Pruning join filter join scan (events) join filter optimized scan (events) events file users table optimized scan (users) 6

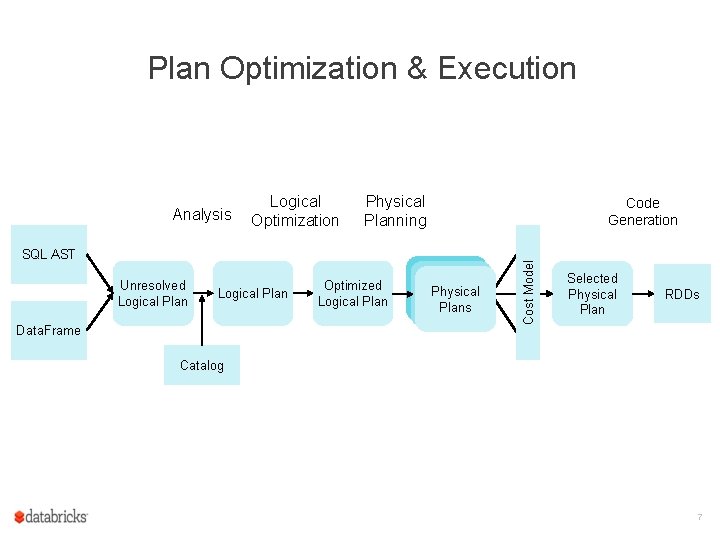
Plan Optimization & Execution Logical Optimization Physical Planning Code Generation SQL AST Unresolved Logical Plan Data. Frame Optimized Logical Plan Physical Plans Cost Model Analysis Selected Physical Plan RDDs Catalog 7

Query Processing Declarative SQL Query Plan

SQL Primer SPJ, or Select-Project-Join Queries Select <attribute list> From <relation list> Where <condition list> Example Filter Query over R(A, B, C): Select B From R Where R. A = “c” R. C > 10

SQL Primer (contd. ) SPJ, or Select-Project-Join-Queries Select <attribute list> From <relation list> Where <condition list> Example Join Query over R(A, B, C) and S(C, D, E): Select B, D From R, S Where R. A = “c” S. E = 2 R. C = S. C

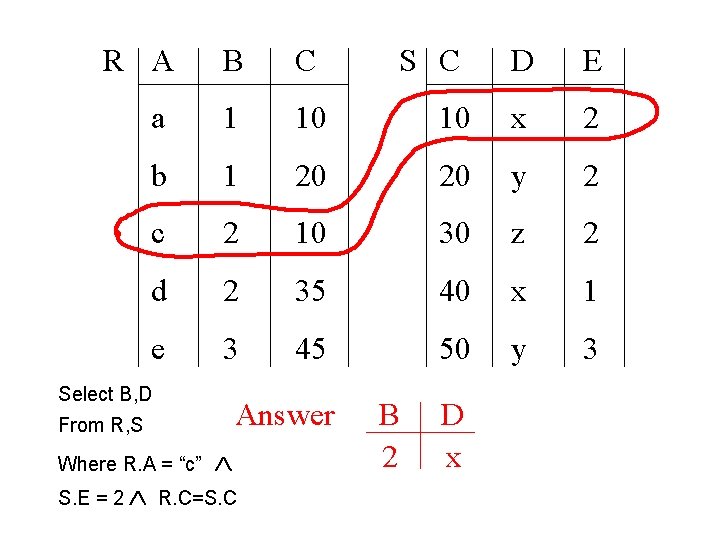
R A B C a 1 10 b 1 c D E 10 x 2 20 20 y 2 2 10 30 z 2 d 2 35 40 x 1 e 3 45 50 y 3 Select B, D Answer From R, S Where R. A = “c” S. E = 2 R. C=S. C S C B 2 D x

• How do we execute this query? Select B, D From R, S Where R. A = “c” S. E = 2 R. C=S. C One idea - Do Cartesian product - Select tuples - Do projection

RXS Select B, D From R, S Where R. A = “c” S. E = 2 R. C=S. C Bingo! Got one. . . R. A R. B R. C S. D S. E a 1 10 10 x 2 a. . 1 10 20 y 2 c. . 2 10 10 x 2

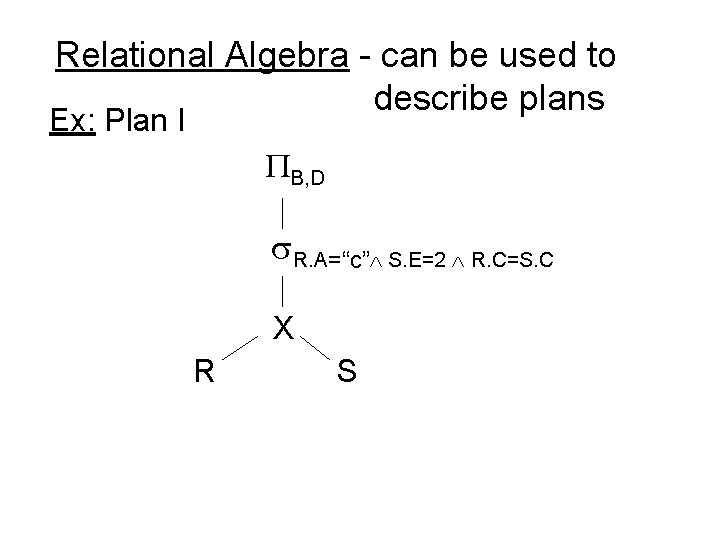
Relational Algebra - can be used to describe plans Ex: Plan I B, D R. A=“c” S. E=2 R. C=S. C X R S

Relational Algebra Primer Select: R. A=“c” R. C=10 Project: B, D Cartesian Product: R X S Natural Join: R S

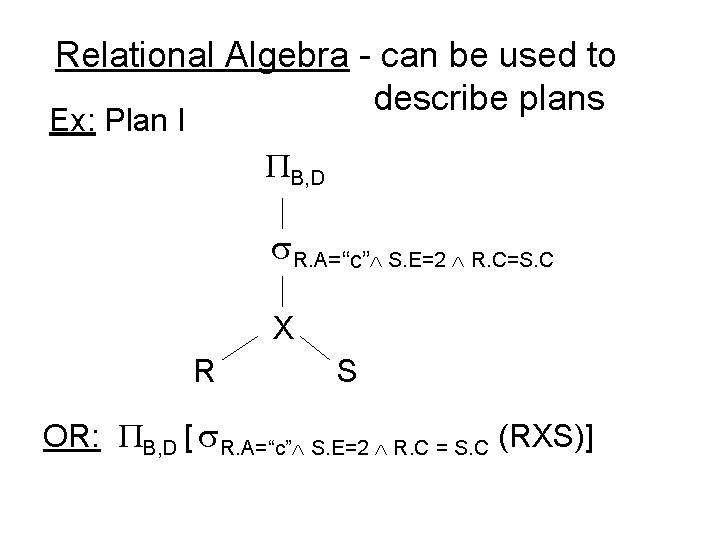
Relational Algebra - can be used to describe plans Ex: Plan I B, D R. A=“c” S. E=2 R. C=S. C X R S OR: B, D [ R. A=“c” S. E=2 R. C = S. C (RXS)]

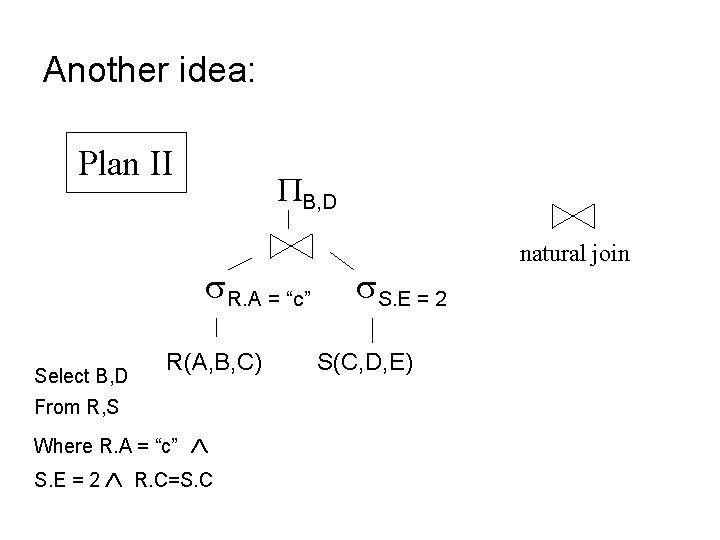
Another idea: Plan II B, D R. A = “c” Select B, D R(A, B, C) From R, S Where R. A = “c” S. E = 2 R. C=S. C S. E = 2 S(C, D, E) natural join

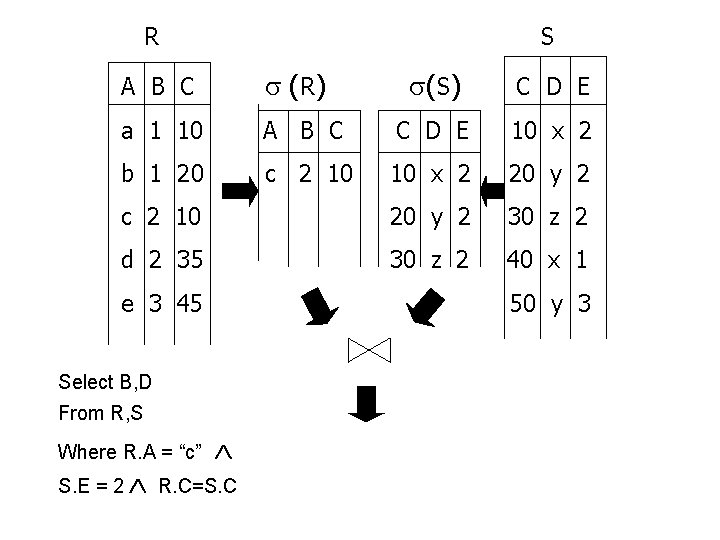
R S A B C ( R) (S) C D E a 1 10 A B C C D E 10 x 2 b 1 20 c 2 10 10 x 2 20 y 2 c 2 10 20 y 2 30 z 2 d 2 35 30 z 2 40 x 1 e 3 45 50 y 3 Select B, D From R, S Where R. A = “c” S. E = 2 R. C=S. C

Plan III Use R. A and S. C Indexes (1) Use R. A index to select R tuples with R. A = “c” (2) For each R. C value found, use S. C index to find matching tuples (3) Eliminate S tuples S. E 2 (4) Join matching R, S tuples, project B, D attributes, and place in result

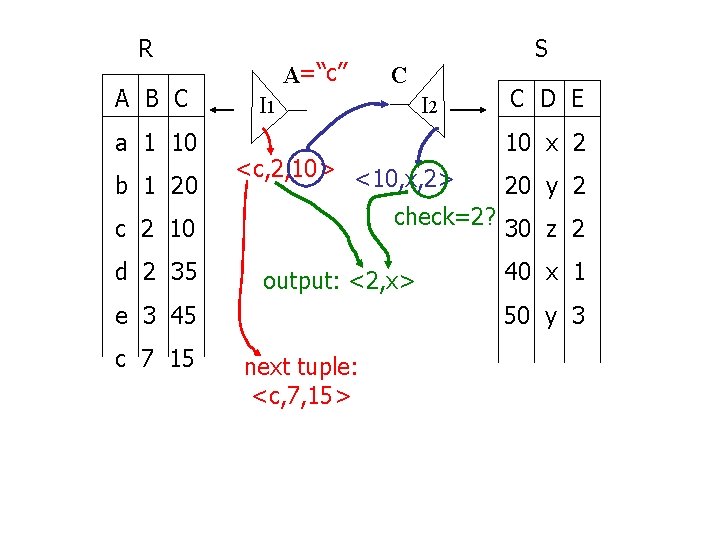
R A B C a 1 10 b 1 20 A=“c” I 2 <c, 2, 10> <10, x, 2> check=2? output: <2, x> e 3 45 c 7 15 C I 1 c 2 10 d 2 35 S C D E 10 x 2 20 y 2 30 z 2 40 x 1 50 y 3 next tuple: <c, 7, 15>

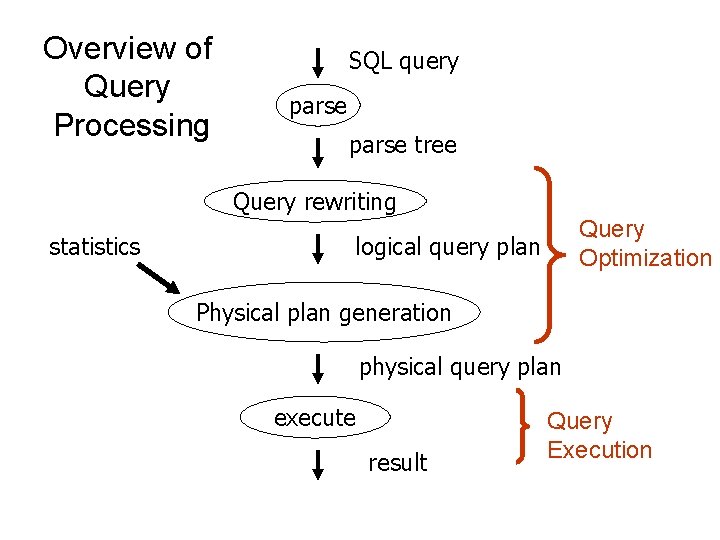
Overview of Query Processing SQL query parse tree Query rewriting statistics Query Optimization logical query plan Physical plan generation physical query plan execute result Query Execution

Example Query Select B, D From R, S Where R. A = “c” R. C=S. C

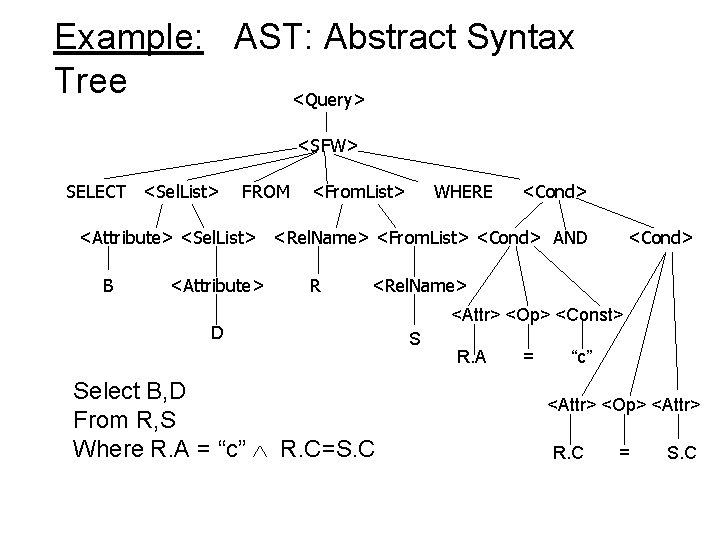
Example: AST: Abstract Syntax Tree <Query> <SFW> SELECT <Sel. List> FROM <From. List> WHERE <Cond> <Attribute> <Sel. List> <Rel. Name> <From. List> <Cond> AND B <Attribute> R <Cond> <Rel. Name> D Select B, D From R, S Where R. A = “c” R. C=S. C <Attr> <Op> <Const> S R. A = “c” <Attr> <Op> <Attr> R. C = S. C

Along with Parsing … • Semantic checks – Do the projected attributes exist in the relations in the From clause? – Ambiguous attributes? – Type checking, ex: R. A > 17. 5 • Expand views

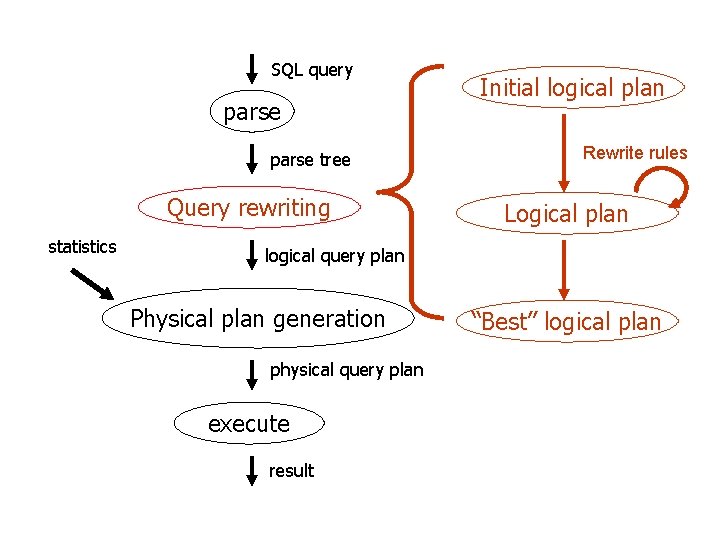
SQL query parse tree Query rewriting statistics Initial logical plan Rewrite rules Logical plan logical query plan Physical plan generation physical query plan execute result “Best” logical plan

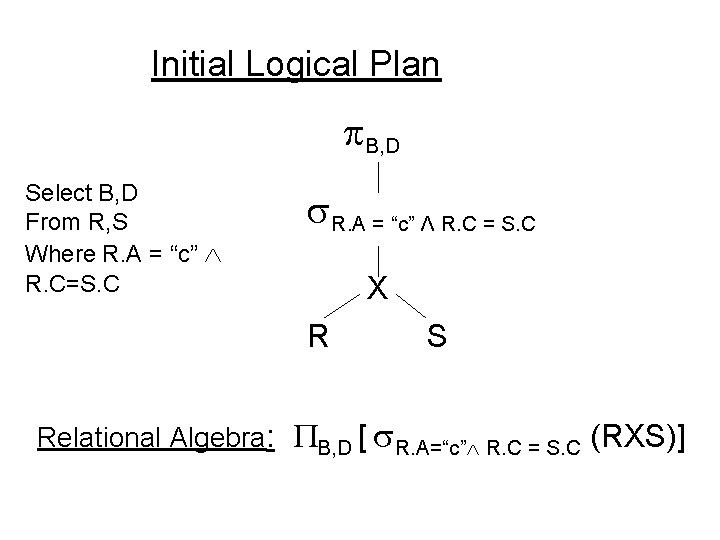
Initial Logical Plan B, D Select B, D From R, S Where R. A = “c” R. C=S. C R. A = “c” Λ R. C = S. C X R S Relational Algebra: B, D [ R. A=“c” R. C = S. C (RXS)]

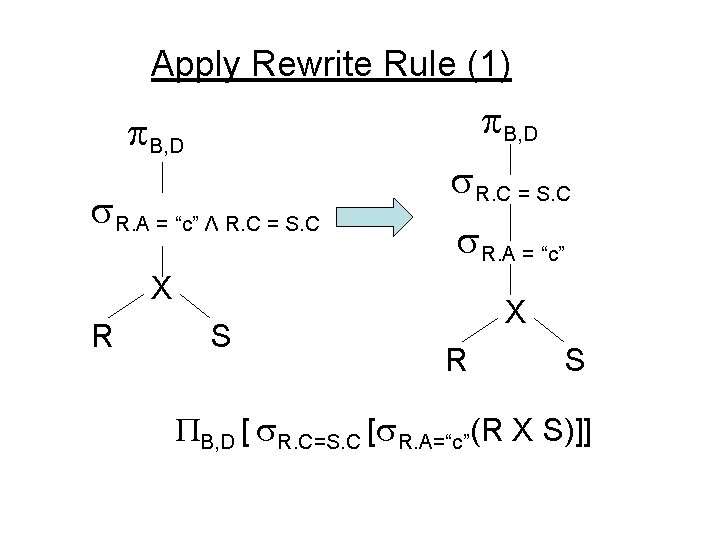
Apply Rewrite Rule (1) B, D R. A = “c” Λ R. C = S. C R. A = “c” X R S B, D [ R. C=S. C [ R. A=“c”(R X S)]]

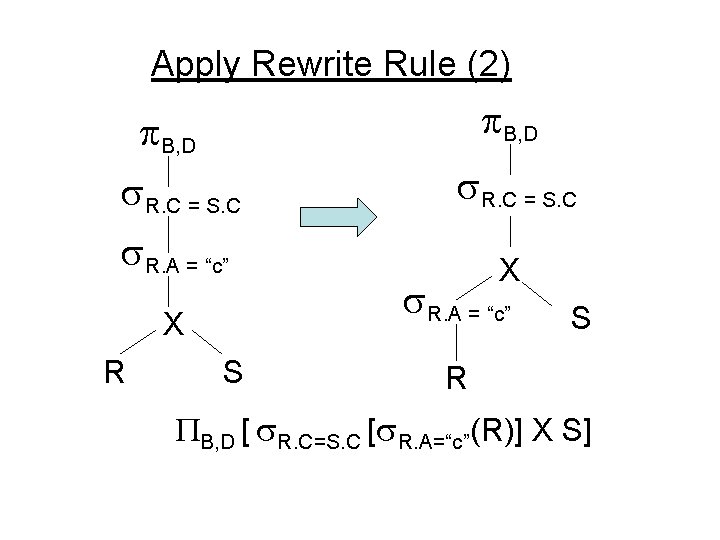
Apply Rewrite Rule (2) B, D R. C = S. C R. A = “c” X R S R. C = S. C X R. A = “c” S R B, D [ R. C=S. C [ R. A=“c”(R)] X S]

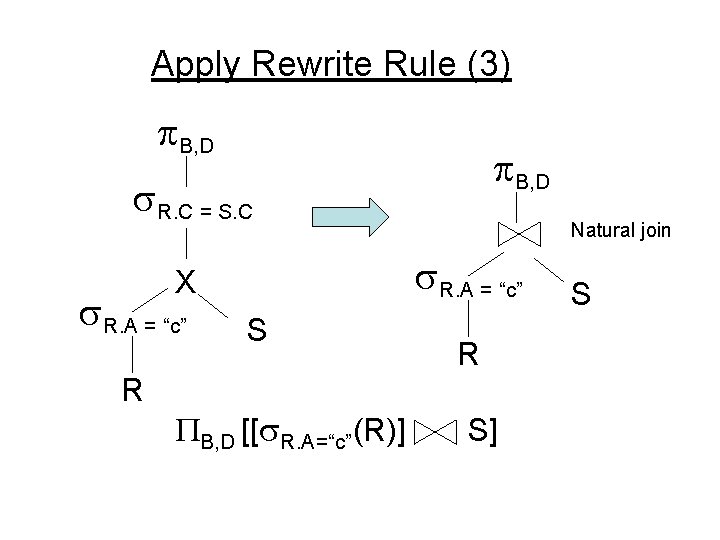
Apply Rewrite Rule (3) B, D R. C = S. C R. A = “c” X R. A = “c” R Natural join S B, D [[ R. A=“c”(R)] R S] S

Some Query Rewrite Rules • Transform one logical plan into another – Do not use statistics • • Equivalences in relational algebra Push-down predicates Do projects early Avoid cross-products if possible

Equivalences in Relational Algebra R (R S= S R Commutativity S) T=R (S T) Associativity Also holds for: Cross Products, Union, Intersection Rx. S=Sx. R (R x S) x T = R x (S x T) RUS=SUR R U (S U T) = (R U S) U T

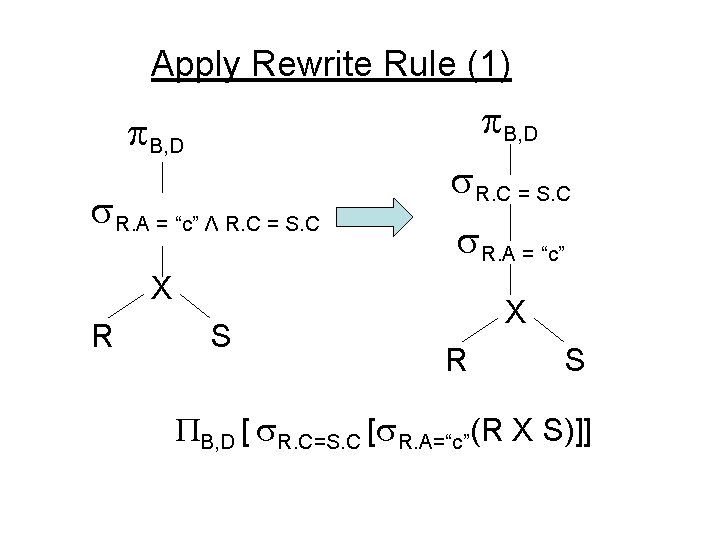
Apply Rewrite Rule (1) B, D R. A = “c” Λ R. C = S. C R. A = “c” X R S B, D [ R. C=S. C [ R. A=“c”(R X S)]]

Rules: Project Let: X = set of attributes Y = set of attributes XY = X U Y xy (R) = x [ y (R)]

Rules: + combined Let p = predicate with only R attribs q = predicate with only S attribs m = predicate with only R, S attribs p (R S) = q (R S) = [ R p (R)] [ S q (S)]

Rules: + combined (continued) p q (R S) = [ p (R)] [ q (S)] p q m (R S) = m [( p R) ( q S)] pvq (R S) = [( p R) S] U [R ( q S)]

Which are “good” transformations? p 1 p 2 (R) p 1 [ p 2 (R)] p (R S) [ p (R)] S R S S R x [ p (R)] x { p [ xz (R)]}

Conventional wisdom: do projects early Example: R(A, B, C, D, E) P: (A=3) (B=“cat”) E { p (R)} vs. E { p{ ABE(R)}}

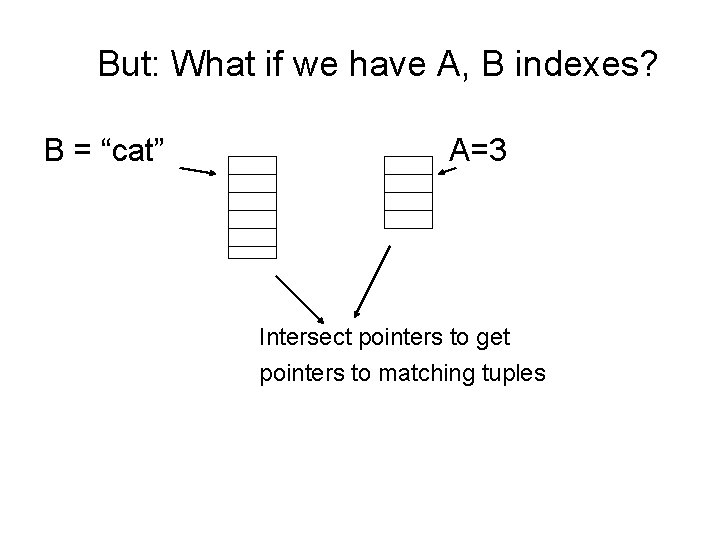
But: What if we have A, B indexes? B = “cat” A=3 Intersect pointers to get pointers to matching tuples

Bottom line: • No transformation is always good • Some are usually good: – Push selections down – Avoid cross-products if possible – Subqueries Joins

Avoid Cross Products (if possible) Select B, D From R, S, T, U Where R. A = S. B R. C=T. C R. D = U. D • Which join trees avoid cross-products? • If you can't avoid cross products, perform them as late as possible

More Query Rewrite Rules • Transform one logical plan into another – Do not use statistics • Equivalences in relational algebra • Push-down predicates • Do projects early • Avoid cross-products if possible • Use left-deep trees • Subqueries Joins • Use of constraints, e. g. , uniqueness

SQL query parse tree Query rewriting statistics Best logical query plan Physical plan generation Best physical query plan execute result

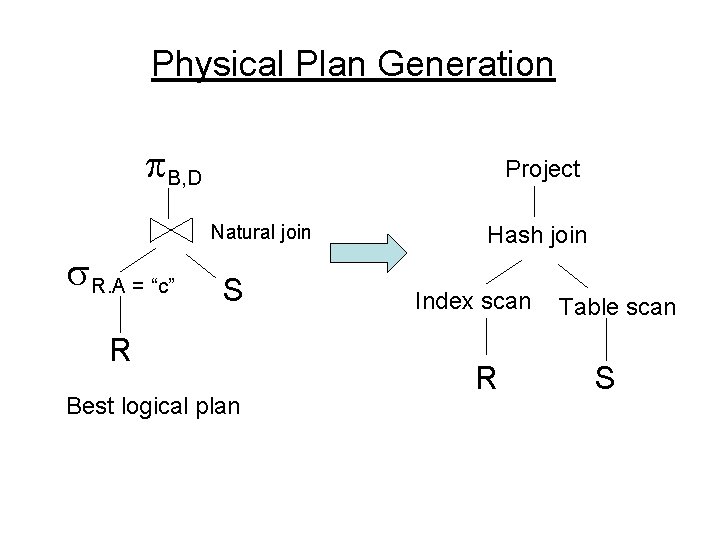
Physical Plan Generation B, D Project Natural join R. A = “c” S R Best logical plan Hash join Index scan R Table scan S

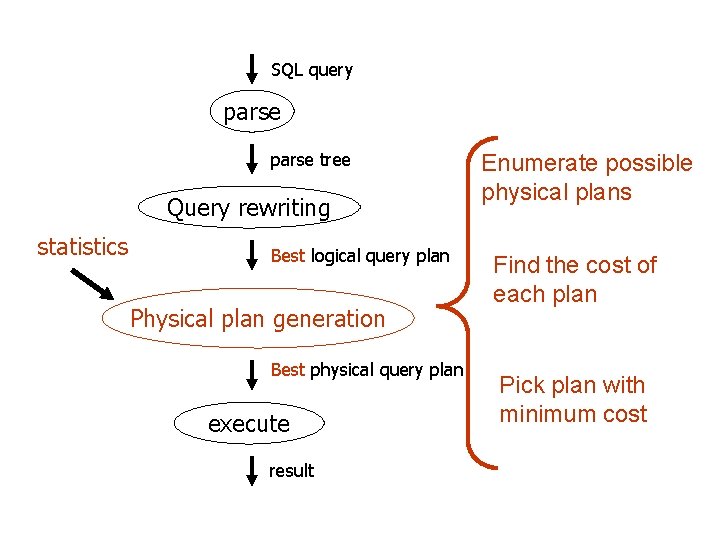
SQL query parse tree Query rewriting statistics Best logical query plan Physical plan generation Best physical query plan execute result Enumerate possible physical plans Find the cost of each plan Pick plan with minimum cost

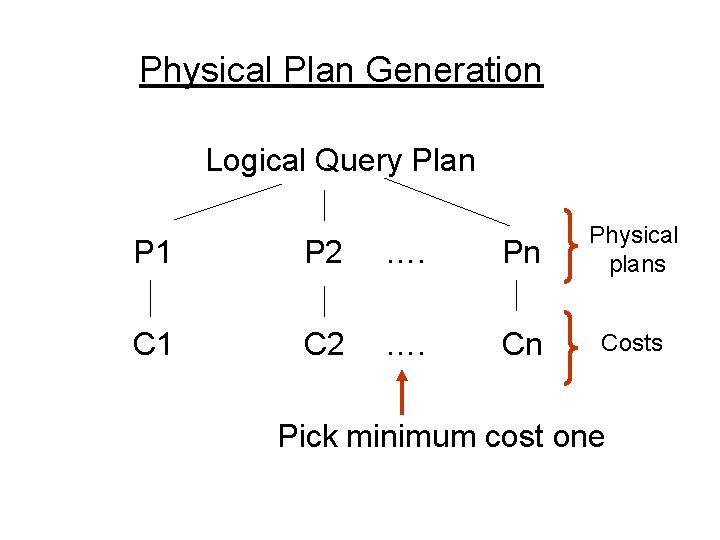
Physical Plan Generation Logical Query Plan P 1 P 2 …. Pn Physical plans C 1 C 2 …. Cn Costs Pick minimum cost one

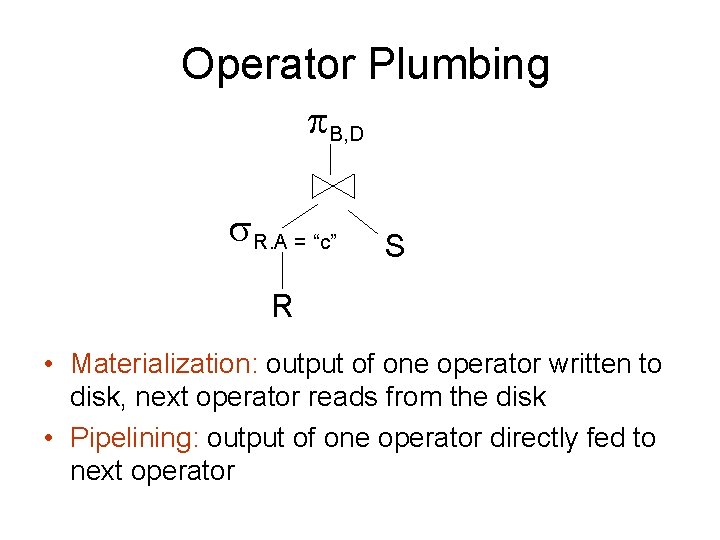
Operator Plumbing B, D R. A = “c” S R • Materialization: output of one operator written to disk, next operator reads from the disk • Pipelining: output of one operator directly fed to next operator

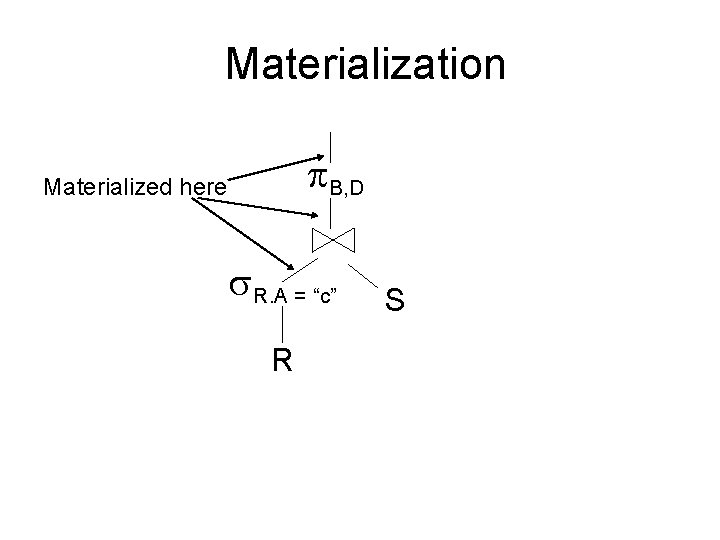
Materialization B, D Materialized here R. A = “c” R S

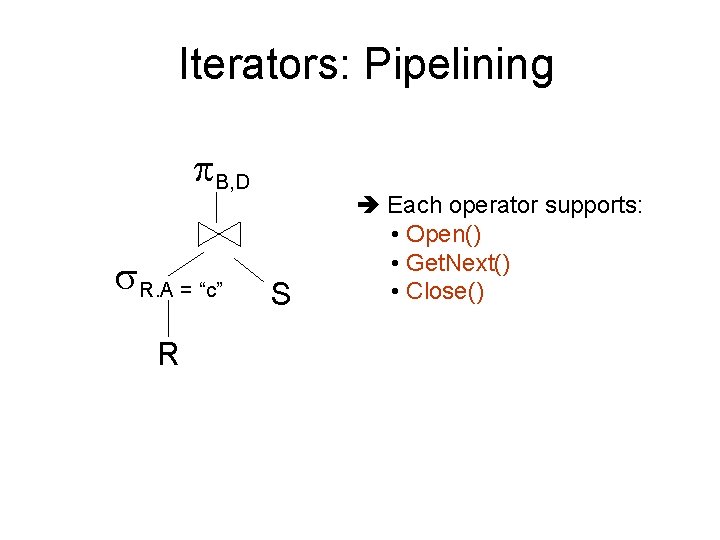
Iterators: Pipelining B, D R. A = “c” R S Each operator supports: • Open() • Get. Next() • Close()

Iterator for Table Scan (R) Open() { /** initialize variables */ b = first block of R; t = first tuple in block b; } Close() { /** nothing to be done */ } Get. Next() { IF (t is past last tuple in block b) { set b to next block; IF (there is no next block) /** no more tuples */ RETURN EOT; ELSE t = first tuple in b; } /** return current tuple */ oldt = t; set t to next tuple in block b; RETURN oldt; }

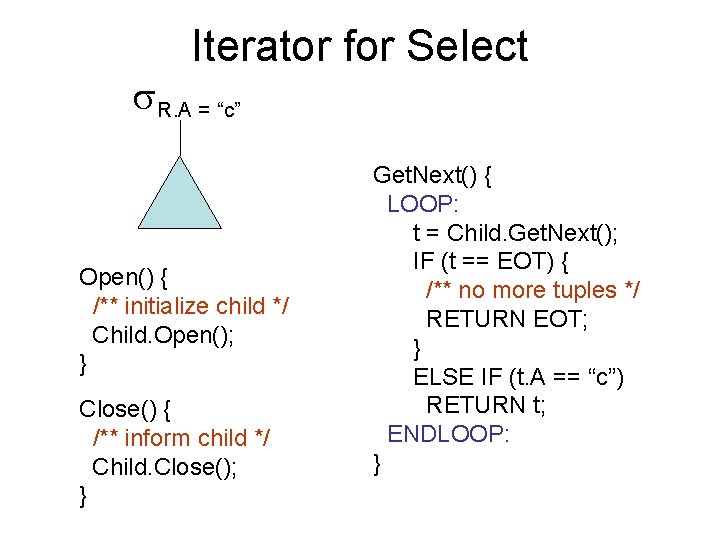
Iterator for Select R. A = “c” Open() { /** initialize child */ Child. Open(); } Close() { /** inform child */ Child. Close(); } Get. Next() { LOOP: t = Child. Get. Next(); IF (t == EOT) { /** no more tuples */ RETURN EOT; } ELSE IF (t. A == “c”) RETURN t; ENDLOOP: }

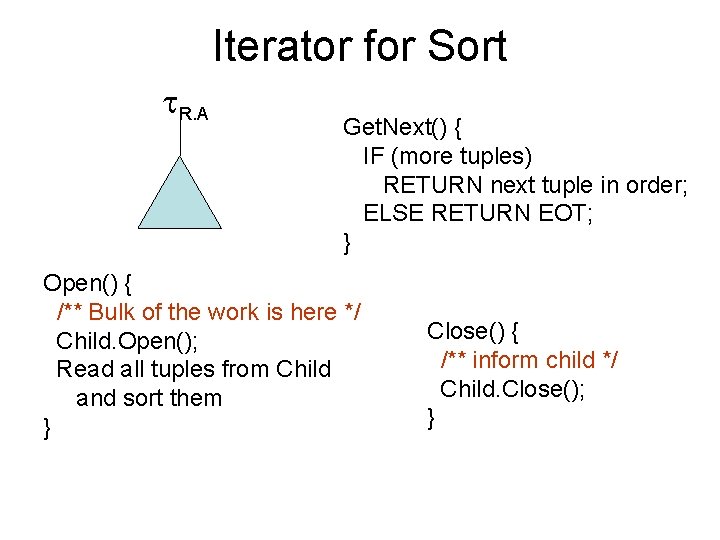
Iterator for Sort R. A Get. Next() { IF (more tuples) RETURN next tuple in order; ELSE RETURN EOT; } Open() { /** Bulk of the work is here */ Child. Open(); Read all tuples from Child and sort them } Close() { /** inform child */ Child. Close(); }

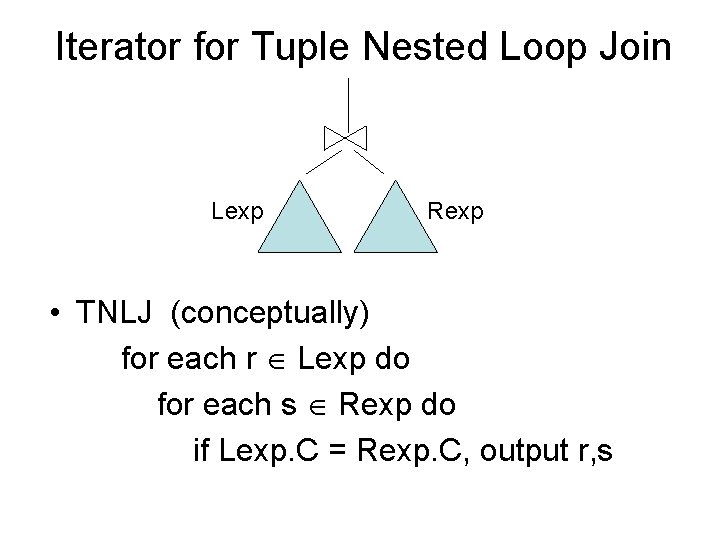
Iterator for Tuple Nested Loop Join Lexp Rexp • TNLJ (conceptually) for each r Lexp do for each s Rexp do if Lexp. C = Rexp. C, output r, s

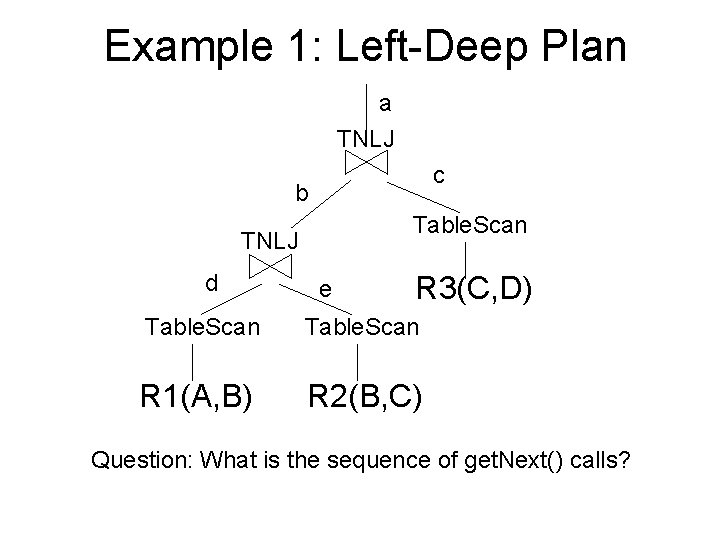
Example 1: Left-Deep Plan a TNLJ c b Table. Scan TNLJ d e R 3(C, D) Table. Scan R 1(A, B) R 2(B, C) Question: What is the sequence of get. Next() calls?

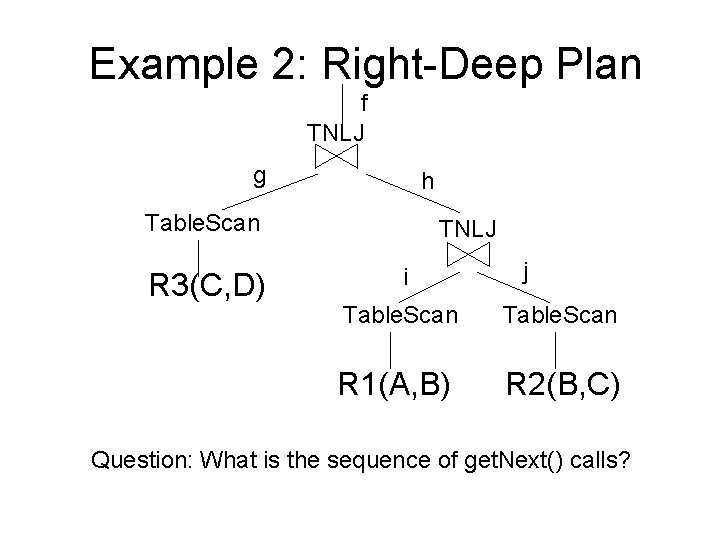
Example 2: Right-Deep Plan f TNLJ g h Table. Scan R 3(C, D) TNLJ i j Table. Scan R 1(A, B) R 2(B, C) Question: What is the sequence of get. Next() calls?

Cost Measure for a Physical Plan • There are many cost measures – Time to completion – Number of I/Os (we will see a lot of this) – Number of get. Next() calls • Tradeoff: Simplicity of estimation Vs. Accurate estimation of performance as seen by user