Data Encryption Standard In 1973 NIST published a

Data Encryption Standard § In 1973, NIST published a request for proposals for a national symmetric-key cryptosystem. § Walter Tuchman, an IBM researcher, refined LUCIFER and reduced the key size to 56 -bit, to fit on a chip. § In 1977, the results of Tuchman’s project of IBM was adopted as the DES by National Institute of Standards and Technology (NIST). § The DES is a symmetric-key block cipher and it uses a 56 bit key. Dr. K. Mani Analysis of Algorithms 1

… DES § DES is now considered insecure because a brute force attack is possible. § Cipher Detail: Key sizes: 56 bits, Block sizes: 64 bits, Structure: Feistel cipher. § As there are over 70, 000, 0 00, 000 (seventy quadrillion) possible keys of 56 bits, the feasibility of deriving a particular key in this way is extremely unlikely in typical threat environments. § Feistel cipher is a symmetric structure used in the construction of block ciphers. Dr. K. Mani Analysis of Algorithms 2
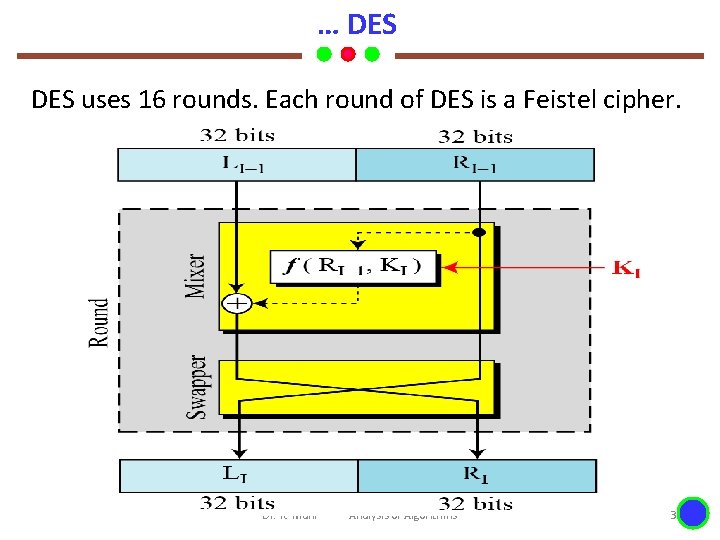
… DES uses 16 rounds. Each round of DES is a Feistel cipher. Dr. K. Mani Analysis of Algorithms 3
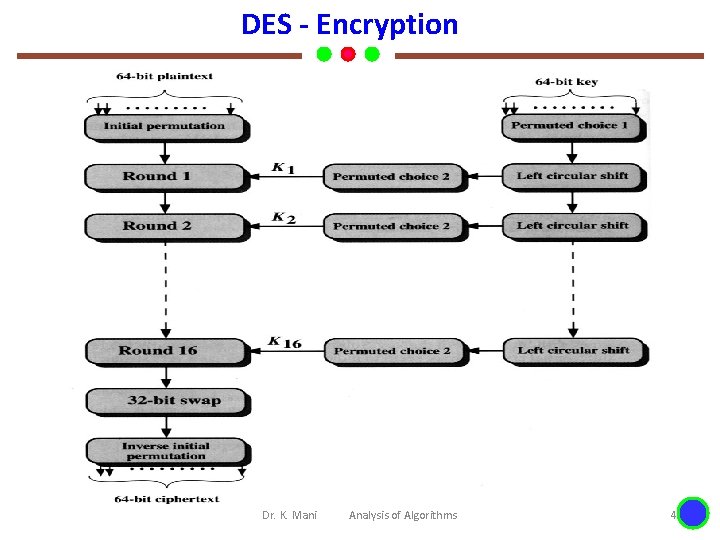
DES - Encryption Dr. K. Mani Analysis of Algorithms 4
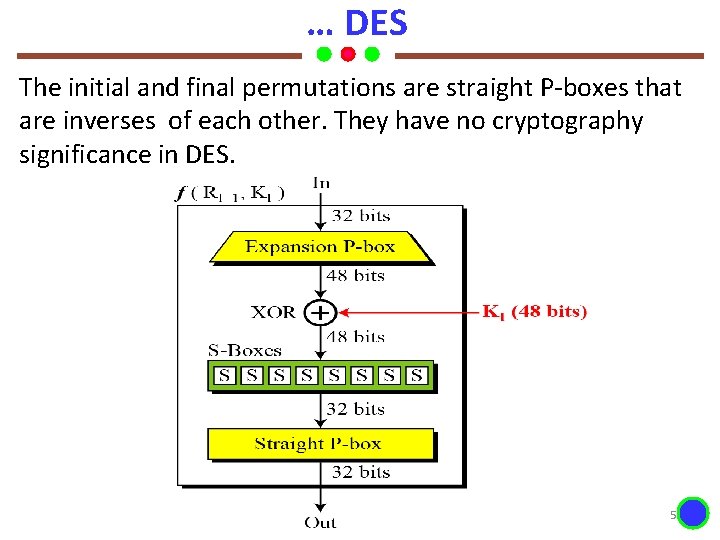
… DES The initial and final permutations are straight P-boxes that are inverses of each other. They have no cryptography significance in DES. Dr. K. Mani Analysis of Algorithms 5
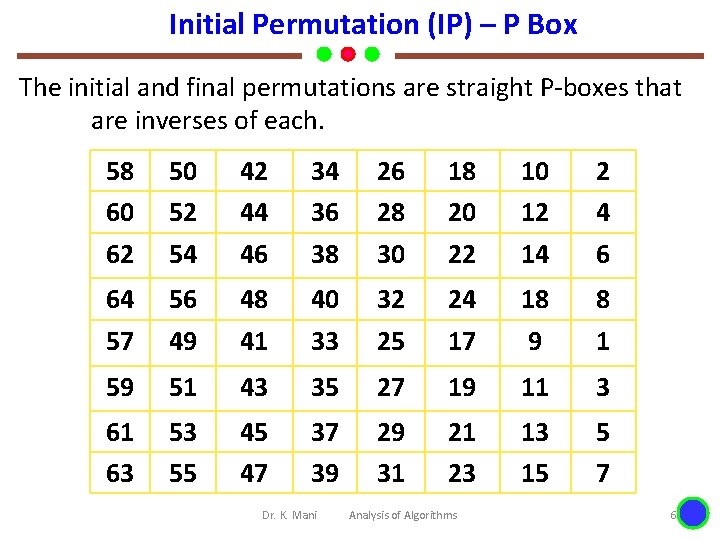
Initial Permutation (IP) – P Box The initial and final permutations are straight P-boxes that are inverses of each. 58 60 50 52 42 44 34 36 26 28 18 20 10 12 2 4 62 54 46 38 30 22 14 6 64 57 56 49 48 41 40 33 32 25 24 17 18 9 8 1 59 51 43 35 27 19 11 3 61 63 53 55 45 47 37 39 29 31 21 23 13 15 5 7 Dr. K. Mani Analysis of Algorithms 6
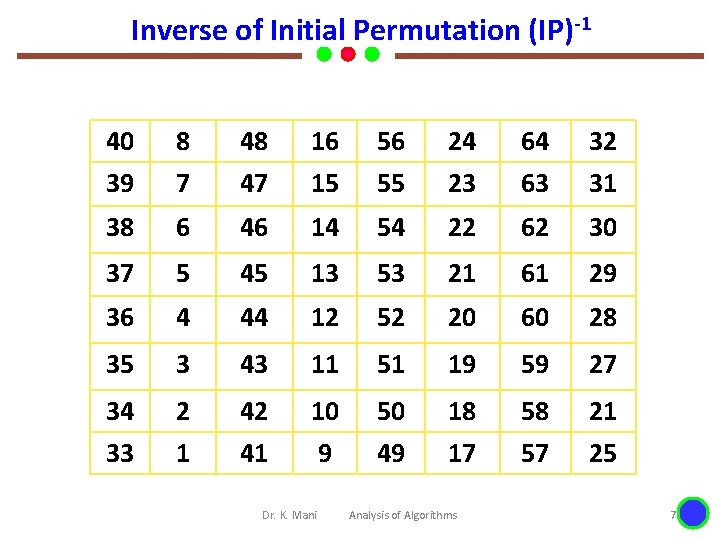
Inverse of Initial Permutation (IP)-1 40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31 38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29 36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 21 33 1 41 9 49 17 57 25 Dr. K. Mani Analysis of Algorithms 7
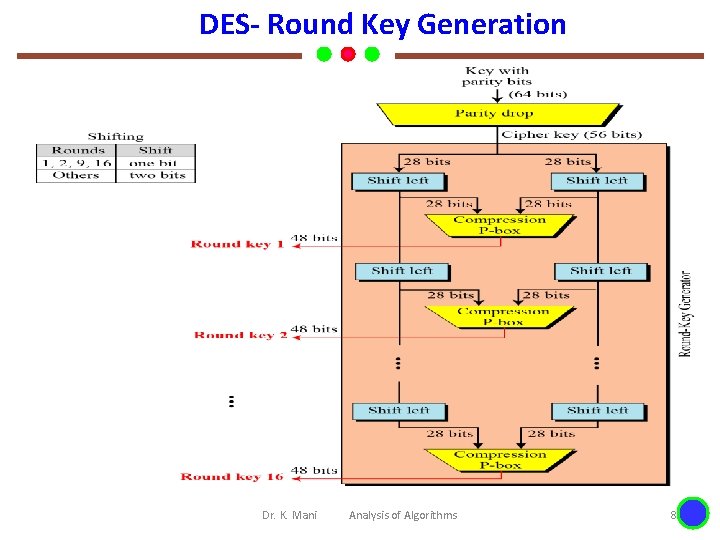
DES- Round Key Generation Dr. K. Mani Analysis of Algorithms 8

DES Key Schedule Calculation (a) Input Key 1 9 2 10 3 11 4 12 5 13 6 14 7 15 8 16 17 18 19 20 21 22 23 24 25 33 26 34 27 35 28 36 29 37 30 38 31 39 32 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Dr. K. Mani Analysis of Algorithms 9
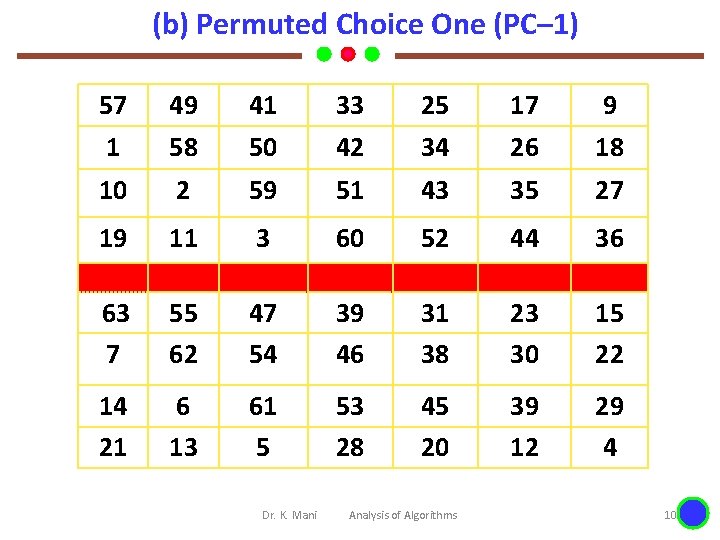
(b) Permuted Choice One (PC– 1) 57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 36 63 7 55 62 47 54 39 46 31 38 23 30 15 22 14 21 6 13 61 5 53 28 45 20 39 12 29 4 Dr. K. Mani Analysis of Algorithms 10
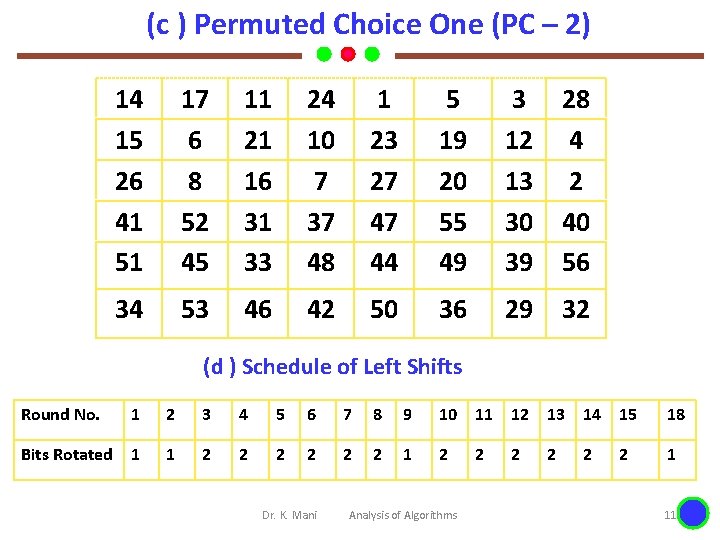
(c ) Permuted Choice One (PC – 2) 14 15 26 41 51 17 6 8 52 45 11 21 16 31 33 24 10 7 37 48 1 23 27 47 44 5 19 20 55 49 3 12 13 30 39 28 4 2 40 56 34 53 46 42 50 36 29 32 (d ) Schedule of Left Shifts Round No. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 Bits Rotated 1 1 2 2 2 1 2 1 Dr. K. Mani Analysis of Algorithms 2 2 2 11
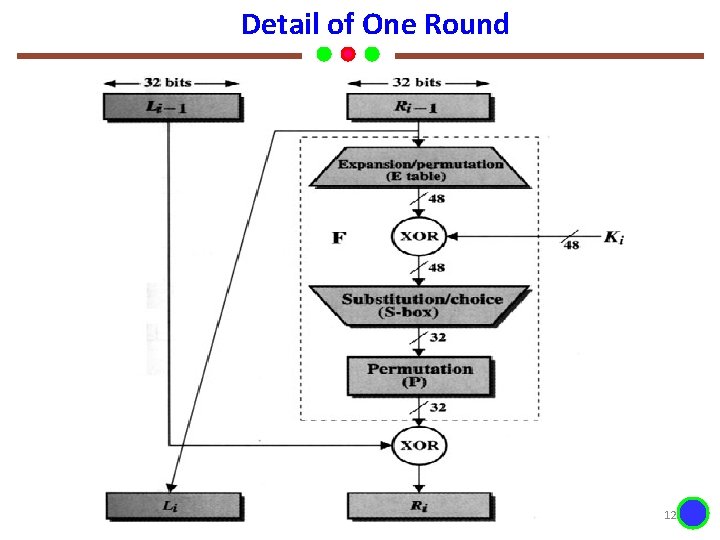
Detail of One Round Dr. K. Mani Analysis of Algorithms 12
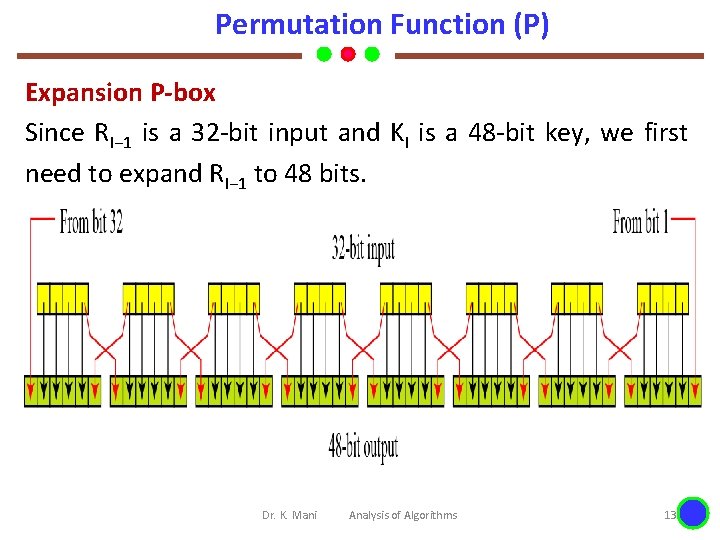
Permutation Function (P) Expansion P-box Since RI− 1 is a 32 -bit input and KI is a 48 -bit key, we first need to expand RI− 1 to 48 bits. Dr. K. Mani Analysis of Algorithms 13
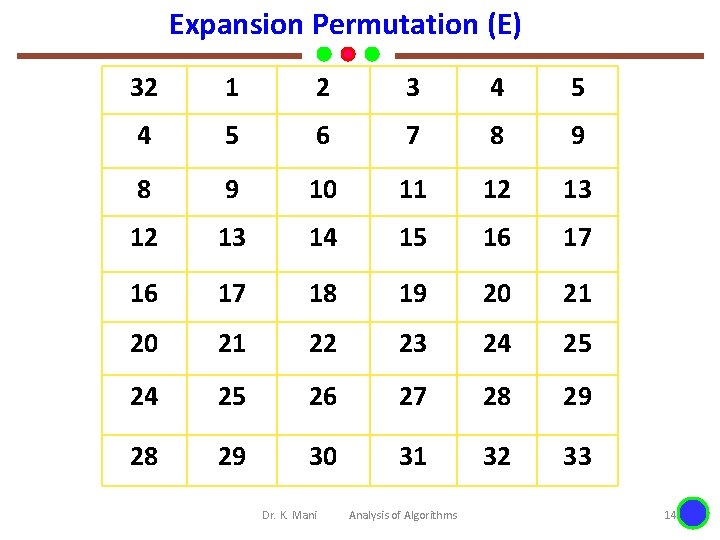
Expansion Permutation (E) 32 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Dr. K. Mani Analysis of Algorithms 14
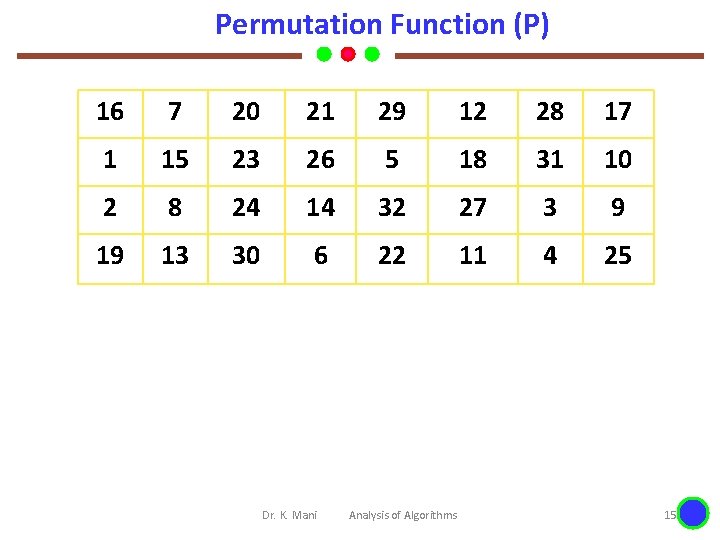
Permutation Function (P) 16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25 Dr. K. Mani Analysis of Algorithms 15
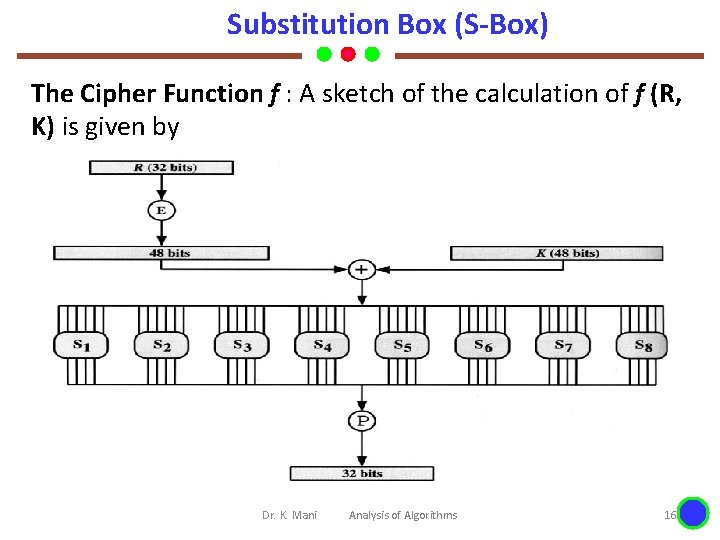
Substitution Box (S-Box) The Cipher Function f : A sketch of the calculation of f (R, K) is given by Dr. K. Mani Analysis of Algorithms 16
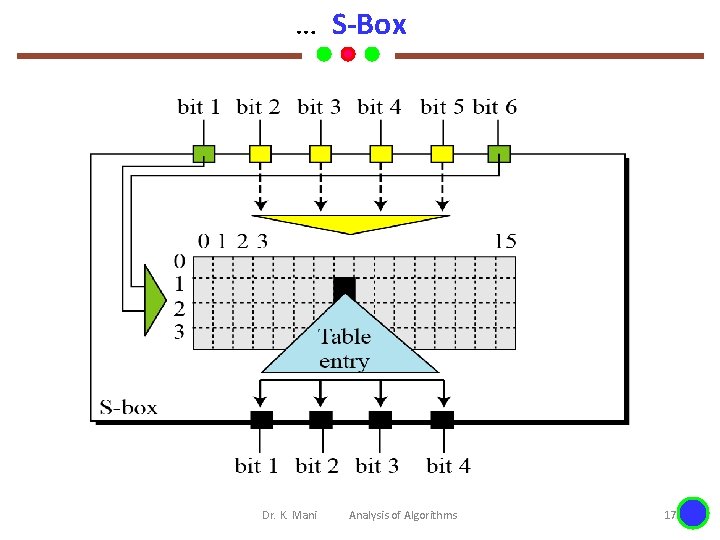
… S-Box Dr. K. Mani Analysis of Algorithms 17

DES S-Box s 1 0 14 4 2 3 13 1 1 0 15 7 2 4 1 3 15 12 8 4 2 5 6 7 15 11 8 8 3 9 10 11 12 13 14 15 10 6 12 5 9 0 7 4 14 2 13 1 14 8 13 6 2 11 15 12 9 7 4 1 7 14 10 0 2 9 10 6 5 12 11 9 11 3 3 5 3 8 10 5 0 6 13 For example, for input 011011 the row is 01, that is row 1, and the column is determined by 1101, that is column 13. In row 1 column 13 appears 5 so that the output is 0101. Dr. K. Mani Analysis of Algorithms 18
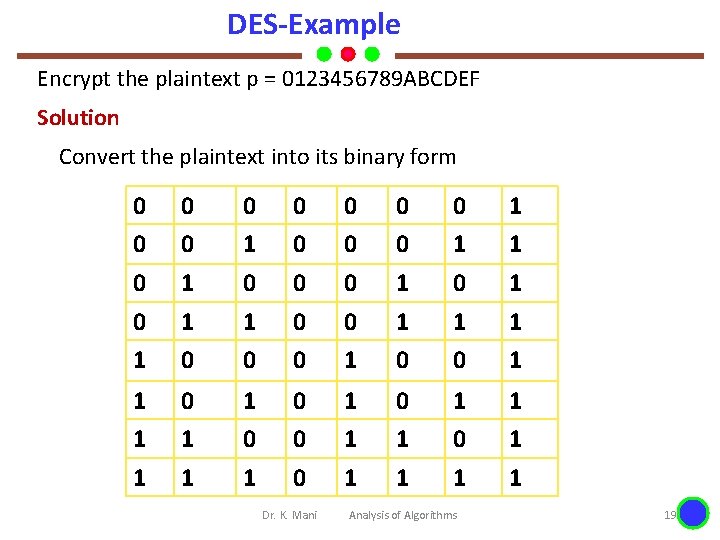
DES-Example Encrypt the plaintext p = 0123456789 ABCDEF Solution Convert the plaintext into its binary form 0 0 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 1 1 Dr. K. Mani Analysis of Algorithms 19

DES-Example The application of IP yields 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 So we obtain L 0 = 1100 0000 1100 1111 R 0 = 1111 0000 1010 Dr. K. Mani Analysis of Algorithms 20

DES-Key DES key property The sum of the eight bits of each byte is add i. e. , seven of the eight bits determine the value of the eighth bit e. g. , 133457799 BBCDFF 1 0 0 0 1 1 1 O 0 0 1 O 1 1 0 1 0 1 1 1 0 0 1 1 0 1 0 1 1 Dr. K. Mani Analysis of Algorithms 21

… DES-Key Using PC-1 table, C 0 and Do are computed as C 0 = 1111 0000 1100 1010 1111 D 0= 0101 0110 0111 1000 1111 Dr. K. Mani Analysis of Algorithms 22

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 23

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 24

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 25

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 26

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 27

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 28

Order of an Algorithm Dr. K. Mani Analysis of Algorithms 29
- Slides: 29