Data Encryption Chris Mraovich Overview Purpose of Encryption

Data Encryption Chris Mraovich

Overview • Purpose of Encryption • Permutations Bases and Factoradics • Project Summary

Purpose of Encryption

Protecting Digital Content • DVDs use CSS (Content Scramble System) • Weak Algorithm -Cracked by Jon Johansen in 1999

Protecting Digital Content Arcade Printed Circuit Boards • Capcom Play System 2 (CPS 2) -Used in mid 1990 s for 2 D games • Uses encryption on program ROM chips • Graphic ROM chips are not encrypted • Cracked by team

Protecting Digital Content Why use encryption on an arcade board? 1. ROM chips can be copied to a PC as binary data 2. Program can be written to interpret binary data 3. PC can then run the arcade without the board

Permutations, Bases, and Factoradics

Permutations Goal is to rearrange bits into a different pattern Original Form: 1 0 1 1 Encrypted Form: 1 1 0 1 Permutation – rearrangement of a set of objects

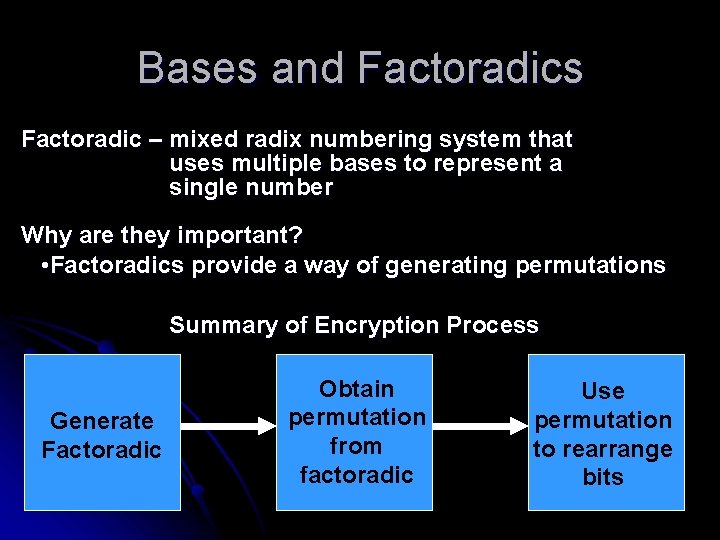
Bases and Factoradics Factoradic – mixed radix numbering system that uses multiple bases to represent a single number Why are they important? • Factoradics provide a way of generating permutations Summary of Encryption Process Generate Factoradic Obtain permutation from factoradic Use permutation to rearrange bits

Order & Total Permutations Order – number of objects (N) Total number of permutations for N objects is N! Suppose there are 4 objects N = 4, so there are 4! or 24 ways to rearrange 4 objects

Total Permutations of order 4 Int Factoradic Permutation 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 {0000} {0010} {0100} {0110} {0200} {0210} {1000} {1010} {1100} {1110} {1200} {1210} {2000} {2010} {2100} {2110} {2200} {2210} {3000} {3010} {3100} {3110} {3200} {3210} (0123) (0132) (0213) (0231) (0312) (0321) (1023) (1032) (1203) (1230) (1302) (1320) (2013) (2031) (2103) (2130) (2301) (2310) (3012) (3021) (3102) (3120) (3201) (3210) • Int is the base 10 representation of the factoradic • Each factoradic uniquely identifies a particular permutation • Walkthrough of how 2010 is converted to a permutation of order 4

Bases – Generate Factoradic Base 10 Base 2 20 10100 Write 2010 in Base 2 Multi-Base Factoradic 3100 24 2 3 2 2 2 1 2 0 (16) (8) 1 0 (4) (2) (1) 1 0 0 Expand the Binary Number (12 x 24) + (0 ( 2 x 23) + (1 ( 2 x 22) + (0 ( 2 x 21) + (0 ( 2 x 20) = 2010

From Base 2 to Factoradic Generalization of Base 2 Expansion ( 2 x 23) + (C ( 2 x 22) + (B ( 2 x 21) + (A ( 2 x 2 0) … (E 2 x 24) + (D A 2, B 2, C 2, D 2, E 2 are all numbers in base 2 (0 or 1) 2 n are powers of 2 What Changes : 1. ) The bases of A 2, B 2, C 2, D 2, E 2 increase from right to left 2. ) 2 n n! Factoradic Expansion ( 4 x 3!) + (C ( 3 x 2!) + (B ( 2 x 1!) + (A ( 1 x 0!) … (E 5 x 4!) + (D (Mixed Radix - multiple bases used)

Factoradic Number System Factoradic Expansion ( 4 x 3!) + (C ( 3 x 2!) + (B ( 2 x 1!) + (A ( 1 x 0!) … (E 5 x 4!) + (D Simplify Factorials (E 5 x 24) + (D ( 4 x 6) + (C ( 3 x 2) + (B ( 2 x 1) + (A ( 1 x 1) 0 1 2 3 4 0 1 2 3 0 1 2 0 1 0 Since A, B, C, D, and E have different bases, they have different ranges of valid values

Factoradic Number System Write 2010 in Factoradic notation (E 5 x 24) + (D ( 4 x 6) + (C ( 3 x 2) + (B ( 2 x 1) + (A ( 1 x 1) 0 1 2 3 4 0 1 2 3 0 1 2 0 1 0 (3 x 3!) + (1 ( x 2!) + (0 ( x 1!) + (0 ( x 0!) = (3 x 6) + (1 ( x 2) + (0 ( x 1) = 20 Final Factoradic for 2010: 3 1 0 0

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 1

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 1 3)This 1 is the “new value” (N) If any red value to the right of N is >= N, it gets incremented by 1

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 1 3)This 1 is the “new value” (N) 12 If any red value to the right of N is >= N, it gets incremented by 1

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 1 3)This 1 is the “new value” (N) 12 If any red value to the right of N is >= N, it gets incremented by 1 4) Repeat step 3 until all red numbers have been used

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 1 3)This 1 is the “new value” (N) 12 If any red value to the right of N is 21 3 >= N, it gets incremented by 1 4) Repeat step 3 until all red numbers have been used

Obtain Permutation from Factoradic Initial Factoradic: 3 1 0 0 1) Increment every digit by 1 4 2 1 1 2) Replace right-most digit with a 1 4 2 1 3)This 1 is the “new value” (N) 1 If any red value to the right of N is 21 >= N, it gets incremented by 1 4 21 4) Repeat step 3 until all red numbers have been used 4) Decrement all numbers by 1 3 1 0 2 1 2 3 3

Use Permutation to swap bits Obtained Permutation: 3 1 0 2 Original Binary Data: 1 0 Encrypted Bit Array Data: 0 1 2 3

Use Permutation to swap bits Obtained Permutation: 3 1 0 2 Original Binary Data: 1 0 Encrypted Bit Array Data: 1 0 1 2 3

Use Permutation to swap bits Obtained Permutation: 3 1 0 2 Original Binary Data: 1 0 Encrypted Bit Array Data: 0 0 1 1 2 3

Use Permutation to swap bits Obtained Permutation: 3 1 0 2 Original Binary Data: 1 0 Encrypted Bit Array Data: 1 0 0 1 1 2 3

Use Permutation to swap bits Obtained Permutation: 3 1 0 2 Original Binary Data: 1 0 Encrypted Bit Array Data: 1 0 0 1 2 3

Project Summary Use the principles of factoradics to: • Encrypt/Decrypt any binary file on the Windows platform • Generate keys to decrypt files Like a really long password stored in a text file