DATA DAN VARIABEL 1 Berbagai aspek perencanaan dan

DATA DAN VARIABEL 1

Berbagai aspek perencanaan dan peramalan formal diilustrasikan dengan menggunakan keputusan strategis oleh Ford dalam mengenalkan mobil Edsel pada tahun 1957. Dalam situasi ini, perencanaan dan peramalan formal akan diharapkan bermanfaat. Berdasarkan laporan yang diterbitkan oleh Ford (Baker, 1957) dan seorang pengamat (Brooks, 1969), Ford tidak menggunakan perencanaan dan peramalan formal untuk keputusan strategis dalam pengenalan mobil Edsel. (Tentu saja, setelah memutuskan secara intuitif untuk melanjutkan, mereka melakukan perencanaan operasional untuk produksi mobil. ) Pengenalan Edsel dianggap sebagai salah satu kesalahan bisnis yang terbesar sepanjang masa dan Ford menderita kerugian $ 350 juta. Dealer mereka juga menderita kerugan dalam jumlah yang besar. Mungkinkah perencanaan dan peramalan formal dapat melindungi Ford dari kesalahan strategis yang besar tersebut? 2

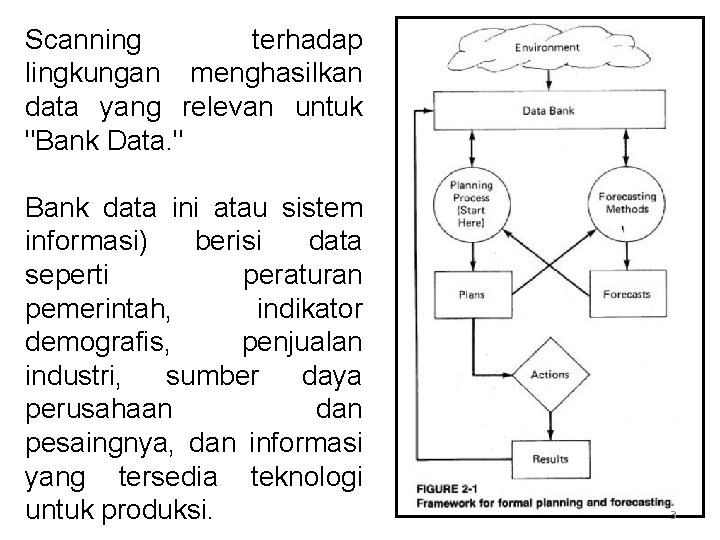
Scanning terhadap lingkungan menghasilkan data yang relevan untuk "Bank Data. " Bank data ini atau sistem informasi) berisi data seperti peraturan pemerintah, indikator demografis, penjualan industri, sumber daya perusahaan dan pesaingnya, dan informasi yang tersedia teknologi untuk produksi. 3

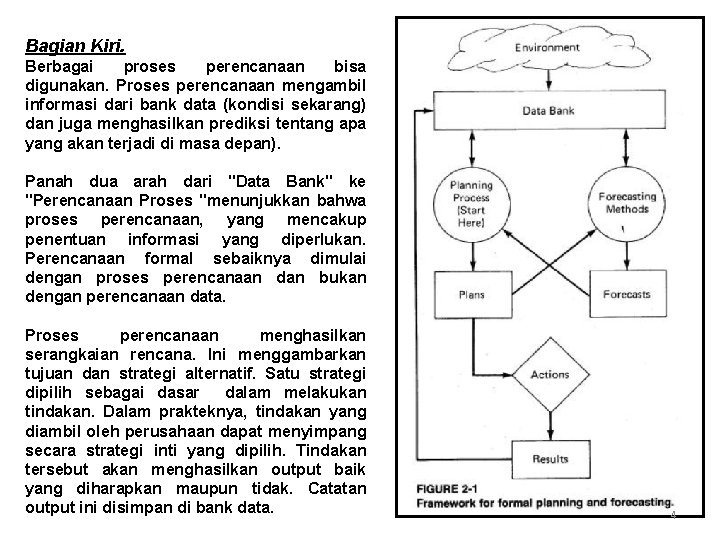
Bagian Kiri. Berbagai proses perencanaan bisa digunakan. Proses perencanaan mengambil informasi dari bank data (kondisi sekarang) dan juga menghasilkan prediksi tentang apa yang akan terjadi di masa depan). Panah dua arah dari "Data Bank" ke "Perencanaan Proses "menunjukkan bahwa proses perencanaan, yang mencakup penentuan informasi yang diperlukan. Perencanaan formal sebaiknya dimulai dengan proses perencanaan dan bukan dengan perencanaan data. Proses perencanaan menghasilkan serangkaian rencana. Ini menggambarkan tujuan dan strategi alternatif. Satu strategi dipilih sebagai dasar dalam melakukan tindakan. Dalam prakteknya, tindakan yang diambil oleh perusahaan dapat menyimpang secara strategi inti yang dipilih. Tindakan tersebut akan menghasilkan output baik yang diharapkan maupun tidak. Catatan output ini disimpan di bank data. 4

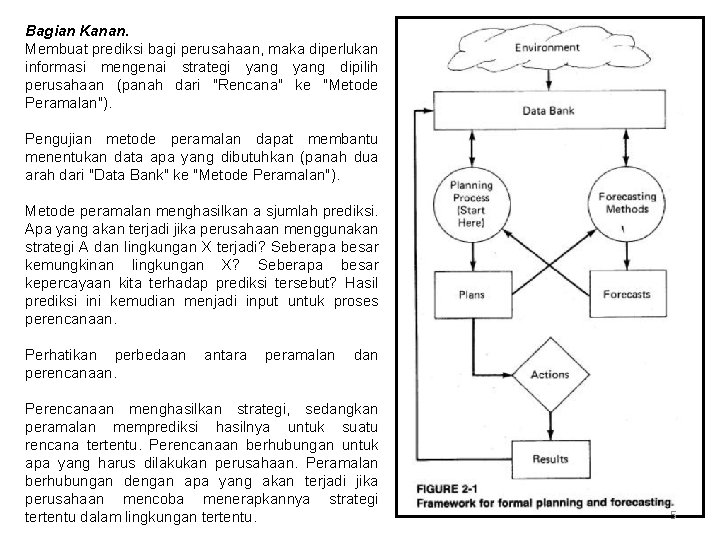
Bagian Kanan. Membuat prediksi bagi perusahaan, maka diperlukan informasi mengenai strategi yang dipilih perusahaan (panah dari "Rencana" ke "Metode Peramalan"). Pengujian metode peramalan dapat membantu menentukan data apa yang dibutuhkan (panah dua arah dari "Data Bank" ke "Metode Peramalan"). Metode peramalan menghasilkan a sjumlah prediksi. Apa yang akan terjadi jika perusahaan menggunakan strategi A dan lingkungan X terjadi? Seberapa besar kemungkinan lingkungan X? Seberapa besar kepercayaan kita terhadap prediksi tersebut? Hasil prediksi ini kemudian menjadi input untuk proses perencanaan. Perhatikan perbedaan perencanaan. antara peramalan dan Perencanaan menghasilkan strategi, sedangkan peramalan memprediksi hasilnya untuk suatu rencana tertentu. Perencanaan berhubungan untuk apa yang harus dilakukan perusahaan. Peramalan berhubungan dengan apa yang akan terjadi jika perusahaan mencoba menerapkannya strategi tertentu dalam lingkungan tertentu. 5

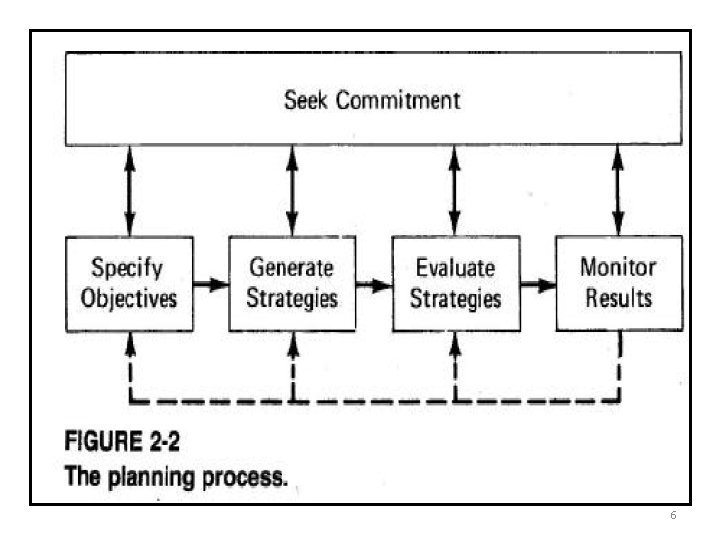
6

Definisi Variabel. a) Hatch & Farhady (1981), variabel adalah atribut seseorang atau objek yang mempunyai variasi antara satu orang dengan yang lain atau satu objek dengan objek yang lain. b) Karlinger (1973), variabel adalah konstruk atau sifat yang akan dipelajari. c) Sugiyono(2009), variabel penelitian adalah segala sesuatu yang berbentuk apa saja yang ditetapkan oleh peneliti untuk dipelajari, sehingga diperoleh informasi tentang hal tersebut, kemudian ditarik kesimpulannya. Contoh variabel penelitian: q Struktur organisasi q Kepemimpinan q Pengawasan q Koordinasi q q Prosedur dan mekanisme kerja Deskripsi pekerjaan Kebijakan Budaya organisasi. Unit analisis : Sesuatu yg dapat berupa orang, benda, atau subyek lainnya yg akan dijadikan satuan pengukuran data atau agregasi data dalam penelitian. Unit analisis dapat di tingkat individu atau kelompok 7

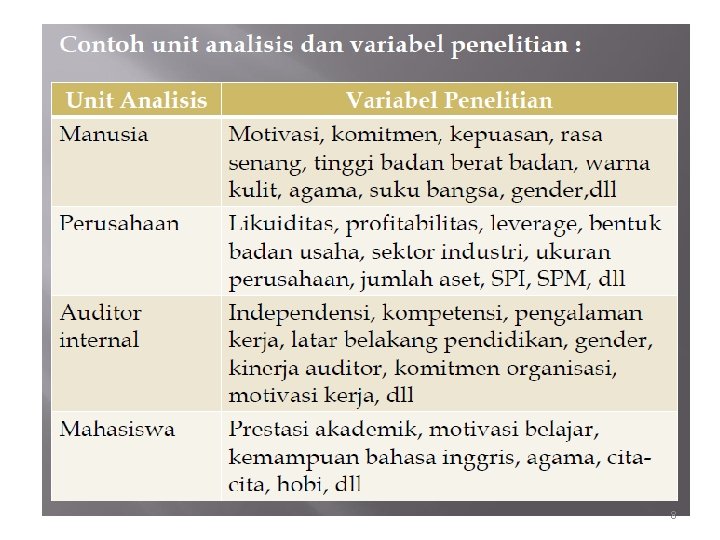
8

Berdasarkan bulat atau tidaknya nilai, variabel diklasifikasikan: q Variabel kontinu: besarannya dapat menempati nilai di semua titik q Variabel diskrit: tidak dapat menempati semua nilai, selalu bilangan bulat Jenis Data 1. Data primer dan data sekunder 2. Data kualitatif dan kuantitatif 3. Data internal dan eksternal 4. Data time series dan cross section Skala Pengukuran 1. Skala Nominal 2. Skala ordinal 3. Skala interval 4. Skala nisbah/rasio 9

MACAM-MACAM VARIABEL a) Variabel Independen (variabel stimulus/ prediktor/antecendent/ eksogen/bebas) adalah variabel yang mempengaruhi atau yang menjadi sebab perubahan atau timbulnya variabel dependen (terikat) (Sugiyono, 2009: 39). b) Variabel dependen (variabel output/kriteria/ konsekuen/endogen/ terikat) adalah variabel yang dipengaruhi atau yang menjadi akibat karena adanya variabel bebas. c) Variabel moderator (variabel independen kedua), adalah variabel yang mempengaruhi (memperkuat/ memperlemah) hubungan antara variabel independen dengan variabel dependen. d) Variabel intervening (variabel penyela/antara), adalah variabel yang secara teoritis mempengaruhi hubungan antara variabel independen dengan variabel dependen menjadi hubungan tidak langsung dan tidak dapat diamati atau diukur. Trucman (1988) dalam Sugiyono (2009: 41). e) Variabel kontrol adalah variabel yang dikendalikan atau dibuat konstan sehingga pengaruh variabel independen terhadap dependen tidak dipengaruhi oleh faktor luar yang tidak diteliti. f) Variabel luar (epsilon (e)) adalah variabel yang secara teoritis mempengaruhi variabel dependen/endogen akan tetapi tidak diteliti 10

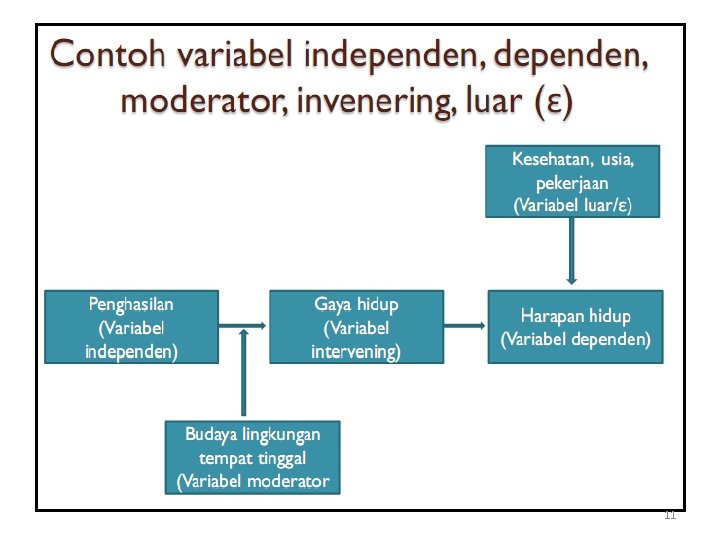
11

Pemilihan skala pengukuran akan menentukan metode analisis apakah menggunakan statistik parametrik atau statistik non parametrik. q Statistik non parametrik digunakan dalam analisis kuantitatif dimana skala ukuran variabel adalah nominal atau ordinal parametrik. q Statistik parametrik digunakan untuk skala interval atau rasio Walaupun demikian untuk skala interval atau rasio dapat juga menggunakan alat statistik non parametrik, namun banyak sekali kehilangan informasi yang dimiliki oleh data dengan skala interval dan rasio tersebut. Penggunaan statistik parametrik dan non parametrik untuk menganalisis data khususnya menguji hipotesis yang diajukan. q Contoh statistik parametrik antara lain korelasi product moment, korelasi parsial, korelasi ganda, regresi, analisis varian dan sebagainya. q Contoh statistik non parametrik adalah Chi kuadrat, Mann Whitney, Mc Memar, Cochran, Coefisien contingency, korelasi Rank Spearman, 12 Kruskal Wallis, dan sebagainya.

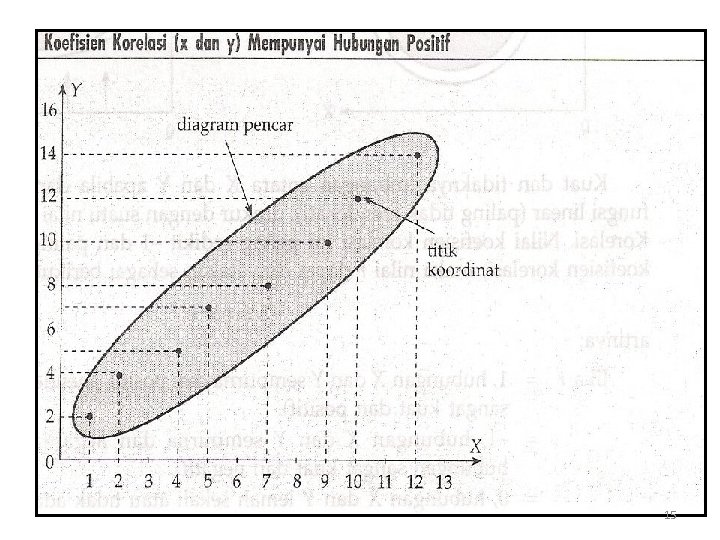
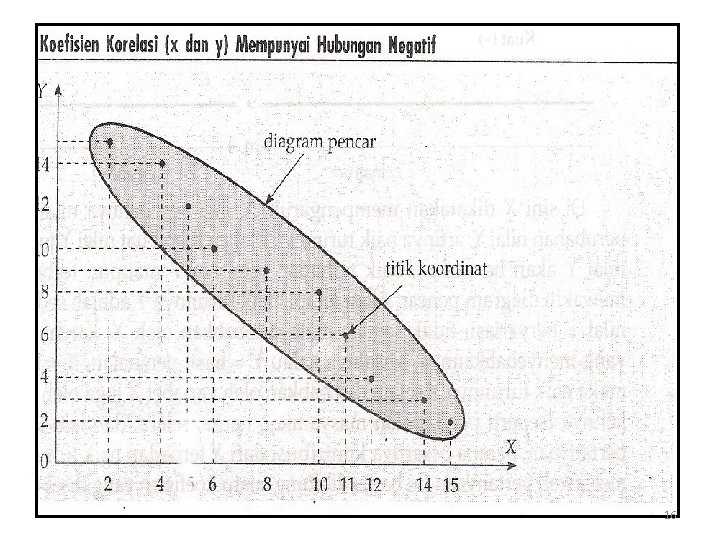
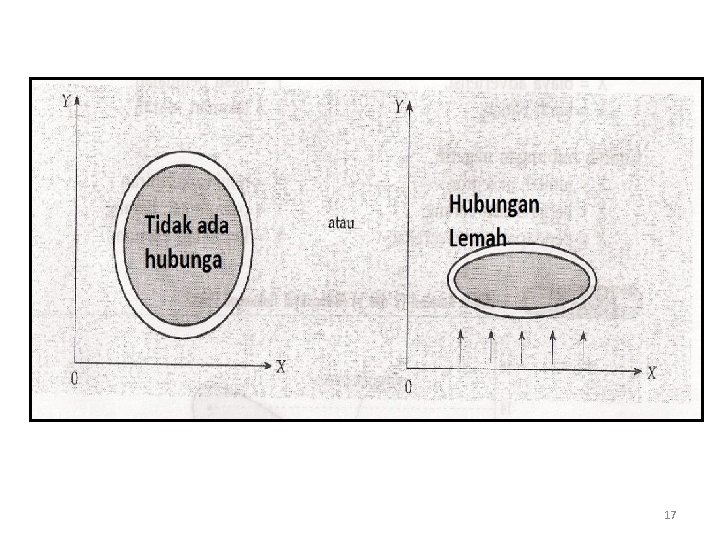
Analisis Korelasi. Secara sederhana, korelasi dapat diartikan sebagai hubungan. Korelasi merupakan salah satu teknik analisis dalam statistik yang digunakan untuk mencari hubungan antara dua variabel yang bersifat kuantitatif. Korelasi sebagai sebuah analisis memiliki berbagai jenis menurut tingkatannya. Beberapa tingkatan korelasi yang telah dikenal selama ini antara lain adalah korelasi sederhana, korelasi parsial, dan korelasi ganda. 1. Korelasi Sederhana merupakan suatu teknik statistik yang dipergunakan untuk mengukur kekuatan hubungan antara 2 variabel dan juga untuk dapat mengetahui bentuk (arah) hubungan keduanya dengan hasil yang bersifat kuantitatif. q Kekuatan hubungan antara 2 variabel yang dimaksud adalah apakah hubungan tersebut erat, lemah, ataupun tidak erat. q Bentuk (arah) hubungannya adalah apakah bentuk korelasinya linear positif ataupun linear negatif. 13

14

15

16

17

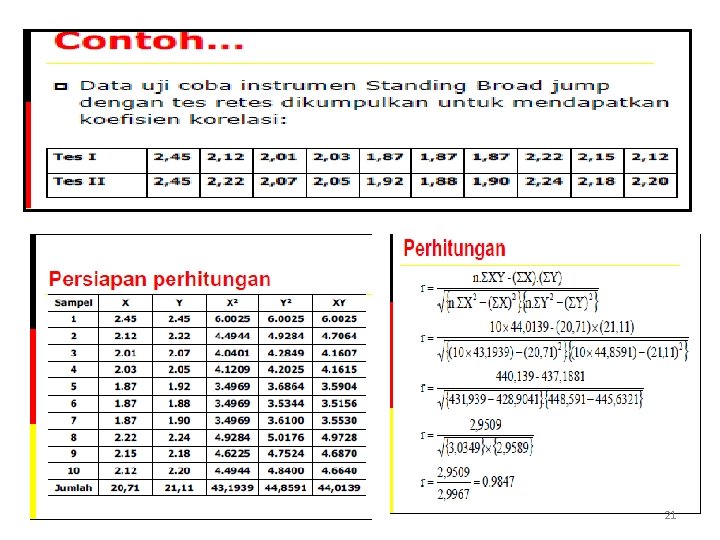
Tiga teknik korelasi: Korelasi Pearson Product Moment, Korelasi Rank Spearman, dan Koefisien Kontingensi q Korelasi Pearson Product Moment adalah korelasi untuk data kontinu dan data diskrit serta digunakan untuk statistik parametrik. Ketika data berjumlah besar dan memiliki ukuran parameter seperti mean dan standar deviasi populasi. Korelasi Pearson menghitung korelasi dengan menggunakan variasi data. Keragaman data tersebut dapat menunjukkan korelasinya. Data numerik seperti nilai tukar rupiah, data rasio keuangan, tingkat pertumbuhan ekonomi, data berat badan contoh data numerik lainnya, maka Korelasi Pearson Product Moment cocok digunakan. 18

Koefisien korelasi Pearson antara dua variabel yang datanya tidak berkelompok : 19

Untuk menentukan keeratan hubungan bisa digunakan kriteria Guilford (1956). Jika: 20

21

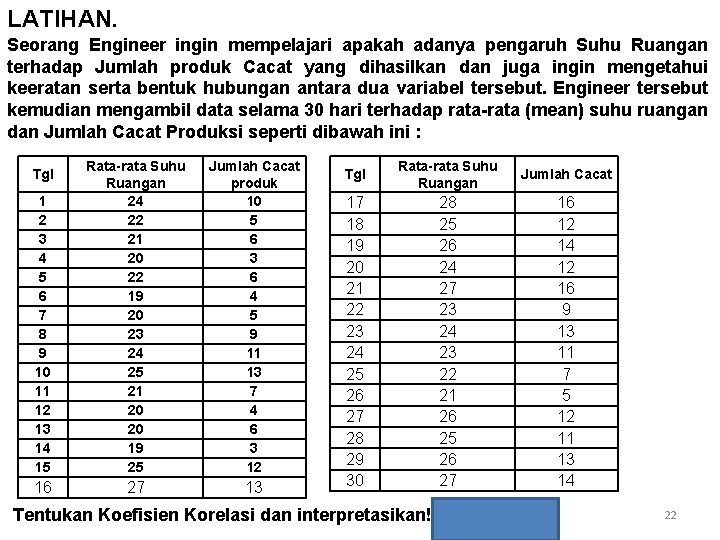
LATIHAN. Seorang Engineer ingin mempelajari apakah adanya pengaruh Suhu Ruangan terhadap Jumlah produk Cacat yang dihasilkan dan juga ingin mengetahui keeratan serta bentuk hubungan antara dua variabel tersebut. Engineer tersebut kemudian mengambil data selama 30 hari terhadap rata-rata (mean) suhu ruangan dan Jumlah Cacat Produksi seperti dibawah ini : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Rata-rata Suhu Ruangan 24 22 21 20 22 19 20 23 24 25 21 20 20 19 25 Jumlah Cacat produk 10 5 6 3 6 4 5 9 11 13 7 4 6 3 12 16 27 13 Tgl Rata-rata Suhu Ruangan Jumlah Cacat 17 18 19 20 21 22 23 24 25 26 27 28 29 30 28 25 26 24 27 23 24 23 22 21 26 25 26 27 16 12 14 12 16 9 13 11 7 5 12 11 13 14 Tentukan Koefisien Korelasi dan interpretasikan! r = 0. 955458 22

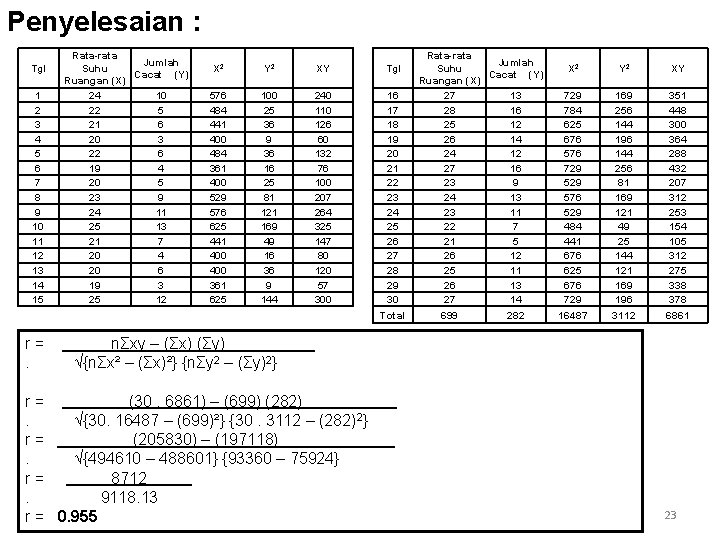
Penyelesaian : Tgl 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 r=. Rata-rata Jumlah Suhu Cacat (Y) Ruangan (X) 24 10 22 5 21 6 20 3 22 6 19 4 20 5 23 9 24 11 25 13 21 7 20 4 20 6 19 3 25 12 X 2 Y 2 XY Tgl 576 484 441 400 484 361 400 529 576 625 441 400 361 625 100 25 36 9 36 16 25 81 121 169 49 16 36 9 144 240 110 126 60 132 76 100 207 264 325 147 80 120 57 300 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Total Rata-rata Jumlah Suhu Cacat (Y) Ruangan (X) 27 13 28 16 25 12 26 14 24 12 27 16 23 9 24 13 23 11 22 7 21 5 26 12 25 11 26 13 27 14 699 282 X 2 Y 2 XY 729 784 625 676 576 729 576 529 484 441 676 625 676 729 16487 169 256 144 196 144 256 81 169 121 49 25 144 121 169 196 3112 351 448 300 364 288 432 207 312 253 154 105 312 275 338 378 6861 nΣxy – (Σx) (Σy) √{nΣx² – (Σx)²} {nΣy 2 – (Σy)2} r= (30. 6861) – (699) (282). √{30. 16487 – (699)²} {30. 3112 – (282)2} r= (205830) – (197118). √{494610 – 488601} {93360 – 75924} r= 8712. 9118. 13 r = 0. 955 23

q Korelasi Rank Spearman digunakan untuk data diskrit dan kontinu serta untuk statistik nonparametrik. Statistik nonparametrik adalah statistik yang digunakan ketika data tidak memiliki informasi parameter, data tidak berdistribusi normal atau data diukur dalam bentuk ranking. Korelasi Pearson ini tidak memerlukan asumsi normalitas dan cocok juga digunakan untuk data dengan sampel kecil. Korelasi Rank Spearman menghitung korelasi dengan menghitung ranking data terlebih dahulu berdasarkan orde data. ü ü Ketika peneliti berhadapan dengan data kategorik seperti kategori pekerjaan, tingkat pendidikan, kelompok usia, maka Korelasi Rank Spearman cocok digunakan. Korelasi Rank Spearman pun cocok digunakan pada kondisi dimana peneliti dihadapkan pada data numerik (kurs rupiah, rasio keuangan, pertumbuhan ekonomi), namun peneliti tidak memiliki cukup banyak 24 data (data kurang dari 30).

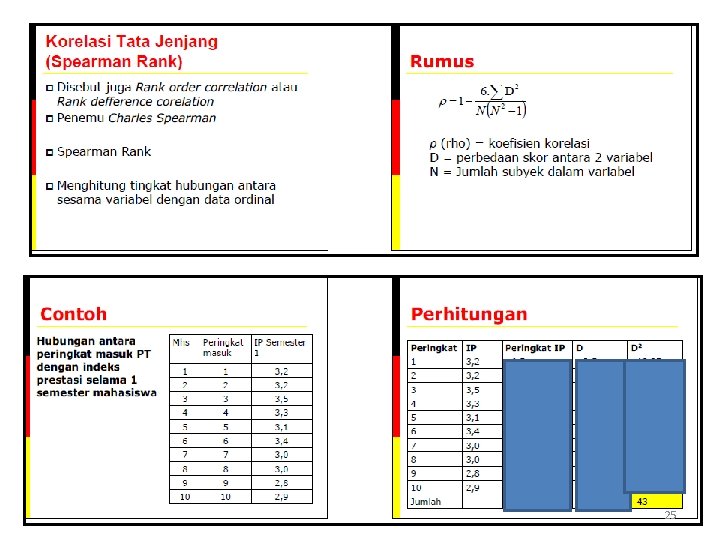
25

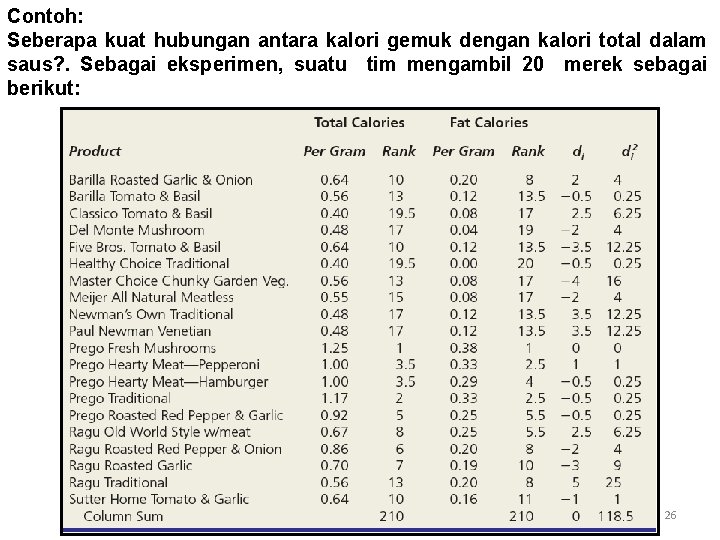
Contoh: Seberapa kuat hubungan antara kalori gemuk dengan kalori total dalam saus? . Sebagai eksperimen, suatu tim mengambil 20 merek sebagai berikut: 26

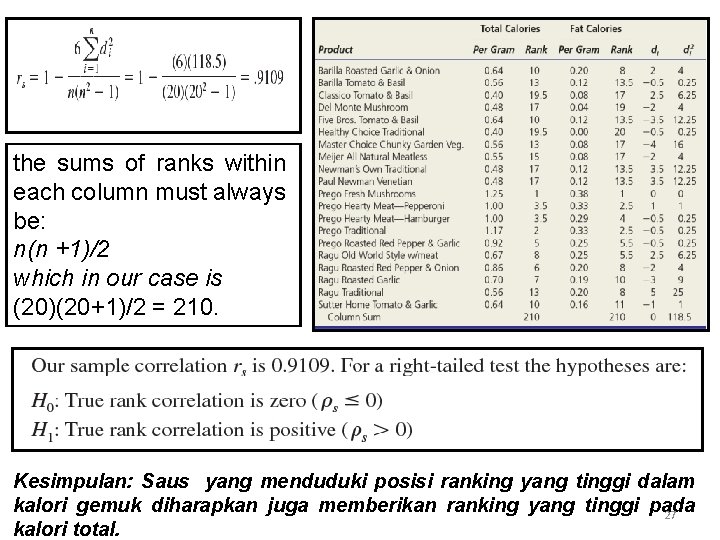
the sums of ranks within each column must always be: n(n +1)/2 which in our case is (20)(20+1)/2 = 210. Kesimpulan: Saus yang menduduki posisi ranking yang tinggi dalam kalori gemuk diharapkan juga memberikan ranking yang tinggi pada 27 kalori total.

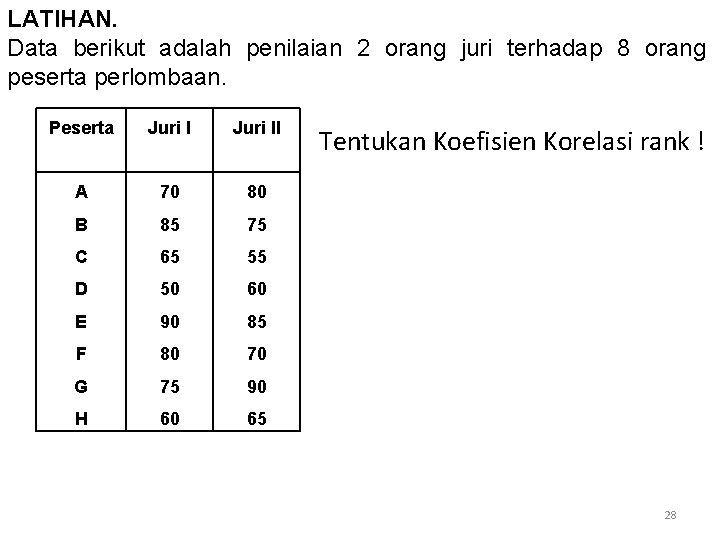
LATIHAN. Data berikut adalah penilaian 2 orang juri terhadap 8 orang peserta perlombaan. Peserta Juri II A 70 80 B 85 75 C 65 55 D 50 60 E 90 85 F 80 70 G 75 90 H 60 65 Tentukan Koefisien Korelasi rank ! 28

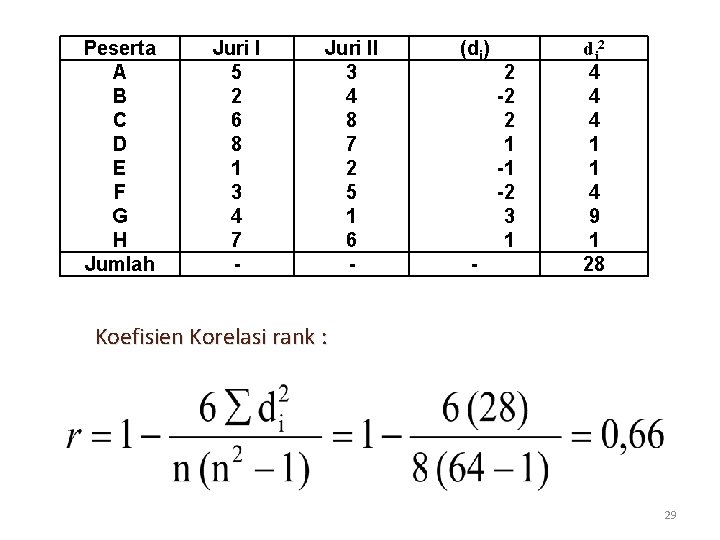
Peserta A B C D E F G H Jumlah Juri I 5 2 6 8 1 3 4 7 - Juri II 3 4 8 7 2 5 1 6 - (di) - 2 -2 2 1 -1 -2 3 1 di 2 4 4 4 1 1 4 9 1 28 Koefisien Korelasi rank : 29

q Koefisien Kontingensi dan Korelasi Poin Biserial 30

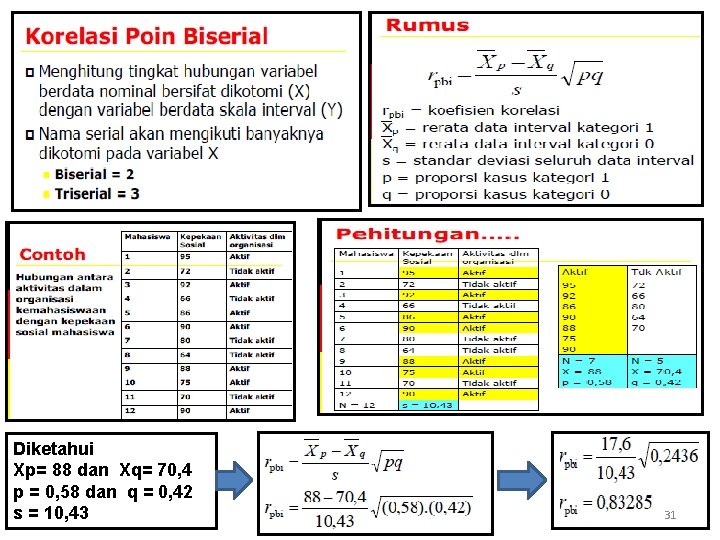
Diketahui Xp= 88 dan Xq= 70, 4 p = 0, 58 dan q = 0, 42 s = 10, 43 31