Data dan Penyajian Data Penyajian Data penelitian harus

Data dan Penyajian Data

Penyajian Data penelitian harus disusun dan disajikan dalam bentuk yang mudah dipahami. Penyusunan dan penyajian data penting untuk memudahkan : Analisis dan pembacaan data hasil penelitian. Penyajian data dapat dengan tabel frekuensi atau diagram (grafik)

Kelompok Data Kualitatif Kuantitatif Skala nominal Skala interval Skala ordinal Skala rasio

Skala pengukuran 1. Skala nominal adalah skala yang mempunyai ciri untuk membedakan skala ukur yang satu dengan yang lain. Untuk menggunakan skala nominal ini, data diklasifikasikan dalam kelompok/kategori. Tiap kategori mungkin diberi lambing, symbol, atau angka yang berfungsi untuk membedakan saja. Contoh penggunaan skala nominal dapat dilihat pada tabel disamping Negara Jml perusahaan yg memperoleh sertifikat ISO Indonesia 55 Brunei 5 RRC 285 Hong Kong 551 Jepang 1827 Malaysia 628 Filipina 79

2. Skala ordinal adalah skala yang mempunyai ciri membedakan dan mengurutkan, misalnya dari yang paling rendah sampai paling tinggi, paling sedikit sampai paling banyak. Contoh penggunaan skala ordinal dapat dilihat pada tebel di samping. Kelompok nilai Jumlah siswa Sangat tinggi 7 Tinggi 14 Sedang 11 Rendah 2 Sangat rendah 3

3. Skala interval bukan hanya berfungsi sebagai nominal (membedakan) dan ordinal (mengurutkan), namun juga menunjukkan ciri jarak yang sama. Contoh misalnya penggunaan derajat celcius untuk menentukan tingginya suhu di suatu tempat, misalnya 29 derajat celcius, 30 derajat celcius, dan seterusnya. Angka nol pada skala ini tidak berarti “kosong” atau tidak ada. Misalnya, suhu nol derajat celcius tidak berari tidak ada panas. 4. Skala rasio mempunyai ciri membedakan, mengurutkan, jarak yang sama, dan mempunyai titik nol yang berarti. Misalnya : Jumlah mahasiswa yang hadir nol (artinya tidak ada mahasiswa yang hadir). Jumlah mahasiswa yang hadir hari selasa 40, sedangkan yang hadir pada hari senin 20. (jadi yang hadir pada hari selasa dua kali lipat yang hadir hari senin)

Penyajian data Penyajian Data Dalam bentuk Tabel frekuensi Kategori Frekuensi Persentase

Penyajian Data Penyajian data dalam bentuk diagram (grafik) ◦ Berisi seluruh informasi data disajikan sehingga pembaca tdk perlu mencari informasi utk memahami grafik di dalam teks. ◦ Nomor diagram, judul, serta jumlah data, data interval rasio angka dari setiap kategori harus jelas terlihat. Grafik Jumlah Siswa Bimbel Jakarta

Penyajian Data Kelebihan dan kekurangan melakukan penyajian dengan grafik Kelebihan Kekurangan -lebih mudah diingat -lebih menarik -informasi visual dan dapat diperbandingkan -menyajikan perubahan hubungan -penyajiannya harus sesuai tujuan -gambaran umum -dipengaruhi skala

PENYAJIAN DATA KUALITATIF

Data Kualitatif Data kualitatif umumnya dihasilkan dari pertanyaan terbuka (pertanyaan yang kategori jawabannya tidak dibatasi oleh si peneliti). ◦ Contoh pertanyaan terbuka : “ Mengapa anda mencari pekerjaan di Korea? ” ◦ Jawabannya akan beraneka ragam, perlu pengelompokan (penyederhanaan) jawaban

Data kualitatif Di korea lebih mudah mencari pekerjaan Korea menjanjikan gaji yang besar Korea lebih banyak peluang Pekerjaan apapun menghasilkan uang Di Indonesia sulit mencari pekerjaan Di Indonesia banyak perusahaan gulung tikar Di Indonesia membutuhkan keahlian tertentu untuk dapat pekerjaan

Penyajian & Interpretasi data Penyajian data dalam bentuk tabel frekuensi (tabel distribusi frekuensi kualitatif) ◦ Adanya pembagian kelas yang didasarkan atas kategori-kategori tertentu ◦ Contoh : interpretasi apa yang dapat diperoleh dari tabel dibawah ini ?

Penyajian & Interpretasi data Penyajian data dalam bentuk diagram lingkaran (pie chart) dan diagram batang (bar chart) Kategori dalam pie chart : (n/N) x 360 o atau (n/N) x 100% Kategori dalam diagram batang diwakilkan oleh suatu persegi panjang

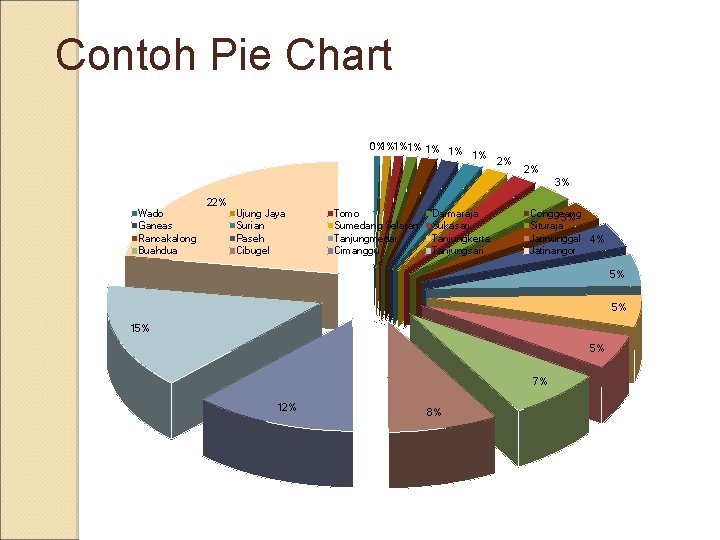
Contoh Pie Chart 0%1%1%1% 1% 2% 2% 3% Wado Ganeas Rancakalong Buahdua 22% Ujung Jaya Surian Paseh Cibugel Tomo Sumedang Selatan Tanjungmedar Cimanggu Darmaraja Sukasari Tanjungkerta Tanjungsari Conggeang 3% Situraja Jatinunggal 4% Jatinangor 5% 5% 15% 5% 7% 12% 8%

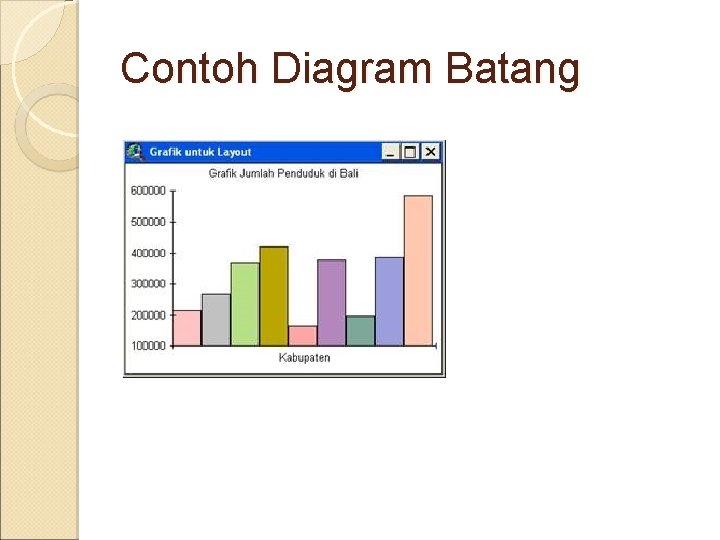
Contoh Diagram Batang

PENYAJIAN DATA KUANTITATIF

Data Kuantitatif Data kuantitatif berdasarkan pengukuran interval dan rasio ◦ Data dari responden umumnya bervariasi sehingga memerlukan penyederhanaan data dengan cara mengelompokkan data menjadi kelas-kelas dan interval tertentu ◦ Kaidah yang dipakai untuk penyederhanaan data biasanya menggunakan kaidah sturgess

Jenis Data Berdasar nilainya, ada dua jenis data kuantitatif : diskrit : diperoleh dari hasil perhitungan kontinyu : diperoleh dari hasil pengukuran, sehingga umumnya dibutuhkan alat ukur tertentu untuk mendapatkan datanya

Penyederhanaan data (Distribusi Frekuensi) Distribusi frekuensi ◦ Pengelompokan data ke dalam beberapa kategori yang menunjukan banyaknya data dalam setiap kategori dan setiap data tidak dapat dimasukan ke dalam dua atau lebih kategori Tujuan ◦ Data menjadi informatif dan mudah dipahami

Langkah – langkah Penyederhanaan data (Distribusi Frekuensi) Mengurutkan data Membuat ketegori atau kelas data Membuat Interval data Membuat Tabel Frekuensi Melakukan penturusan atau tabulasi, memasukan nilai ke dalam interval kelas

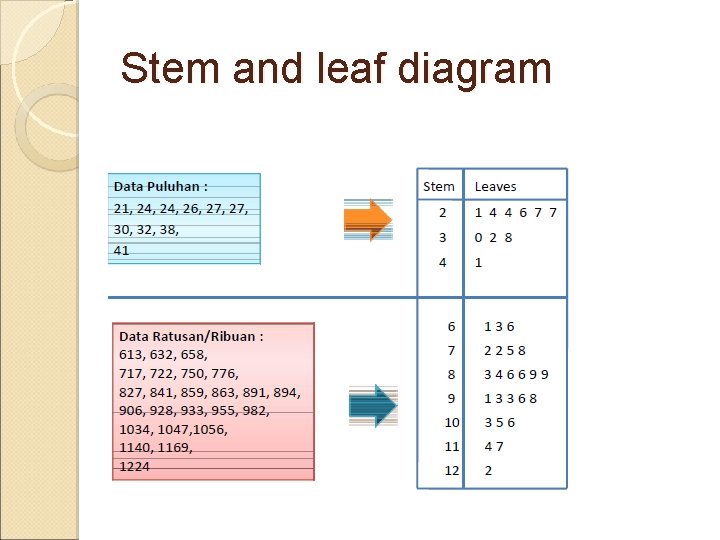
Penyajian data dan interpretasinya Tabel frekuensi Diagram (grafik) terdiri dari : ◦ Histogram : sama dengan diagram batang, hanya batangnya menempel (tidak terpisah) karena data yang disajikan bersifat Kontinyu ◦ Poligon Frekuensi : grafik yang dihasilkan dengan menghubungkan puncak dari masing-masing nilai tengah kelas histogram. ◦ Ogive : diagram yang dibuat dari frekuensi kumulatif. Sumbu horizontal menggunakan kelas, sedangkan sumbu vertikal menggunakan frekuensi kumulatif ◦ Stem and leaf diagram (grafik batang daun) : Batang = bilangan-bilangan, Daun = bilangan sisanya

Langkah Pertama Mengurutkan data : dari yang terkecil (Min) ke yang terbesar (Max) atau sebaliknya Tujuan : ◦ Untuk memudahkan dalam melakukan perhitungan pada langkah ketiga

Langkah Pertama Data diurut dari terkecil ke terbesar Nilai terkecil 215 Nilai terbesar 9750 No Nama Kecamatan ∑ Masyarakat yang dilayani 1. Wado 215 2. Ujung Jaya 290 3. Tomo 310 4. Darmaraja 365 5. Conggeang 530 6. Ganeas 580 7. Surian 650 8. Sumedang Selatan 750 9. Sukasari 840 10. Situraja 1200 11. Rancakalong 1280 12. Paseh 1580 13. Tanjungmedar 2050 14. Tanjungkerta 2075 15. Jatinunggal 2175 16. Buahdua 3150 17. Cibugel 3600 18. Cimanggu 5350 19. Tanjungsari 6600 20. Jatinangor 9750

Langkah Kedua Membuat kategori atau kelas data ◦ Tidak ada aturan pasti, berapa banyaknya kelas ! Langkah : ◦ Banyaknya kelas/kategori sesuai dengan kebutuhan

Langkah kedua Gunakan pedoman bilangan bulat terkecil k, dengan demikian sehingga 2 k n atau aturan Sturges Jumlah kategori (k) = 1 + 3, 322 Log n Contoh n = 20 (k) = 1 + 3, 322 Log 20 l a m i in m (k) = 1 + 3, 322 (1, 301) h a 5 l u m t i u J i ya r o g (k) = 1 + 4, 322 Kete (k) = 5, 322

Langkah ketiga Tentukan interval kelas : batas kelas nyata dan batas kelas semu. Interval kelas adalah batas bawah dan batas dari suatu kategori Rumus : Nilai terbesar - terkecil Interval kelas = R /K= Jumlah kelas

Interval Kelas Batas kelas nyata: antara kelas tidak terdapat loncatan nilai ◦ Range (R)= (Max+0, 5) – (Min-0, 5) ◦ K=kategori/Jumlah kelas ◦ interval=R/K= (Max+0, 5) – (Min-0, 5) /K Batas kelas semu: antara kelas terdapat loncatan nilai

Contoh Berdasarkan data ◦ Nilai tertinggi ◦ Nilai terendah Interval kelas = 9750 = 215 : ◦ = [ 9750 – 215 ] / 5 ◦ = 1907 Jadi interval kelas 1907 yaitu jarak nilai terendah dan nilai tertinggi dalam suatu kelas atau kategori

Interval kelas batas kelas semu Nilai tertinggi : = 215 + 1907 = 2122 Nilai terendah Kelas ke 2 = 2122 + 1 = 2123 Ada loncatan nilai antara kelas

Interval kelas batas kelas nyata Kelas Batas Kelas nyata 1 214, 5 x ≤ 2122, 5 2 2122, 5 x ≤ 4030, 5 3 4030, 5 x ≤ 5938, 5 4 5398, 5 x ≤ 7846, 5 5 7846, 5 x ≤ 9754, 5 Tidak ada loncatan kelas

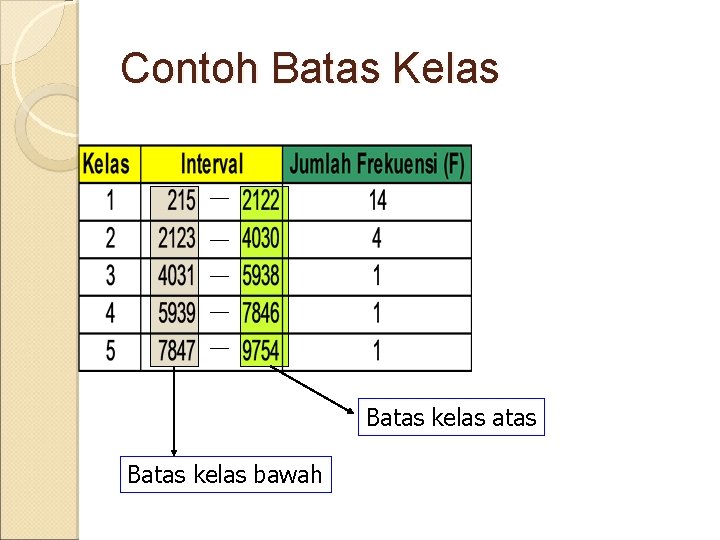
Penyajian Data Batas kelas ◦ Nilai terendah dan tertinggi Batas kelas dalam suatu interval kelas terdiri dari dua macam : ◦ Batas kelas bawah – lower class limit Nilai teredah dalam suatu interval kelas ◦ Batas kelas atas – upper class limit Nilai teringgi dalam suatu interval kelas

Contoh Batas Kelas Batas kelas atas Batas kelas bawah

Langkah keempat Lakukan penturusan atau tabulasi data Kelas Interval Frekuensi Jumlah Frekuensi (F) 1 215 2122 IIIII 14 2 2123 4030 III 3 3 4031 5938 I 1 4 5939 7846 I 1 5 7847 9754 I 1

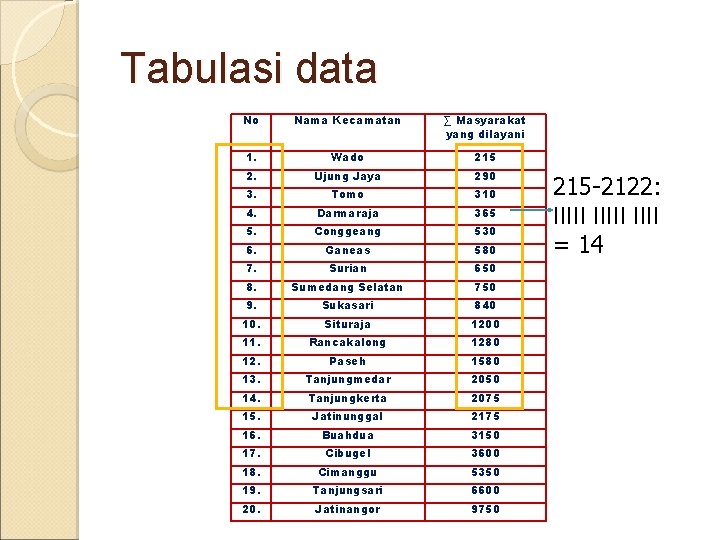
Tabulasi data No Nama Kecamatan ∑ Masyarakat yang dilayani 1. Wado 215 2. Ujung Jaya 290 3. Tomo 310 4. Darmaraja 365 5. Conggeang 530 6. Ganeas 580 7. Surian 650 8. Sumedang Selatan 750 9. Sukasari 840 10. Situraja 1200 11. Rancakalong 1280 12. Paseh 1580 13. Tanjungmedar 2050 14. Tanjungkerta 2075 15. Jatinunggal 2175 16. Buahdua 3150 17. Cibugel 3600 18. Cimanggu 5350 19. Tanjungsari 6600 20. Jatinangor 9750 215 -2122: IIIII = 14

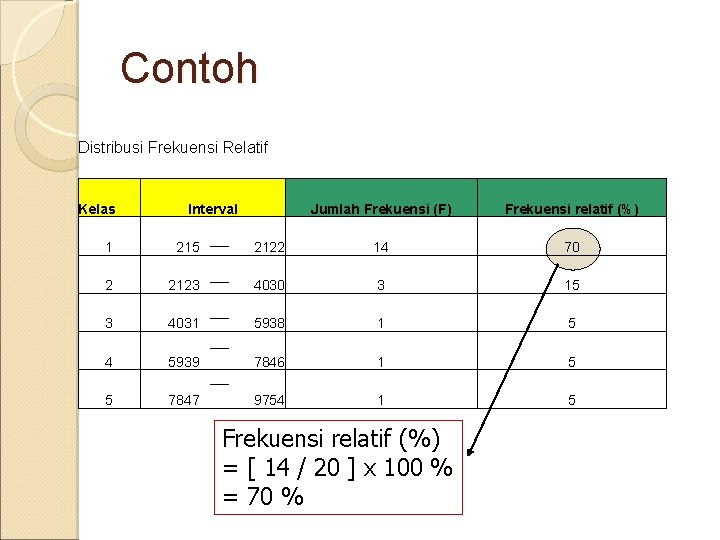
Distribusi Frekuensi Relatif Frekuensi setiap kelas dibandingkan dengan frekuensi total Tujuan ; Untuk memudahkan membaca data secara tepat dan tidak kehilangan makna dari kandungan data

Contoh Distribusi Frekuensi Relatif Kelas Interval Jumlah Frekuensi (F) Frekuensi relatif (%) 1 215 2122 14 70 2 2123 4030 3 15 3 4031 5938 1 5 4 5939 7846 1 5 5 7847 9754 1 5 Frekuensi relatif (%) = [ 14 / 20 ] x 100 % = 70 %

Nilai Tengah Tanda atau perinci dari suatu interval kelas dan merupakan suatu angka yang dapat dianggap mewakili suatu interval kelas Nilai tengah kelasnya berada di tengah-tengah pada setiap interval kelas

Contoh Nilai Tengah Nilai tengah Kelas ke 1 = [ 215 + 2122] / 2 = 1168. 5

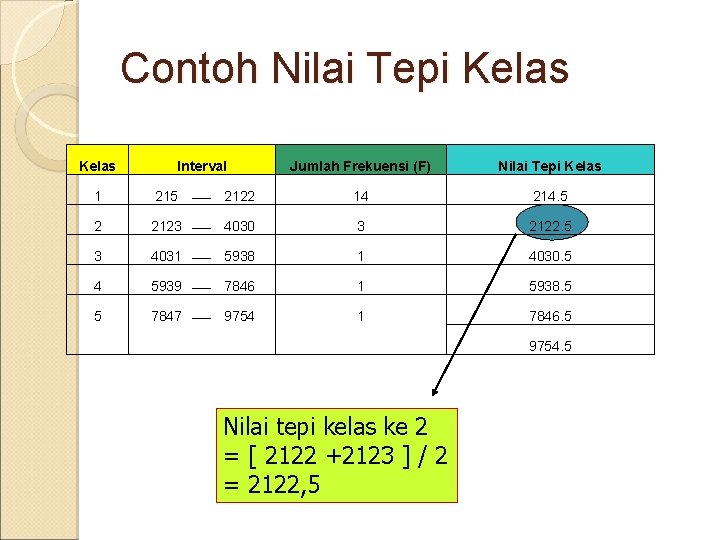
Nilai Tepi Kelas – Class Boundaries Nilai batas antara kelas yang memisahkan nilai antara kelas satu dengan kelas lainnya Penjumlahan nilai atas kelas dengan nilai bawah kelas diantaranya dan di bagi dua

Contoh Nilai Tepi Kelas Interval Jumlah Frekuensi (F) Nilai Tepi Kelas 1 215 2122 14 214. 5 2 2123 4030 3 2122. 5 3 4031 5938 1 4030. 5 4 5939 7846 1 5938. 5 5 7847 9754 1 7846. 5 Nilai tepi kelas ke 2 = [ 2122 +2123 ] / 2 = 2122, 5 9754. 5

Frekuensi Kumulatif Menunjukan seberapa besar jumlah frekuensi pada tingkat kelas tertentu Diperoleh dengan menjumlahkan frekuensi pada kelas tertentu dengan frekuensi kelas selanjutnya Frekuensi kumulatif terdiri dari ; ◦ Frekuensi kumulatif kurang dari ◦ Frekuensi kumulatif lebih dari

Frekuensi kumulatif kurang dari Merupakan penjumlahan dari mulai frekuensi terendah sanpai kelas tertinggi dan jumlah akhirnya merupakan jumlah data (n) Kelas Interval Nilai Tepi Kelas Frekuensi kumulatif Kurang dari 1 215 2122 214. 5 0 2 2123 4030 2122. 5 14 3 4031 5938 4030. 5 17 4 5939 7846 5938. 5 18 5 7847 9754 7846. 5 19 9754. 5 20 0+0=0 0 + 14 = 14

Frekuensi kumulatif lebih dari Merupakan pengurangan dari jumlah data (n) dengan frekuensi setiap kelas dimulai dari kelas terendah dan jumlah akhirnya adalah nol Kelas Interval Nilai Tepi Kelas Frekuensi kumulatif Lebih dari 1 215 2122 214. 5 20 2 2123 4030 2122. 5 6 3 4031 5938 4030. 5 3 4 5939 7846 5938. 5 2 5 7847 9754 7846. 5 1 9754. 5 0 20 – 0 = 20 20 – 14 = 6

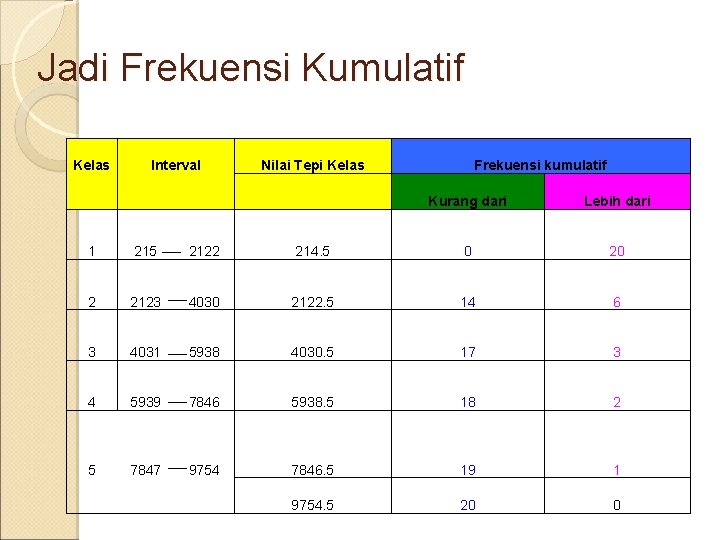
Jadi Frekuensi Kumulatif Kelas Interval Frekuensi kumulatif Kurang dari Lebih dari 1 215 2122 214. 5 0 20 2 2123 4030 2122. 5 14 6 3 4031 5938 4030. 5 17 3 4 5939 7846 5938. 5 18 2 5 7847 9754 7846. 5 19 1 9754. 5 20 0 Nilai Tepi Kelas

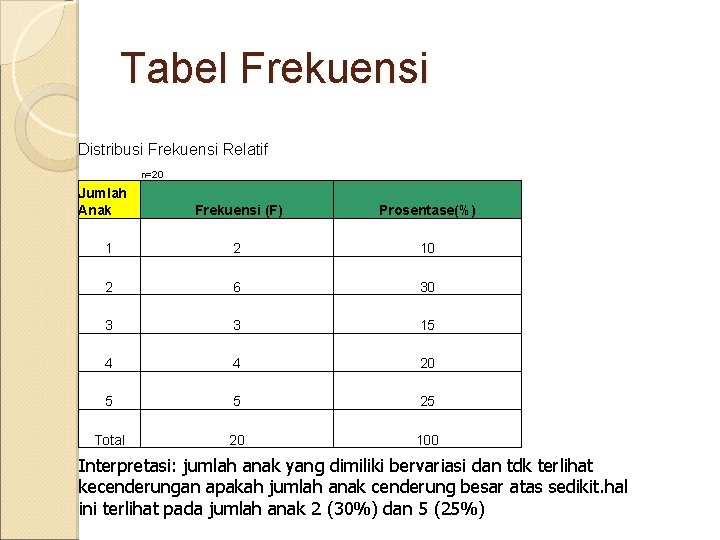
Tabel Frekuensi Distribusi Frekuensi Relatif n=20 Jumlah Anak Frekuensi (F) Prosentase(%) 1 2 10 2 6 30 3 3 15 4 4 20 5 5 25 Total 20 100 Interpretasi: jumlah anak yang dimiliki bervariasi dan tdk terlihat kecenderungan apakah jumlah anak cenderung besar atas sedikit. hal ini terlihat pada jumlah anak 2 (30%) dan 5 (25%)

Grafik dapat digunakan sebagai laporan Mengapa menggunakan grafik ? ◦ Manusia pada umunya tertarik dengan gambar dan sesuatu yang ditampilkan delam bentuk visual akan lebih mudah diingat dari pada dalam bentuk angka Grafik dapat digunakan sebagi kesimpulan tanpa kehilangan makna

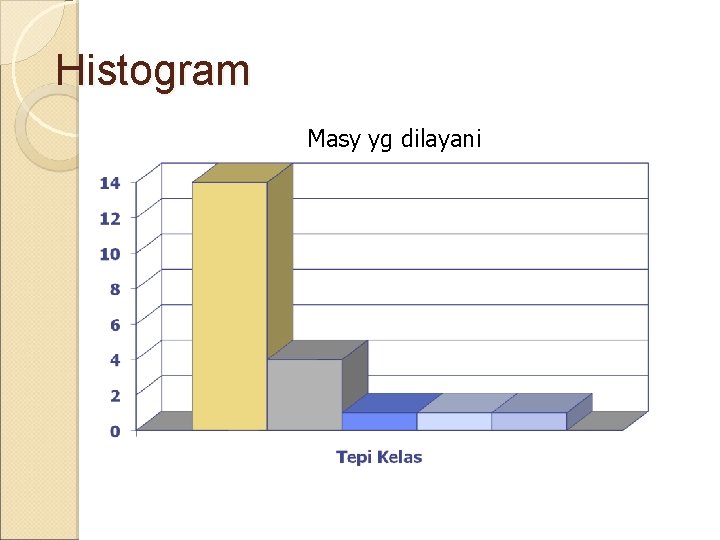
Grafik Histogram merupakan diagram balok Histogram menghubungkan antara tepi kelas interval dengan pada sumbu horizontal (X) dan frekuensi setiap kelas pada sumbu vertikal (Y) Kelas Interval Jumlah Frekuensi (F) 1 215 2122 14 2 2123 4030 3 3 4031 5938 1 4 5939 7846 1 5 7847 9754 1

Histogram Masy yg dilayani

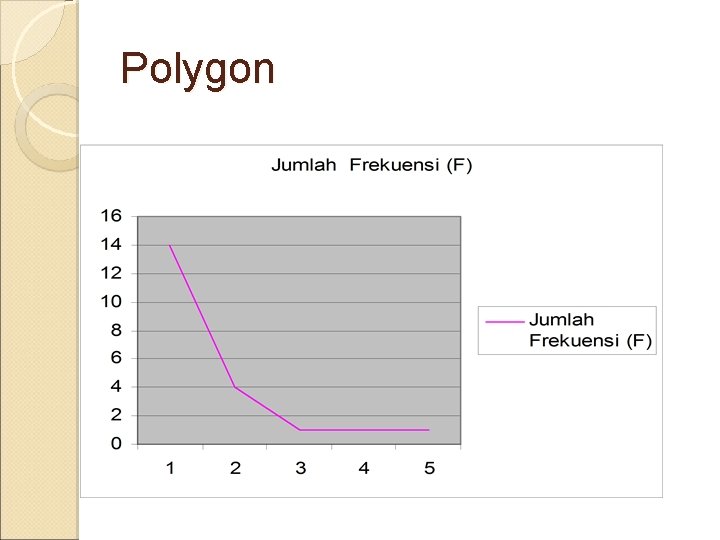
Grafik Polygon Menggunakan garis yang mengubungkan titik – titik yang merupakan koordinat antara nilai tengah kelas dengan jumlah frekuensi pada kelas tersebut Kelas 1 2 3 4 5 Nilai Tengah 1168. 5 3076. 5 4984. 5 6892. 5 8800. 5 Jumlah Frekuensi (F) 14 3 1 1 1

Polygon

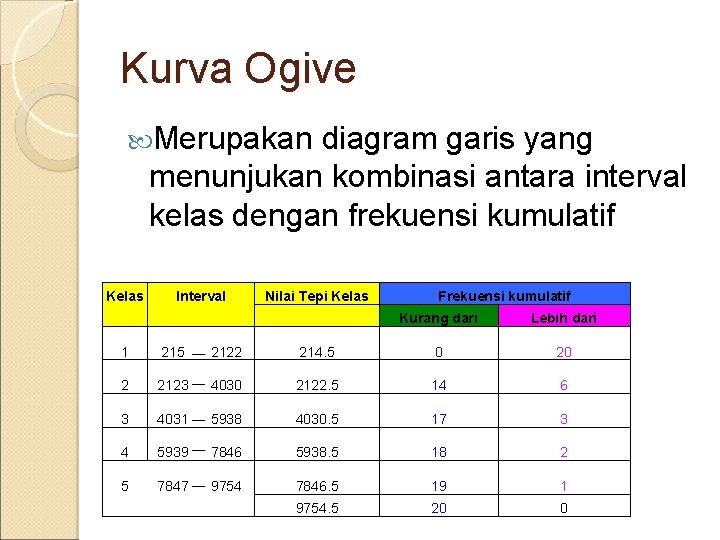
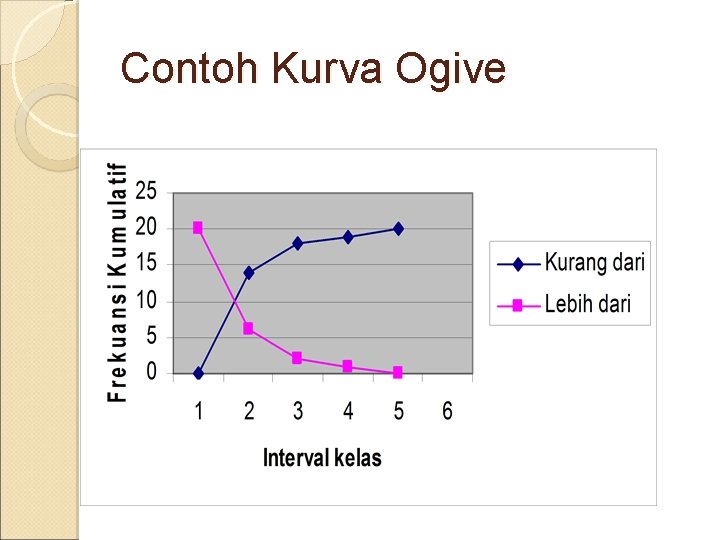
Kurva Ogive Merupakan diagram garis yang menunjukan kombinasi antara interval kelas dengan frekuensi kumulatif Kelas Interval Nilai Tepi Kelas Frekuensi kumulatif Kurang dari Lebih dari 1 215 2122 214. 5 0 20 2 2123 4030 2122. 5 14 6 3 4031 5938 4030. 5 17 3 4 5939 7846 5938. 5 18 2 5 7847 9754 7846. 5 19 1 9754. 5 20 0

Contoh Kurva Ogive

Stem and leaf diagram

Latihan LATIHAN : Berikut dilaporkan sebaran data waktu keterlambatan 50 pegawai yang tidak mengikuti apel pagi (menit Buatlah - Tabel Distribusi Frekuensi Kumulatif

Latihan : Contoh : Data berikut merupakan nilai ujian Mata Kuliah Pengantar Statistika Sosial dari 34 Praja 71 68 82 75 75 90 72 75 57 88 62 68 88 71 68 65 64 75 74 68 80 71 79 75 75 81 84 80 82 81 75 90 48 57