Data Converters EECT 7327 Oversampling ADC Fall 2014

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Oversampling ADC – 1–

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Nyquist-Rate ADC • The “black box” version of the quantization process • Digitizes the input signal up to the Nyquist frequency (fs/2) • Minimum sampling frequency (fs) for a given input bandwidth • Each sample is digitized to the maximum resolution of the converter – 2–

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Anti-Aliasing Filter (AAF) – 3– • Input signal must be bandlimited prior to sampling • Nyquist sampling places stringent requirement on the roll-off characteristic of AAF • Often some oversampling is employed to relax the AAF design (better phase response too) • Decimation filter (digital) can be linear-phase

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Oversampling ADC • Sample rate is well beyond the signal bandwidth • Coarse quantization is combined with feedback to provide an accurate estimate of the input signal on an “average” sense • Quantization error in the coarse digital output can be removed by the digital decimation filter • The resolution/accuracy of oversampling converters is achieved in a sequence of samples (“average” sense) rather than a single sample; the usual concept of DNL and INL of Nyquist converters are not applicable – 4–

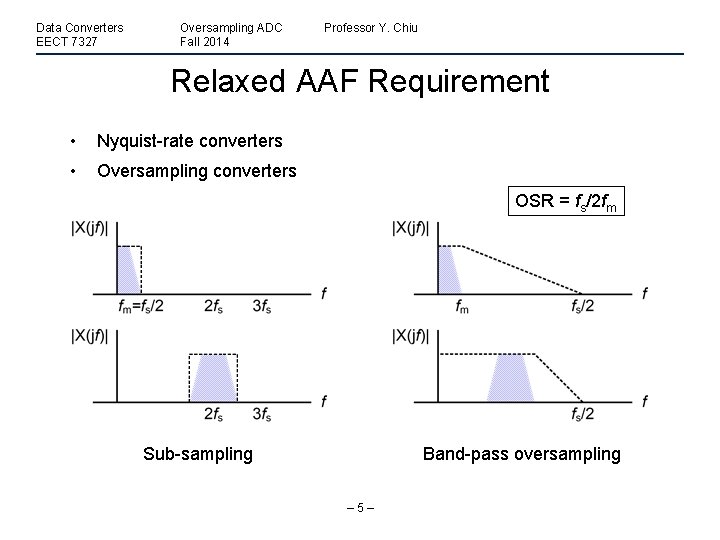
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Relaxed AAF Requirement • Nyquist-rate converters • Oversampling converters OSR = fs/2 fm Band-pass oversampling Sub-sampling – 5–

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Oversampling ADC • Predictive type – Delta modulation • Noise-shaping type – Sigma-delta modulation – Multi-level (quantization) sigma-delta modulation – Multi-stage (cascaded) sigma-delta modulation (MASH) – 6–

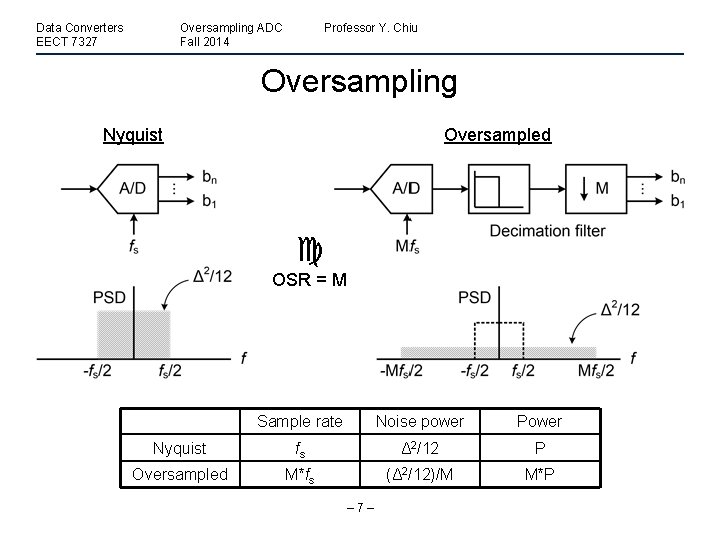
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Oversampling Nyquist Oversampled OSR = M Sample rate Noise power Power Nyquist fs Δ 2/12 P Oversampled M*fs (Δ 2/12)/M M*P – 7–

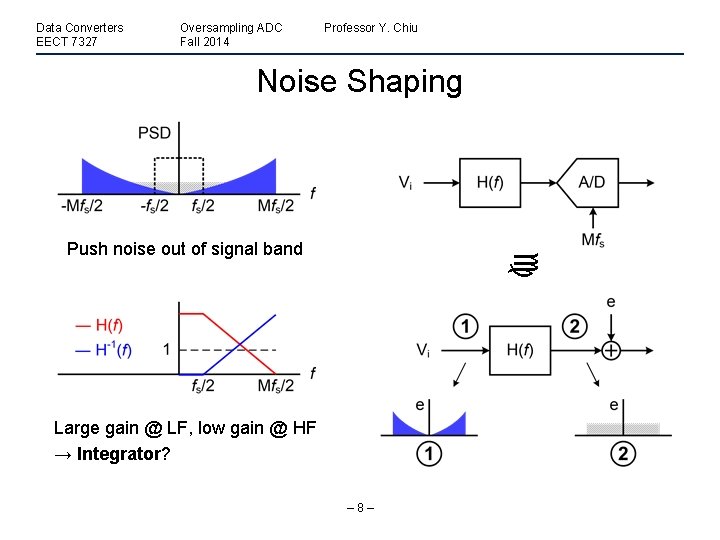
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Noise Shaping Push noise out of signal band Large gain @ LF, low gain @ HF → Integrator? – 8–

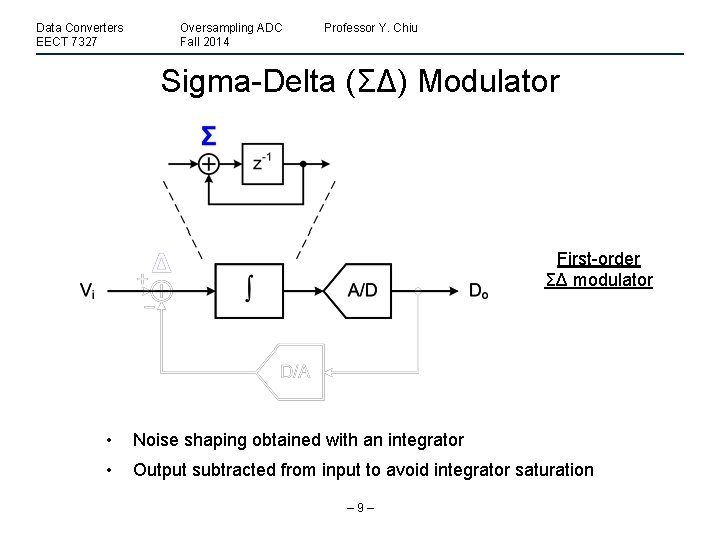
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Sigma-Delta (ΣΔ) Modulator First-order ΣΔ modulator • Noise shaping obtained with an integrator • Output subtracted from input to avoid integrator saturation – 9–

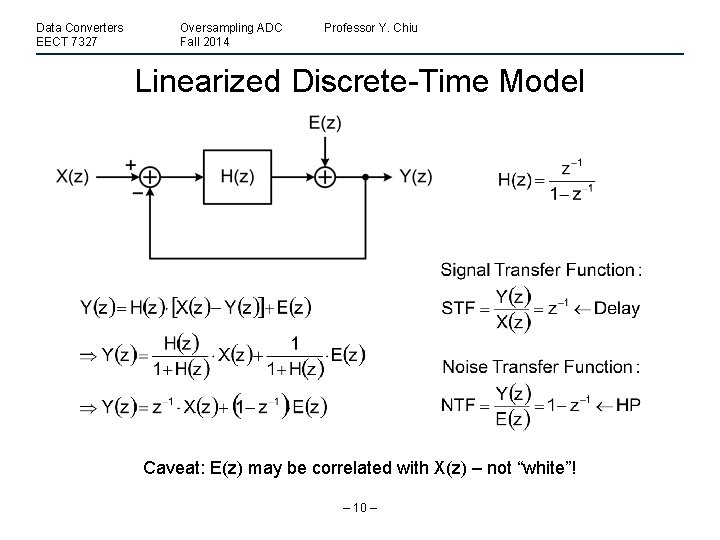
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Linearized Discrete-Time Model Caveat: E(z) may be correlated with X(z) – not “white”! – 10 –

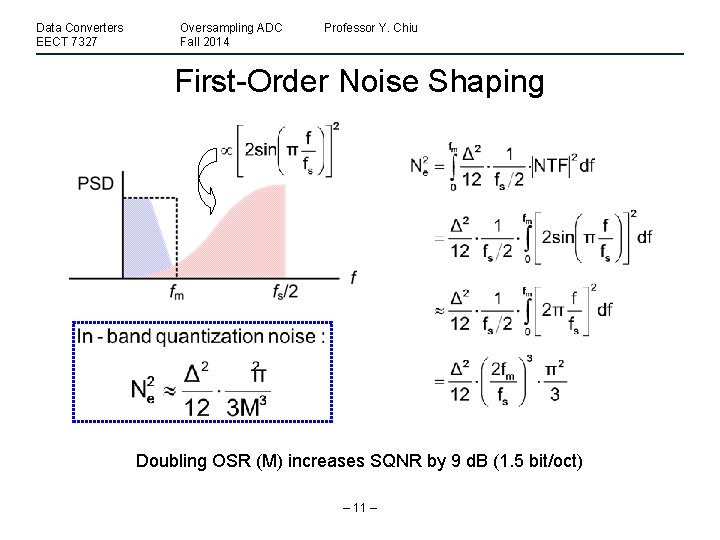
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu First-Order Noise Shaping Doubling OSR (M) increases SQNR by 9 d. B (1. 5 bit/oct) – 11 –

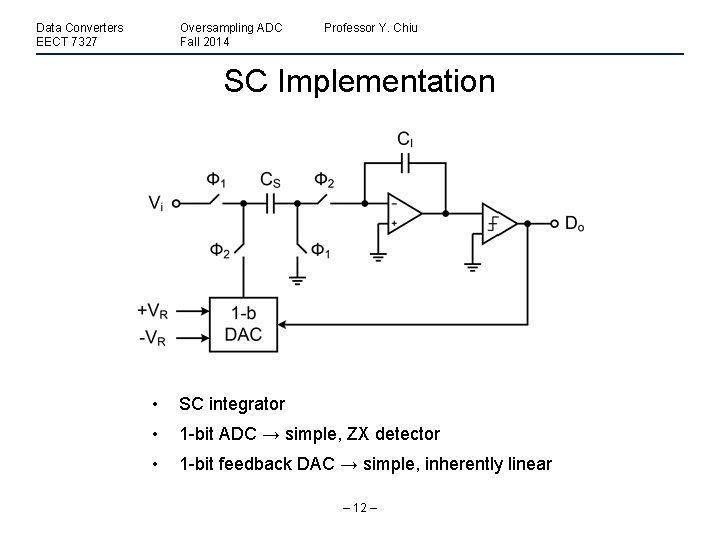
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu SC Implementation • SC integrator • 1 -bit ADC → simple, ZX detector • 1 -bit feedback DAC → simple, inherently linear – 12 –

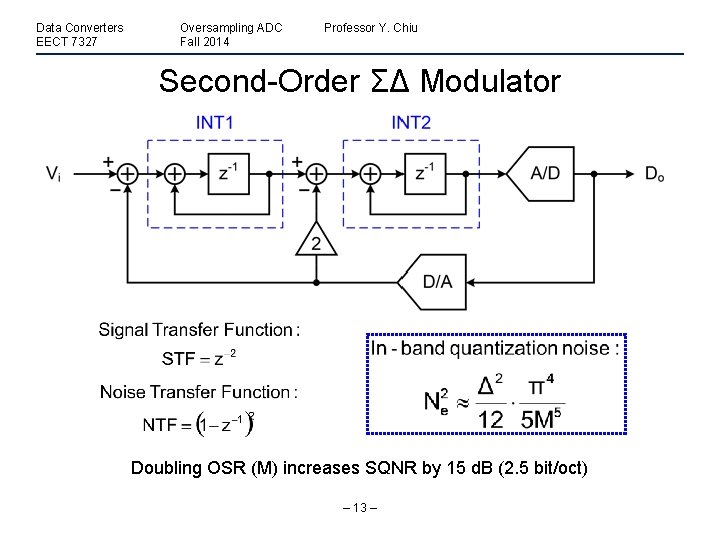
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Second-Order ΣΔ Modulator Doubling OSR (M) increases SQNR by 15 d. B (2. 5 bit/oct) – 13 –

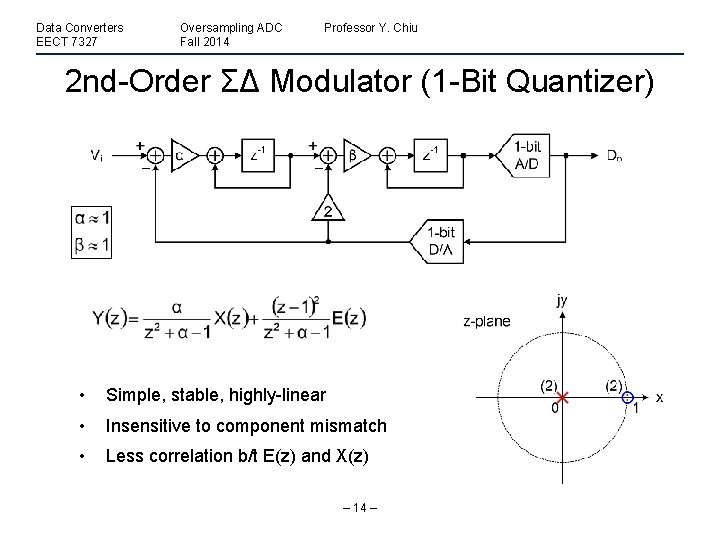
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu 2 nd-Order ΣΔ Modulator (1 -Bit Quantizer) • Simple, stable, highly-linear • Insensitive to component mismatch • Less correlation b/t E(z) and X(z) – 14 –

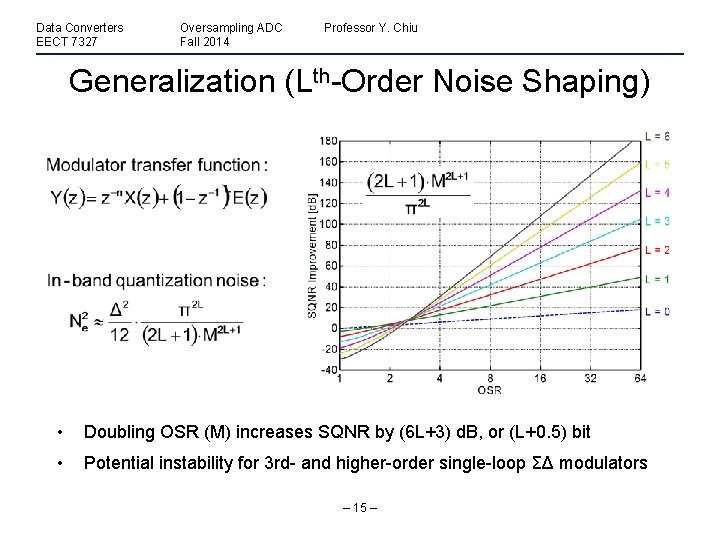
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Generalization (Lth-Order Noise Shaping) • Doubling OSR (M) increases SQNR by (6 L+3) d. B, or (L+0. 5) bit • Potential instability for 3 rd- and higher-order single-loop ΣΔ modulators – 15 –

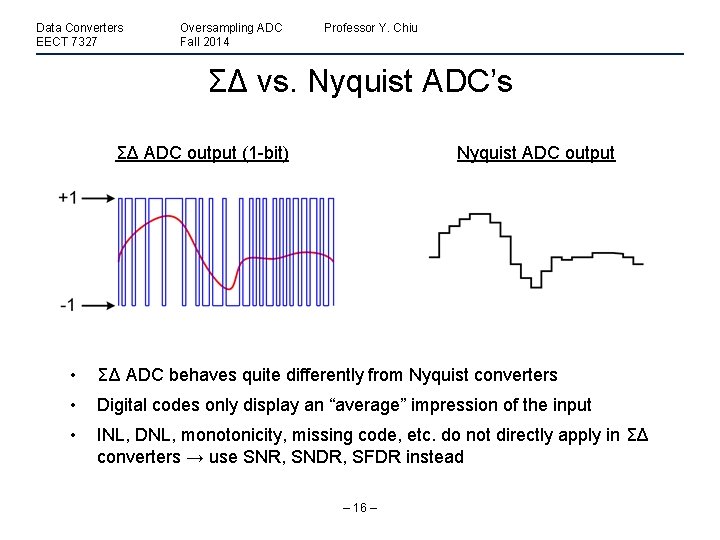
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu ΣΔ vs. Nyquist ADC’s ΣΔ ADC output (1 -bit) Nyquist ADC output • ΣΔ ADC behaves quite differently from Nyquist converters • Digital codes only display an “average” impression of the input • INL, DNL, monotonicity, missing code, etc. do not directly apply in ΣΔ converters → use SNR, SNDR, SFDR instead – 16 –

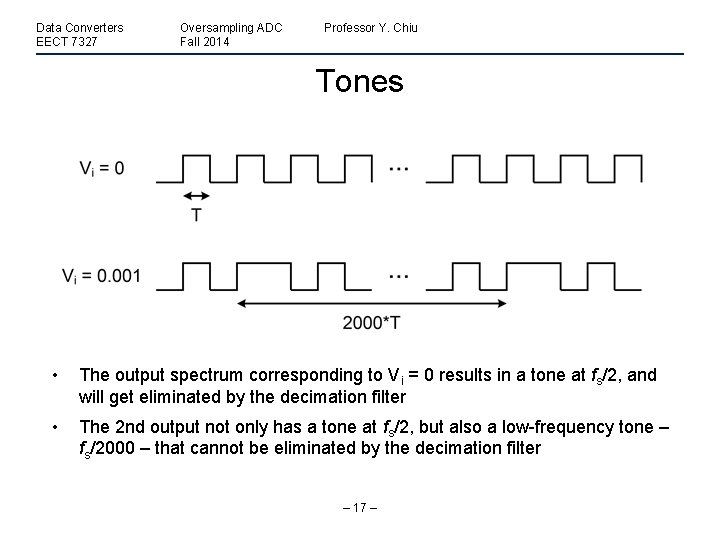
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Tones • The output spectrum corresponding to Vi = 0 results in a tone at fs/2, and will get eliminated by the decimation filter • The 2 nd output not only has a tone at fs/2, but also a low-frequency tone – fs/2000 – that cannot be eliminated by the decimation filter – 17 –

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Tones • Origin – the quantization error spectrum of the low-resolution ADC (1 -bit in the previous example) in a ΣΔ modulator is NOT white, but correlated with the input signal, especially for idle (DC) inputs. (R. Gray, “Spectral analysis of sigma-delta quantization noise”) • Approaches to “whitening” the error spectrum – Dither – high-frequency noise added in the loop to randomize the quantization error. Drawback is that large dither consumes the input dynamic range. – Multi-level quantization. Needs linear multi-level DAC. – High-order single-loop ΣΔ modulator. Potentially unstable. – Cascaded (MASH) ΣΔ modulator. Sensitive to mismatch. – 18 –

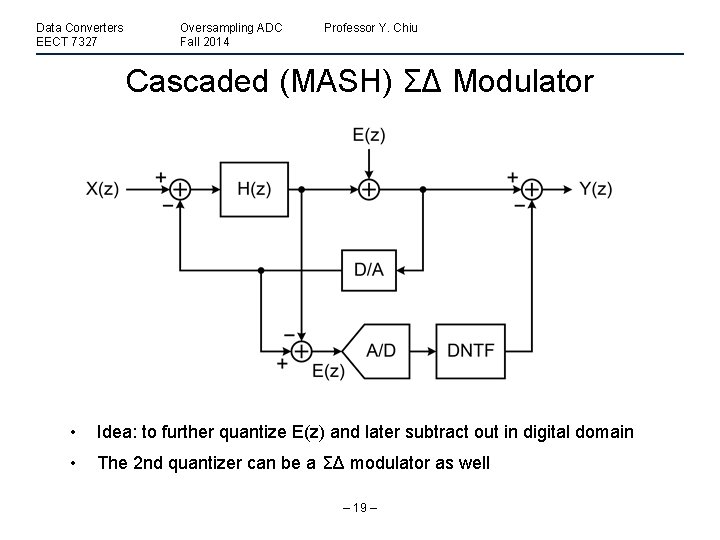
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Cascaded (MASH) ΣΔ Modulator • Idea: to further quantize E(z) and later subtract out in digital domain • The 2 nd quantizer can be a ΣΔ modulator as well – 19 –

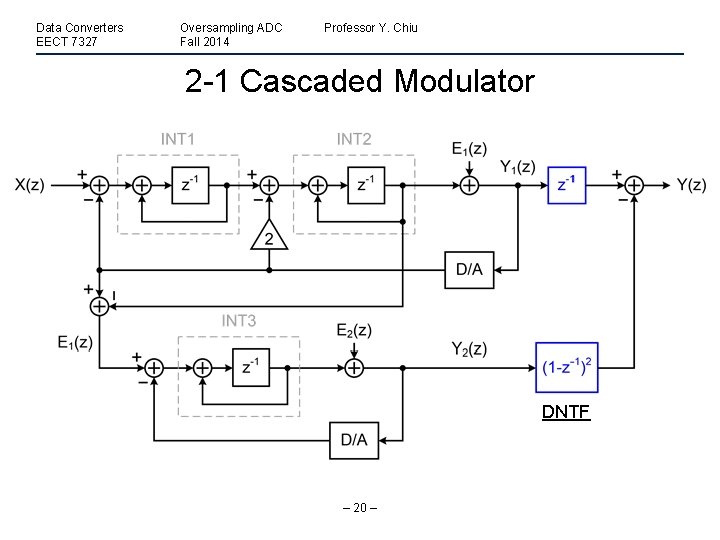
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu 2 -1 Cascaded Modulator DNTF – 20 –

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu 2 -1 Cascaded Modulator • E 1(z) completely cancelled assuming perfect matching between the modulator NTF (analog domain) and the DNTF (digital domain) • A 3 rd-order noise shaping on E 2(z) obtained • No potential instability problem – 21 –

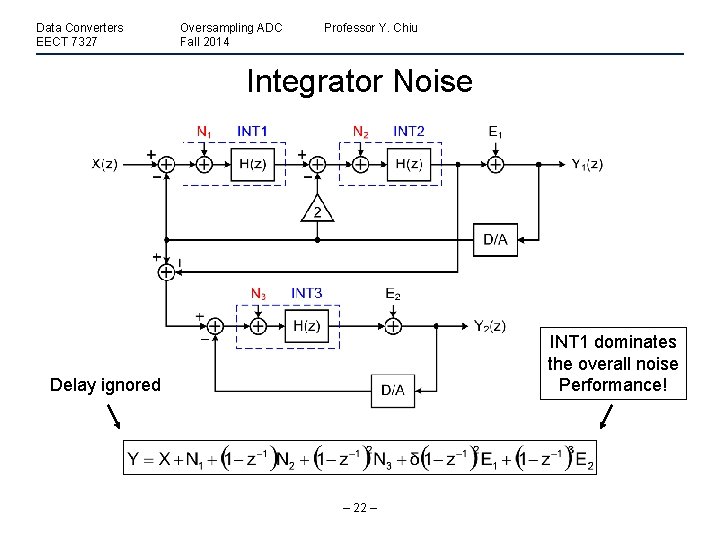
Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu Integrator Noise INT 1 dominates the overall noise Performance! Delay ignored – 22 –

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu References 1. B. E. Boser and B. A. Wooley, JSSC, pp. 1298 -1308, issue 6, 1988. 2. B. H. Leung et al. , JSSC, pp. 1351 -1357, issue 6, 1988. 3. T. C. Leslie and B. Singh, ISCAS, 1990, pp. 372 -375. 4. B. P. Brandt and B. A. Wooley, JSSC, pp. 1746 -1756, issue 12, 1991. 5. F. Chen and B. H. Leung, JSSC, pp. 453 -460, issue 4, 1995. 6. R. T. Baird and T. S. Fiez, TCAS 2, pp. 753 -762, issue 12, 1995. 7. T. L. Brooks et al. , JSSC, pp. 1896 -1906, issue 12, 1997. 8. A. K. Ong and B. A. Wooley, JSSC, pp. 1920 -1934, issue 12, 1997. 9. S. A. Jantzi, K. W. Martin, and A. S. Sedra, JSSC, pp. 1935 -1950, issue 12, 1997. 10. A. Yasuda, H. Tanimoto, and T. Iida, JSSC, pp. 1879 -1886, issue 12, 1998. 11. A. R. Feldman, B. E. Boser, and P. R. Gray, JSSC, pp. 1462 -1469, issue 10, 1998. 12. H. Tao and J. M. Khoury, JSSC, pp. 1741 -1752, issue 12, 1999. 13. E. J. van der Zwan et al. , JSSC, pp. 1810 -1819, issue 12, 2000. 14. I. Fujimori et al. , JSSC, pp. 1820 -1828, issue 12, 2000. 15. Y. Geerts, M. S. J. Steyaert, W. Sansen, JSSC, pp. 1829 -1840, issue 12, 2000. – 23 –

Data Converters EECT 7327 Oversampling ADC Fall 2014 Professor Y. Chiu References 16. T. Burger and Q. Huang, JSSC, pp. 1868 -1878, issue 12, 2001. 17. K. Vleugels, S. Rabii, and B. A. Wooley, JSSC, pp. 1887 -1899, issue 12, 2001. 18. S. K. Gupta and V. Fong, JSSC, pp. 1653 -1661, issue 12, 2002. 19. R. Schreier et al. , JSSC, pp. 1636 -1644, issue 12, 2002. 20. J. Silva et al. , CICC, 2002, pp. 183 -190. 21. Y. -I. Park et al. , CICC, 2003, pp. 115 -118. 22. L. J. Breems et al. , JSSC, pp. 2152 -2160, issue 12, 2004. 23. R. Jiang and T. S. Fiez, JSSC, pp. 63 -74, issue 12, 2004. 24. P. Balmelli and Q. Huang, JSSC, pp. 2161 -2169, issue 12, 2004. 25. K. Y. Nam et al. , CICC, 2004, pp. 515 -518. 26. X. Wang et al. , CICC, 2004, pp. 523 -526. 27. A. Bosi et al. , ISSCC, 2005, pp. 174 -175. 28. N. Yaghini and D. Johns, ISSCC, 2005, pp. 502 -503. 29. G. Mitteregger et al. , JSSC, pp. 2641 -2649, issue 12, 2006. 30. R. Schreier et al. , JSSC, pp. 2632 -2640, issue 12, 2006. – 24 –