Data Compression Engineering Math Physics EMP Steve Lyon

Data Compression Engineering Math Physics (EMP) Steve Lyon Electrical Engineering 1

Why Compress? • Digital information is represented in bits – Text: characters (each encoded as a number) – Audio: sound samples – Image: pixels • More bits means more resources – Storage (e. g. , memory or disk space) – Bandwidth (e. g. , time to transmit over a link) • Compression reduces the number of bits – Use less storage space (or store more items) – Use less bandwidth (or transmit faster) – Cost is increased processing time/CPU hardware 2

Do we really need to compress? • Video – TV – 640 x 480 pixels (ideal US broadcast TV) – 3 colors/pixel (Red, Green, Blue) – 1 byte (values from 0 to 255) for each color ~900, 000 bytes per picture (frame) – 30 frames/second ~27 MB/sec – DVD holds ~5 GB Can store ~3 minutes of uncompressed video on a DVD Must compress 3

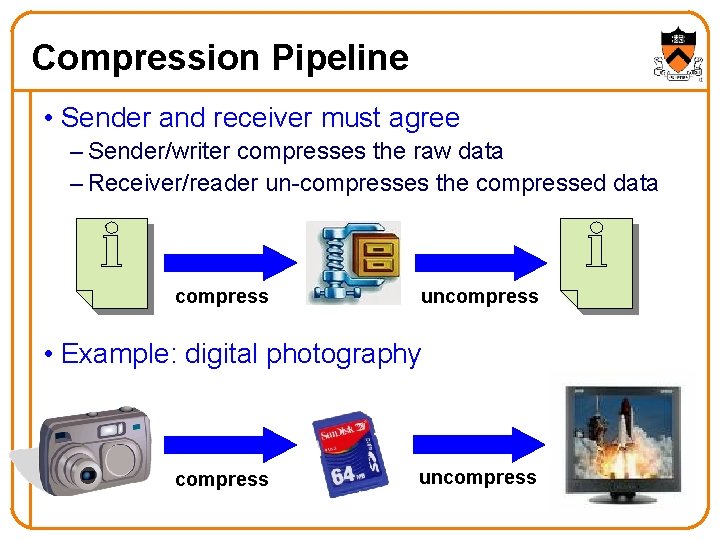
Compression Pipeline • Sender and receiver must agree – Sender/writer compresses the raw data – Receiver/reader un-compresses the compressed data compress uncompress • Example: digital photography compress uncompress 4

Two Kinds of Compression • Lossless – Only exploits redundancy in the data – So, the data can be reconstructed exactly – Necessary for most text documents (e. g. , legal documents, computer programs, and books) • Lossy – Exploits both data redundancy and human perception – So, some of the information is lost forever – Acceptable for digital audio, images, and video 5

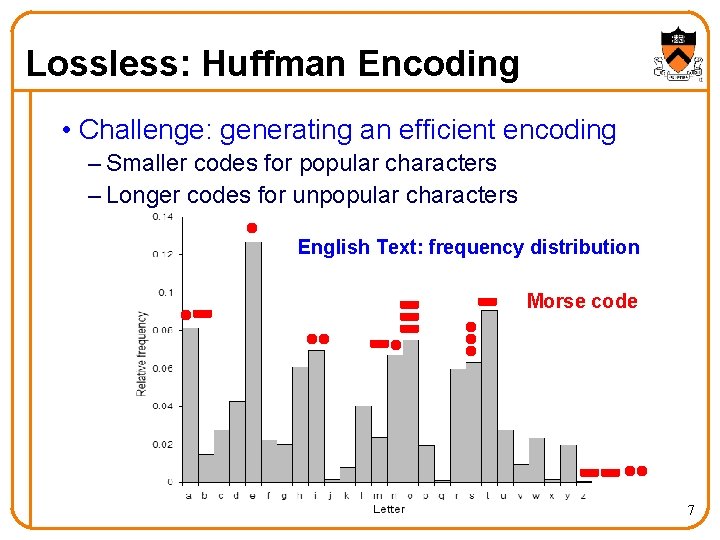
Lossless: Huffman Encoding • Normal encoding of text – Fixed number of bits for each character • ASCII with seven bits for each character – Allows representation of 27=128 characters – Use 97 for ‘a’, 98 for ‘b’, …, 122 for ‘z’ • But, some characters occur more often than others – Letter ‘a’ occurs much more often than ‘x’ • Idea: assign fewer bits to more-popular symbols – Encode ‘a’ as “ 000” – Encode ‘x’ as “ 11010111” 6

Lossless: Huffman Encoding • Challenge: generating an efficient encoding – Smaller codes for popular characters – Longer codes for unpopular characters English Text: frequency distribution Morse code 7

Lossless: Run-Length Encoding • Sometimes the same symbol repeats – Such as “eeeeeee” or “eeeeetnnnnnn” – That is, a run of “e” symbols or a run of “n” symbols • Idea: capture the symbol only once – Count the number of times the symbol occurs – Record the symbol and the number of occurrences • Examples – So, “eeeeeee” becomes “@e 7” – So, “eeeeetnnnnnn” becomes “@e 5 t@n 6” • Useful for fax machines – Lots of white, separate by occasional black 8

Image Compression • Benefits of reducing the size – Consume less storage space and network bandwidth – Reduce the time to load, store, and transmit the image • Redundancy in the image – Neighboring pixels often the same, or at least similar – E. g. , the blue sky • Human perception factors – Human eye is not sensitive to high spatial frequencies 9

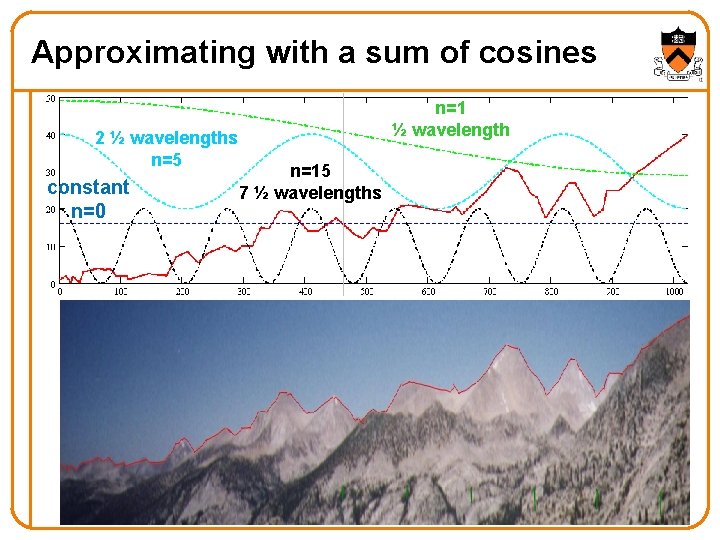
Approximating arbitrary functions (curves) How can we represent some arbitrary function by some simple ones? Ex. This mountain range

Approximating with a sum of cosines 2 ½ wavelengths n=5 constant n=0 n=1 ½ wavelength n=15 7 ½ wavelengths

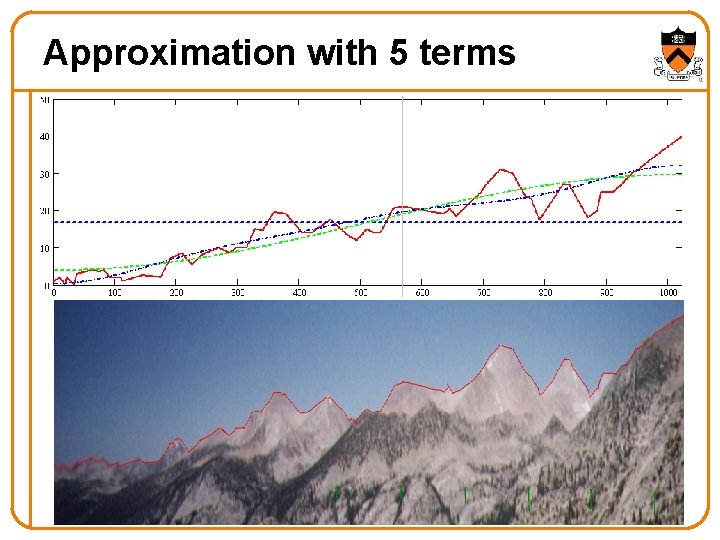
Approximation with 5 terms

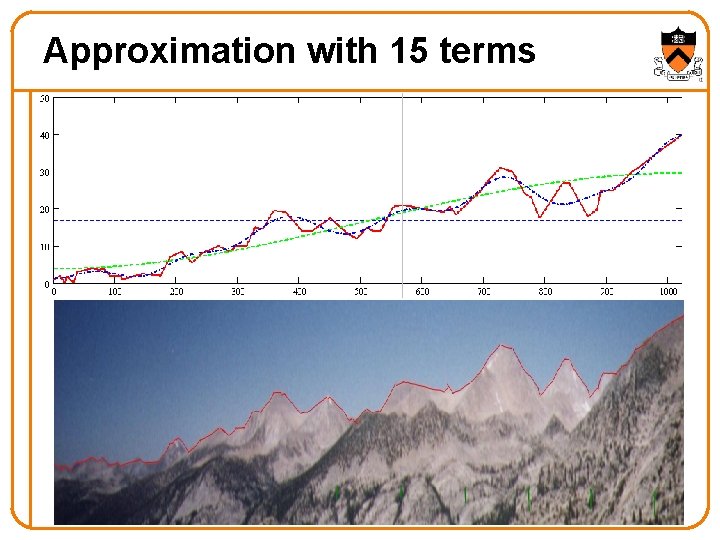
Approximation with 15 terms

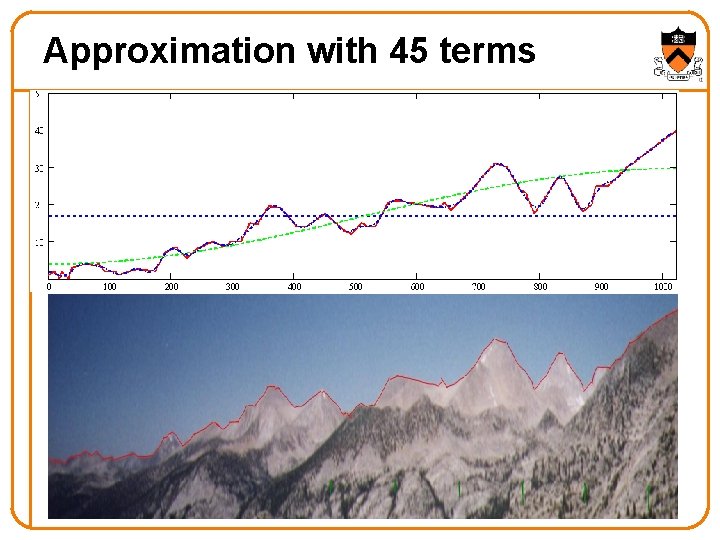
Approximation with 45 terms

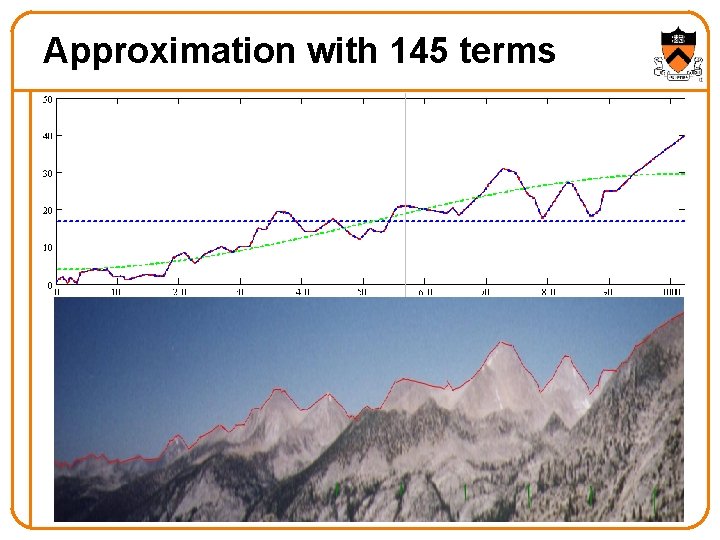
Approximation with 145 terms

Discrete cosine transform • How do we determine the coefficients of each term? – How much of “ 3 wavelengths” vs. “ 47 wavelengths”? – Look at the fit and tweak the coefficients? – Maybe for a couple – Insane for 145 • Idea: look at • = 0 if n m • = /2 if n = m (or if n = m = 0) • So, if • Then 16

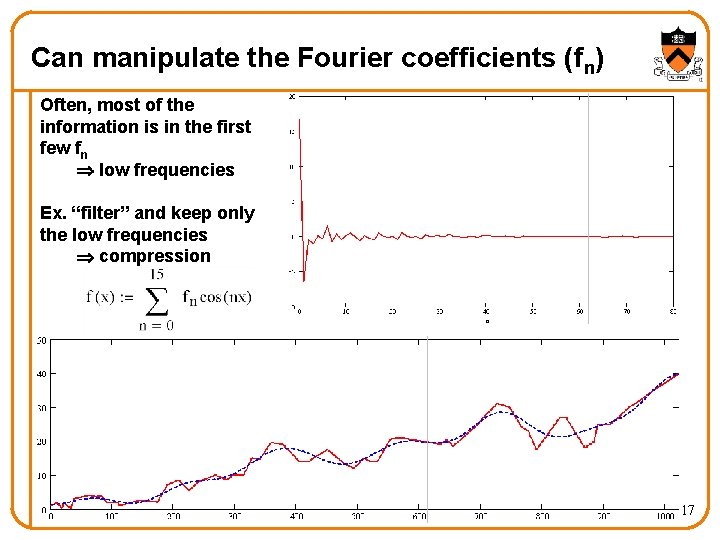
Can manipulate the Fourier coefficients (fn) Often, most of the information is in the first few fn low frequencies Ex. “filter” and keep only the low frequencies compression 17

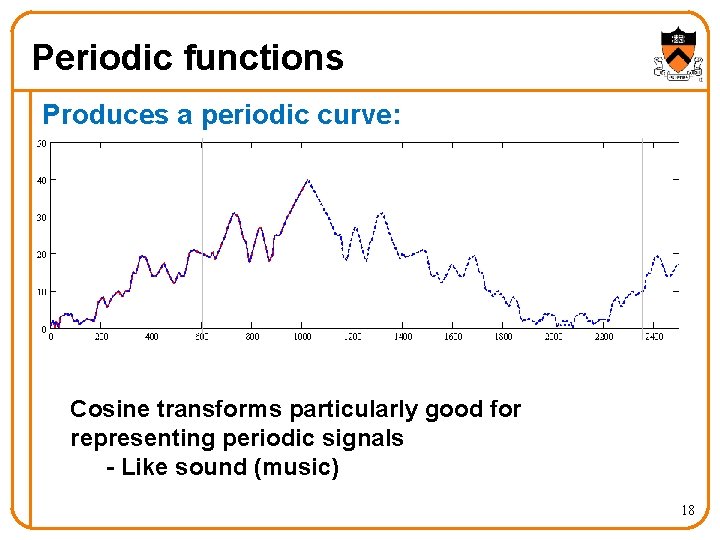
Periodic functions Produces a periodic curve: Cosine transforms particularly good for representing periodic signals - Like sound (music) 18

Example: Digital Audio • Sampling the analog signal – Sample at some fixed rate – Each sample is an arbitrary real number • Quantizing each sample – Round each sample to one of a finite number of values – Represent each sample in a fixed number of bits 4 bit representation (values 0 -15) 19

Example: Digital Audio • Speech – Sampling rate: 8000 samples/second – Sample size: 8 bits per sample – Rate: 64 kbps • Compact Disc (CD) – Sampling rate: 44, 100 samples/second – Sample size: 16 bits per sample – Rate: 705. 6 kbps for mono, 1. 411 Mbps for stereo 20

Example: Digital Audio • Audio data requires too much bandwidth – Speech: 64 kbps is too high for a dial-up modem user – Stereo music: 1. 411 Mbps exceeds most access rates • Compression to reduce the size – Remove redundancy – Remove details that humans tend not to perceive • Example audio formats – Speech: GSM (13 kbps), G. 729 (8 kbps), and G. 723. 3 (6. 4 and 5. 3 kbps) – Stereo music: MPEG 1 layer 3 (MP 3) at 96 kbps, 128 kbps, and 160 kbps 21

Joint Photographic Experts Group (JPEG) 108 KB 34 KB Lossy compression 22

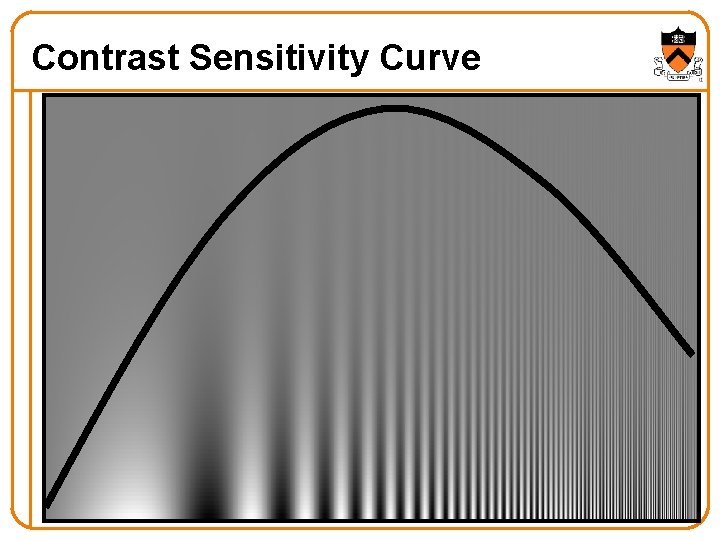
Contrast Sensitivity Curve 23

How JPEG works 1 • Digital cameras (CCDs) output RGB – Eyes most sensitive to intensity – Less sensitive to color variations • Convert image to YCb. Cr – Y = intensity ~ (R+G+B) Gives black & white B&W TV’s could use that when color TV first came out – Cb ~ (B – Y) – Cr ~ (R – Y) • Sometimes leave as RGB – gives poorer quality jpeg 24

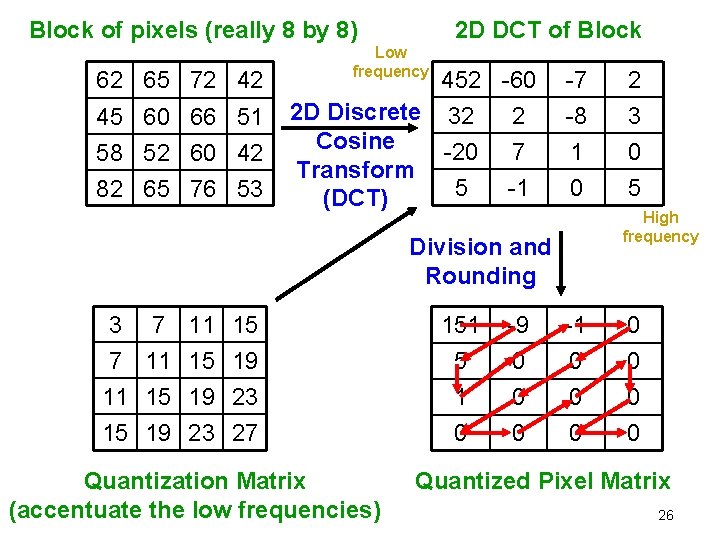
How JPEG works 2 • Either RGB or YCb. Cr gives 3 8 -bit “planes” – Process separately • Process image in 8 -pixel x 8 -pixel blocks – 2 -dimensional discrete Fourier Transform (DCT) N 1 = N 2 = 8 – Just matrix multiplication – Produces 8 x 8 matrix (B) of spatial frequencies – “Quantize” divide each element by fixed number High-frequency coefficients divided by larger number If result is small, set to 0 (the lossy part) Can be “lossier” on Cb and Cr than on Y • Lossless compression to squeeze out the 0’s 25

Block of pixels (really 8 by 8) 62 65 72 42 45 60 66 51 58 52 60 42 82 65 76 53 2 D DCT of Block Low frequency 452 -60 2 D Discrete 32 2 Cosine -20 7 Transform 5 -1 (DCT) -7 -8 1 0 High frequency Division and Rounding 3 7 11 15 19 23 27 Quantization Matrix (accentuate the low frequencies) 151 5 1 0 -9 0 0 0 2 3 0 5 -1 0 0 0 0 Quantized Pixel Matrix 26

JPEG Artifacts Ø JPEG does not compress text or diagrams well. Ø Here same file size as lossless compression – gif Ø Get “halos” around letters, lines, etc. Ø Lines and text have sharp edges Ø JPEG smears Ø Get “blotchy” appearance when heavily compressed Ø Have 8 x 8 blocks of all one color – only constant term in DCT remained 27

Conclusion • “Raw” digital information often has many more bits than necessary – Redundancies and patterns we can use – Information that is imperceptible to people • Lossless compression – Used when must be able to exactly recreate original – Find common patterns (letter frequencies, repeats, etc. ) • Lossy Compression – Can get very large compression ratios – a few to 1000’s – Exploit redundancy and human perception Remove information we (people) don’t need – Too much compression degrades the signals 28