Data Collection and Analysis Area Measurement How to

Data Collection and Analysis Area Measurement How to measure the perimeter and area of an arbitrary closed shape?

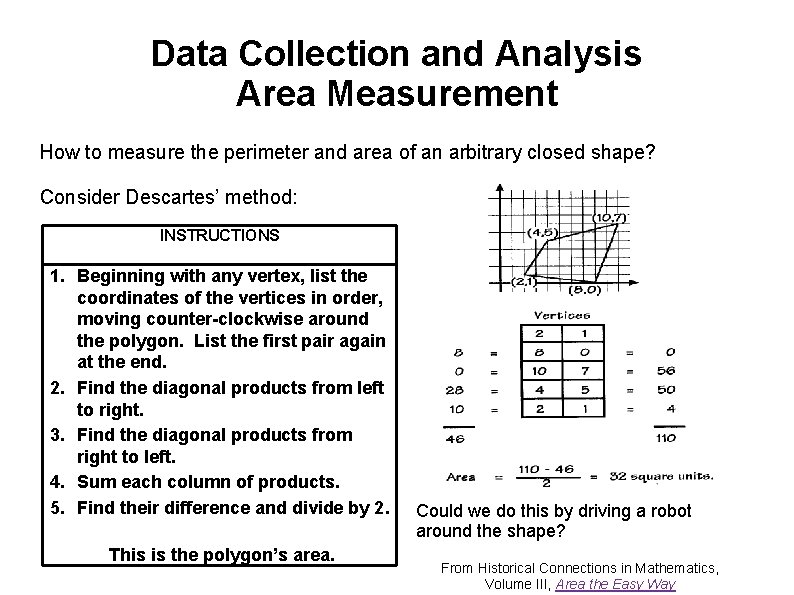
Data Collection and Analysis Area Measurement How to measure the perimeter and area of an arbitrary closed shape? Consider Descartes’ method: INSTRUCTIONS 1. Beginning with any vertex, list the coordinates of the vertices in order, moving counter-clockwise around the polygon. List the first pair again at the end. 2. Find the diagonal products from left to right. 3. Find the diagonal products from right to left. 4. Sum each column of products. 5. Find their difference and divide by 2. This is the polygon’s area. Could we do this by driving a robot around the shape? From Historical Connections in Mathematics, Volume III, Area the Easy Way

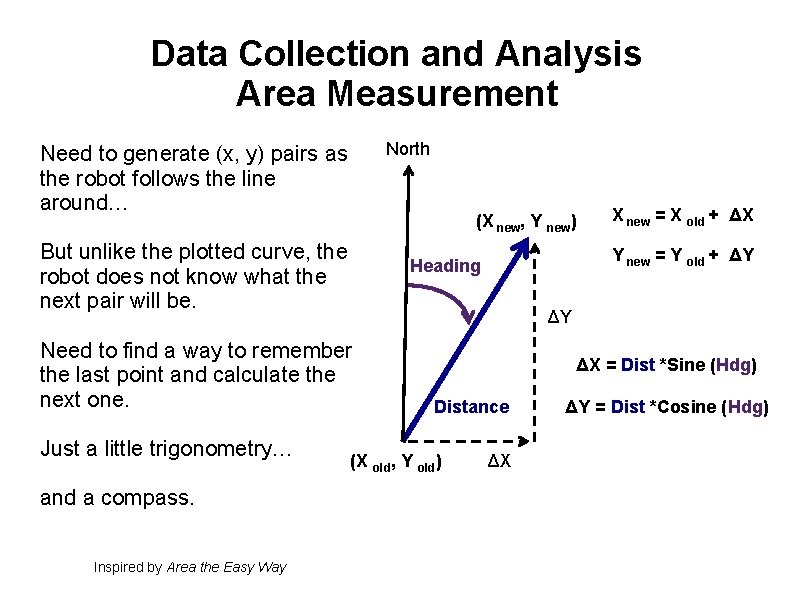
Data Collection and Analysis Area Measurement North Need to generate (x, y) pairs as the robot follows the line around… (X new, Y new) But unlike the plotted curve, the robot does not know what the next pair will be. and a compass. Inspired by Area the Easy Way Y new = Y old + ΔY Heading ΔY Need to find a way to remember the last point and calculate the next one. Just a little trigonometry… X new = X old + ΔX ΔX = Dist *Sine (Hdg) Distance (X old, Y old) ΔX ΔY = Dist *Cosine (Hdg)

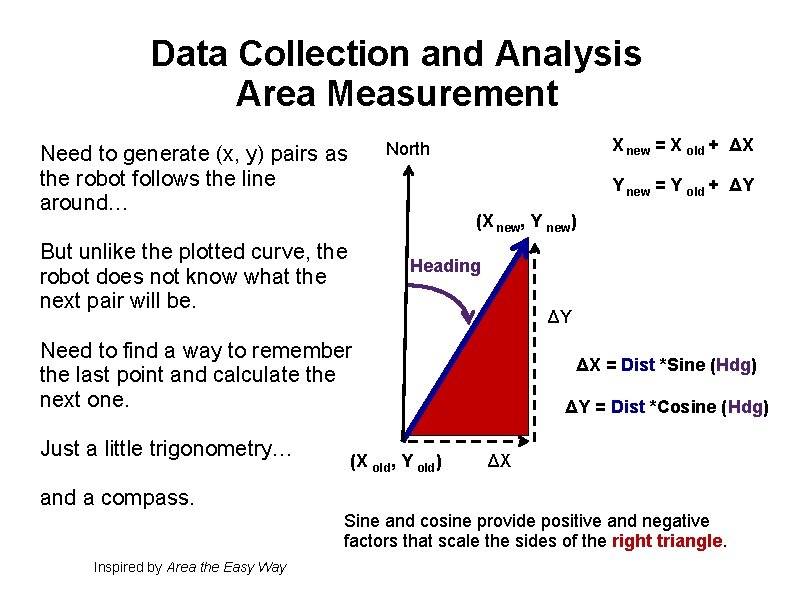
Data Collection and Analysis Area Measurement Y new = Y old + ΔY (X new, Y new) But unlike the plotted curve, the robot does not know what the next pair will be. Heading ΔY Need to find a way to remember the last point and calculate the next one. Just a little trigonometry… X new = X old + ΔX North Need to generate (x, y) pairs as the robot follows the line around… ΔX = Dist *Sine (Hdg) Distance (X old, Y old) ΔY = Dist *Cosine (Hdg) ΔX and a compass. Sine and cosine provide positive and negative factors that scale the sides of the right triangle. Inspired by Area the Easy Way

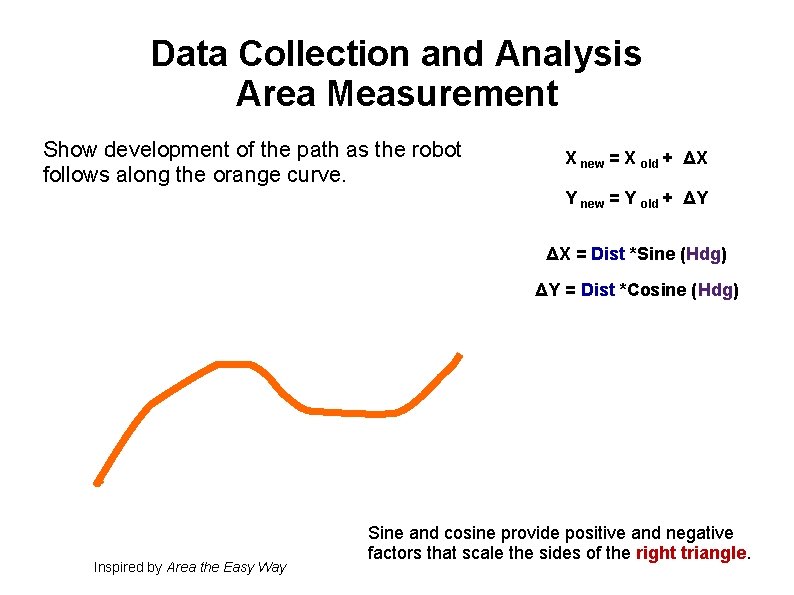
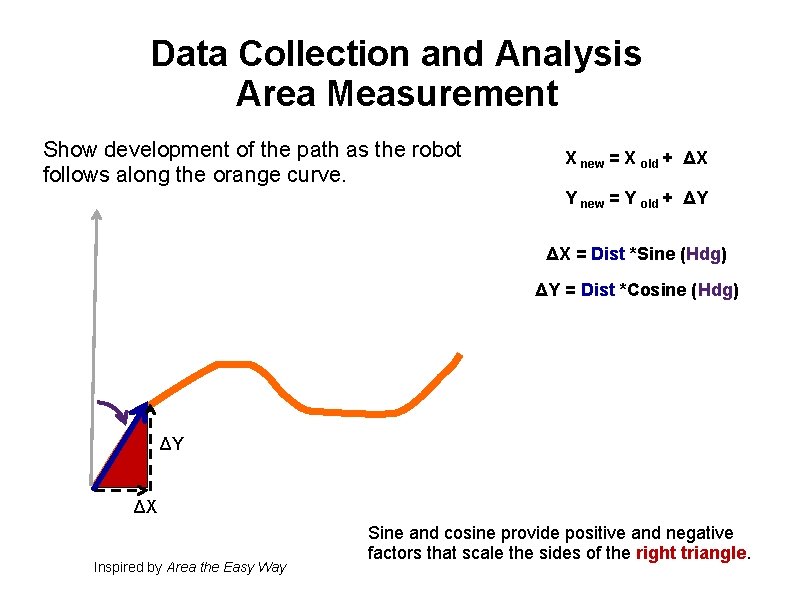
Data Collection and Analysis Area Measurement Show development of the path as the robot follows along the orange curve. X new = X old + ΔX Y new = Y old + ΔY ΔX = Dist *Sine (Hdg) ΔY = Dist *Cosine (Hdg) Inspired by Area the Easy Way Sine and cosine provide positive and negative factors that scale the sides of the right triangle.

Data Collection and Analysis Area Measurement Show development of the path as the robot follows along the orange curve. X new = X old + ΔX Y new = Y old + ΔY ΔX = Dist *Sine (Hdg) ΔY = Dist *Cosine (Hdg) ΔY ΔX Inspired by Area the Easy Way Sine and cosine provide positive and negative factors that scale the sides of the right triangle.

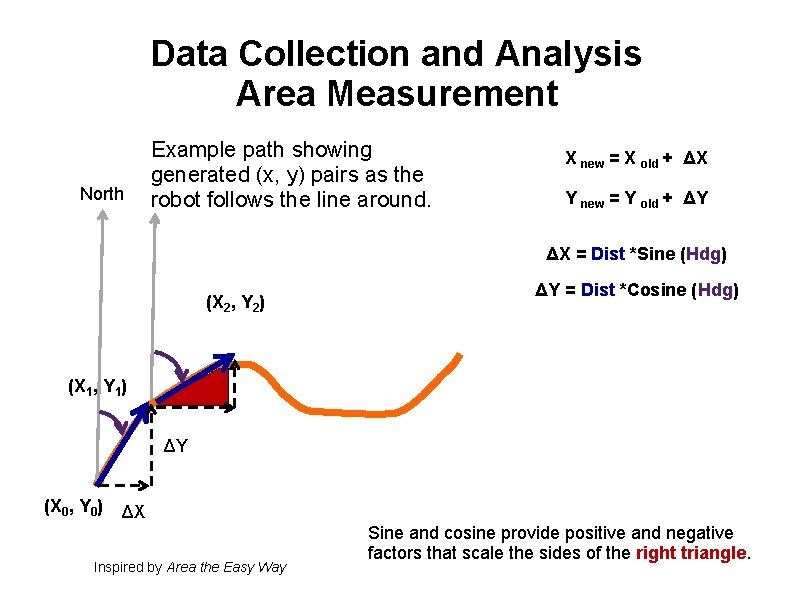
Data Collection and Analysis Area Measurement North Example path showing generated (x, y) pairs as the robot follows the line around. X new = X old + ΔX Y new = Y old + ΔY ΔX = Dist *Sine (Hdg) (X 2, Y 2) ΔY = Dist *Cosine (Hdg) (X 1, Y 1) ΔY (X 0, Y 0) ΔX Inspired by Area the Easy Way Sine and cosine provide positive and negative factors that scale the sides of the right triangle.

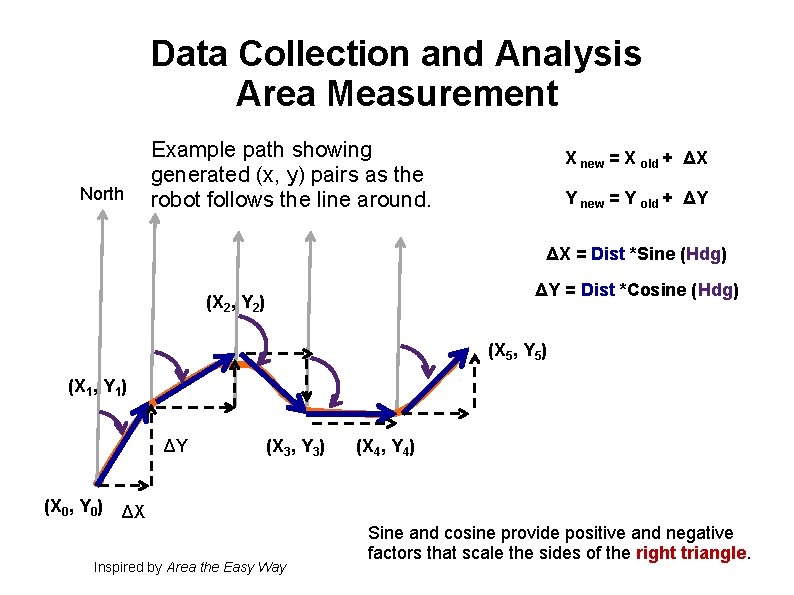
Data Collection and Analysis Area Measurement North Example path showing generated (x, y) pairs as the robot follows the line around. X new = X old + ΔX Y new = Y old + ΔY ΔX = Dist *Sine (Hdg) ΔY = Dist *Cosine (Hdg) (X 2, Y 2) (X 5, Y 5) (X 1, Y 1) ΔY (X 0, Y 0) (X 3, Y 3) (X 4, Y 4) ΔX Inspired by Area the Easy Way Sine and cosine provide positive and negative factors that scale the sides of the right triangle.

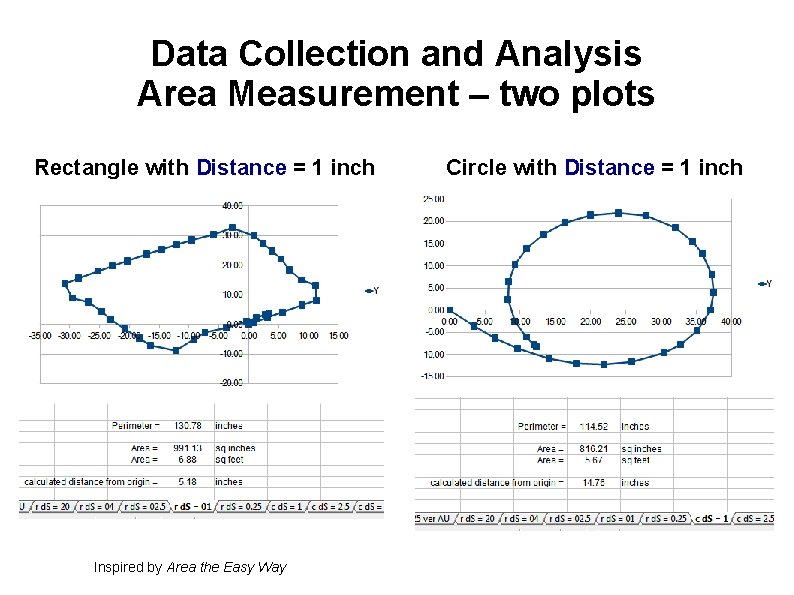
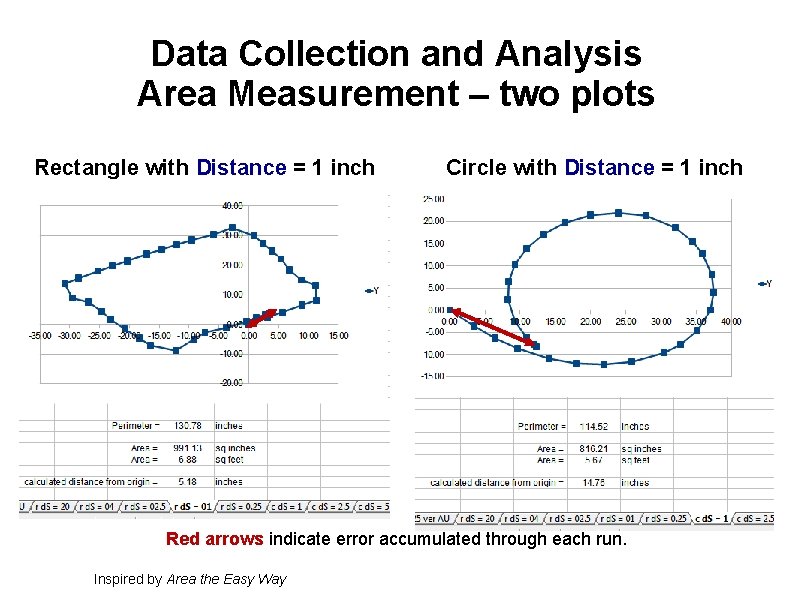
Data Collection and Analysis Area Measurement – two plots Rectangle with Distance = 1 inch Inspired by Area the Easy Way Circle with Distance = 1 inch

Data Collection and Analysis Area Measurement – two plots Rectangle with Distance = 1 inch Circle with Distance = 1 inch Red arrows indicate error accumulated through each run. Inspired by Area the Easy Way

Data Collection and Analysis Area Measurement