Data classification using geostatistical hierarchical clustering for robust

Data classification using geostatistical hierarchical clustering for robust and dynamic domaining Christianne MARIZ, Laurent WAGNER

WHAT IS DATA CLASSIFICATION? • Also called Sample Clustering or Clustering; • Purpose: To classify samples into geological domains; • Corresponds to the first step of the geological modeling process, it prepares your data to implicit modeling; • Usually a fastidious and fairly subjective step.

DATA CLASSIFICATION Innovative methodologies for data classification: • Geostatistical Hierarchical Clustering (GHC): machine learning algorithm • Hybrid Classification: combination of two algorithms – Geostatistical Hierarchical Clustering; and – Support Vector Machine.

GEOSTATISTICAL HIERARCHICAL CLUSTERING (GHC) • Multivariate unsupervised machine learning algorithm which provides a sample classification into domains, respecting data connectivity and similarity; • Combines geological and statistical concepts; • Controls: • Anisotropies ; • Weight on variables (Similarity Function) • Number of domains 5 ; • Post-processing tools: merge & smooth. 1 ; and

GEOSTATISTICAL HIERARCHICAL CLUSTERING (GHC) 1. Create a network; 2. Compute dissimilarity (Similarity Function) between linked samples; and 3. Merge gradually samples/clusters with a Linkage Criterion.

GEOSTATISTICAL HIERARCHICAL CLUSTERING (GHC) Dissimilarity function • Weighted Euclidian Distance

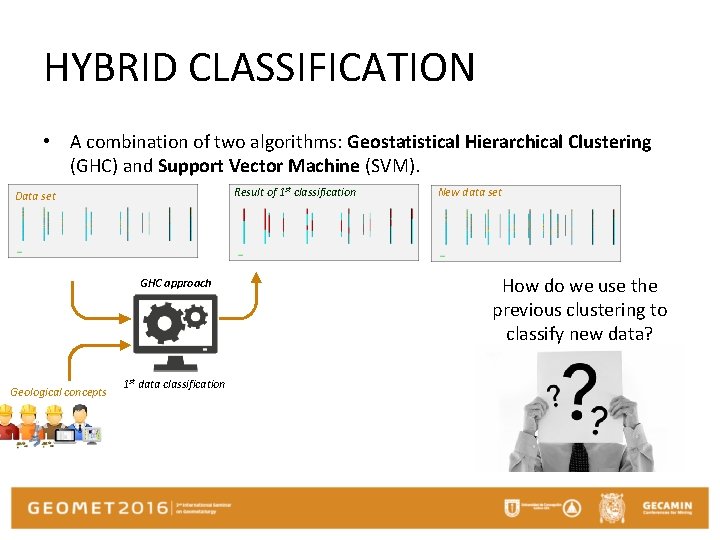
HYBRID CLASSIFICATION • A combination of two algorithms: Geostatistical Hierarchical Clustering (GHC) and Support Vector Machine (SVM). Result of 1 st classification Data set GHC approach Geological concepts 1 st data classification New data set How do we use the previous clustering to classify new data?

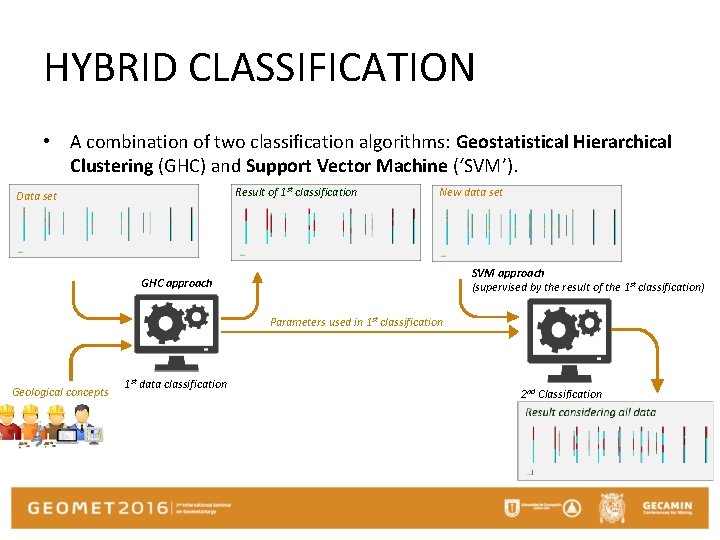
HYBRID CLASSIFICATION • A combination of two classification algorithms: Geostatistical Hierarchical Clustering (GHC) and Support Vector Machine (‘SVM’). Result of 1 st classification Data set New data set SVM approach (supervised by the result of the 1 st classification) GHC approach Parameters used in 1 st classification Geological concepts 1 st data classification 2 nd Classification

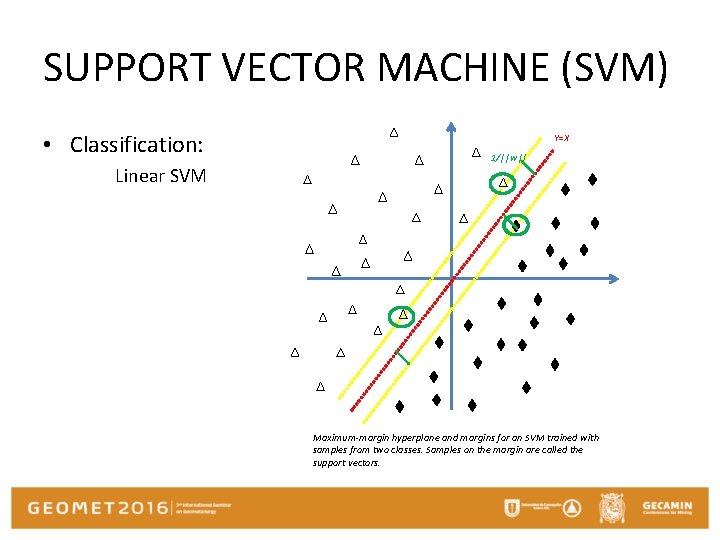
SUPPORT VECTOR MACHINE (SVM) • Classification: Linear SVM Y=X 1/||w|| Maximum-margin hyperplane and margins for an SVM trained with samples from two classes. Samples on the margin are called the support vectors.

CASE STUDY – REAL IRON MINE DATASET • Fe orebody in the Pilbara region; • Geology: BIF • Real data set provides by BHP Billiton: • • N 2. 120 vertical drill holes and 111. 842 samples; 15 variables: Fe, Ca. O, Al 2 O 3, Fe 2 P, K 2 O, Mg. O, Mn, Na 2 O, Si. O 2, Ti. O 2, Goethite, Hematite, Weathering, etc. Slump folding in Banded Ironstone Formation (BIF) in hand specimen from the Pilbara. Photo by Wout Nijman Harmersley Province-Pilbara Geological Sketch Map

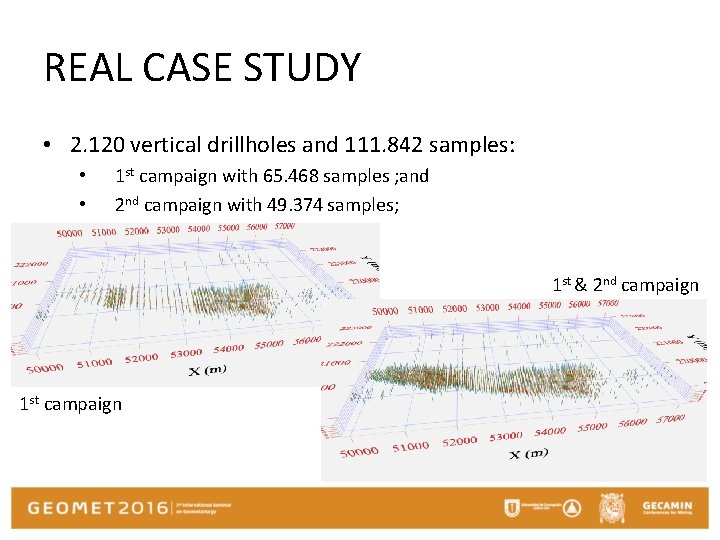
REAL CASE STUDY • 2. 120 vertical drillholes and 111. 842 samples: • • 1 st campaign with 65. 468 samples ; and 2 nd campaign with 49. 374 samples; 1 st & 2 nd campaign 1 st campaign

1 ST CAMPAIGN • Samples are classified using Geostatistical Hierarchical Clustering; • Parameters: – Pre-processing of very low grades; – Weights assigned: Variable Weight Fe 10 Al 2 O 3 5 Si. O 2 1 Hematite 1 Goethite 1 Weathering 1 – Anisotropies: – Post-processing to smooth the output.

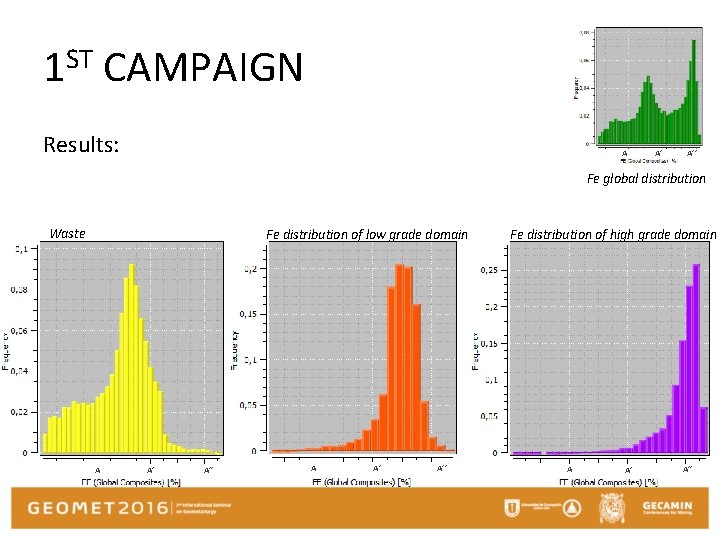
1 ST CAMPAIGN Results: A A’ A’’ Fe global distribution Waste Fe distribution of low grade domain A A’ A’’ Fe distribution of high grade domain A A’ A’’

1 ST & 2 ND CAMPAIGN Updating with new data set • Samples are classified using hybrid data classification: – Support Vector Machine (SVM) supervised by the result of the first classification (GHC); • Parameters are the same as the first campaign.

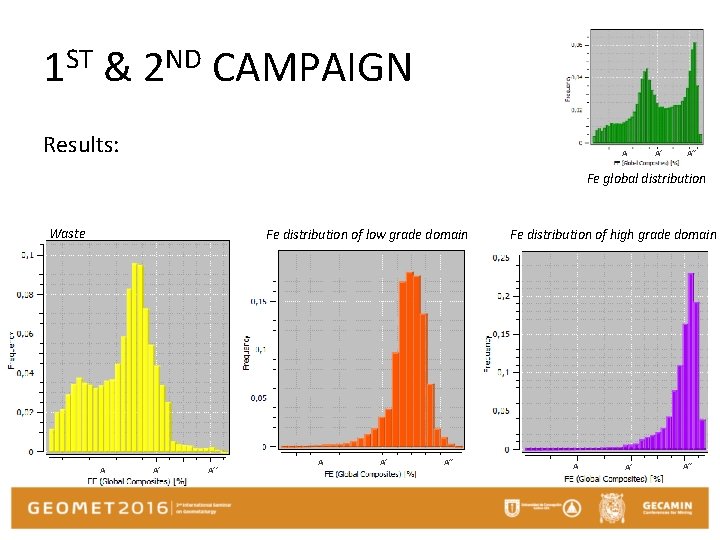
1 ST & 2 ND CAMPAIGN Results: A A’ A’’ Fe global distribution Waste Fe distribution of low grade domain A A’ A’’ Fe distribution of high grade domain A A’ A’’

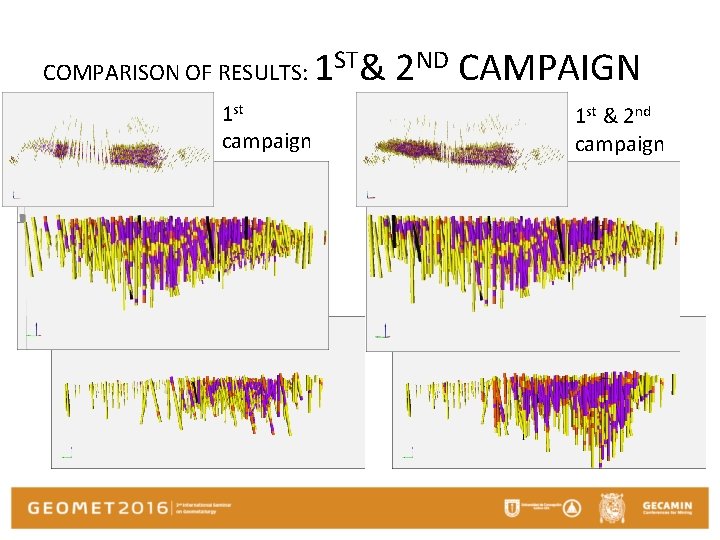
COMPARISON OF RESULTS: 1 st campaign 1 ST& 2 ND CAMPAIGN 1 st & 2 nd campaign

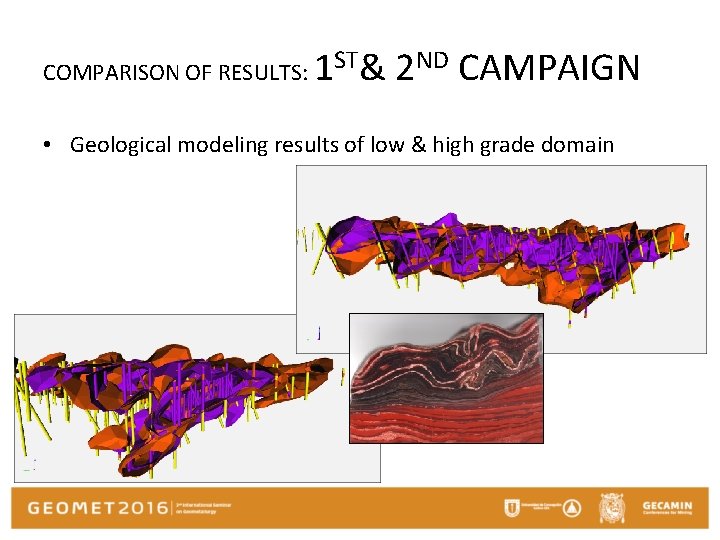
COMPARISON OF RESULTS: 1 ST& 2 ND CAMPAIGN • Geological modeling results of low & high grade domain

CONCLUSION • Geostatistical Hierarchical Clustering algorithm and Hybrid Classification approach: – Objective sample flagging based on scientific criteria; – To take account the key spatial dependency between the samples; – Increase productivity; • Data classification updating: – Faster than traditional methods; – More flexible;

Bibliography • • Boser, B. E. ; Guyon, I. M. ; Vapnik, V. N. (1992). "A training algorithm for optimal margin classifiers". Proceedings of the fifth annual workshop on Computational learning theory – COLT '92. p. 144. Chilès, J. P. , Aug, C. , Guillen, A. , Lees, T. (2004), Modelling of geometry of geological units and its uncertainty in 3 D from structural data: the potential-field method, Orebody Modelling and Strategic Mine Planning — Uncertainty and Risk Management Models, Spectrum Series, 14, Australasian Institute of Mining and Metallurgy, Carlton, Victoria, pp. 329– 336. Lajaunie, C. , Courrioux, G. , Manuel, L. (1997) Foliation fields and 3 D cartography in geology: principles of a method based on potential interpolation, Mathematical Geology, 29(4): 571 -584. Mariz, C. , Wagner, L. , Pilger, G. , Whitehouse, P. , Bessin, C. , Laurent, D. (2016), Geostatistical Clustering, Potential Modeling and traditional geostatistics: a new coherent workflow, Minin 2016, 6 th International Conference on Innovation in Mine Operations, pp. 146 -148. Renard, D. , Wagner, L. , Chilès, J. P. , Deraisme, J. , Jahoda, R. Vann, J. (2013) Modelling the geometry of mineral deposit domain with a potential field, 36 th APCOM – Application of Computers and Operations Research in the Mineral Industry, Fundação Luiz Englert, pp. 145 -155. Romary, T. , Ors, F. , Rivoirard, J. , Deraisme, J. (2015) Unsupervised classification of multivariate geostatistical data: two algorithms, Computers and Geosciences, Elsevier 2015, Statistical learning in geoscience modelling: Novel algorithms and challenging case studies, 85, pp. 96 -103. Romary, T. Rivoirard, J. , Deraisme, J. , Quinones, C. , Freulon, X. (2012) Domaining by clustering multivariate geostatistical data, Springer Netherlands, In Geostatistics Oslo 2012, pp. 455 -466.

THANK YOU FOR YOUR ATTENTION…QUESTIONS? More information: mariz@geovariances. com wagner@geovariances. com