DATA ARRANGEMENT AND PRESENTATION formation of tables and

DATA ARRANGEMENT AND PRESENTATION formation of tables and charts

Presentation of data Principles: �Data should be arranged in such a way that it will arouse interest in reader. �The data should be made sufficiently concise without losing important details. �The data should presented in simple form to enable the reader to form quick impressions and to draw some conclusion, directly or indirectly. �Should facilitate further statistical analysis. �It should define the problem and suggest its solution

Methods of presentation of data �The first step in statistical analysis is to present data in an easy way to be understood. �There are three ways for data presentation. These are: ü Textual Method ü Tabulation ü Graphical Method
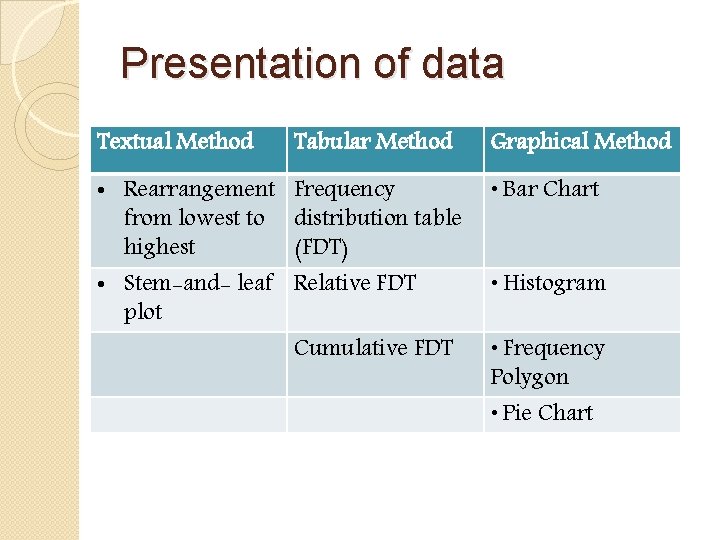
Presentation of data Textual Method Tabular Method Graphical Method • Rearrangement from lowest to highest • Stem-and- leaf plot Frequency distribution table (FDT) • Bar Chart Relative FDT • Histogram Cumulative FDT • Frequency Polygon • Pie Chart
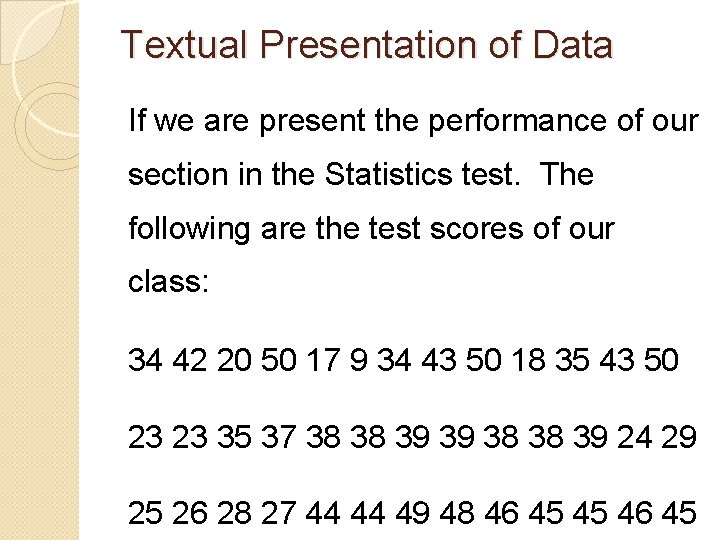
Textual Presentation of Data If we are present the performance of our section in the Statistics test. The following are the test scores of our class: 34 42 20 50 17 9 34 43 50 18 35 43 50 23 23 35 37 38 38 39 39 38 38 39 24 29 25 26 28 27 44 44 49 48 46 45 45 46 45

Solution: First, arrange the data in order for you to identify the important characteristics. This can be done in two ways: rearranging from lowest to highest or using the stem-andleaf plot. Below is the rearrangement of data from lowest to highest: 9 23 28 35 38 43 45 48 17 24 29 37 39 43 45 49 18 25 34 38 39 44 46 50 20 26 34 38 39 44 46 50 23 27 35 38 42 45 46 50

Stem-and-leaf Plot �Data rearrangement is done by making use of the stem-and-leaf plot. �Stem-and-leaf Plot is a table which sorts data according to a certain pattern. It involves separating a number into two parts. In a twodigit number, the stem consists of the first digit, and the leaf consists of the second digit. While in a three-digit number, the stem consists of the first two digits, and the leaf consists of the last digit. In a one-digit number, the stem is zero.

� Below is the stem-and-leaf plot of the ungrouped data given in the example. Stem Leaves 0 9 1 7, 8 2 0, 3, 3, 4, 5, 6, 7, 8, 9 3 4, 4, 5, 5, 7, 8, 8, 9, 9, 9 4 5 2, 3, 3, 4, 4, 5, 5, 5, 6, 6, 6, 8, 9 0, 0, 0 � Utilizing the stem-and-leaf plot, we can readily see the order of the data. Thus, we can say that the top ten got scores 50, 50, 49, 48, 46, 46, 45, and 45 and the ten lowest scores are 9, 17, 18, 20, 23, 24, 25, 26, and 27.

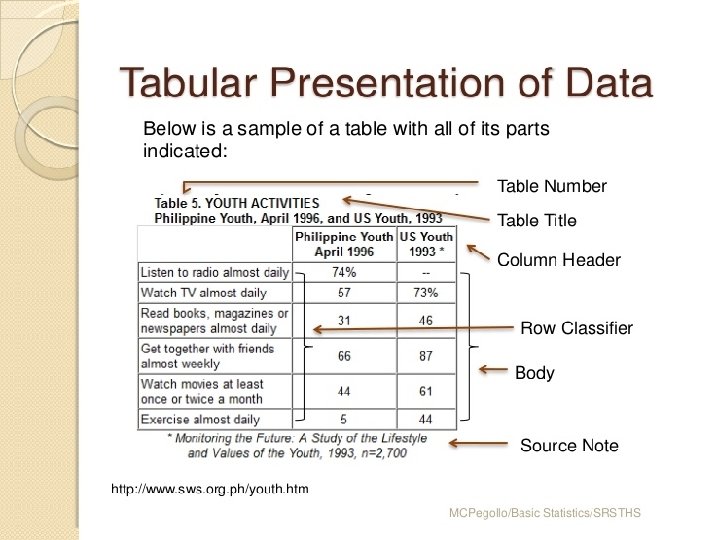
TABULAR METHOD

Rules and guidelines for tabular presentation �Table must be numbered �Brief and self explanatory title must be given to each table. �The heading of columns and rows must be clear, sufficient, concise and fully defined. �The data must be presented according to size of importance, chronologically, alphabetically or geographically �Table should not be too large. �Figures needing comparison should be placed as close as possible

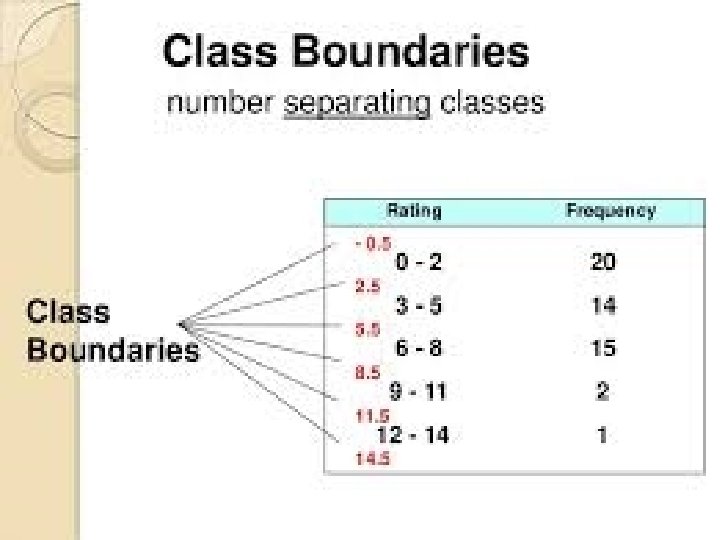
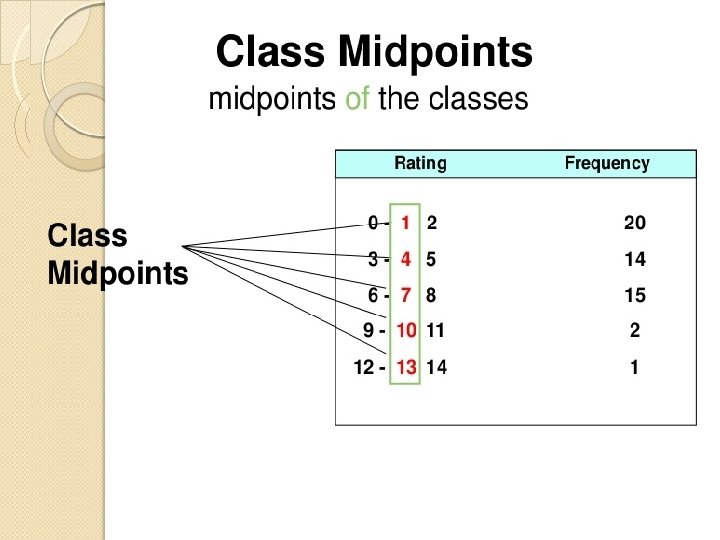
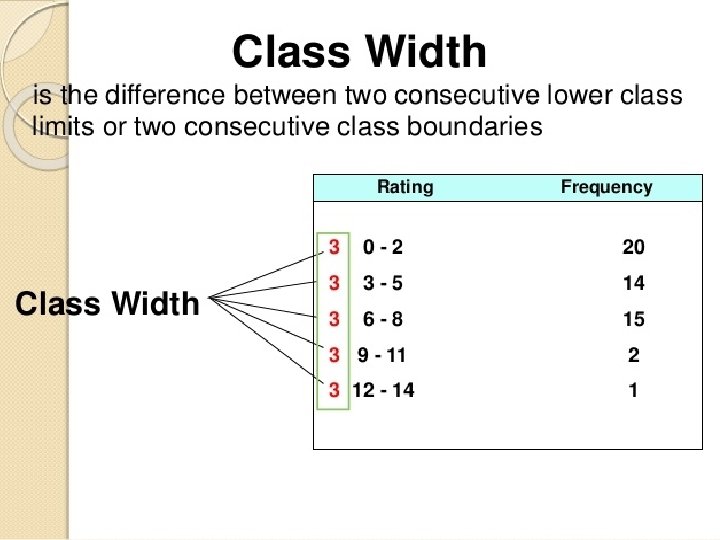
�The classes should be fully defined, should not lead to any ambiguity. �The classes should be exhaustive i. e. should include all the given values. �The classes should be mutually exclusive and non overlapping. �The classes should be of equal width or class interval should be same �Open ended classes should be avoided as far as possible. �The number of classes should be neither too large nor too small. Can be 10 -20 classes. Formula for number of classes(C): C=1+3. 322 log(n), where n is total number of observation in data.
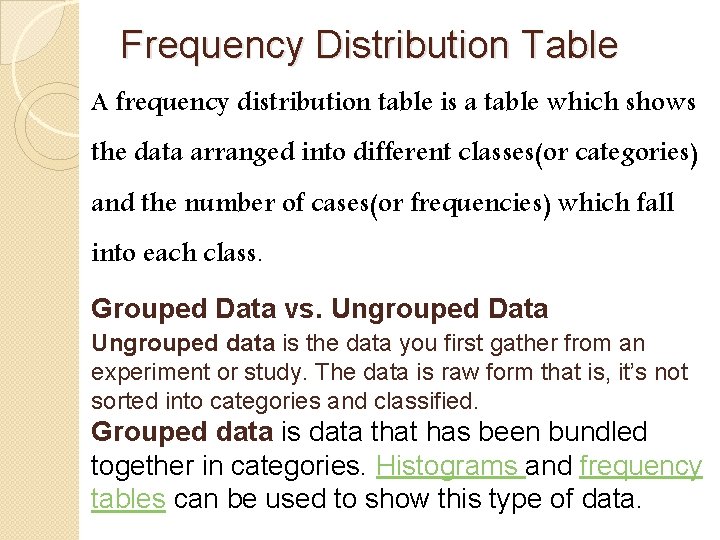
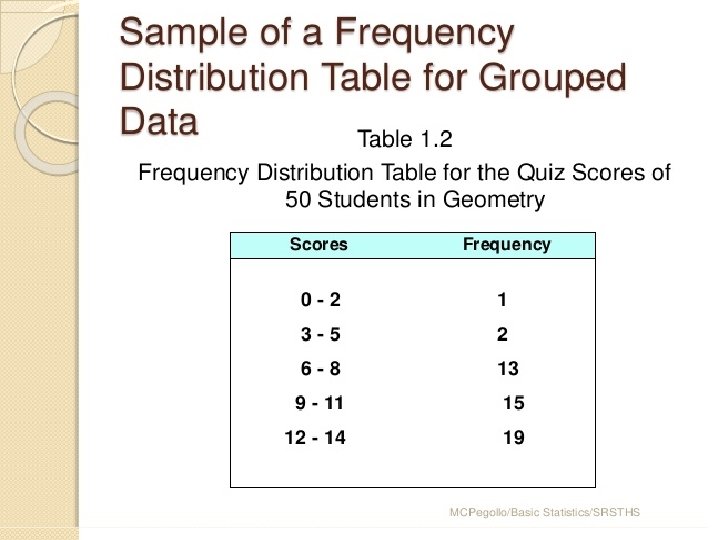
Frequency Distribution Table A frequency distribution table is a table which shows the data arranged into different classes(or categories) and the number of cases(or frequencies) which fall into each class. Grouped Data vs. Ungrouped Data Ungrouped data is the data you first gather from an experiment or study. The data is raw form that is, it’s not sorted into categories and classified. Grouped data is data that has been bundled together in categories. Histograms and frequency tables can be used to show this type of data.

Sample of a Frequency Distribution Table for Ungrouped Data



Relative Frequency Table Relative frequency = class frequency (ƒ) sum of all frequencies(∑ƒ)
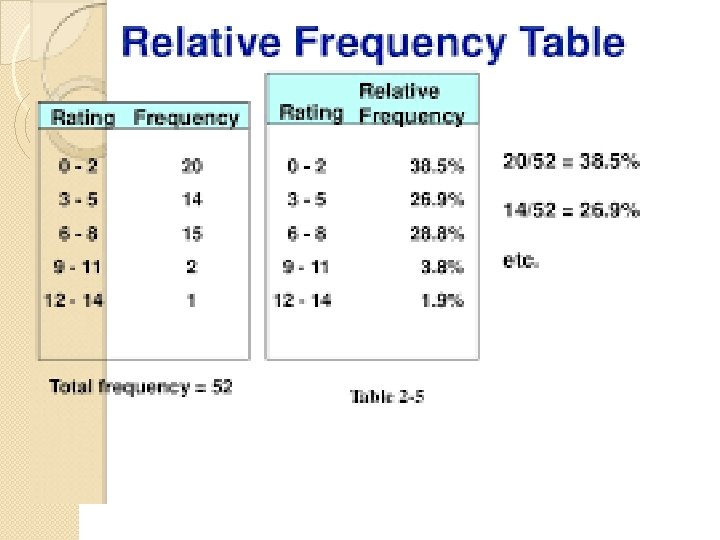
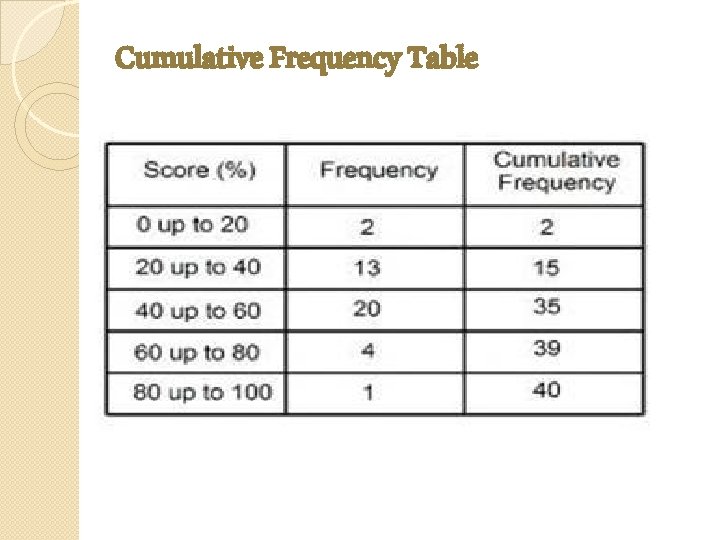
Cumulative Frequency Table
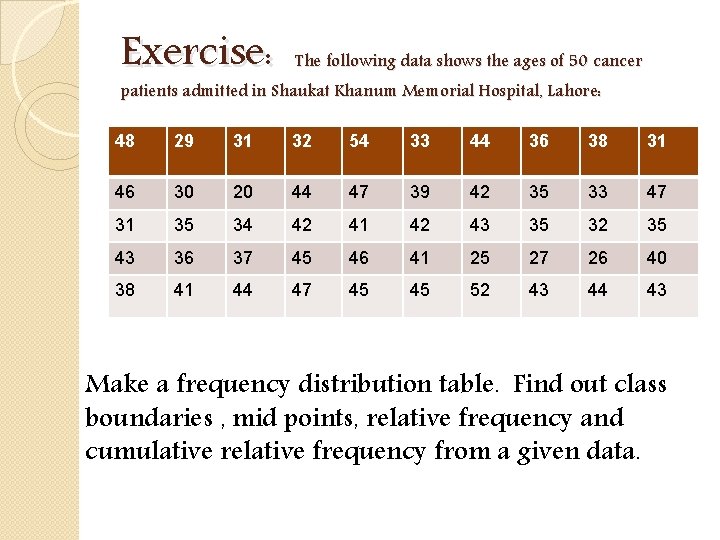
Exercise: The following data shows the ages of 50 cancer 48 29 31 32 54 33 44 36 38 31 46 30 20 44 47 39 42 35 33 47 31 35 34 42 41 42 43 35 32 35 43 36 37 45 46 41 25 27 26 40 38 41 44 47 45 45 52 43 44 43 patients admitted in Shaukat Khanum Memorial Hospital, Lahore: Make a frequency distribution table. Find out class boundaries , mid points, relative frequency and cumulative relative frequency from a given data.

GRAPHICAL METHOD

Charts and diagrams Graphic presentations used to illustrate and clarify information. Tables are essential in presentation of scientific data and diagrams are complementary to summarize these tables in an easy, attractive and simple way.

The Charts should be: • Simple • Easy to understand • Save a lot of words • Self explanatory • Has a clear title indicating its content • Fully labeled • The y axis (vertical) is usually used for frequency

Various charts and diagrams ü Bar Chart ü Histogram ü Frequency polygon ü Cumulative frequency curve ü Scatter Chart ü Line Chart ü Pie diagram

Bar Chart � Widely used, easy to prepare tool for comparing categories of mutually exclusive discrete data. � Different categories are indicated on one axis and frequency of data in each category on another axis. � Length of the bar indicate the magnitude of the frequency of the character to be compared. � The width of the bar and the gaps between the bars should be equal throughout. � The bars may be vertical or horizontal. � 3 types of bar diagram: o Simple o Multiple or compound o Component or proportional
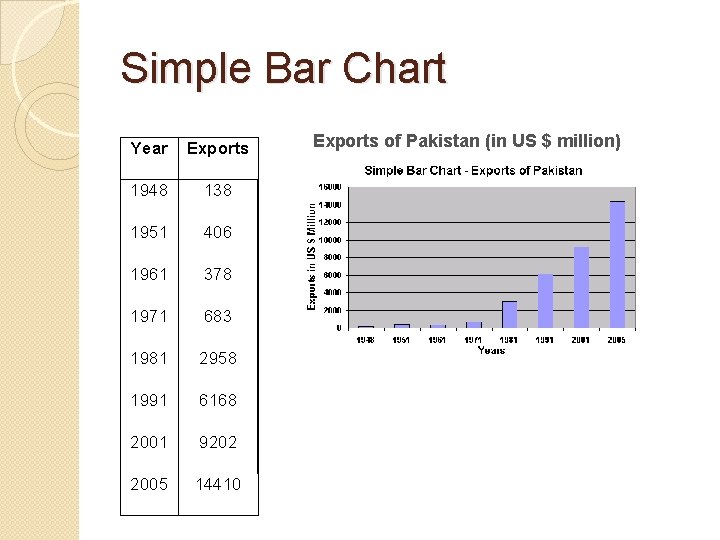
Simple Bar Chart Year Exports 1948 138 1951 406 1961 378 1971 683 1981 2958 1991 6168 2001 9202 2005 14410 Exports of Pakistan (in US $ million)
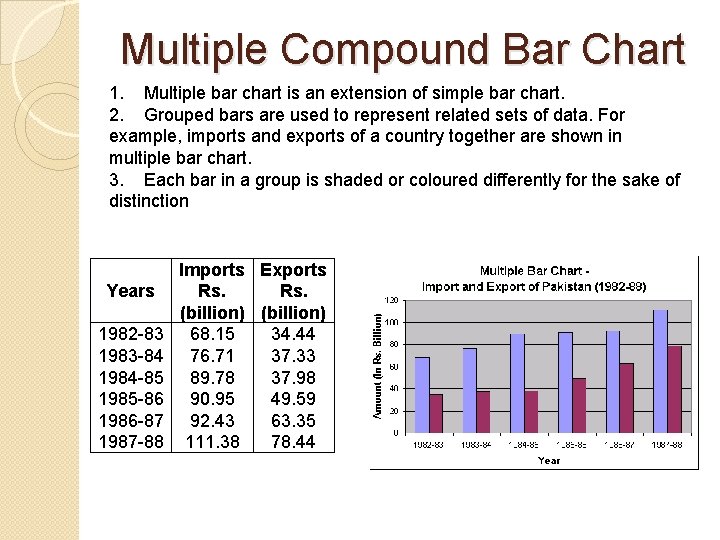
Multiple Compound Bar Chart 1. Multiple bar chart is an extension of simple bar chart. 2. Grouped bars are used to represent related sets of data. For example, imports and exports of a country together are shown in multiple bar chart. 3. Each bar in a group is shaded or coloured differently for the sake of distinction Years 1982 -83 1983 -84 1984 -85 1985 -86 1986 -87 1987 -88 Imports Exports Rs. (billion) 68. 15 34. 44 76. 71 37. 33 89. 78 37. 98 90. 95 49. 59 92. 43 63. 35 111. 38 78. 44

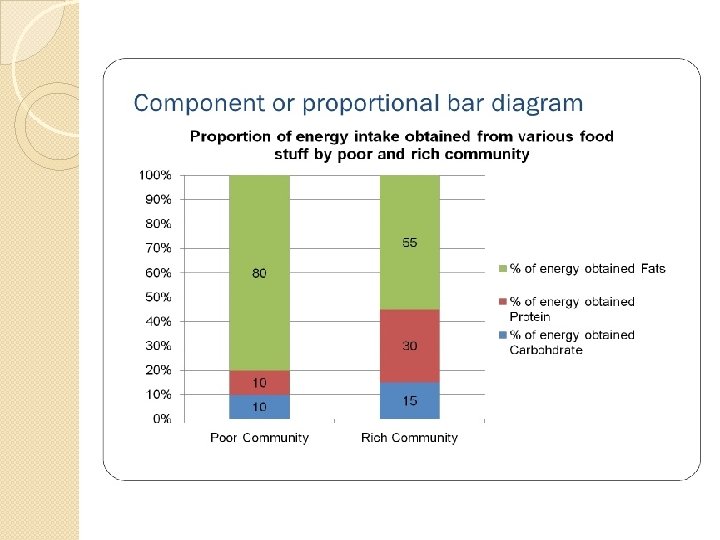
Component or proportional bar chart �Subdivision of a single bar to indicate the composition of the total divided into sections according to their relative proportion. �For example two communities are compared in their proportion of energy obtained from various food stuff, each bar represents energy intake by one community, the height of the bar is 100, it is divided horizontally into 3 components (Protein, Fat and carbohydrate) of diet, each component is represented by different color or shape.

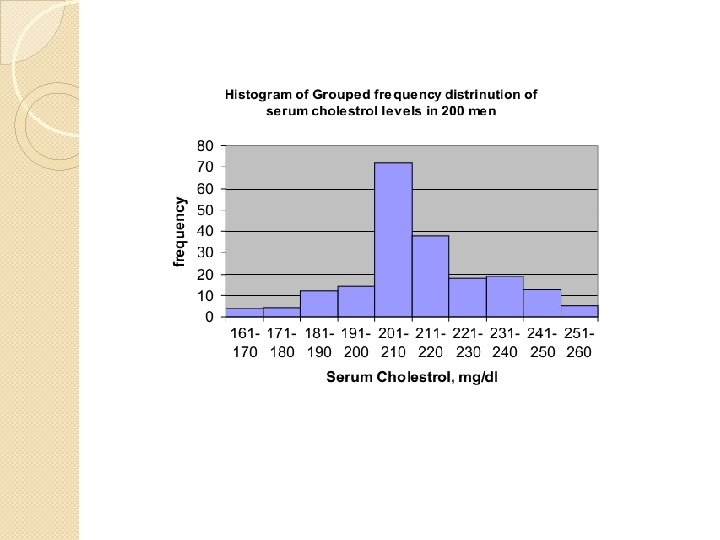
Histogram Used for Quantitative, Continuous Variables. § It is used to present variables which have no gaps e. g age, weight, height, blood pressure, blood sugar etc. § It consist of a series of blocks. The class intervals are given along horizontal axis and the frequency along the vertical axis. §

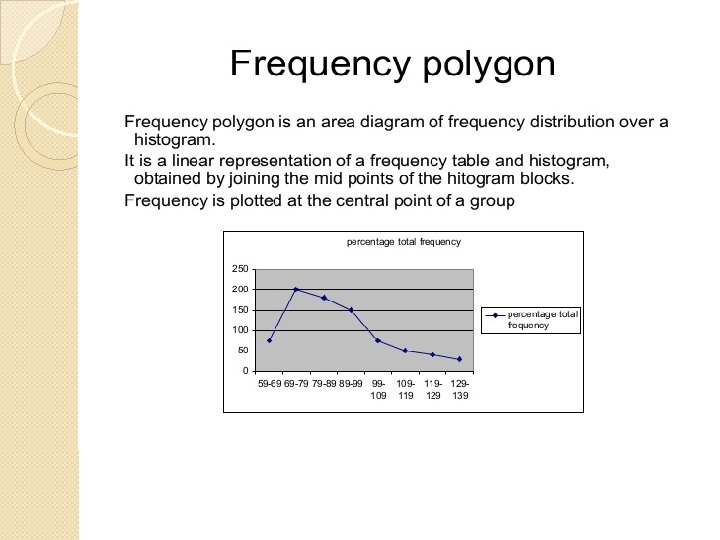
Frequency Polygon �Derived from a histogram by connecting the mid points of the tops of the rectangles in the histogram. �The line connecting the centers of histogram rectangles is called frequency polygon. �We can draw polygon without rectangles so we will get simpler form of line graph. �A special type of frequency polygon is the Normal Distribution Curve.
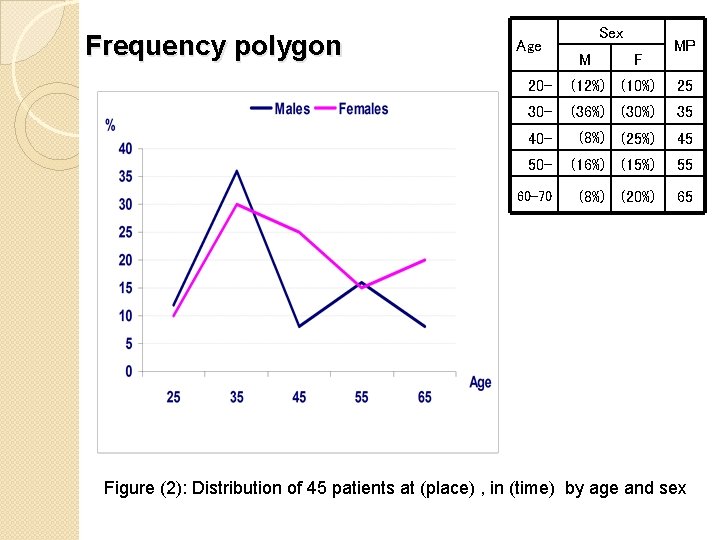
Frequency polygon Age Sex MP M F 20 - (12%) (10%) 25 30 - (36%) (30%) 35 40 - (8%) (25%) 45 50 - (16%) (15%) 55 60 -70 (8%) (20%) 65 Figure (2): Distribution of 45 patients at (place) , in (time) by age and sex
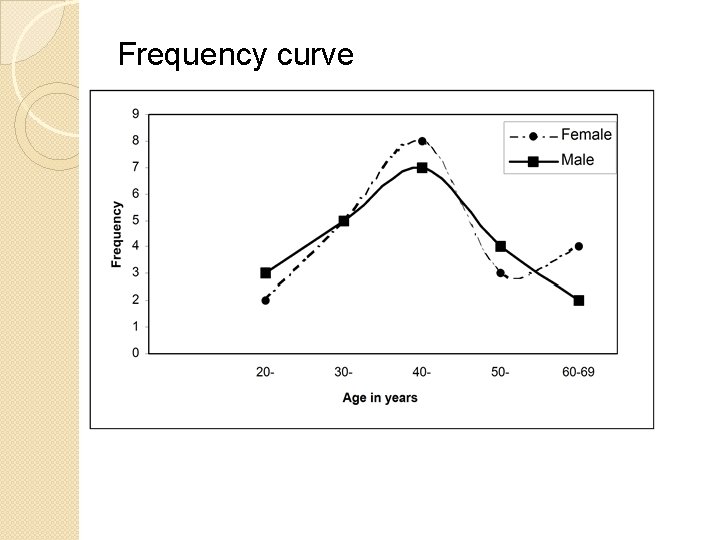
Frequency curve

Cumulative frequency diagram or O’give � An ogive is a graph that represents cumulative frequencies or cumulative relative frequencies of a data set. � The cumulative frequency is plotted on the y-axis against the data which is on the x-axis for un-grouped data. When dealing with grouped data, the Ogive is formed by plotting the cumulative frequency against the upper boundary of the class.
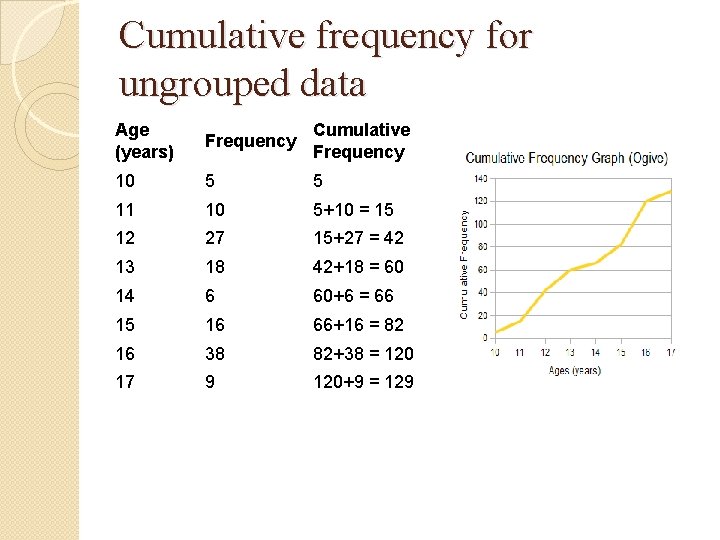
Cumulative frequency for ungrouped data Age (years) Frequency Cumulative Frequency 10 5 5 11 10 5+10 = 15 12 27 15+27 = 42 13 18 42+18 = 60 14 6 60+6 = 66 15 16 66+16 = 82 16 38 82+38 = 120 17 9 120+9 = 129
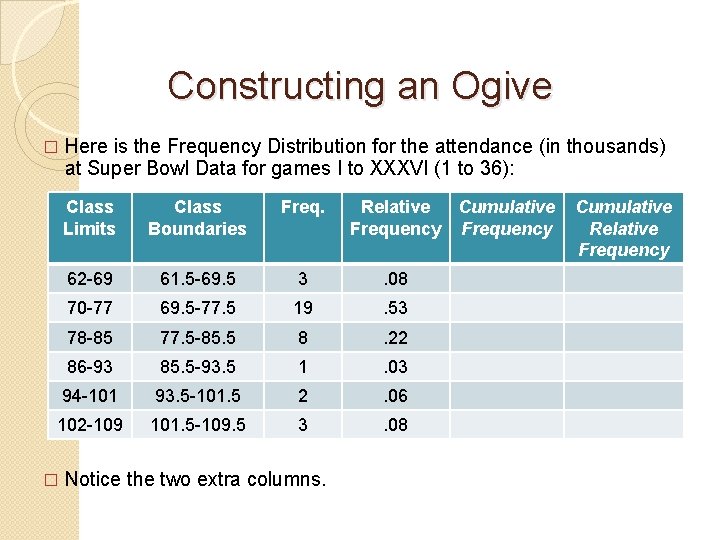
Constructing an Ogive � Here is the Frequency Distribution for the attendance (in thousands) at Super Bowl Data for games I to XXXVI (1 to 36): Class Limits Class Boundaries Freq. 62 -69 61. 5 -69. 5 3 . 08 70 -77 69. 5 -77. 5 19 . 53 78 -85 77. 5 -85. 5 8 . 22 86 -93 85. 5 -93. 5 1 . 03 94 -101 93. 5 -101. 5 2 . 06 102 -109 101. 5 -109. 5 3 . 08 � Notice the two extra columns. Relative Cumulative Frequency Cumulative Relative Frequency
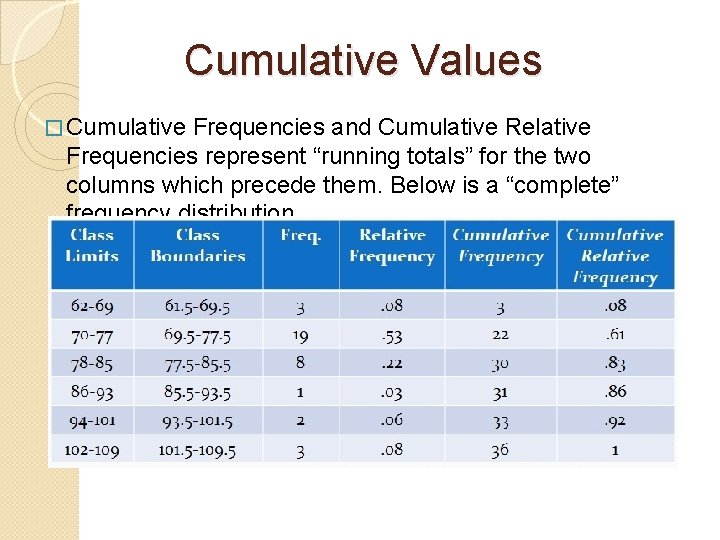
Cumulative Values � Cumulative Frequencies and Cumulative Relative Frequencies represent “running totals” for the two columns which precede them. Below is a “complete” frequency distribution.
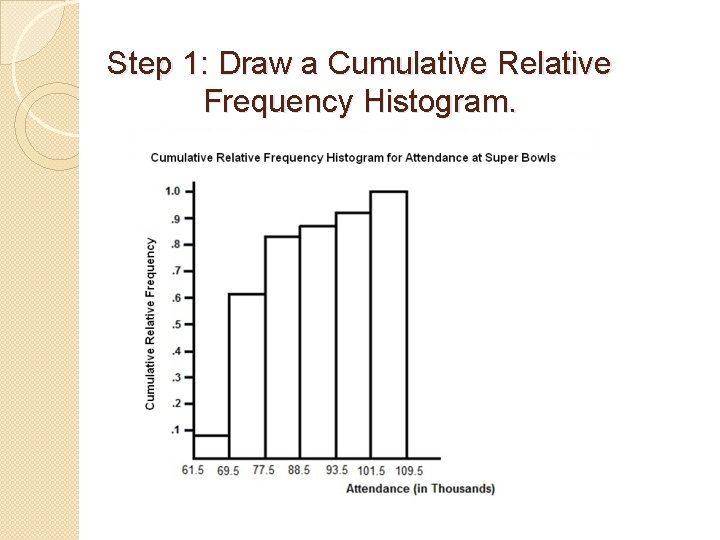
Step 1: Draw a Cumulative Relative Frequency Histogram.
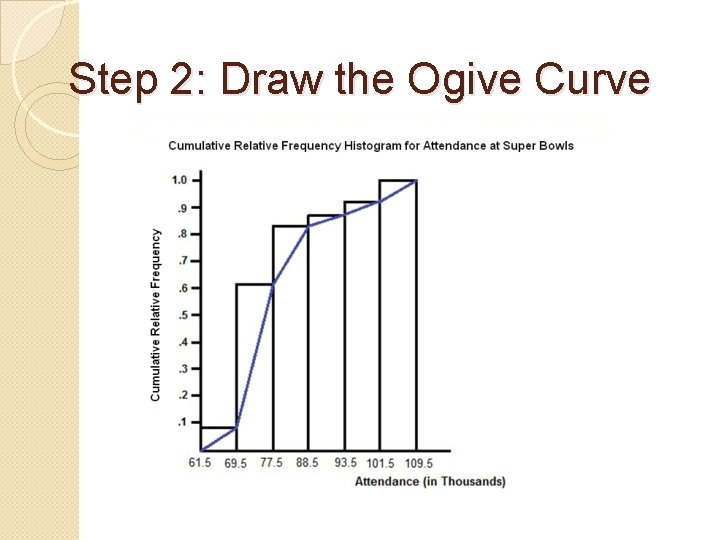
Step 2: Draw the Ogive Curve
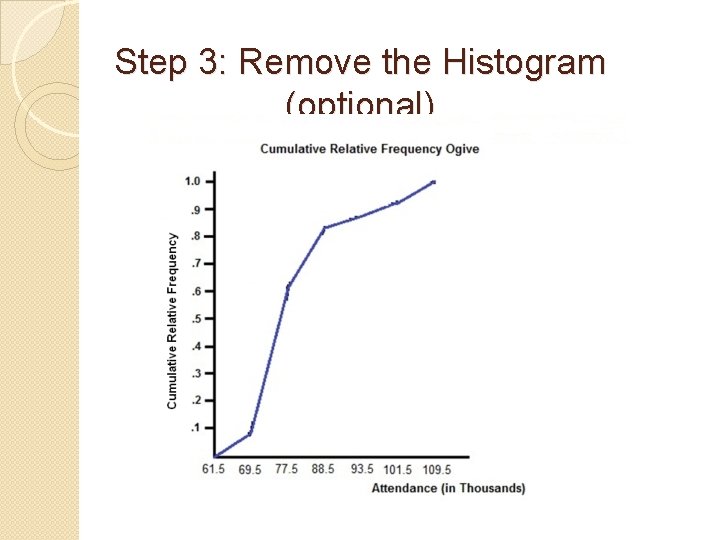
Step 3: Remove the Histogram (optional)

Percentiles A percentile is a certain percentage of a set of data. Percentiles are used to observe how many of a given set of data fall within a certain percentage range; for example; a thirtieth percentile indicates data that lies the 13% mark of the entire data set. Calculating Percentiles Percentile as Pm where m represents the percentile we're finding, for example for the tenth percentile, m} would be 10. Given that the total number of elements in the data set is N

Quartiles The term quartile is derived from the word quarter which means one fourth of something. Thus a quartile is a certain fourth of a data set. When you arrange a date set increasing order from the lowest to the highest, then you divide this data into groups of four, you end up with quartiles. There are three quartiles that are studied in statistics. � First Quartile (Q 1)-------(1⁄4) 25 th percentile (n + 1) ÷ 4 � Second Quartile (Q 2) ---(2⁄4) 50 th percentile 2(n + 1) ÷ 4 � Third Quartile (Q 3)------(3⁄4) 75 th percentile 3(n + 1) ÷ 4
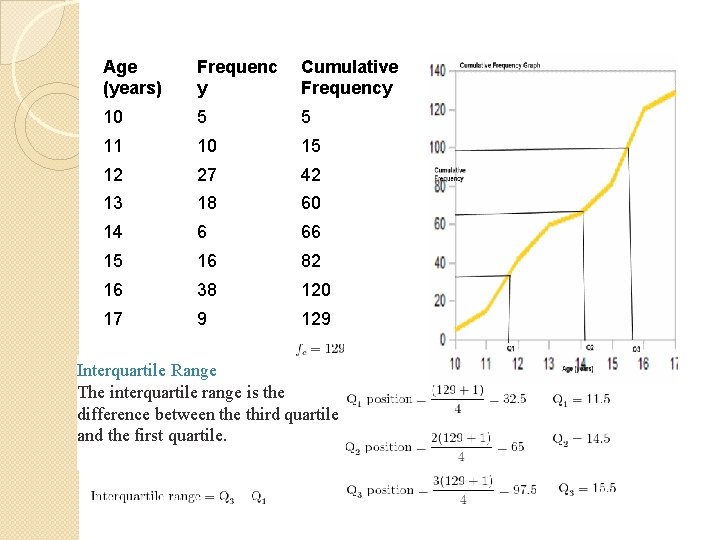
Age (years) Frequenc y Cumulative Frequency 10 5 5 11 10 15 12 27 42 13 18 60 14 6 66 15 16 82 16 38 120 17 9 129 Interquartile Range The interquartile range is the difference between the third quartile and the first quartile.

Scatter/ dot diagram �Also called as Correlation diagram , it is useful to represent the relationship between two numeric measurements, each observation being represented by a point corresponding to its value on each axis. �In negative correlation, the points will be scattered in downward direction, meaning that the relation between the two studied measurements is controversial i. e. if one measure increases the other decreases �While in positive correlation, the points will be scattered in upward direction.
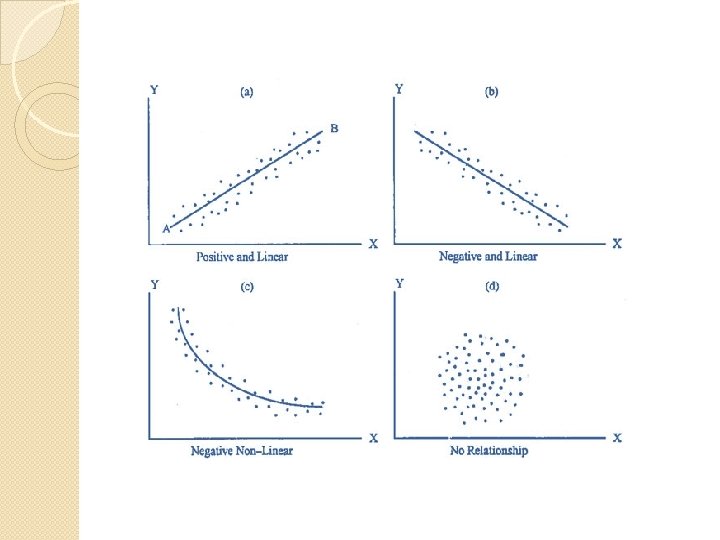

Line diagram: �It is diagram showing the relationship between two numeric variables (as the scatter) but the points are joined together to form a line. �Used to show the trend of events with the passage of time


Pie diagram: Consist of a circle whose area represents the total frequency (100%) which is divided into segments. Each segment represents a proportional composition of the total frequency. A pie chart is a circular statistical graphic which is divided into slices to illustrate numerical proportion. In a pie chart, the arc length of each slice is proportional to the quantity it represents. The formula to determine the angle of a sector in a circle graph is: Q = Component Part x 360˚ Total
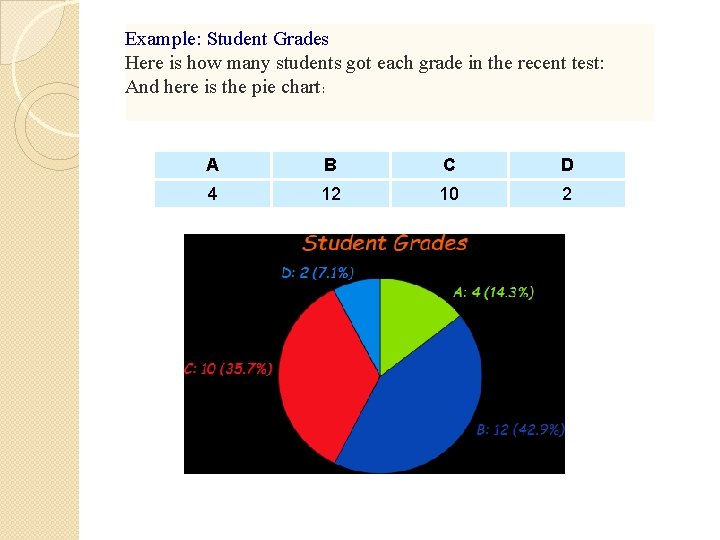
Example: Student Grades Here is how many students got each grade in the recent test: And here is the pie chart: A B C D 4 12 10 2
- Slides: 55