Data analysis using regression modeling visual display and

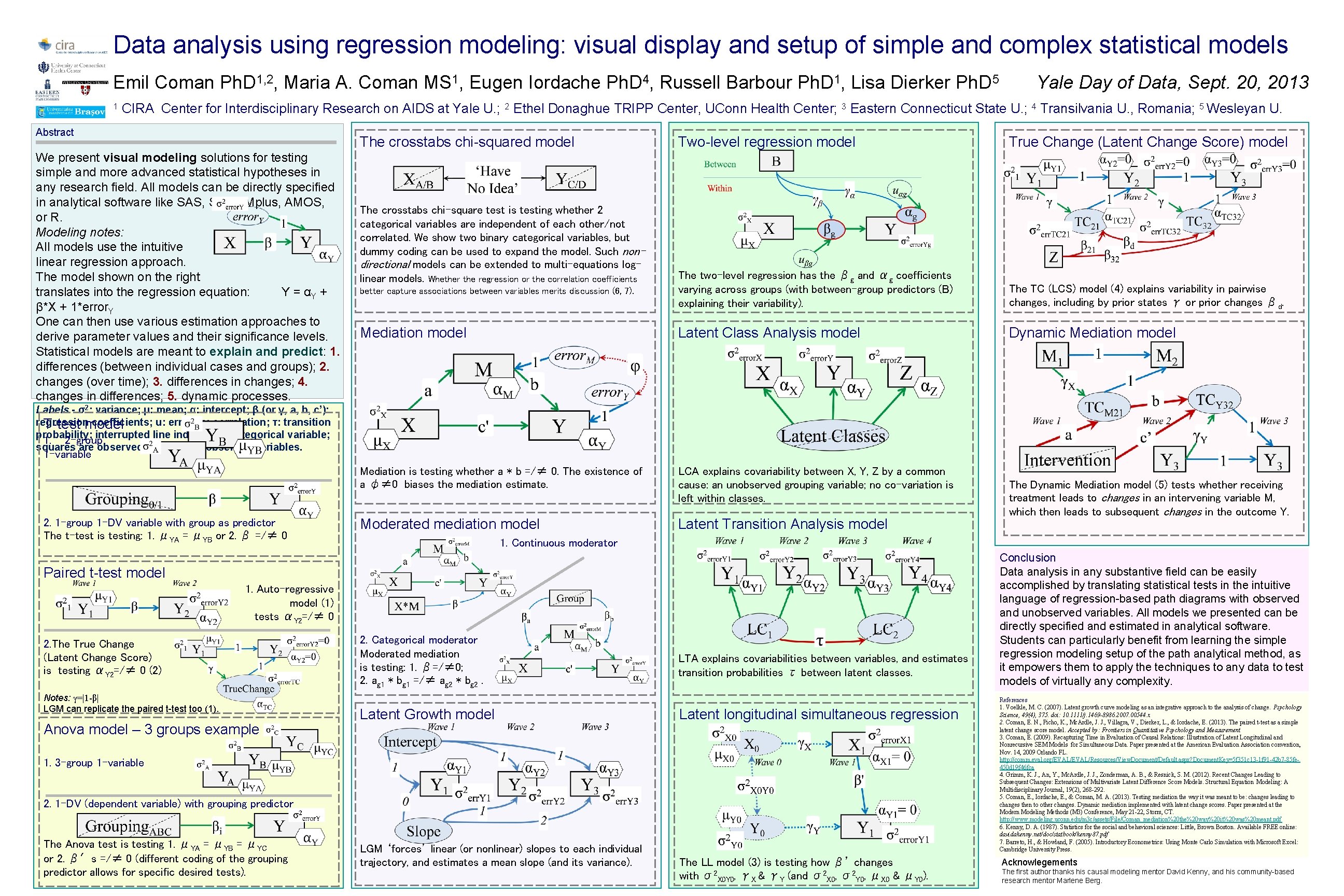
Data analysis using regression modeling: visual display and setup of simple and complex statistical models Emil Coman Ph. D 1, 2, Maria A. Coman MS 1, Eugen Iordache Ph. D 4, Russell Barbour Ph. D 1, Lisa Dierker Ph. D 5 1 Yale Day of Data, Sept. 20, 2013 CIRA Center for Interdisciplinary Research on AIDS at Yale U. ; 2 Ethel Donaghue TRIPP Center, UConn Health Center; 3 Eastern Connecticut State U. ; 4 Transilvania U. , Romania; 5 Wesleyan U. Abstract The crosstabs chi-squared model We present visual modeling solutions for testing simple and more advanced statistical hypotheses in any research field. All models can be directly specified in analytical software like SAS, Stata, Mplus, AMOS, or R. Modeling notes: All models use the intuitive linear regression approach. The model shown on the right translates into the regression equation: Y = αY + β*X + 1*error. Y One can then use various estimation approaches to derive parameter values and their significance levels. Statistical models are meant to explain and predict: 1. differences (between individual cases and groups); 2. changes (over time); 3. differences in changes; 4. changes in differences; 5. dynamic processes. Two-level regression model True Change (Latent Change Score) model better capture associations between variables merits discussion (6, 7). The two-level regression has the βg and αg coefficients varying across groups (with between-group predictors (B) explaining their variability). The TC (LCS) model (4) explains variability in pairwise changes, including by prior states γ or prior changes βd. Mediation model Latent Class Analysis model Dynamic Mediation model Mediation is testing whether a * b =/≠ 0. The existence of a φ≠ 0 biases the mediation estimate. LCA explains covariability between X, Y, Z by a common cause: an unobserved grouping variable; no co-variation is left within classes. Moderated mediation model Latent Transition Analysis model The crosstabs chi-square test is testing whether 2 categorical variables are independent of each other/not correlated. We show two binary categorical variables, but dummy coding can be used to expand the model. Such nondirectional models can be extended to multi-equations loglinear models. Whether the regression or the correlation coefficients Labels - σ2: variance; μ: mean; α: intercept; β (or γ, a, b, c’): regression coefficients; u: error; φ: correlation; τ: transition T-test model probability; interrupted line indicates a categorical variable; 1. 2 -group squares are observed, ellipses un-observed variables. 1 -variable 2. 1 -group 1 -DV variable with group as predictor The t-test is testing: 1. μYA = μYB or 2. β =/≠ 0 1. Continuous moderator Paired t-test model 1. Auto-regressive model (1) tests αY 2=/≠ 0 2. The True Change (Latent Change Score) is testing αY 2=/≠ 0 (2) Notes: γ=|1 -β| LGM can replicate the paired t-test too (1). Anova model – 3 groups example 2. Categorical moderator Moderated mediation is testing: 1. β=/≠ 0; 2. ag 1 * bg 1 =/≠ ag 2 * bg 2. Latent Growth model LTA explains covariabilities between variables, and estimates transition probabilities τ between latent classes. Latent longitudinal simultaneous regression 1. 3 -group 1 -variable 2. 1 -DV (dependent variable) with grouping predictor The Anova test is testing 1. μYA = μYB = μYC or 2. β′s =/≠ 0 (different coding of the grouping predictor allows for specific desired tests). The Dynamic Mediation model (5) tests whether receiving treatment leads to changes in an intervening variable M, which then leads to subsequent changes in the outcome Y. LGM ‘forces’ linear (or nonlinear) slopes to each individual trajectory, and estimates a mean slope (and its variance). The LL model (3) is testing how β’ changes with σ2 X 0 Y 0, γX & γY (and σ2 X 0, σ2 Y 0, μX 0 & μY 0). Conclusion Data analysis in any substantive field can be easily accomplished by translating statistical tests in the intuitive language of regression-based path diagrams with observed and unobserved variables. All models we presented can be directly specified and estimated in analytical software. Students can particularly benefit from learning the simple regression modeling setup of the path analytical method, as it empowers them to apply the techniques to any data to test models of virtually any complexity. References 1. Voelkle, M. C. (2007). Latent growth curve modeling as an integrative approach to the analysis of change. Psychology Science, 49(4), 375. doi: 10. 1111/j. 1469 -8986. 2007. 00544. x 2. Coman, E. N. , Picho, K. , Mc. Ardle, J. J. , Villagra, V. , Dierker, L. , & Iordache, E. (2013). The paired t-test as a simple latent change score model. Accepted by: Frontiers in Quantitative Psychology and Measurement 3. Coman, E. (2009). Recapturing Time in Evaluation of Causal Relations: Illustration of Latent Longitudinal and Nonrecursive SEM Models for Simultaneous Data. Paper presented at the American Evaluation Association convention, Nov. 14, 2009 Orlando FL. http: //comm. eval. org/EVAL/Resources/View. Document/Default. aspx? Document. Key=5 f 351 c 13 -1 f 91 -42 b 7 -85 fe 450 d 19 f 46 fca 4. Grimm, K. J. , An, Y. , Mc. Ardle, J. J. , Zonderman, A. B. , & Resnick, S. M. (2012). Recent Changes Leading to Subsequent Changes: Extensions of Multivariate Latent Difference Score Models. Structural Equation Modeling: A Multidisciplinary Journal, 19(2), 268 -292. 5. Coman, E. , Iordache, E. , & Coman, M. A. (2013). Testing mediation the way it was meant to be: changes leading to changes then to other changes. Dynamic mediation implemented with latent change scores. Paper presented at the Modern Modeling Methods (M 3) Conference, May 21 -22, Storrs, CT. http: //www. modeling. uconn. edu/m 3 c/assets/File/Coman_mediation%20 the%20 way%20 it%20 was%20 meant. pdf 6. Kenny, D. A. (1987). Statistics for the social and behavioral sciences: Little, Brown Boston. Available FREE online: davidakenny. net/doc/statbook/kenny 87. pdf 7. Barreto, H. , & Howland, F. (2005). Introductory Econometrics: Using Monte Carlo Simulation with Microsoft Excel: Cambridge University Press. Acknowlegements The first author thanks his causal modeling mentor David Kenny, and his community-based research mentor Marlene Berg.