DATA ANALYSIS Module Code CA 660 Application Areas

DATA ANALYSIS Module Code : CA 660 (Application Areas: Bio-, Business, Environment etc. )

STRUCTURE of Investigation/DA 1, 2, many samples Replication, E. D. , Regn. , C. T. Assays, Counts Estimation/H. T. Study techniques Lab. techniques Non-Parametric Distributional Assumptions, Probability , Estimation properties Basis: Size/Type of Data Set/Tools Level of Measurement 2

Probability & Statistics Primer -overview Note: Short overview. Other statistical distributions in lectures 3

Summary Statistics- Descriptive When analysing practical sets of data, it is useful to be able to define a small number of values that summarise the main features present. We will derive (i) representative values, (ii) measures of spread and (iii) measures of skewness and other characteristics. Representative Values These are sometimes called measures of location or measures of central tendency. 1. Random Value Given a set of data S = { x 1, x 2, … , xn }, we select a random number, say k, in the range 1 to n and return the value xk. This method of generating a representative value is straightforward, but it suffers from the fact that extreme values can occur and successive values could vary considerably from one another. 2. Arithmetic Mean For the set S above, the arithmetic mean (or just mean) is x = {x 1 + x 2 + … + xn }/ n. If x 1 occurs f 1 times, x 2 occurs f 2 times and so on, we get the formula x = { f 1 x 1 + f 2 x 2 + … + f n xn } / { f 1 + f 2 + … + f n } , written x = fx / f 4

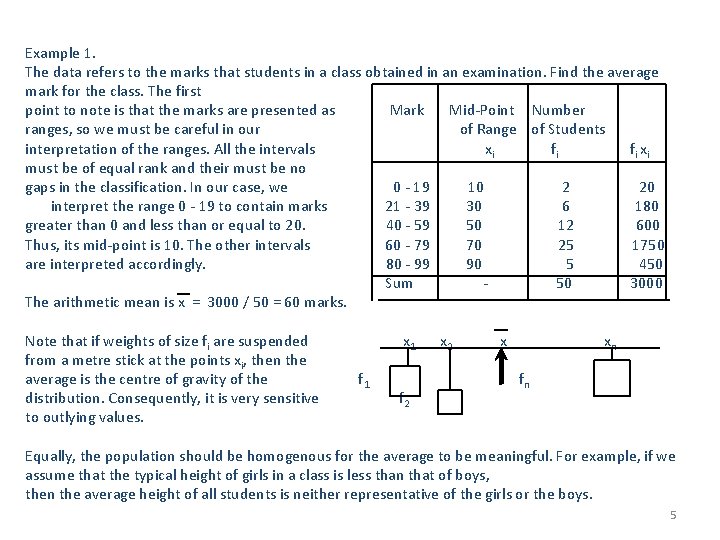
Example 1. The data refers to the marks that students in a class obtained in an examination. Find the average mark for the class. The first point to note is that the marks are presented as Mark Mid-Point Number ranges, so we must be careful in our of Range of Students interpretation of the ranges. All the intervals xi fi f i xi must be of equal rank and their must be no gaps in the classification. In our case, we 0 - 19 10 2 20 interpret the range 0 - 19 to contain marks 21 - 39 30 6 180 greater than 0 and less than or equal to 20. 40 - 59 50 12 600 Thus, its mid-point is 10. The other intervals 60 - 79 70 25 1750 are interpreted accordingly. 80 - 99 90 5 450 Sum 50 3000 The arithmetic mean is x = 3000 / 50 = 60 marks. Note that if weights of size fi are suspended from a metre stick at the points xi, then the average is the centre of gravity of the distribution. Consequently, it is very sensitive to outlying values. x 1 f 2 x xn fn Equally, the population should be homogenous for the average to be meaningful. For example, if we assume that the typical height of girls in a class is less than that of boys, then the average height of all students is neither representative of the girls or the boys. 5

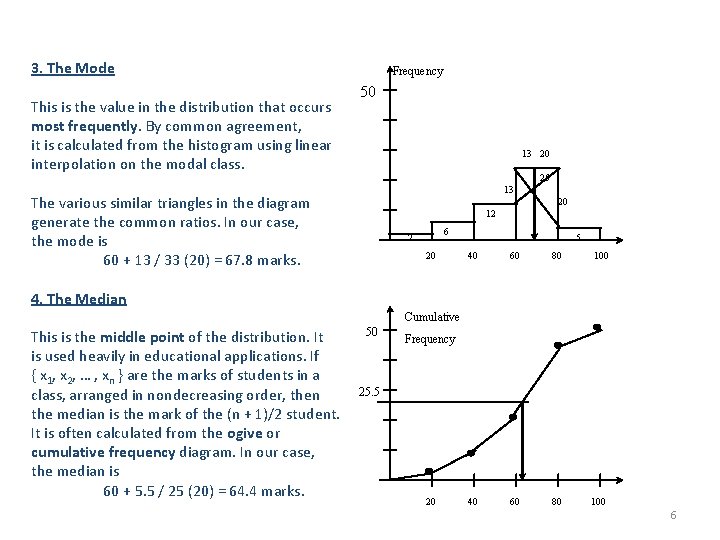
3. The Mode This is the value in the distribution that occurs most frequently. By common agreement, it is calculated from the histogram using linear interpolation on the modal class. Frequency 50 13 20 25 13 The various similar triangles in the diagram generate the common ratios. In our case, the mode is 60 + 13 / 33 (20) = 67. 8 marks. 20 12 6 2 20 5 40 60 80 100 4. The Median Cumulative This is the middle point of the distribution. It is used heavily in educational applications. If { x 1, x 2, … , xn } are the marks of students in a class, arranged in nondecreasing order, then the median is the mark of the (n + 1)/2 student. It is often calculated from the ogive or cumulative frequency diagram. In our case, the median is 60 + 5. 5 / 25 (20) = 64. 4 marks. 50 Frequency 25. 5 20 6

Measures of Dispersion or Scattering Example 2. The following distribution has the same arithmetic mean as example 1, but the values are more dispersed. This illustrates the point that an average value on its own may not be adequately describe statistical distributions. To devise a formula that traps the degree to which a distribution is concentrated about the average, we consider the deviations of the values from the average. If the distribution is concentrated around the mean, then the deviations will be small, while if the distribution is very scattered, then the deviations will be large. The average of the squares of the deviations is called the variance and this is used as a measure of dispersion. The square root of the variance is called the standard deviation and has the same units of measurement as the original values and is the preferred measure of dispersion in many applications. Marks x Frequency f fx 10 30 50 70 90 Sums 6 8 6 15 15 50 60 240 300 1050 1350 3000 x 6 x 5 x 4 x 3 x 2 x 1 x 7

Variance & Standard Deviation 2 = VAR[X] = Average of the Squared Deviations = S f { Squared Deviations } / S f = S f { xi - x } 2 / S f = S f xi 2 / S f - x 2 , called the product moment formula. = Standard Deviation = Variance Example 1 f 2 6 12 25 5 50 x 10 30 50 70 90 fx 20 180 600 1750 450 3000 VAR [X] = 198600 / 50 - (60) 2 = 372 marks 2 f x 2 200 5400 30000 122500 40500 198600 Example 2 f 6 8 6 15 15 50 x 10 30 50 70 90 fx 60 240 300 1050 1350 3000 f x 2 600 7200 15000 73500 121500 217800 VAR [X] = 217800 / 50 - (60)2 = 756 marks 2 8

Other Summary Statistics Skewness An important attribute of a statistical distribution relates to its degree of symmetry. The word “skew” means a tail, so that distributions that have a large tail of outlying values on the right-handside are called positively skewed or skewed to the right. The notion of negative skewness is defined similarly. A simple formula for skewness is Skewness = ( Mean - Mode ) / Standard Deviation which in the case of example 1 is: Skewness = (60 - 67. 8) / 19. 287 = - 0. 4044. Coefficient of Variation This formula was devised to standardise the arithmetic mean so that comparisons can be drawn between different distributions. . However, it has not won universal acceptance. Coefficient of Variation = Mean / standard Deviation. Semi-Interquartile Range Just as the median corresponds to the 0. 50 point in a distribution, the quartiles Q 1, Q 2, Q 3 correspond to the 0. 25, 0. 50 and 0. 75 points. An alternative measure of dispersion is Semi-Interquartile Range = ( Q 3 - Q 1 ) / 2. Geometric Mean For data that is growing geometrically, such as economic data with a high inflation effect, an alternative to the arithmetic mean is preferred. It involves getting the root to the power N = S f of a product of terms Geometric Mean = N x 1 f 1 x 2 f 2 … xk fk 9

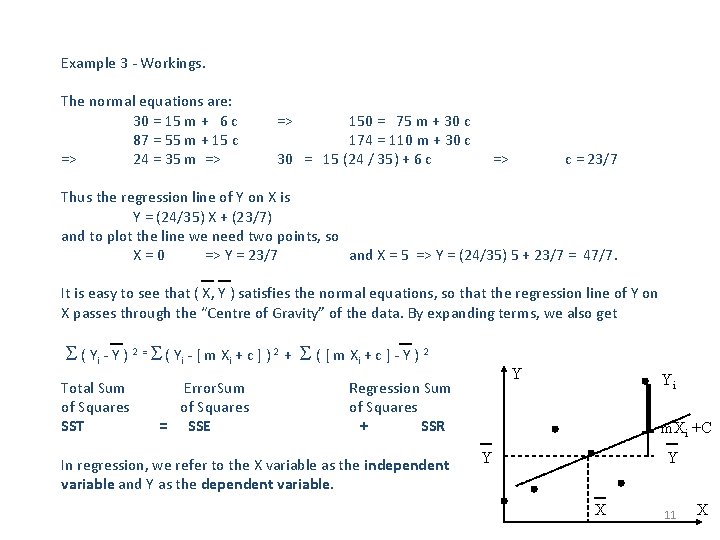
Regression [Example 3. ] As a motivating example, suppose we are modelling sales data over time. SALES 3 5 4 5 6 7 TIME 1990 1991 1992 1993 1994 1995 Y=m. X+c We seek the straight line “Y = m X + c” that best Y Yi approximates the data. By “best” in this case, we mean the line which minimizes the sum of squares of vertical deviations of points from the line: m Xi + c SS = S ( Yi - [ m. Xi + c ] ) 2. Setting the partial derivatives of SS with respect to m and c to zero leads to the “normal equations” 0 X S Y = m S X + n. c , where n = # points S X. Y= m S X 2 + c S X. Xi Let 1990 correspond to Year 0. X. X 0 1 4 9 16 25 X 0 1 2 3 4 5 X. Y 0 5 8 15 24 35 Y 3 5 4 5 6 7 Y. Y 9 25 16 25 36 49 55 15 87 30 160 Sales 10 5 Time 0 5 10

Example 3 - Workings. The normal equations are: 30 = 15 m + 6 c 87 = 55 m + 15 c => 24 = 35 m => => 150 = 75 m + 30 c 174 = 110 m + 30 c 30 = 15 (24 / 35) + 6 c => c = 23/7 Thus the regression line of Y on X is Y = (24/35) X + (23/7) and to plot the line we need two points, so X=0 => Y = 23/7 and X = 5 => Y = (24/35) 5 + 23/7 = 47/7. It is easy to see that ( X, Y ) satisfies the normal equations, so that the regression line of Y on X passes through the “Centre of Gravity” of the data. By expanding terms, we also get S ( Yi - Y ) 2 = S ( Yi - [ m X i + c ] ) 2 Total Sum of Squares SST Error. Sum of Squares = SSE + S ( [ m Xi + c ] - Y ) 2 Y Regression Sum of Squares + SSR In regression, we refer to the X variable as the independent variable and Y as the dependent variable. Yi m. Xi +C Y Y X 11 X

Correlation The coefficient of determination r 2 ( which takes values in the range 0 to 1) is a measure of the proportion of the total variation that is associated with the regression process: r 2 = SSR/ SST = 1 - SSE / SST. The coefficient of correlation r ( which takes values in the range -1 to +1 ) is more commonly used as a measure of the degree to which a mathematical relationship exists between X and Y. (Dashed lines show association). It can be calculated from the formula: r = (X-X)(Y-Y) = ( X - X )2 ( Y - Y ) 2 n XY- X Y [{ n X 2 - ( X ) 2 } { n Y 2 - ( Y ) 2 }] Example. In our case r = {6(87) - (15)(30)}/ { 6(55) - (15)2 } { 6 (160) - (30)2 } = 0. 907. r=-1 r=0 r=+1 12

Collinearity If the value of the correlation coefficient is greater than 0. 9 or less than - 0. 9, we would take this to mean that there is a mathematical relationship between the variables. This does not imply that a cause-and-effect relationship exists. Consider a country with a slowly changing population size, where a certain political party retains a relatively stable per centage of the poll in elections. Let X = Number of people that vote for the party in an election Y = Number of people that die due to a given disease in a year Z = Population size. Then, the correlation coefficient between X and Y is likely to be close to 1, indicating that there is a mathematical relationship between them (i. e. ) X is a function of Z and Y is a function of Z also. It would clearly be silly to suggest that the incidence of the disease is caused by the number of people that vote for the given political party. This is known as the problem of collinearity. Spotting hidden dependencies between distributions can be difficult. Statistical experimentation can only be used to disprove hypotheses, or to lend evidence to support the view that reputed relationships between variables may be valid. Thus, the fact that we observe a high correlation coefficient between deaths due to heart failure in a given year with the number of cigarettes consumed twenty years earlier does not establish a causeand-effect relationship. However, this result may be of value in directing biological research. 13

Overview of Probability Theory In statistical theory, an experiment is any operation that can be replicated infinitely often and gives rise to a set of elementary outcomes, which are deemed to be equally likely. The sample space S of the experiment is the set of all possible outcomes of the experiment. Any subset E of the sample space is called an event. We say that an event E occurs whenever any of its elements is an outcome of the experiment. The probability of occurrence of E is P {E} = Number of elementary outcomes in E Number of elementary outcomes in S S E The complement E of an event E is the set of all elements that belong to S but not to E. The union of two events E 1 E 2 is the set of all outcomes that belong to E 1 or to E 2 or to both. The intersection of two events E 1 E 2 is the set of all events that belong to both E 1 and E 2. Two events are mutually exclusive if the occurrence of either precludes the occurrence of the other (i. e) their intersection is the empty set. Two events are independent if the occurrence of either is unaffected by the occurrence or non-occurrence of the other event. Theorem of Total Probability. P {E 1 E 2} = P{E 1} + P{E 2} - P{E 1 E 2} Proof. P{E 1 E 2} = (n 1, 0 + n 1, 2 + n 0, 2) / n = (n 1, 0 + n 1, 2) / n + (n 1, 2 + n 0, 2) / n - n 1, 2 / n = P{E 1} + P{E 2} - P{E 1 E 2} S n = n 0, 0 + n 1, 0 + n 0, 2 + n 1, 2 E 1 n 1, 0 E 2 n 1, 2 n 0, 2 Corollary. If E 1 and E 2 are mutually exclusive, P{E 1 E 2} = P{E 1} + P{E 2} - see Axioms and Addition Rule n 0, 0 14

The probability P{E 1 | E 2} that E 1 occurs, given that E 2 has occurred (or must occur) is called the conditional probability of E 1. Note that in this case, the only possible outcomes of the experiment are S confined to E 2 and not to S. E 2 E 1 Theorem of Compound Probability Multiplication Rule. n 1, 0 n 1, 2 P{E 1 E 2} = P{E 1 | E 2} * P{E 2}. n 0, 2 Proof. P{E 1 E 2} = n 1, 2 / n n 0, 0 = {n 1, 2 / (n 1, 2 + n 0, 2) } * { n 1, 2 + n 0, 2) / n} Corollary If E 1 and E 2 are independent, P{E 1 E 2} = P{E 1} * P{E 2}. Special case of Multiplication Rule Note: If an E itself compound, expands further = Chain Rule: P{E 7 E 8 E 9} =P{E 7 (E 8 E 9)} Ability to count possible outcomes in an event is crucial to calculating probs. By a permutation of size r of n different items, we mean an arrangement of r of the items, where the order of the arrangement is important. If the order is not important, the arrangement is called a combination. Example. There are 5*4 permutations and 5*4 / (2*1) combinations of size 2 of A, B, C, D, E Permutations: AB, BA, AC, CA, AD, DA, AE, EA CD, DC, CE, EC BC, CB, BD, DB, BE, EB DE, ED Combinations: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE Standard reference books on probability theory give a comprehensive treatment of how these ideas are used to calculate the probability of occurrence of the outcomes of games of chance. 15

Bayes’ Rule (Theorem): For a series of mutually exclusive and exhaustive events Br, where union of the Br = B 1 B 2 B 3 ……. Br = all possibilities for B, Then: Where denominator is the Total probability of A occurring. Ex. Paternity indices: based on actual genotypes of mother, child, and alleged father. Before collection of any evidence, have a prior probability of paternity P{C}. So, what is the situation after the genetic evidence ‘E’ is in? From Bayes’: P {man is father | E} P{man not father | E} = P[E | man is father} P{E | man not father} P{man is father} P{man not father} Written in terms of ratio of posterior probs. (= LHS), paternity index (L say) and ratio of prior probs. (RHS). Rearrange and substitute in above to give prob. of an alleged man with particular genotype ‘C’ being the true father NB: L is a way of ‘weighting’ the genetic evidence; the issue is setting a prior. 16

Statistical Distributions- Characterisation If a statistical experiment only gives rise to real numbers, the outcome of the experiment is called a random variable. If a random variable X takes values X 1 , X 2 , … , X n with probabilities p 1 , p 2 , … , p n the expected (average) value of X is defined to be E[X] = p j Xj and its variance is VAR[X] = E[X 2] - E[X]2 = pj Xj 2 - E[X]2. Example. Let X be a random variable measuring the distance in Kilometres travelled by children to a school and suppose that the following data applies. Then the mean and variance are E[X] = 5. 30 Kilometres VAR[X] = 33. 80 - 5. 302 = 5. 71 Kilometres 2 Prob. pj Distance Xj pj Xj 2 0. 15 2. 0 0. 30 0. 60 0. 40 4. 0 1. 60 6. 40 0. 20 6. 0 1. 20 7. 20 0. 15 8. 0 1. 20 9. 60 0. 10 10. 0 1. 00 5. 30 33. 80 Similar concepts apply to continuous distributions. The distribution function is defined by F(t) = P{ X t} and its derivative is the frequency function f(t) = d F(t) / dt so that F(t) = f(x) dx. 17

Sums and Differences of Random Variables Define the covariance of two random variables to be COVAR [ X, Y] = E [(X - E[X]) (Y - E[Y]) ] = E[X Y] - E[X] E[Y]. If X and Y are independent, COVAR [X, Y] = 0. Lemma E[ X + Y] = E[X] + E[Y] VAR [ X + Y] = VAR [X] + VAR [Y] + 2 COVAR [X, Y] E[ k. X] = k. E[X] VAR[ k. X] = k 2. E[X] for a constant k. Example. A company records the journey time X of a lorry from a depot to customers and the unloading times Y, as shown. E[X] = {1(10)+2(13)+3(17)+4(10)}/50 = 2. 54 2 E[X ] = {12(10+22(13)+32(17)+42(10)}/50 = 7. 5 VAR[X] = 7. 5 - (2. 54)2 = 1. 0484 E[Y] = {1(20)+2(19)+3(11)}/50 = 1. 82 VAR[Y] = 3. 9 - (1. 82)2 = 0. 5876 X= Y =1 2 3 Totals 1 7 2 1 10 2 5 6 2 13 3 4 8 5 17 4 4 3 3 10 Totals 20 19 11 50 E[Y 2] = {12(20)+22(19)+32(11)}/50 = 3. 9 E[X+Y] = { 2(7)+3(5)+4(4)+5(4)+3(2)+4(6)+5(8)+6(3)+4(1)+5(2)+6(5)+7(3)}/50 = 4. 36 2 E[(X + Y) ] = {22(7)+32(5)+42(4)+52(4)+32(2)+42(6)+52(8)+62(3)+42(1)+52(2)+62(5)+72(3)}/50 = 21. 04 VAR[(X+Y)] = 21. 04 - (4. 36)2 = 2. 0304 E[X Y] = {1(7)+2(5)+3(4)+4(4)+2(2)+4(6)+6(8)+8(3)+3(1)+6(2)+9(5)+12(3)}/50 = 4. 82 COVAR (X, Y) = 4. 82 - (2. 54)(1. 82) = 0. 1972 VAR[X] + VAR[Y] + 2 COVAR[ X, Y] = 1. 0484 + 0. 5876 + 2 ( 0. 1972) = 2. 0304 18

Standard Statistical Distributions Most elementary statistical books provide a survey of commonly used statistical distributions. Importantly, we can characterise them by their expectation and variance (as for random variables) and by the parameters on which these are based; (see lecture notes for those we will refer to). So, e. g. for a Binomial distribution, the parameters are p the probability of success in an individual trial and n the No. of trials. The probability of success remains constant – otherwise, another distribution applies. Use of the correct distribution is core to statistical inference – I. e. estimating what is happening in the population on the basis of a (correctly drawn, probabilistic) sample. The sample is then representative of the population. Fundamental to statistical inference is the Normal (or Gaussian), with parameters, the mean (or more formally expectation of the distribution) and (or 2), the Standard deviation ( Variance). For small samples, or when 2 not known but must be estimated from the sample, a slightly more conservative distribution applies = the Student’s T or just ‘t’ distribution. Introduces the degrees of freedom concept. 19

Student’s t Distribution A random variable X has a t distribution with n degrees of freedom ( tn ). The t distribution is symmetrical about the origin, with E[X] =0 VAR [X] = n / (n -2). For small values of n, the tn distribution is very flat. As n is increased the density assumes a bell shape. For values of n ³ 25, the tn distribution is practically indistinguishable from the standard normal curve. O If X and Y are independent random variables If X has a standard normal distribution and Y has a cn 2 distribution then X has a tn distribution (Y / n) O If x 1, x 2, … , xn is a random sample from a normal distribution, with mean and variance 2 and if we define s 2 = 1 / ( n - 1) ( xi - x ) 2 then ( x - ) / ( s / n) has a tn- 1 distribution Estimated Sample variance - se 3 e calculators. , tables etc. + Many other standard distributions 20

Sampling Theory The procedure for drawing a random sample a distribution is that numbers 1, 2, … are assigned to the elements of the distribution and tables of random numbers are then used to decide which elements are included in the sample. If the same element can not be selected more than once, we say that the sample is drawn without replacement; otherwise, the sample is said to be drawn with replacement. The usual convention in sampling is that lower case letters are used to designate the sample characteristics, with capital letters being used for the parent population. Thus if the sample size is n, its elements are designated, x 1, x 2, …, xn, its mean is x and its modified variance is s 2 = (xi - x )2 / (n - 1). The corresponding parent population characteristics are N (or infinity), X and S 2. Suppose that we repeatedly draw random samples of size n (with replacement) from a distribution with mean and variance 2. Let x 1, x 2, … be the collection of sample means and let xi ’ = xi - (i = 1, 2, … ) / n The collection x 1’, x 2’, … is called the sampling distribution of means, (usual U or Z) Central Limit Theorem. In the limit, as sample size n tends to infinity, the sampling distribution of means has a standard normal distribution. Basis for statistical inference. 21

Attribute and Proportionate Sampling If the sample elements area measurement of some characteristic, we are said to have attribute sampling. On the other hand if all the sample elements are 1 or 0 (success/failure, agree/ no-not-agree), we have proportionate sampling. For proportionate sampling, the sample average x and the sample proportion p are synonymous, just as are the mean and proportion P for the parent population. From our results on the Binomial distribution, the sample variance is p (1 - p) and the variance of the parent distribution is P (1 - P). We can generalise the concept of the sampling distribution of means to get the sampling distribution of any statistic. We say that a sample characteristic is an unbiased estimator of the parent population characteristic, i. e. the expectation of the corresponding sampling distribution is equal to the parent characteristic. Lemma. The sample average (proportion ) is an unbiased estimator of the parent average (proportion): E [ x] = ; so E [p] = P. The quantity ( N - n) / ( N - 1) is called the finite population correction (fpc). If the parent population is infinite or we have sampling with replacement the fpc = 1. Lemma. E [s] = S * fpc for estimated sample S. D. with fpc 22

Confidence Intervals From the statistical tables for a Standard Normal (Gaussian) distribution, we note that Area Under Density Function 0. 90 0. 95 0. 99 From To -1. 64 -1. 96 -2. 58 1. 64 1. 96 2. 58 n (0, 1) 0. 95 -1. 96 0 +1. 96 From the central limit theorem, if x and s 2 are the mean and variance of a random sample of size n (with n greater than 25) drawn from a large parent population, then we can make the following statement about the unknown parent mean Prob { -1. 64 £ x - £ 1. 64) » 0. 90 s/ n i. e. Prob { x - 1. 64 s / n £ £ x + 1. 64 s / n } » 0. 90 The range x + 1. 64 s / n is called a 90% confidence interval for the parent mean . Example [ Attribute Sampling] A random sample of size 25 has x = 15 and s = 2. Then a 95% confidence interval for is 15 + 1. 96 (2 / 5) (i. e. ) 14. 22 to 15. 78 Example [ Proportionate Sampling] A random sample of size n = 1000 has p = 0. 40 Þ 1. 96 p (1 - p) / (n - 1) = 0. 03. A 95% confidence interval for P is 0. 40 + 0. 03 (i. e. ) 0. 37 to 0. 43. 23

Small Sampling Theory For reference purposes, it is useful to regard the expression x + 1. 96 s / n as the “default formula” for a confidence interval and to modify it to suit particular circumstances. O If we are dealing with proportionate sampling, the sample proportion is the sample mean and the standard error (s. e. ) term s / n simplifies as follows: x -> p and s / n -> p(1 - p) / (n -1). (Also n-1 -> n) O A 90% confidence interval will bring about the swap 1. 96 -> 1. 64. O If the sample size n is less than 25, the normal distribution must be replaced by Student’s t n - 1 distribution. O For sampling without replacement from a finite population, a fpc term must be used. The width of the confidence interval band increases with the confidence level. Example. A random sample of size n = 10, drawn from a large parent population, has a mean x = 12 and a standard deviation s = 2. Then a 99% confidence interval for the parent mean is x + 3. 25 s / n (i. e. ) 12 + 3. 25 (2)/3 (i. e. ) 9. 83 to 14. 17 and a 95% confidence interval for the parent mean is x + 2. 262 s / n (i. e. ) 12 + 2. 262 (2)/3 (i. e. ) 10. 492 to 13. 508. Note that for n = 1000, 1. 96 p (1 - p) / n » 0. 03 for values of p between 0. 3 and 0. 7. This gives rise to the statement that public opinion polls have an “inherent error of 3%”. This simplifies calculations in the case of public opinion polls for large political parties. 24

Tests of Hypothesis [Motivational Example]. It is claimed that the average grade of all 12 year old children in a country in a particular aptitude test is 60%. A random sample of n= 49 students gives a mean x = 55% with a standard deviation s = 2%. Is the sample finding consistent with the claim? We regard the original claim as a null hypothises (H 0) which is tentatively accepted as TRUE: Z(0, 1) H 0 : = 60. If the null hypothesis is true, the test statistic Z(0, 1) 0. 95 t= x- s/ n -1. 96 is a Random Variable with a Normal (0, 1) = Standardised Normal Z(0, 1) (or U(0, 1)distribution. Thus 55 - 60 = - 35 / 2 = - 17. 5 2/ 49 rejection regions is a random value from Z(0, 1). But this lies outside the 95% confidence interval (falls in the rejection region), so either (i) The null hypothesis is incorrect or (ii) An event with a probability of at most 0. 05 has occurred. Consequently, we reject the null hypothesis, knowing a probability of 0. 05 exists that we are in error. Technically, we say we reject the null hypothesis at the 0. 05 level of significance. The alternative to rejecting H 0, is to declare the test to be inconclusive. This means that there is some tentative evidence to support the view that H 0 is approximately correct. 25

Modifications Based on the properties of the Normal , student t and other distributions, we can generalise these ideas. If the sample size n < 25, we should use a tn-1 distribution; we can also vary the level of significance of the test and we can apply the tests to proportionate sampling environments. Example. 40% of a random sample of 1000 people in a country indicate satisfaction with government policy. Test at the 0. 01 level of significance if this consistent with the claim that 45% of the people support government policy? Here, H 0: P = 0. 45 p = 0. 40, n = 1000 so p (1 -p) / n = 0. 015 test statistic = (0. 40 - 0. 45) / 0. 015 = - 3. 33 99% critical value = 2. 58 so H 0 is rejected at the. 01 level of significance. One-Tailed Tests If the null hypothesis is of the form H 0 : P ³ 0. 45 then arbitrary large values of p are acceptable, so that the rejection region for the test statistic lies in the left hand tail only. Example. 40% of a random sample of 1000 people in a country indicate satisfaction with government policy. Test at the 0. 05 level of significance if this consistent with the claim that at least 45% of the people support government policy? n(0, 1) Here the critical value is -1. 64, so the null hypothesis H 0: P ³ 0. 45 0. 95 is rejected at the. 05 level of significance -1. 64 Rejection region 26

Testing Differences between Means Suppose that x 1 x 2 … xm is a random sample with mean x and standard deviation s 1 drawn from a distribution with mean 1 and y 1 y 2 … y n and standard deviation s 1 y 2 … yn is a random sample with mean y drawn from a distribution with mean 2. Suppose that we wish to test the null hypothesis that both samples are drawn from the same parent population (i. e. ) H 0: 1 = 2. The pooled estimate of the parent variance is * 2 = { (m - 1) s 12 + (n - 1) s 22 } / ( m + n - 2) and the variance of x - y, being the variance of the difference of two independent random variables, is ’ 2 = *2 / m + * 2 / n. This allows us to construct the test statistic, which under H 0 has a tm+n-2 distribution. Example. A random sample of size m = 25 has mean x = 2. 5 and standard deviation s 1 = 2, while a second sample of size n = 41 has mean y = 2. 8 and standard deviation s 2 = 1. Test at the 0. 05 level of significance if the means of the parent populations are identical. Here H 0 : 1 = 2 x - y = - 0. 3 and *2 = {24(4) + 40(1)} / 64 = 2. 125 so the test statistic is - 0. 3 / (2. 125 / 25 + 2. 125 / 41) = - 0. 811 The 0. 05 critical value for Z(0, 1) is 1. 96, so the test is inconclusive. 27

Paired Tests If the sample values ( xi , yi ) are paired, such as the marks of students in two examinations, then let di = xi - yi be their differences and treat these values as the elements of a sample to generate a test statistic for the hypothesis H 0: 1 = 2. The test statistic d / sd / n has a tn-1 distribution if H 0 is true. Example. In a random sample of 100 students in a national examination their examination mark in English is subtracted from their continuous assessment mark, giving a mean of 5 and a standard deviation of 2. Test at the. 01 level of significance if the true mean mark for both components is the same. Here n = 100, d = 5, sd / n = 2/10 = 0. 2 so the test statistic is 5 / 0. 2 = 10. the 0. 01 critical value for a Z(0, 1) distribution is 2. 58, so H 0 is rejected at the. 01 level of significance. Tests for the Variance. For normally distributed random variables, given H 0: 2 = k, a constant, then (n-1) s 2 / k has a c 2 n - 1 distribution. Example. A random sample of size 30 drawn from a normal distribution has variance s 2 = 5. Test at the. 05 level of significance if this is consistent with H 0 : 2 = 2. Test statistic = (29) 5 /2 = 72. 5, while the 0. 05 critical value for c 229 is 45. 72, so H 0 is rejected at the 0. 05 level of significance. 28

Chi-Square Test of Goodness of Fit This can be used to test the hypothesis H 0 that a set of observations is consistent with a given probability distribution. We are given a set of categories and for each we record the observed O j nd expected Ej number of observations that fall in each category. Under H 0, the test statistic S (Oj - Ej )2 / Ej has a c 2 n - 1 distribution, where n is the number of categories. Example. A pseudo random number generator is used to generate 40 random numbers in the range 1 - 100. Test at the 0. 05 level of significance if the results are consistent with the hypothesis that the outcomes are randomly distributed. Range Observed Number Expected Number 1 -25 6 10 26 - 50 12 10 51 - 75 14 10 76 - 100 8 10 Total 40 40 Test statistic = (6 -10)2/10 + (12 -10)2/10 + (14 -10)2/10 + (8 -10)2/10 = 4. The 0. 05 critical value of c 23 = 7. 81, so the test is inconclusive. Chi-Square Contingency Test To test that two random variables are statistically independent, a set of observations can be recorded in a table with m rows corresponding to categories for one random variable and n columns for the other. Under H 0, the expected number of observations for the cell in row i and column j is the appropriate row total by the column total divided by the grand total. Under H 0, 29 the test statistic S (Oij - Eij )2 / Eij has a c 2(m -1)(n-1) distribution.

Chi-Square Contingency Test - Example In the following table, the figures in brackets are the expected values. The test statistic is Results Honours Pass Fail Totals Maths 100 (50) 130 (225) 70 (25) 300 History Geography 70 (67) 30 (83) 320 (300) 450 (375) 10 (33) 20 (42) 400 500 Totals 200 900 1200 S (Oij - Eij )2 / Eij = (100 -50)2/ 50 + (70 - 67)2/ 67 + (30 -83)2/ 83 + (130 -225)2/ 225 + (320 -300)2/ 300 + (450 -375)2/375 + (70 -25)2/ 25 + (10 -33)2/ 33 + (20 -42)2/ 42 = 248. 976 The 0. 05 critical value for c 22 * 2 is 9. 49 so H 0 is rejected at the 0. 05 level of significance. In general the chi square tests tend to be very conservative vis-a-vis other tests of hypothesis, (i. e. ) they tend to give inconclusive results. The meaning of the term “degrees of freedom”. In simplified terms, as the chi-square distribution is the sum of, say k, squares of independent random variables, it is defined in a k-dimensional space. When we impose a constraint of the type that the sum of observed and expected observations in a column are equal or estimate a parameter of the parent distribution, we reduce the dimensionality of the space by 1. In the case of the chi-square contingency table, with m rows and n columns, the expected values in the final row and column are predetermined, so the number of degrees of freedom of the test statistic is (m-1) (n-1). 30

Analysis of Variance/Experimental Design -Many samples, Means and Variances • Analysis of Variance (AOV or ANOVA) was originally devised for agricultural statistics on e. g. crop yields. Typically, row and column format, = small plots of a fixed size. The yield yi, j within each plot was recorded. 1 y 1, 2 y 1, 3 2 y 2, 1 y 2, 2 y 2, 3 3 y 3, 1 y 3, 2 y 3, 3 y 1, 4 y 1, 5 One Way classification Model: where yi, j = + i, j , = overall mean th i = effect of the i factor i, j = error term. Hypothesis: H 0: 1 = 2 =… = i , j ~ N (0, 2) in the limit m 31

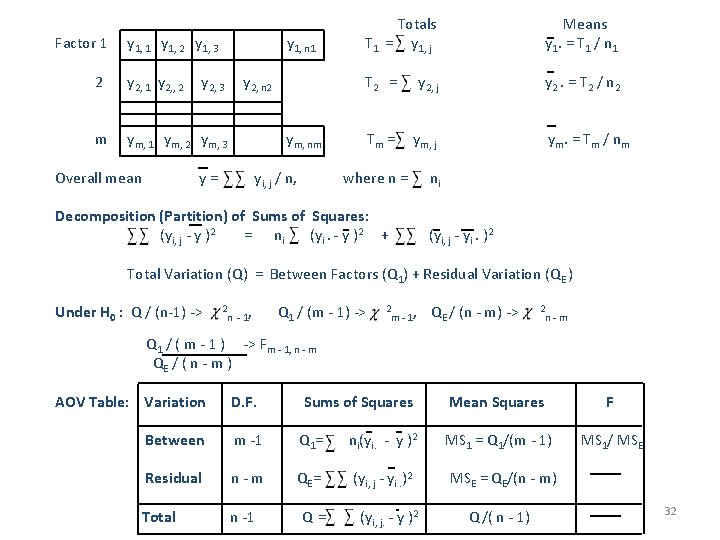
Factor 1 y 1, 2 y 1, 3 y 1, n 1 2 y 2, 1 y 2, , 2 m ym, 1 ym, 2 ym, 3 Overall mean y 2, 3 y 2, n 2 Totals T 1 = y 1, j Means y 1. = T 1 / n 1 T 2 = y 2, j y 2. = T 2 / n 2 Tm = ym, j ym, nm y= yi, j / n, where n = Decomposition (Partition) of Sums of Squares: (yi, j - y )2 = ni (yi. - y )2 + ym. = Tm / nm ni (yi, j - yi. )2 Total Variation (Q) = Between Factors (Q 1) + Residual Variation (QE ) Under H 0 : Q / (n-1) -> 2 n - 1, Q 1 / (m - 1) -> 2 m - 1, QE / (n - m) -> 2 n-m Q 1 / ( m - 1 ) -> Fm - 1, n - m QE / ( n - m ) AOV Table: Variation D. F. Sums of Squares Mean Squares F MS 1/ MSE Between m -1 Q 1 = ni(yi. - y )2 MS 1 = Q 1/(m - 1) Residual n-m QE= (yi, j - yi. )2 MSE = QE/(n - m) Total n -1 Q= (yi, j. - y )2 Q /( n - 1) 32

Two-Way Classification Factor II y 1, 1 y 1, 2 y 1, 3 : : : ym, 1 ym, 2 ym, 3 Means y. 1 y. 2 Partition SSQ: y 1, n : ym, n y. 3 yi, j = (yi, j - y )2 = n H 0 : All AOV + i are ym. y. n i + equal. y. . So we write as y (yi. - y )2 + m (y. j - y )2 + Total Variation Model: Means y 1. Between Rows j + H 0: all i, j , i, j j Between Columns (yi, j - yi. - y. j + y )2 Residual Variation ~ N ( 0, 2) are equal Variation D. F. Sums of Squares Mean Squares F Between m -1 Q 1= n (yi. - y )2 MS 1 = Q 1/(m - 1) MS 1/ MSE Rows Between n -1 Q 2= m (y. j - y )2 MS 2 = Q 2/(n - 1) MS 2/ MSE Columns Residual (m-1)(n-1) QE= (yi, j - yi. - y. j + y)2 MSE = QE/(m-1)(n-1) Total mn -1 Q= (yi, j. - y )2 Q /( mn - 1) 33

Two-Way Example Factor I Fact II 1 2 3 4 Totals Means 1 2 3 4 5 Totals Means 20 18 21 23 20 102 20. 4 19 18 17 18 18 90 18. 0 23 21 22 23 20 109 21. 8 17 16 18 16 17 84 16. 8 79 73 78 80 75 385 19. 75 18. 25 19. 50 20. 00 18. 75 19. 25 ANOVA outline Variation d. f. SSQ MSQ F Rows 3 76. 95 25. 65 18. 86** Columns 4 8. 50 2. 13 1. 57 Residual 12 16. 30 Total 19 101. 75 FYI software such as R, SAS, SPSS, MATLAB is designed for analysing these data, e. g. SPSS as spreadsheet recorded with variables in columns and individual observations in the rows. Thus the ANOVA data above would be written as a set of columns or rows, e. g. Var. value 20 18 21 23 20 19 18 17 18 18 23 21 22 23 20 17 16 18 16 17 Factor 1 1 1 2 2 2 3 3 3 4 4 4 Factor 2 1 2 3 4 1 2 3 4 34

‘BIO’ CONTEXT here • GENETICS : 5 branches; aim = ‘Laws’ of Chemistry, Physics, Maths. for Biology • GENOMICS : Study of Genomes (complete set of DNA carried by Gamete) by integration of 5 branches of Genetics with ‘Informatics and Automated systems’ • PURPOSE of GENOME RESEARCH : Info. on Structure, Function, Evolution of all Genomes – past and present • Techniques of Genomics from molecular, quantitative, population genetics: Concepts and Terminology from Mendelian genetics and cytogenetics 35

CONTEXT: GENETICS - BRANCHES • Classical Mendelian – Gene and Locus, Allele, Segregation, Gamete, Dominance, Mutation • Cytogenetics – Cell, Chromasome, Meiosis and Mitosis, Crossover and Linkage • Molecular – DNA sequencing, Gene Regulation and Transcription, Translation and Genetic Code Mutations • Population – Allelic/Genotypic Frequencies, Equilibrium, Selection, Drift, Migration, Mutation • Quantitative – Heritability/Additive, Non-additive Genetic Effects, Genetic by Environment Interaction, Plant and Animal Breeding 36

CONTEXT+ : GENOMICS -LINKAGES Mendelian Cytogenetics Molecular GENOMICS Genetic markers DNA Sequences Linkage/Physical Maps Population Gene Location QTL Mapping Quantitative 37

GENOMICS - FOCUS CLASSICAL Genetic Markers, Linkage Analysis, Gene Ordering, Multipoint Analysis, Genetic and QTL mapping INFORMATICS Databases, Sequence Comparison, Data Communications, Automation DNA SEQUENCE ANALYSIS Sequence Assembly, Placement, Comparison 38

GENOMICS – some KEY QUESTIONS • HOW do Genes determine total phenotype? • HOW MANY functional genes necessary and sufficient in a given system? • WHAT are necessary Physical/Chemical aspects of gene structure? • IS gene location in Genome specific? • WHAT DNA sequences/structures are needed for genespecific functions? • HOW MANY different functional genes in whole biosphere? • WHAT MEASURES of essential DNA sameness in different species? 39

‘DATA’ : STATISTICAL GENOMICS Some UNUSUAL/SPECIAL FEATURES • Size – databases very large e. g. molecular marker and DNA / protein sequence data • Mixtures of variables - discrete/continuous e. g. combination of genotypes of genetic markers (D) and values quantitative traits (C) • Empirical Distributions needed for some Test Statistics e. g. QTL analysis, H. T. of locus order • Intensive Computation e. g. Linkage Analysis, QTL and computationally greedy algorithms in locus ordering, derivation of empirical distributions etc. • Likelihood Analysis - Linear Models typically insufficient alone 40

‘BUSINESS’ CONTEXT here • http: //big. computing. dcu. ie/ • • • Data-rich environments – under-utilisation of resources RAW DATA into useful information and knowledge Similar underpinning: (‘Laws’)– based on analysis Purpose – Informed decision-making Techniques – quantitative. Concepts & Nature – Pervasive, Dynamic, ‘Health’ subject to Internal/External environments. Key elements - Systems and people 41

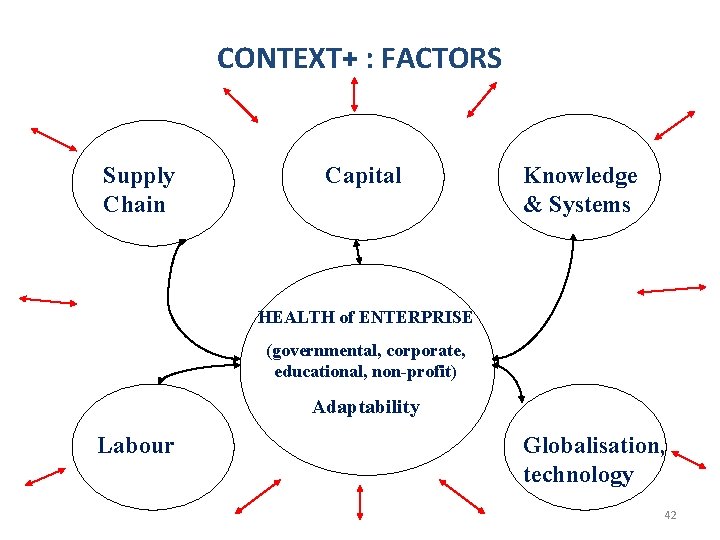
CONTEXT+ : FACTORS Supply Chain Capital Knowledge & Systems HEALTH of ENTERPRISE (governmental, corporate, educational, non-profit) Adaptability Labour Globalisation, technology 42

Framework • Status: Huge array of information systems and product software. q Challenges: include development, delivery, adoption, and implementation of IT solutions into usable and effective systems that mimic/support organisational processes. ‘KS alignment with work practice. ’ (Toffler & Drucker – 80’s : organisations of 20 th Century -> knowledge- based. Greater autonomy, revised management structures). q Opportunities: KM popularity grew through 90’s, spawned ideas of 'KM models', ‘KM strategy', concepts of 'organisational learning', 'knowledge /practice networks', 'knowledge discovery', ‘intellectual capital‘). • Objectives: To Plan, develop, implement, operate, optimise, cost information /communication systems and interpret use. • Starting point : understanding the opportunities of ICT for organisations requires both a technological and organisational perspective and an understanding of benefits associated with data capture and analysis. 43

Data Mining & KM • • • The Knowledge Discovery Process Classification e. g. clusters, trees Exploratory Data Analysis Models (including Bayesian Networks), Graphical or other. Frequent Pattern Mining and special groups/subgroups Key Features: • ‘Learning models’ from data can be an important part of building an intelligent decision support system. • Sophistication of analyses – computationally expensive data mining methods, complexity of algorithms, interpretation and application of models. 44

Hot Topics in BI • • • Business Process Management and Modelling Supply Chain Management and Logistics Innovation and ICT Analytical Information Systems, Databases and Data Warehousing Knowledge Management and Discovery Social Networks and Knowledge Communities • • • Performance Indicators &Measurement systems/Information Quality Data Analytics, Integration and Interpretation Cost-benefit and Impact Analysis Reference Models and Modelling Process Simulation and Optimization • Security and Privacy • IT and IS Architectures/Management • Info. Sys. development, Tools and Software Engineering 45

Example Questions • What are the characteristics of internet purchases for a given agegroup? How can this be used to develop further E-business? • What are key risk factors for profit/loss on a product on the basis of historical data and demographic variables? • Can we segment into/identify groups of similar on the basis of their characteristics and purchase behaviour? • Which products are typically bought together in one transaction by customers? • What are financial projections, given market volatility and knock-on for recent shock? • What data should an in-house information system collect? What design principles are involved for a large database? • What is involved in modelling and IT-supported optimisation of key business processes? 46