Data Abstraction Programming Language Essentials 2 nd edition

Data Abstraction Programming Language Essentials 2 nd edition Chapter 2. 2 An Abstraction for Inductive Data Types 1

define-datatype bintree: 'Number' | '(' 'Symbol' bintree ')' (define-datatype bintree? (leaf-node (datum number? )) (interior-node (key symbol? ) (left bintree? ) (right bintree? ))) predicate constructors 2

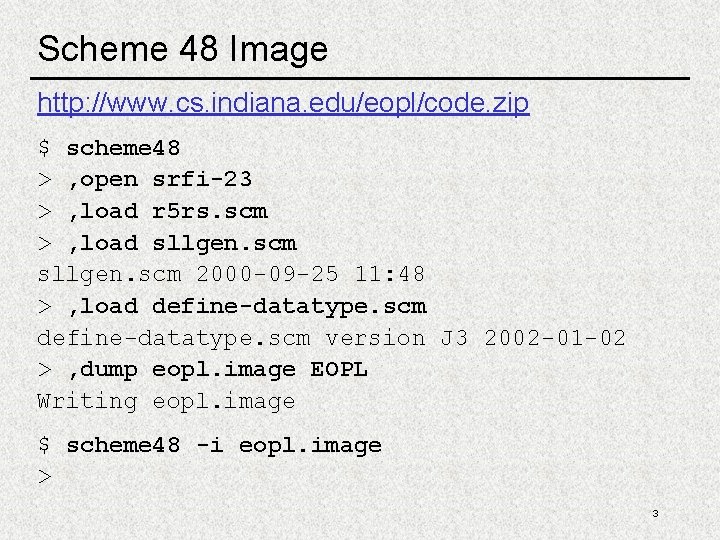
Scheme 48 Image http: //www. cs. indiana. edu/eopl/code. zip $ scheme 48 > , open srfi-23 > , load r 5 rs. scm > , load sllgen. scm 2000 -09 -25 11: 48 > , load define-datatype. scm version J 3 2002 -01 -02 > , dump eopl. image EOPL Writing eopl. image $ scheme 48 -i eopl. image > 3

Terminology aggregate: contains values of other types, e. g. , array or record with named fields. union: values are of other types. discriminated union: value contains explanatory tag and value of union's types. variant record: discriminated union of record types. Scheme values are discriminated union of primitive types. Inductively defined data types can be represented as variant records. 4

define-datatype Scheme extension (define-datatype-name type-predicate-name (variant-name (field-name predicate) … ) creates variant record type with one or more variants with zero or more fields type and variant names must be globally unique must be used at top level 5

define-datatype (2) creates type-predicate-name predicate with one argument creates variant-name constructor with one argument per field (define-datatype bintree? (leaf-node (datum number? )) (interior-node (key symbol? ) (left bintree? ) (right bintree? ))) 6

define-datatype (3) (leaf-node 29) (bintree? (leaf-node 29)) (interior-node 'foo (leaf-node 1) (leaf-node 2) ) (bintree? (interior-node 'foo (leaf-node 1) (leaf-node 2) ) ) 7

s-list: '(' symbol-expression* ')' symbol-expression: 'Symbol' | s-list (define-datatype s-list? (empty-s-list) (non-empty-s-list (first symbol-exp? ) (rest s-list? ))) (define-datatype symbol-exp? (symbol-exp (data symbol? )) (s-list-symbol-exp (data s-list? ))) 8

s-list based on Scheme lists (define-datatype s-list? (an-s-list (data (list-of symbol-exp? )))) (define list-of ; returns predicate for list (lambda (pred) (lambda (val) (or (null? val) (and (pair? val) (pred (car val)) ((list-of pred) (cdr val)) ) ) 9

Examples (s-list? (empty-s-list)) (s-list? (non-empty-s-list (symbol-exp 'a) (empty-s-list) ) ) (s-list? (an-s-list '())) (s-list? (an-s-list (symbol-exp 'a))) ) (s-list? (an-s-list (cons (symbol-exp 'a) '() ) 10

Sum of leaves of bintree (define leaf-sum (lambda (tree) (cases bintree (leaf-node (datum) (interior-node (key left right) (+ (leaf-sum left) (leaf-sum right)) ) ) (leaf-sum (interior-node 'foo (leaf-node 1) (leaf-node 2) ) ) 11

cases (cases type-name expression (variant-name (field-name …) body) … (else body) ) value of expression must be of type-name variant selects appropriate variant-name each field value is bound to field-name and body is executed without else, all variants must be specified 12

Lambda Calculus Representation expr: 'Symbol' | '(' 'lambda' '(' 'Symbol' ')' expr ')' | '(' expr ')' (define-datatype expression? (var-exp (id symbol? )) (lambda-exp (id symbol? ) (body expression? )) (app-exp (rator expression? ) (rand expression? ))) 13

Examples (expression? (var-exp 'x) ) (expression? (lambda-exp 'x (var-exp 'x)) ) (expression? (app-exp (var-exp 'f) (var-exp 'x)) ) (expression? (lambda-exp 'x (app-exp (var-exp 'f) (var-exp 'x)) ) ) 14

Syntax and Representation BNF specifies concrete syntax, external representation define-datatype defines building blocks for abstract syntax, internal representation expr: 'Symbol' var-exp (id) | '(' 'lambda' '(' 'Symbol' ')' expr ')' lambda-exp (id body) | '(' expr ')' app-exp (rator rand) 15

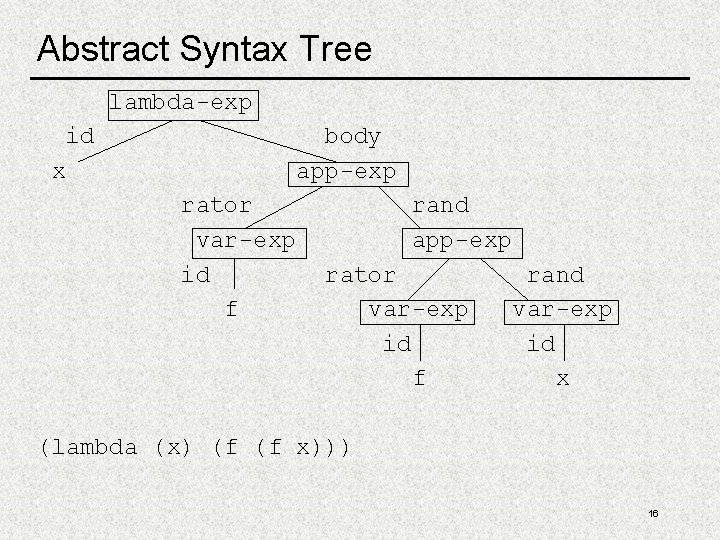
Abstract Syntax Tree lambda-exp id body app-exp x rator var-exp id f rand app-exp rator var-exp id f rand var-exp id x (lambda (x) (f (f x))) 16

Programming without an AST (define occurs-free? (lambda (var exp) (cond ((symbol? exp) (eqv? var exp)) ((eqv? (car exp) 'lambda) (and (not (eqv? (caadr exp) var)) (occurs-free? var (caddr exp)))) (else (or (occurs-free? var (car exp)) (occurs-free? var (cadr exp)) ) ) plagued by c*r references 17

Programming with an AST (define occurs-free? (lambda (var exp) (cases expression exp (var-exp (id) (eqv? id var)) (lambda-exp (id body) (and (not (eqv? id var)) (occurs-free? var body))) (app-exp (rator rand) (or (occurs-free? var rator) (occurs-free? var rand) ) ) 18

Example (occurs-free? 'f (lambda-exp 'x (app-exp (var-exp 'f) (var-exp 'x)) ) ) 19

unparse-expression (define unparse-expression (lambda (exp) (cases expression exp (var-exp (id) (lambda-exp (id body) (list 'lambda (list id) (unparse-expression body) ) ) (app-exp (rator rand) (list (unparse-expression rator) (unparse-expression rand) ) ) 20

Example (unparse-expression (lambda-exp 'x (app-exp (var-exp 'f) (var-exp 'x)) ) ) 21

parse-expression (define parse-expression (lambda (datum) (cond ((symbol? datum) (var-exp datum)) ((pair? datum) (if (eqv? (car datum) 'lambda) (lambda-exp (caadr datum) (parse-expression (caddr datum))) (app-exp (parse-expression (car datum)) (parse-expression (cadr datum)) ) (else (error 'parse-expression datum)) ) 22

Example (unparse-expression (parse-expression '(lambda (x) (f x)) ) ) 23