Data Abstraction and Problem Solving with JAVA Walls

Data Abstraction and Problem Solving with JAVA Walls and Mirrors Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Algorithm Efficiency and Sorting Data Abstraction and Problem Solving with JAVA: Walls and Mirrors Carrano / Prichard

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 1 Time requirements as a function of the problem size n

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 2 When n ≥ 2, 3 * n 2 exceeds n 2 - 3 * n + 10

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 3 a A comparison of growth-rate functions: a) in tabular form

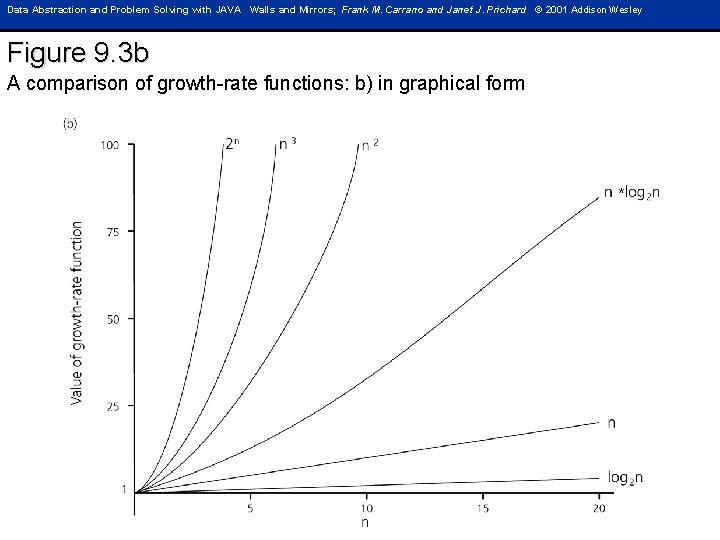
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 3 b A comparison of growth-rate functions: b) in graphical form

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 4 A selection sort of an array of five integers

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 5 The first two passes of a bubble sort of an array of five integers: a) pass 1; b) pass 2

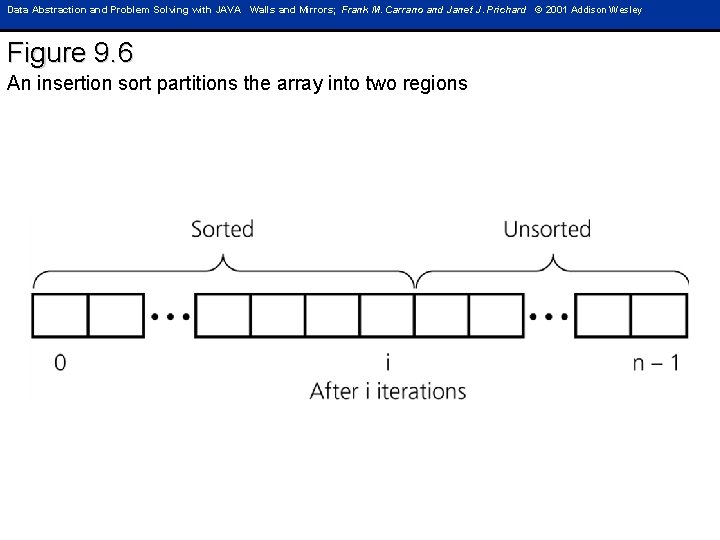
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 6 An insertion sort partitions the array into two regions

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 7 An insertion sort of an array of five integers.

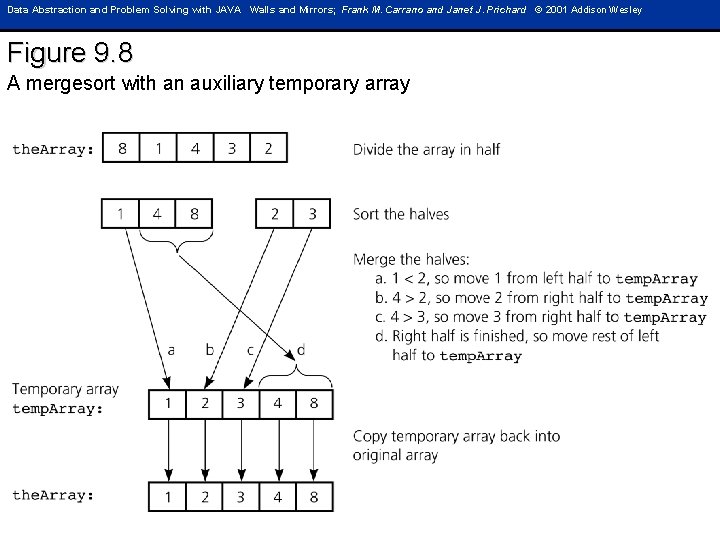
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 8 A mergesort with an auxiliary temporary array

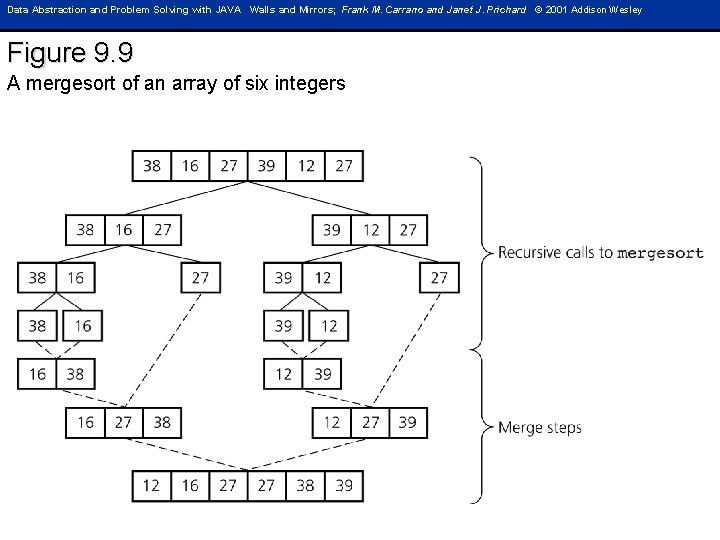
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 9 A mergesort of an array of six integers

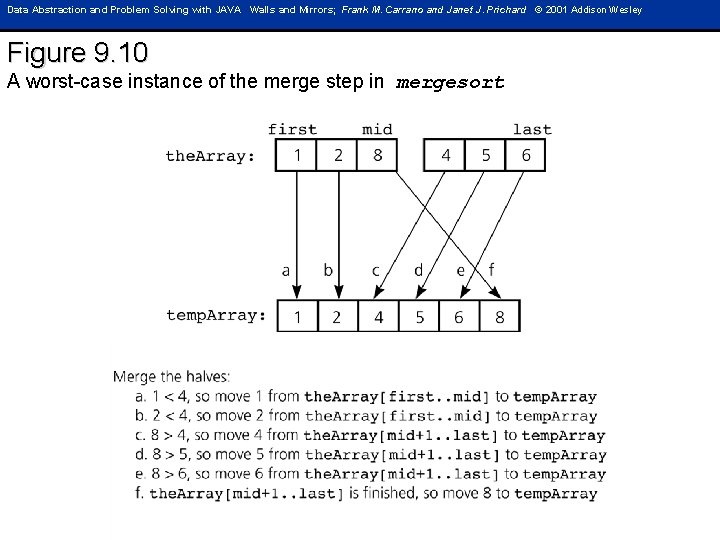
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 10 A worst-case instance of the merge step in mergesort

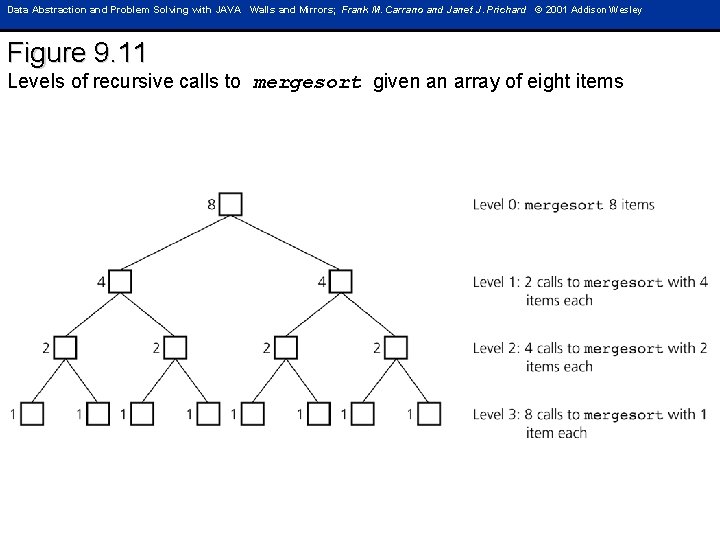
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 11 Levels of recursive calls to mergesort given an array of eight items

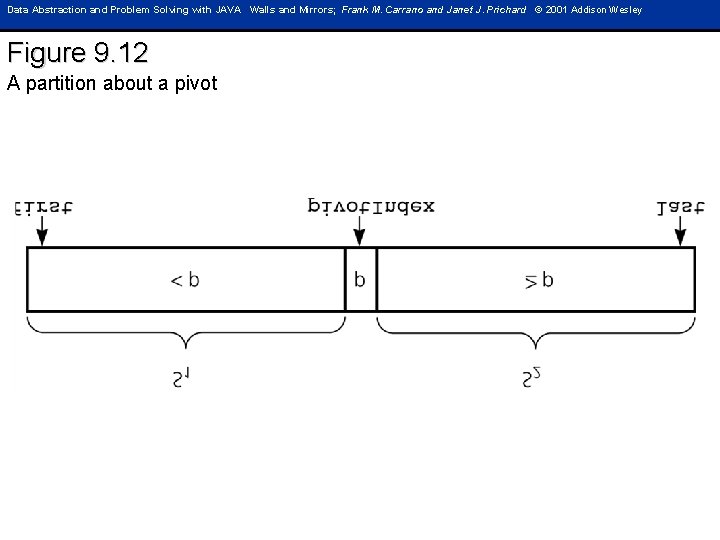
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 12 A partition about a pivot

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 13 k. Small versus quicksort

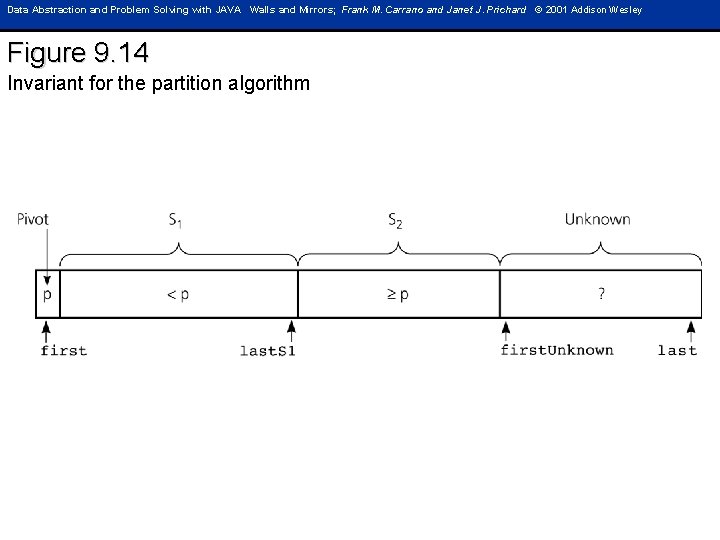
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 14 Invariant for the partition algorithm

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 15 Initial state of the array

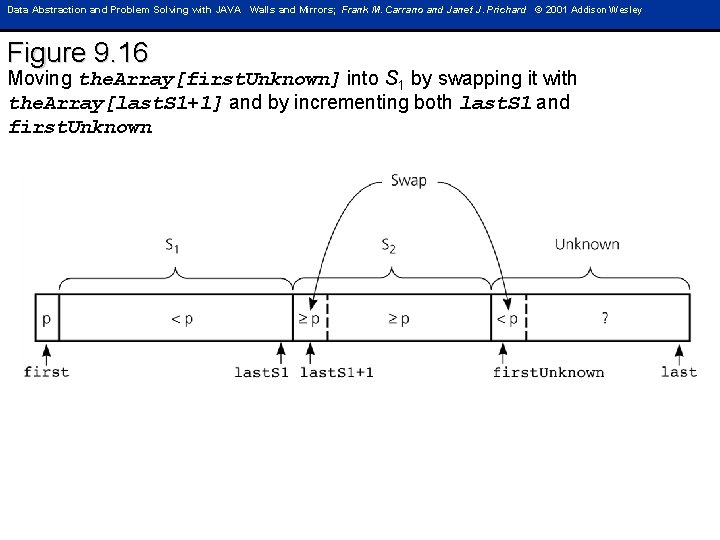
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 16 Moving the. Array[first. Unknown] into S 1 by swapping it with the. Array[last. S 1+1] and by incrementing both last. S 1 and first. Unknown

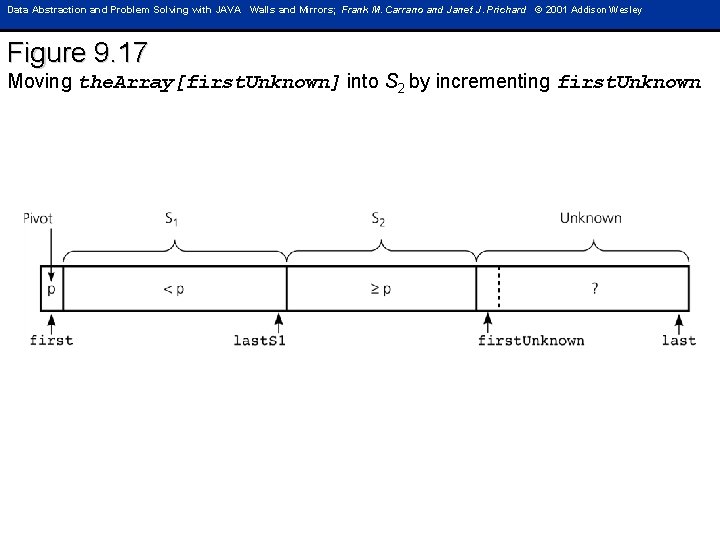
Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 17 Moving the. Array[first. Unknown] into S 2 by incrementing first. Unknown

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 18 a Developing the first partition of an array when the pivot is the first item

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 18 b Developing the first partition of an array when the pivot is the first item

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 19 A worst-case partitioning with quicksort

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 20 A average-case partitioning with quicksort

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 21 A radix sort of eight integers

Data Abstraction and Problem Solving with JAVA Walls and Mirrors; Frank M. Carrano and Janet J. Prichard © 2001 Addison Wesley Figure 9. 22 Approximate growth rates of time required for eight sorting algorithms