Darcys Law and its validity In 1856 Henri





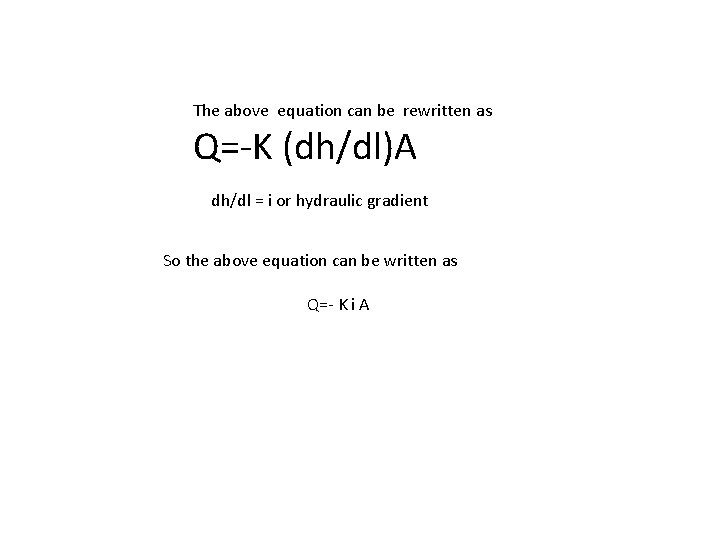






- Slides: 14

Darcy’s Law and its validity

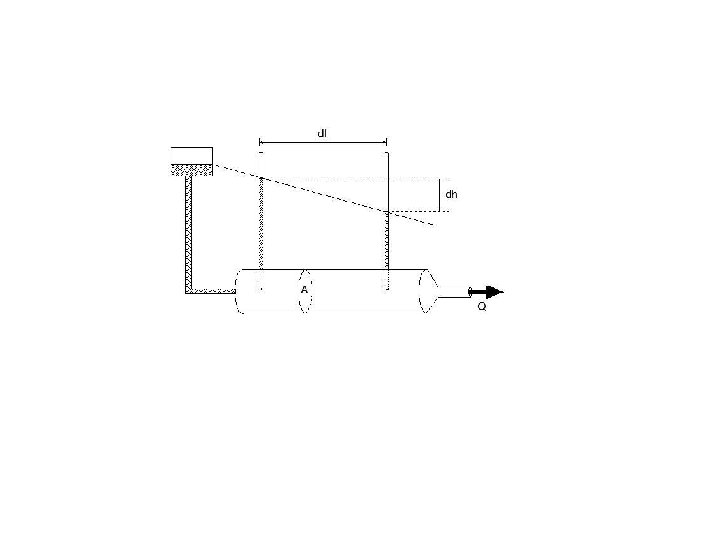
In 1856, Henri Darcy experimented with fluid flow through a pipe filled with sand (Figure 3 -5 a). He forced water through the pipe under a hydraulic head (i. e. , he filled up a reservoir at a higher elevation than the pipe and allowed gravity to drive water through the sand) and he measured: -the rate of discharge through the pipe (Q) - the loss in head (dh) across some length of the pipe (dl).


He concluded that • discharge of water through the pipe is directly proportional to the head loss. • and inversely proportional to the length of the path of flow (Figure above). • Or he concluded that the discharge is directly proportional to the hydraulic gradient. Head loss is the difference between the head of two piezometers- which is Shown as dh in the figure above. Length of the flow path is shown as dl in the figure above.

This statement is written as - Here Q is the discharge A is the area K is the hydraulic conductivity or here is the proportionality Constant.

If we divide through by the cross-sectional area, the volumetric discharge reduces down to a 1 -dimensional discharge (i. e. , velocity) called the darcian velocity (q), or: the specific discharge is q or v - in some book it is denoted by “q” and in some by “v” q=v= Q/A the dimensions of Q are [L 3 /T] and those of A are [L 2], v has the dimensions of a velocity [L/T].
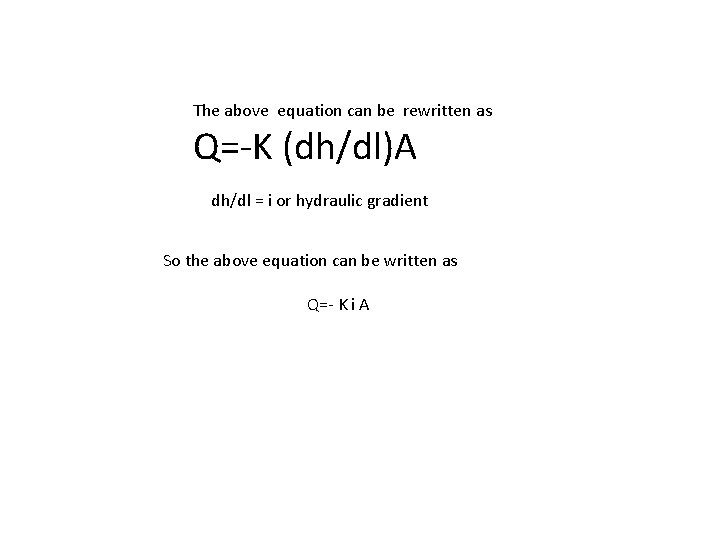
The above equation can be rewritten as Q=-K (dh/dl)A dh/dl = i or hydraulic gradient So the above equation can be written as Q=- K i A

Validity of Darcy’s Law One of the assumptions inherent in Darcy’s law is the assumption of laminar flow. Darcy’s law is not valid above the onset of turbulence in the system, because the discharge is no longer linearly proportional to the gradient.

The upper limit is usually identified with the aid of the Reynolds number Re, a dimensionless number that expresses the ratio of inertial to viscous forces. The Reynolds number for flow through porous media is defined as Where - p is fluid density: -and μ is the dynamic viscosity of the fluid, -v the, specific discharge/fluid velocity and -d a representative length dimension for the porous medium,

Reynold number is equal to inertial forces acting on the system divided by the viscous forces- as given in the earlier equation. When the Reynold ‘s number is less or equal to 1 –here darcy’s Is valid If Reynold’s number is 1 to 10 there is no violation or it is transient flow. Beyond 10 the flow is turbulent and Darcy’ law can not be applied.

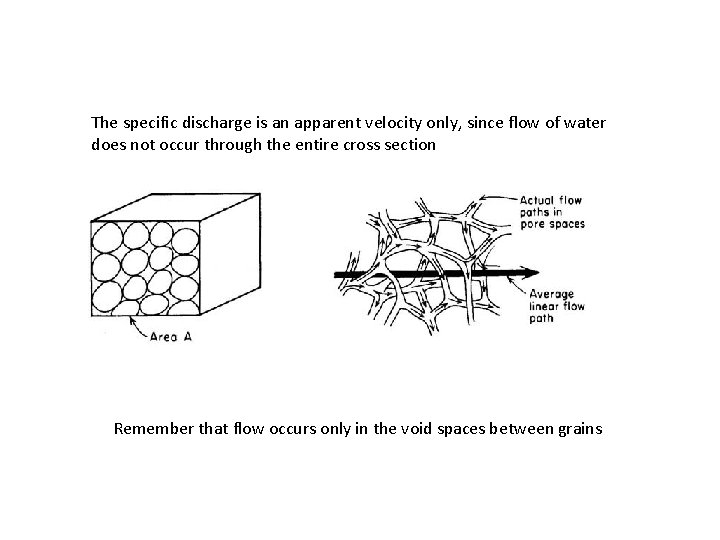
Specific Discharge and Average Linear Velocity Q The specific discharge (Darcian velocity), q, of groundwater is equal to Q/A:

The specific discharge is an apparent velocity only, since flow of water does not occur through the entire cross section Remember that flow occurs only in the void spaces between grains

Hence, the specific discharge given by equation below underestimates the actual velocity of water moving through the void spaces. To find the actual average linear velocity, v, at which the water is moving, one divides the specific discharge by the porosity (n) to account for the actual open space available for flow: The average linear velocity is extremely important. It is the value used to determine how long it would take a contaminant to move from point A to point B in an aquifer.

Reference: -Groundwater by Freeze and cherry -Hydrogeology Lecture Notes by Matthew M. Uliana,