Daniel S Yates The Practice of Statistics Third

Daniel S. Yates The Practice of Statistics Third Edition Chapter 1: Exploring Data 1. 2 Describing Distributions with Numbers Copyright © 2008 by W. H. Freeman & Company

Objectives for 1. 2 • Given a data set, How do you compute mean, median, quartiles, and the five-number summary? • How do you construct a box plot using the fivenumber summary? • How do you compute the inter-quartile range? • How do you identify an outlier using the interquartile range rule? • How do you compute the standard deviation and variance?

Measure for The Center of a Distribution

The Means of a Data Set • So far, we know several measures of central tendency of a set of numbers: means, median, and mode. • The means is the arithmetic average of the data set.

The Mean of a Data Set “Average Value” • Σ (sigma) means to add them all up. All the data values and get a total. • Take the total and divide by the number of data.

Example - Mean • Joey’s first 14 quiz grades in a marking period were 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 • Find the mean. • Answer 85. • Use calculator – Stat edit, enter data in L 1 Second Stat, Math, Mean( L 1), Enter

The Median of the Data Set • Median is the center of the data set. • Half of the data set is above and Half is below the median. The 50 th Percentile. • The median may or may not be in the data set.

Calculation for Median “Middle Value”

Example - Median • Joey’s first 14 quiz grades in a marking period were 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 • Find the median. • Answer 85. • Use calculator – Stat edit, enter data in L 1 Second Stat, Math, Median( L 1), Enter

Terminology “A measure is resistant” • A measure that does not respond strongly to the influence of outliers (extreme observations). • Furthermore, a measure that is resistant does not respond strongly to changes in a few observations.

Are mean and median resistant? Mean and Median Applet

Mean vs Median • Mean is not a resistant measure. – It is sensitive to the influence of a few extreme observations (outliers). – It is sensitive to skewed distributions. The mean is pulled towards the tail. • Median is resistant. – It is resistant to extreme values and skewed distributions. • For skewed distributions the median is the better measure for center.

Measure for Spread Range Quartiles Five Number Summary The Standard Deviation

Range • The difference between the largest value and the smallest value. • Gives the full spread of the data. • But may be dependent on outliers.

Quartiles • We can describe the spread (variability of a distribution) by giving several percentiles (pth percentile of a distribution) • Typically we use 25 th percentile, 50 th percentile, 75 th percentile. • Q 1, median, Q 3.

Example • Joey’s first 14 quiz grades in a marking period were 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 • Find Q 1, median, and Q 3. • Answer: Q 1 = 78, Median = 85, Q 3 = 91 • Using the calculator – STAT, CALC, 1 -Var Stats L 1, ENTER

Five Number Summary Using the calculator, we again use 1 -Var Stats.

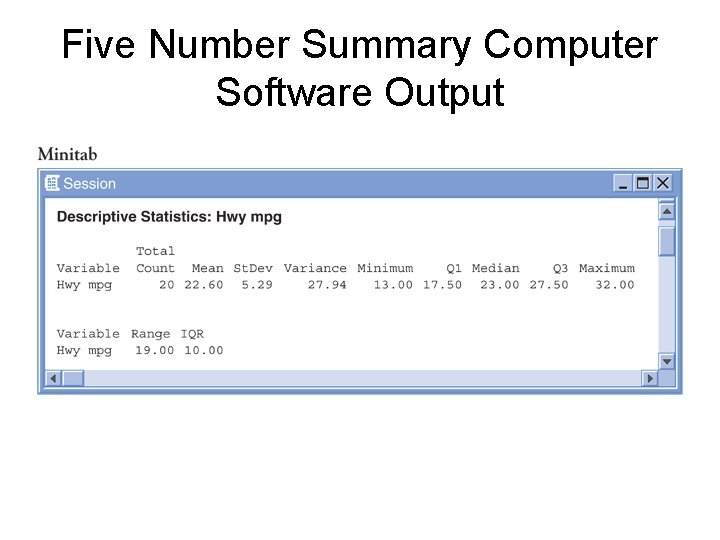
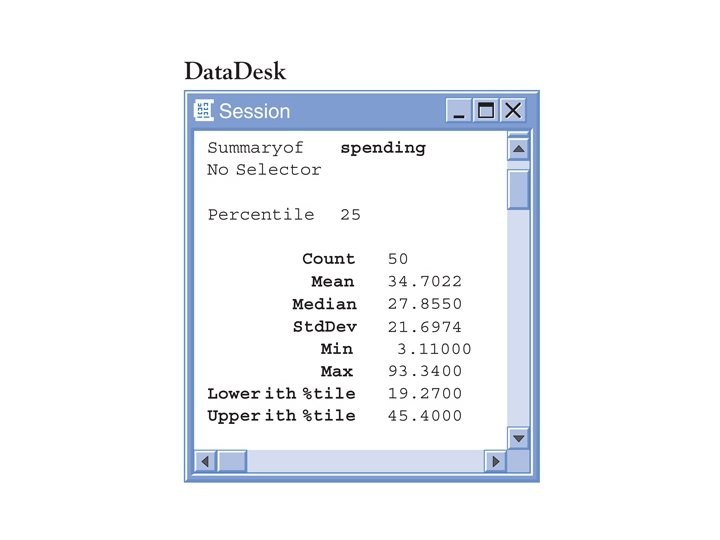
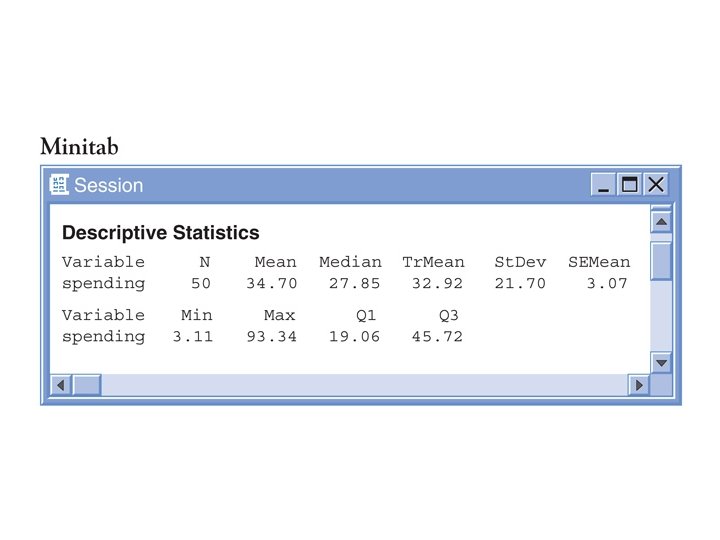
Five Number Summary Computer Software Output

Five Number Summary Computer Software Output

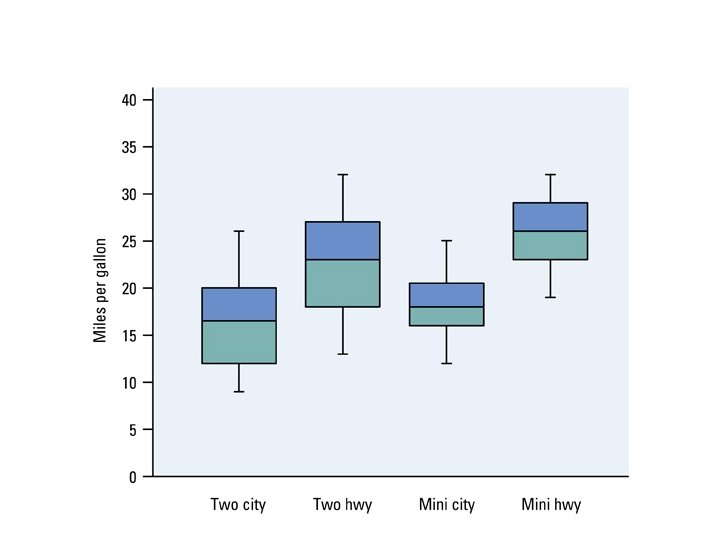
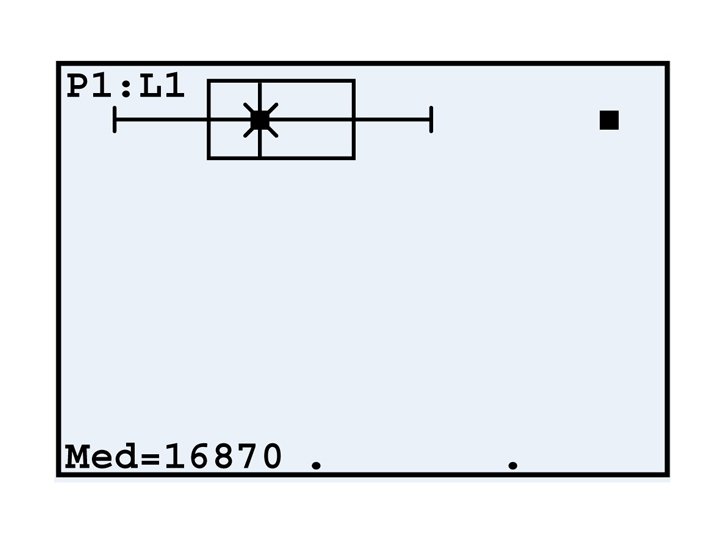
Graphical Display of 5 Number Summary

Example - Boxplot • Joey’s first 14 quiz grades in a marking period were 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 • Answer 74 78 85 91 98 • Calculator STAT PLOT, make appropriate selections on the menu, ZOOM, 9: Zoom Stat

Interquartile Range

Identifying Outliers

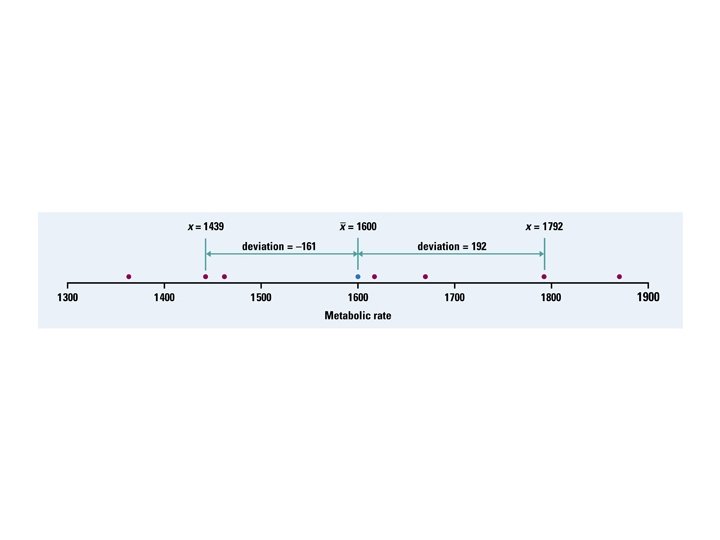
Variance and Standard Deviation

Example – Variance and Standard 86 86 -85=1 1 Deviation 84 84 -85=-1 1 Joey’s first 14 quiz grades in a marking period were 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 91 91 -85=6 36 75 75 -85=-10 100 Calculate the variance and standard deviation. 78 78 -85=-7 49 80 80 -85=-5 25 74 74 -85=-11 121 87 87 -85=2 4 76 76 -85=-9 81 96 96 -85=11 121 82 82 -85=-3 9 90 90 -85=5 25 98 98 -85=13 169 93 93 -85=8 64 Standard Deviation Calculator – STAT EDIT, enter data in list 1, QUIT STAT CALC 1 -Var Stat Total 1190 Tot 806

Standard Deviation • The standard deviation is zero when there is no spread. • The Standard deviation gets larger as the spread increases.

Impact of adding a constant to all data in the set? • Joey’s first 14 quiz grades in a marking period were – 86, 84, 91, 75, 78, 80, 74, 87, 76, 96, 82, 90, 98, 93 • Add 32 points to each score, then store in L 2. • Compute 1 -Var Stat. What has changed? • The five-number summary has changed but the standard deviation has not? • The measure the spread remains the same?

The impact of multiplying each data in the set by a constant? • • Using the data set in L 1 multiply the 2. Compute 1 -Var Stat. What has changed? The five-number summary has changed by 2 times and the standard deviation has changed by 2 times. • The measure of the spread has increased.