Daniel S Yates The Practice of Statistics Chapter

Daniel S. Yates The Practice of Statistics Chapter 9: 9. 1 Sampling Distributions Copyright © 2008 by W. H. Freeman & Company

Essential Questions for 9. 1 • • What is a parameter? What is a statistics? What is sampling variability? What is a sampling distribution? How do you describe a sampling distribution? • What is an unbiased statistic and an unbiased estimator?

Definitions • parameter: – a number that describes the population – a parameter is a fixed number – in practice, we do not know its value because we cannot examine the entire population

Definitions • statistic: – a number that describes a sample – the value of a statistic is known when we have taken a sample, but it can change from sample to sample – we often use a statistic to estimate an unknown parameter

Compare • parameter – mean: μ – standard deviation: σ – proportion: p • statistic – mean: x-bar – standard deviation: s – proportion: (p-hat) • Sometimes we call the parameters “true”; true statistics “sample”; mean, true proportion, sample mean, sample etc. proportion, etc.

Sampling Variability • Question: What would happen if we took many sample? • To answer this question, we would do the following: – Take a large number of samples from the same population. – Calculate the sample means or the sample proportion for each sample. – Make a histogram. – Examine the distribution for shape, center, spread and outliers. • In Practice it is too expensive to take many samples from a population. Simulation may be used instead of many samples to approximate the sampling distribution. • Probability may be used to obtain an exact sampling distribution without simulation.

Sampling Distributions • The sampling distribution of a statistic is the distribution of values taken by the statistic in all possible samples of the same size from the same population.

• http: //www. ruf. rice. edu/~lane/stat_sim/sam pling_dist/

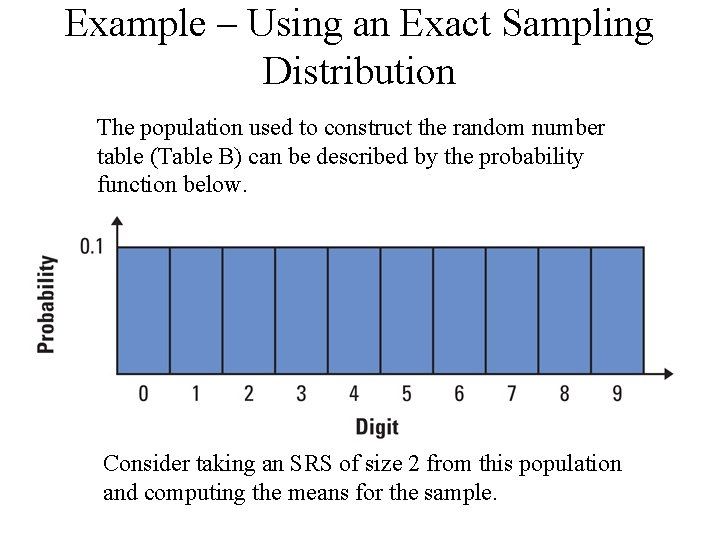
Example – Using an Exact Sampling Distribution The population used to construct the random number table (Table B) can be described by the probability function below. Consider taking an SRS of size 2 from this population and computing the means for the sample.

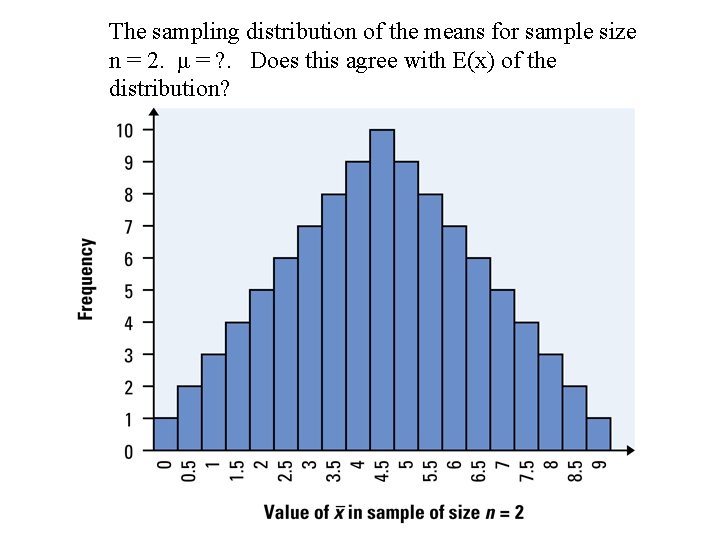
Instead of doing a simulation we can construct the actual sampling distribution displayed below. Using this table we can construct a sampling distribution.

The sampling distribution of the means for sample size n = 2. μ = ? . Does this agree with E(x) of the distribution?

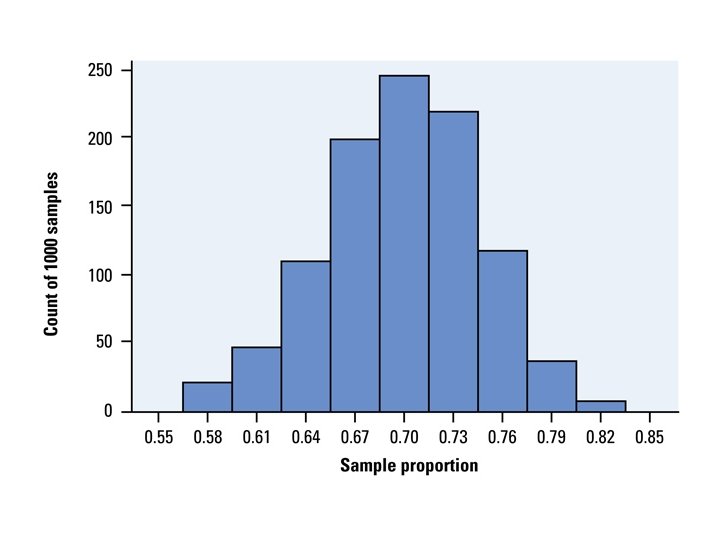
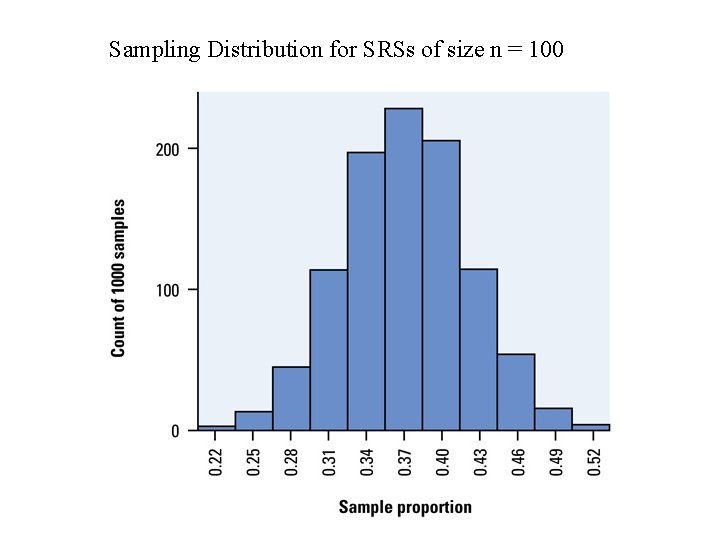
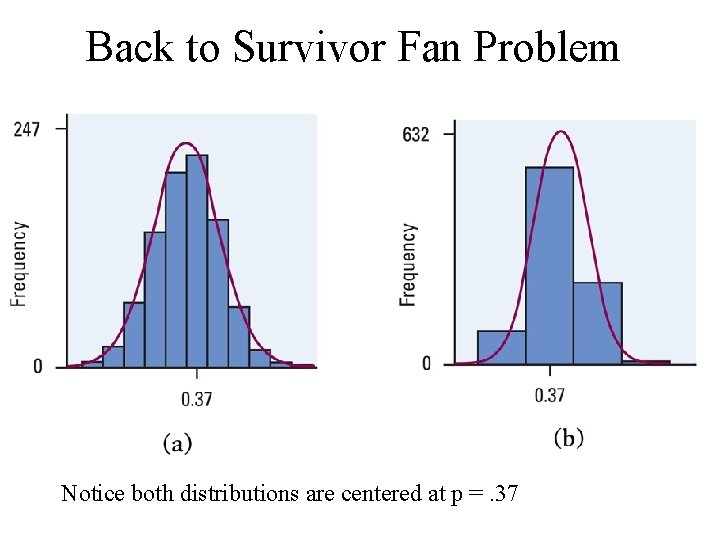
Example –Survivor Fan? • Television executives and companies who advertise on TV are interested in how many viewers watch particular television shows. According to 2001 Nielsen ratings, Survivor II was one of the most watched television shows in the US during every week that is aired. • Suppose that true proportion of US adults who watched Survivor II is p=. 37. • Suppose we did a survey with n=100. • Suppose we did this survey 1000 times.

Sampling Distribution for SRSs of size n = 100

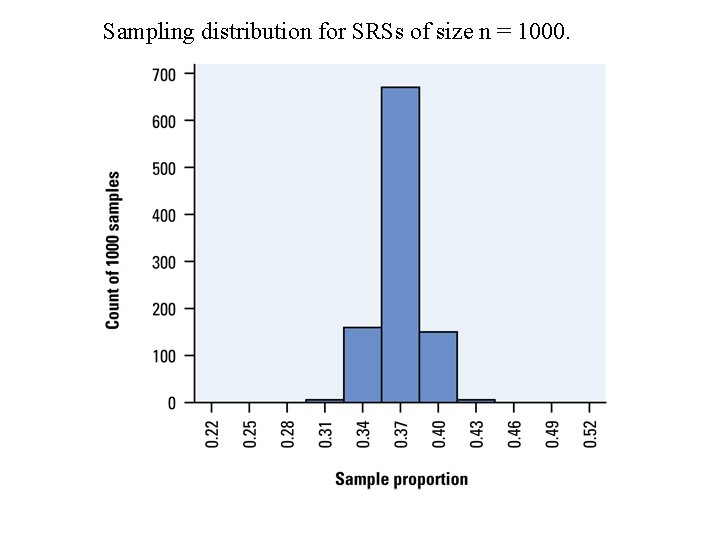
Sampling distribution for SRSs of size n = 1000.

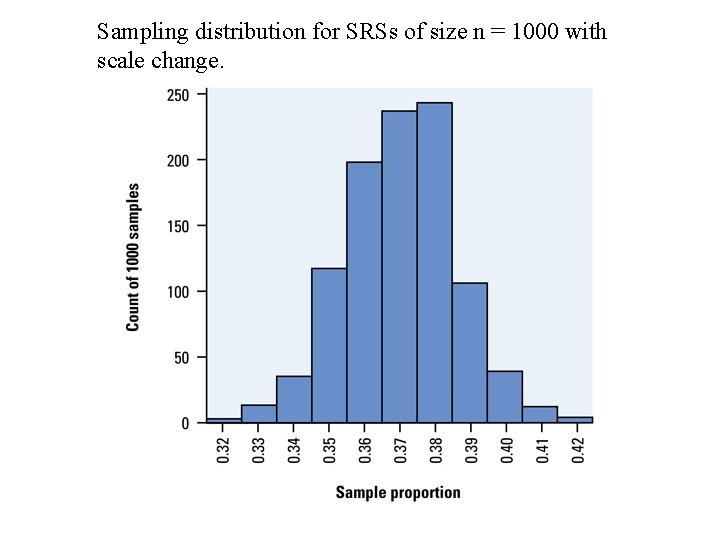
Sampling distribution for SRSs of size n = 1000 with scale change.

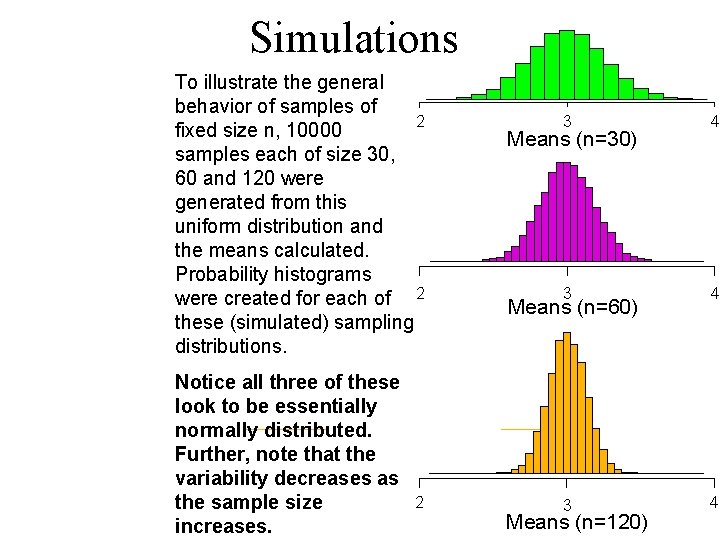
Simulations To illustrate the general behavior of samples of 2 fixed size n, 10000 samples each of size 30, 60 and 120 were generated from this uniform distribution and the means calculated. Probability histograms were created for each of 2 these (simulated) sampling distributions. Notice all three of these look to be essentially normally distributed. Further, note that the variability decreases as 2 the sample size increases. 3 4 3 4 Means (n=30) Means (n=60) Means (n=120)

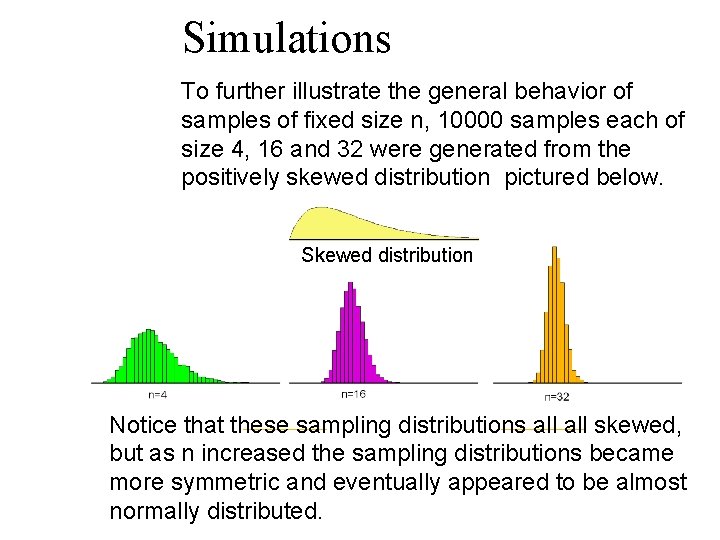
Simulations To further illustrate the general behavior of samples of fixed size n, 10000 samples each of size 4, 16 and 32 were generated from the positively skewed distribution pictured below. Skewed distribution Notice that these sampling distributions all skewed, but as n increased the sampling distributions became more symmetric and eventually appeared to be almost normally distributed.

Back to Survivor Fan Problem Notice both distributions are centered at p =. 37

Survivor Fan • Because the sampling distribution is centered at the true value, there is no systematic tendency to overestimate or underestimate the paramater p.

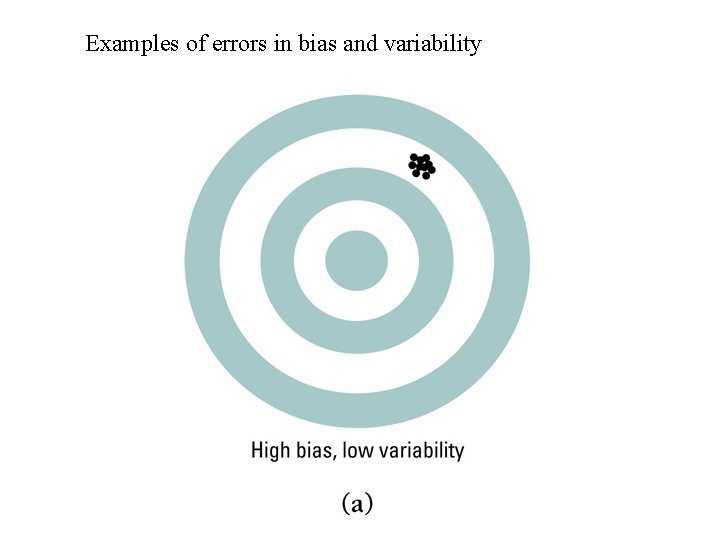
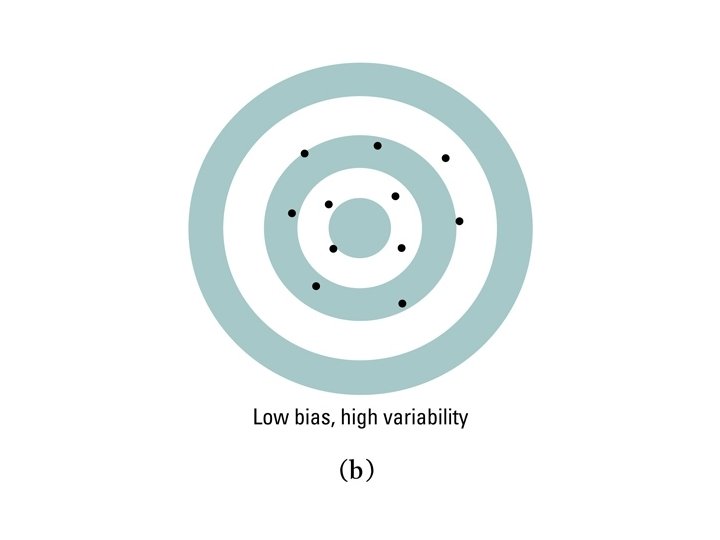
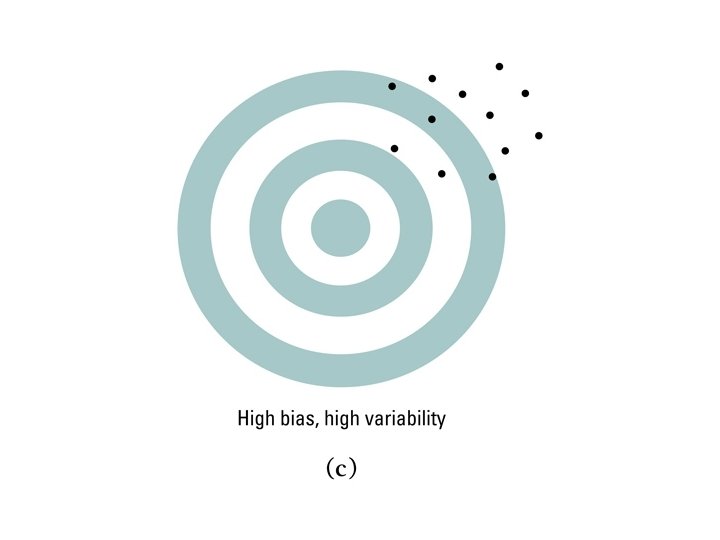
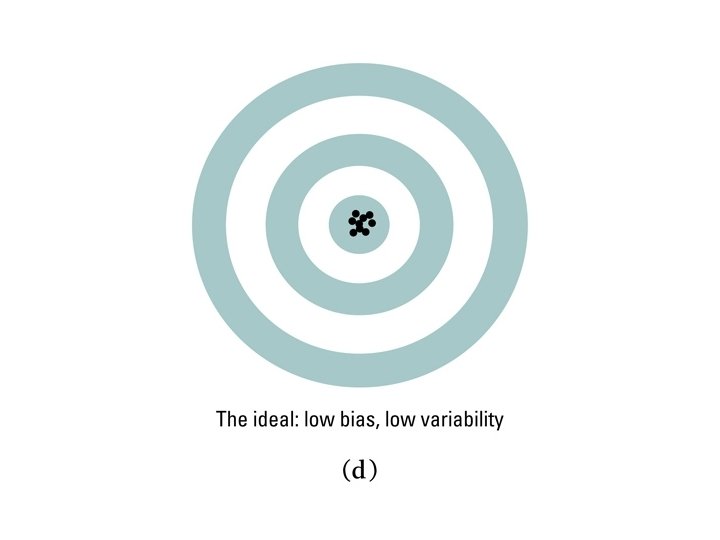
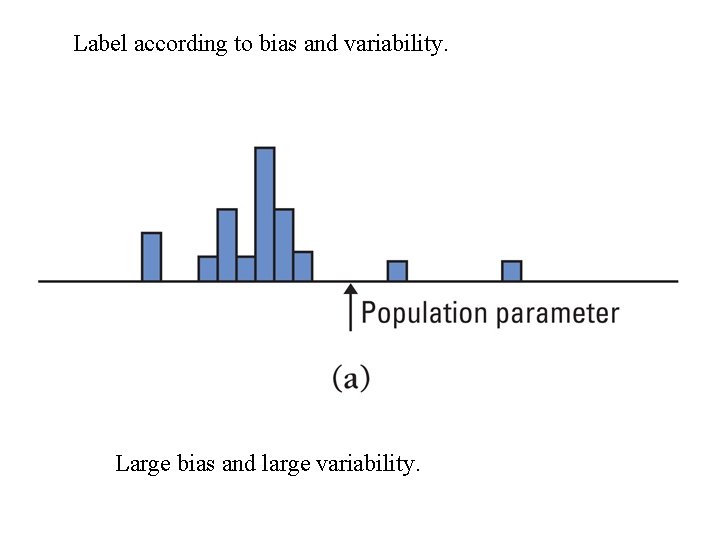
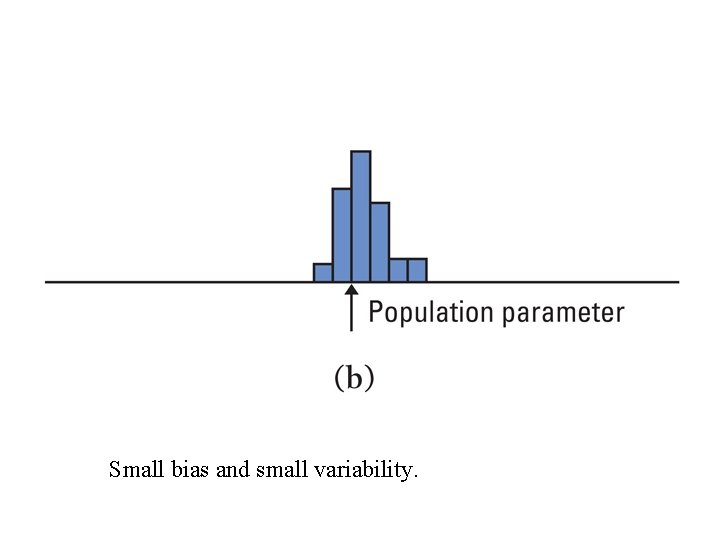
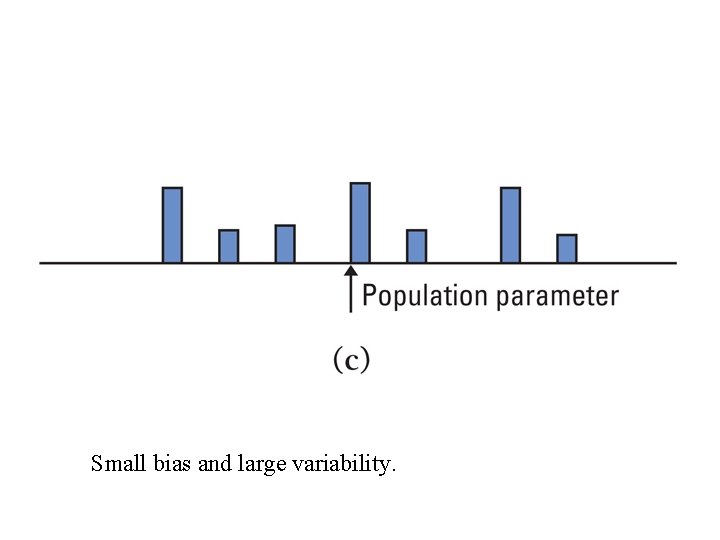
Examples of errors in bias and variability

Label according to bias and variability. Large bias and large variability.

Small bias and small variability.

Small bias and large variability.

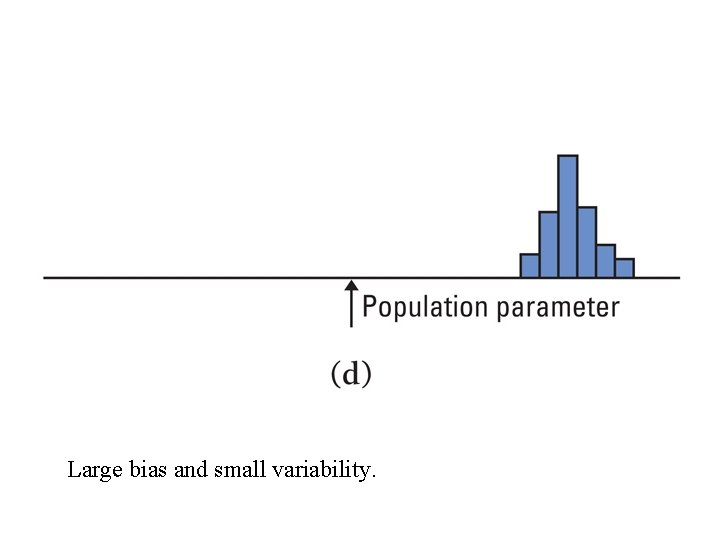
Large bias and small variability.

Essential Questions for 9. 1 • • What is a parameter? What is a statistics? What is sampling variability? What is a sampling distribution? How do you describe a sampling distribution? • What is an unbiased statistic and an unbiased estimator?