Damped Oscillations 11302020 Damped Oscillations 1 Free Damped











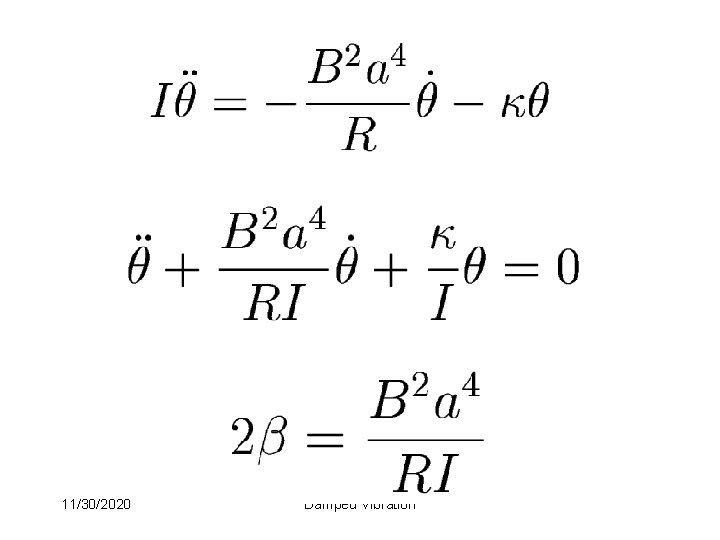










- Slides: 37

Damped Oscillations 11/30/2020 Damped Oscillations 1

(Free) Damped Oscillations The equation of motion is Let us now find out the solution 11/30/2020 Damped Oscillations 2

Try a solution In the equation Substitution yields 11/30/2020 Damped Oscillations 3

The equation has the roots and 11/30/2020 Damped Oscillations 4

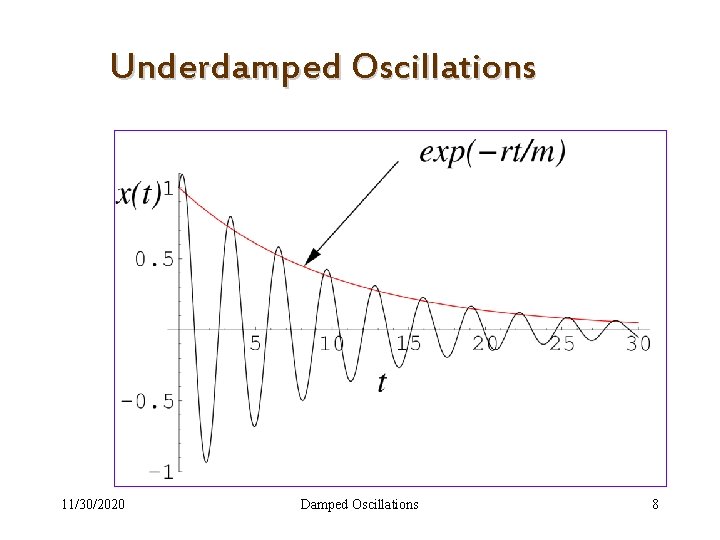
Situation 1: Underdamped or let us call then the roots are then the general solution 11/30/2020 Damped Oscillations 5

General solution: Underdamped 11/30/2020 Damped Oscillations 6

Different Initial Conditions Case-1. Released from extremity 11/30/2020 Damped Oscillations 7

Underdamped Oscillations 11/30/2020 Damped Oscillations 8

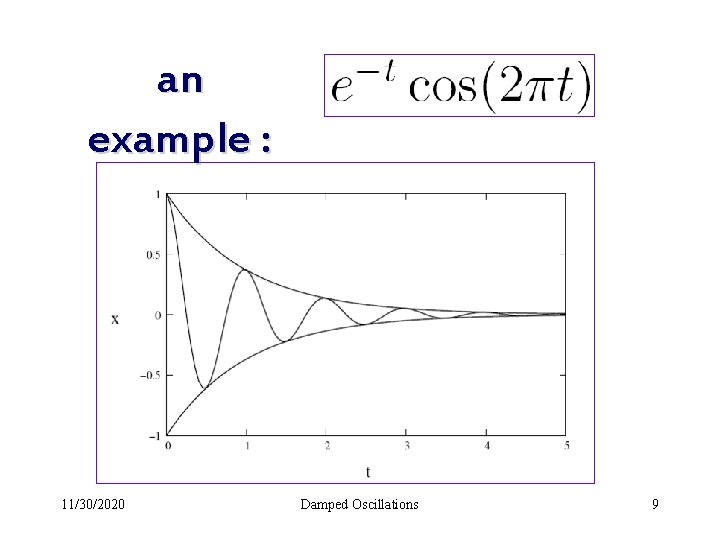
an example : 11/30/2020 Damped Oscillations 9

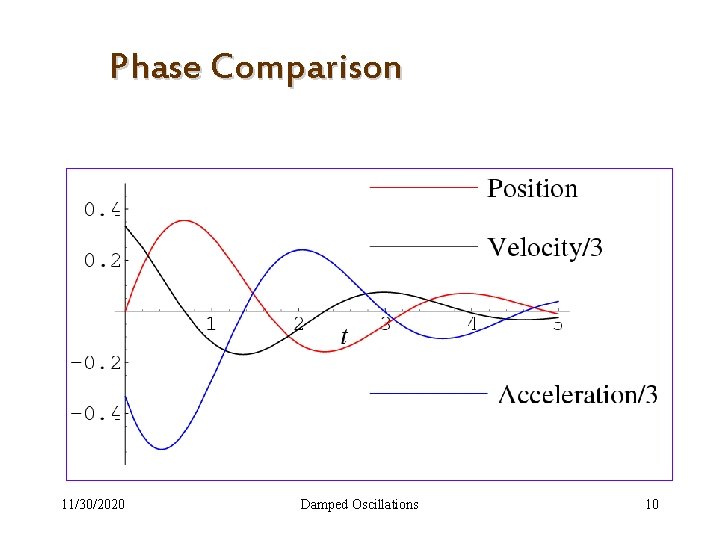
Phase Comparison 11/30/2020 Damped Oscillations 10

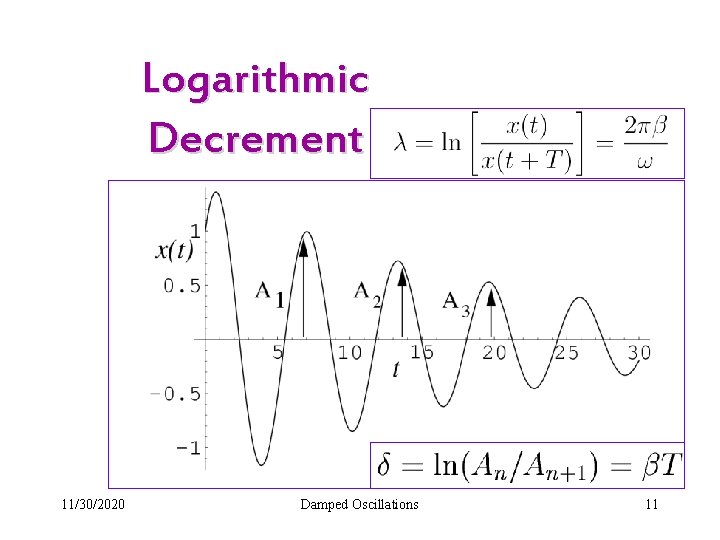
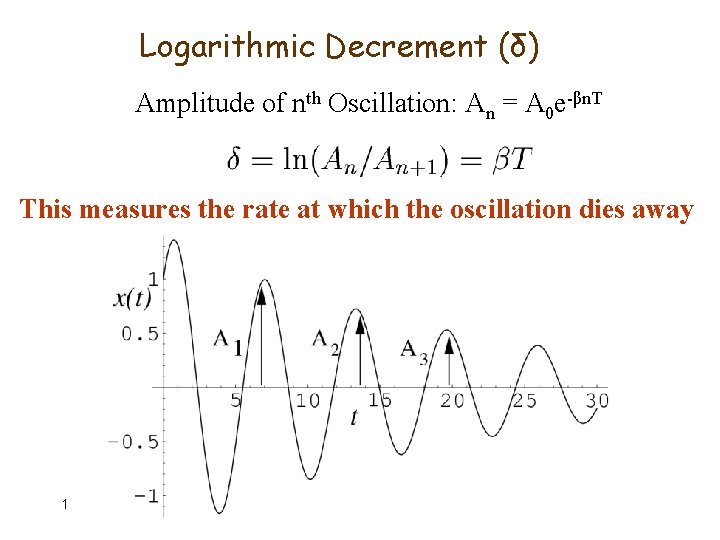
Logarithmic Decrement 11/30/2020 Damped Oscillations 11

How to describe the damping of an Oscillator q What is the rate of amplitude dying ? Logarithmic decrement q. What is the time taken by amplitude to decay to 1/e (=0. 368) times of its original value ? Relaxation time q. What is the rate of energy decaying to 1/e (=0. 368) times of its original value ? Quality Factor The time for a natural decay process to reach zero is theoretically infinite. Measurement in terms of the fraction e-1 of the original value is a very common procedure in Physics. 11/30/2020 Damped Vibration

Logarithmic Decrement (δ) Amplitude of nth Oscillation: An = A 0 e-βn. T This measures the rate at which the oscillation dies away 11/30/2020 Damped Vibration

Relaxation time (τ) Amplitude : A = A 0 e-βt ; at t=0, A=A 0 (1/e)A 0 = A 0 e-βτ Quality factor (Q) Energy : ½k(Amplitude)2 ; E=E 0 e-2βt (1/e)E 0 = E 0 e-2β(Δt) ; Δt = 1/2β Q = ω´Δt = ω´/2β = π/δ Quality factor is defined as the angle in radians through which the damped system oscillates as its energy decays to e-1 of its original energy. Show that Q = 2π (Energy stored in system/Energy lost per cycle) 11/30/2020 Damped Vibration

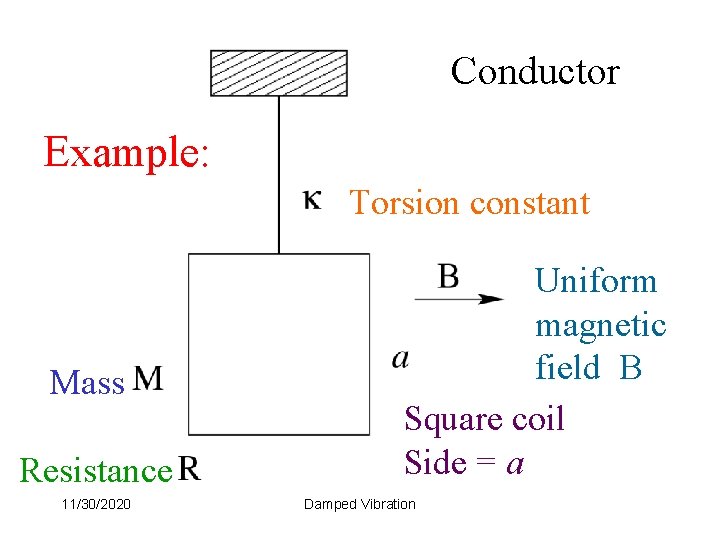
Example: LCR in series Find charge on the capacitor at time t. 11/30/2020 Damped Vibration

Example: LCR in series Find charge on the capacitor at time t. 11/30/2020 Damped Vibration

Conductor Example: Torsion constant Mass Resistance 11/30/2020 Uniform magnetic field B Square coil Side = a Damped Vibration

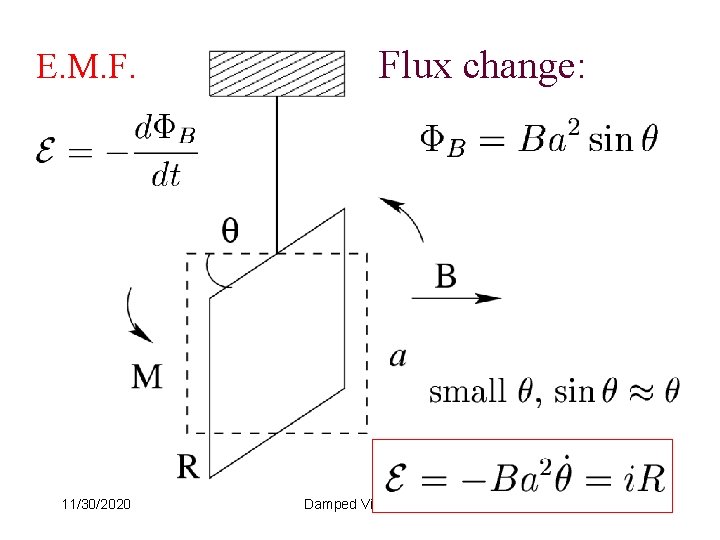
E. M. F. 11/30/2020 Flux change: Damped Vibration

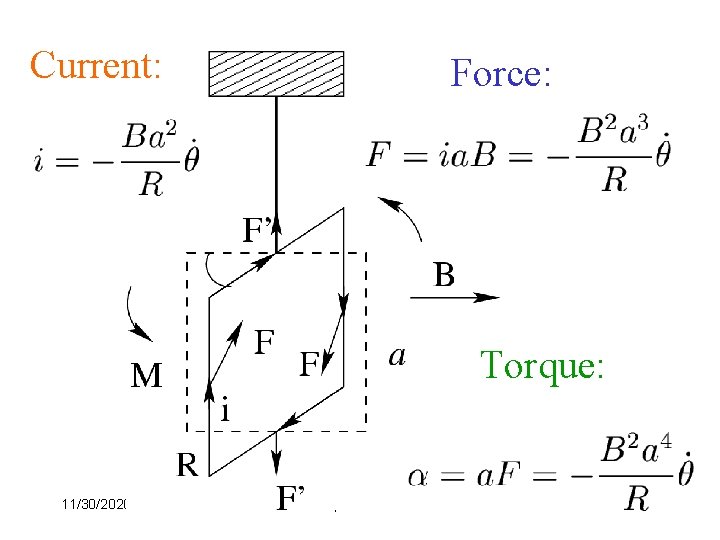
Current: Force: Torque: 11/30/2020 Damped Vibration
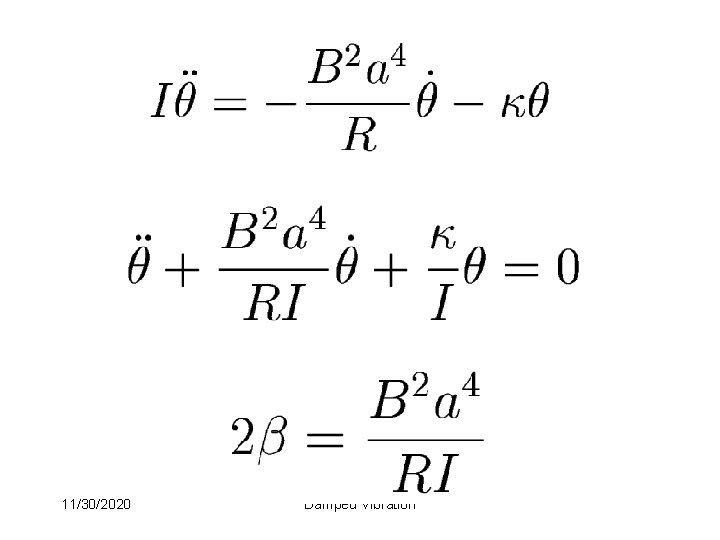
11/30/2020 Damped Vibration

Relaxation time: Moment of inertia: 11/30/2020 Damped Vibration

a problem 11/30/2020 Damped Oscillations 22

Different Initial Conditions Case-2. Impulsed at equilibrium General solution: Underdamped 11/30/2020 Damped Oscillations 23

Situation-2: Overdamped 11/30/2020 Damped Oscillations 24

General solution: Overdamped Case-1. Released from extremity 11/30/2020 Damped Oscillations 25

General solution: Overdamped Case-2. Impulsed at equilibrium 11/30/2020 Damped Oscillations 26

General solution: Overdamped Case-3. position xo : velocity vo 11/30/2020 Damped Oscillations 27

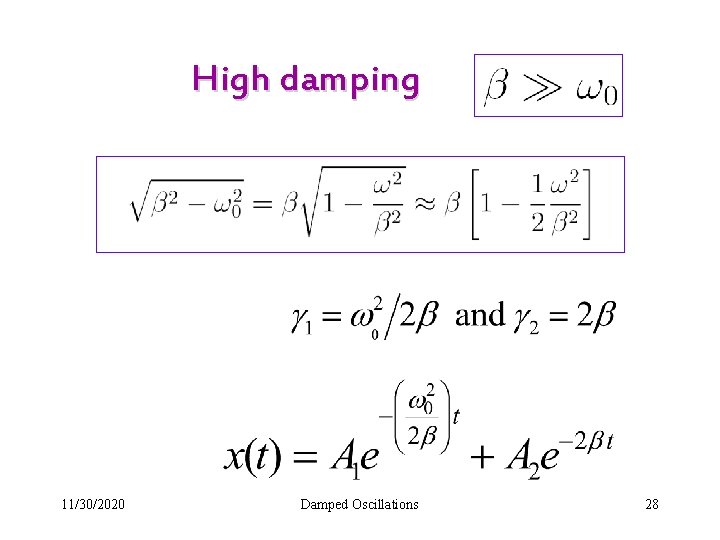
High damping 11/30/2020 Damped Oscillations 28

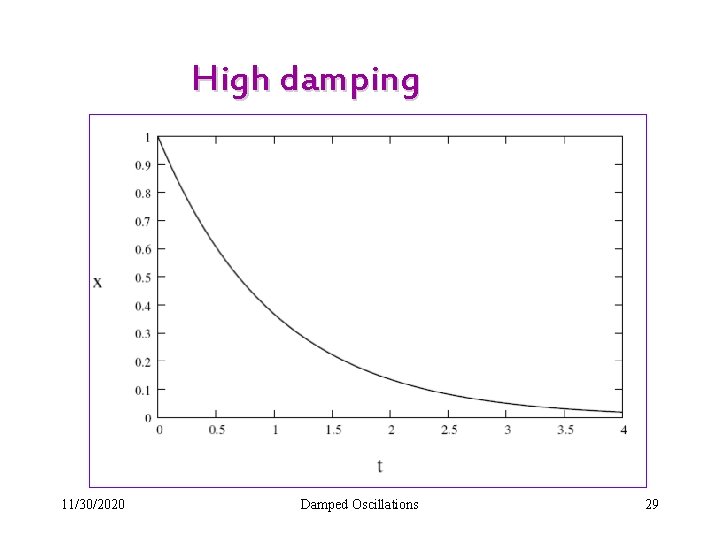
High damping 11/30/2020 Damped Oscillations 29

Situation-3: Critically damped Identical roots General solution 11/30/2020 Damped Oscillations 30

General solution: Critically damped Case-1. Released from extremity 11/30/2020 Damped Oscillations 31

General solution: Critically damped Case-2. Impulsed at equilibrium 11/30/2020 Damped Oscillations 32

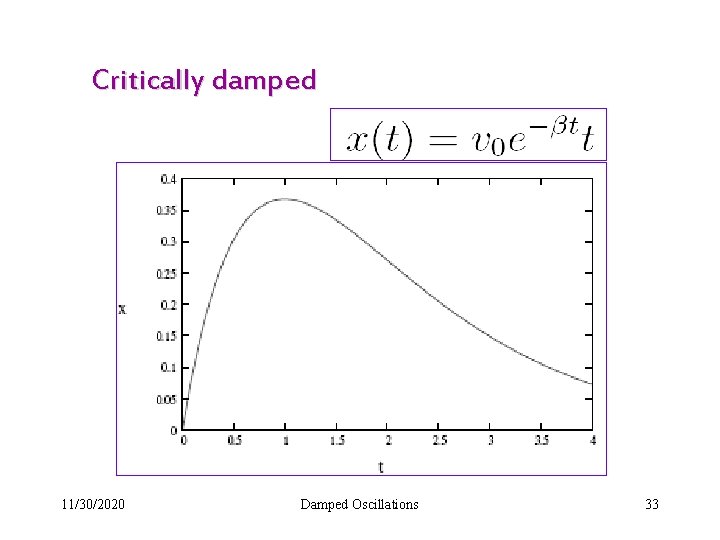
Critically damped 11/30/2020 Damped Oscillations 33

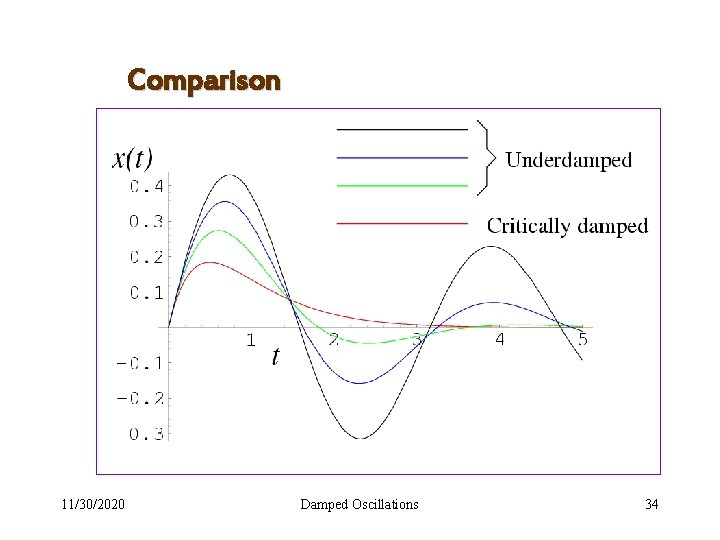
Comparison 11/30/2020 Damped Oscillations 34

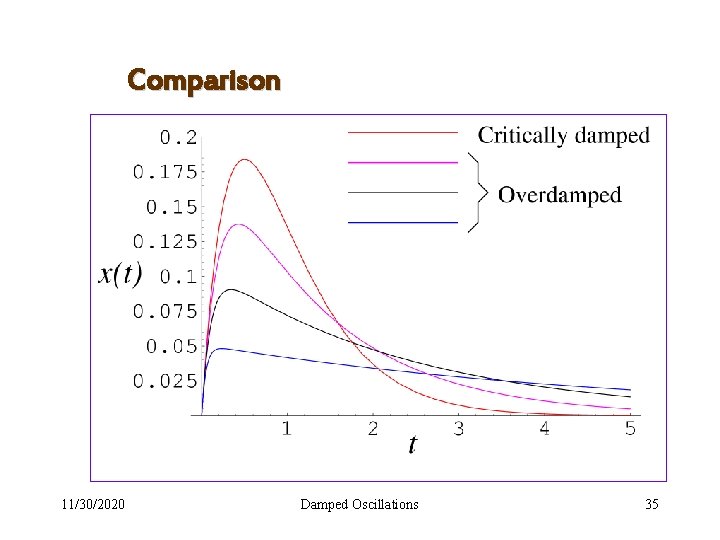
Comparison 11/30/2020 Damped Oscillations 35

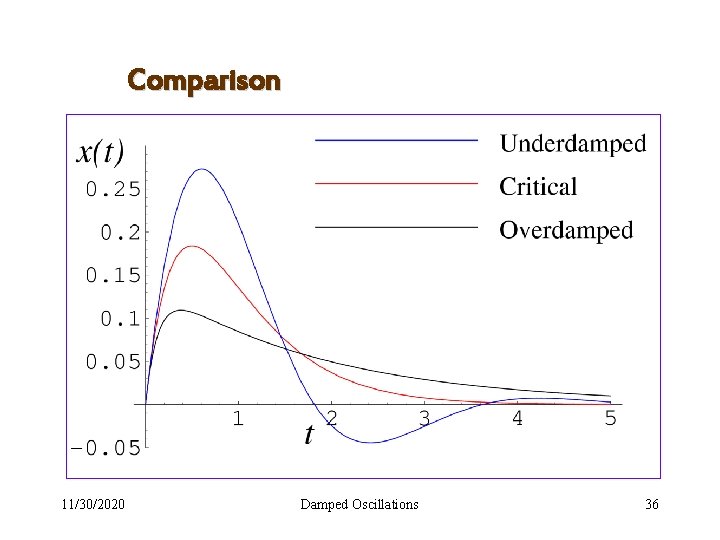
Comparison 11/30/2020 Damped Oscillations 36

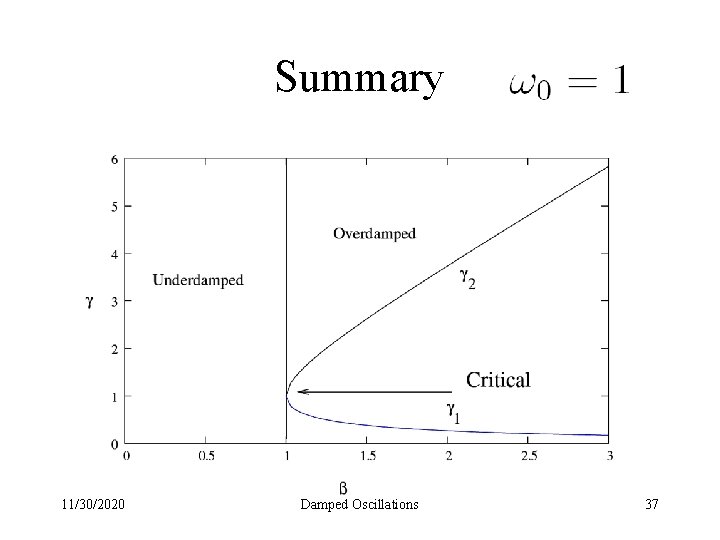
Summary 11/30/2020 Damped Oscillations 37