Dalla felce al fiocco di neve Alla scoperta




































- Slides: 37

Dalla felce al… fiocco di neve! Alla scoperta delle configurazioni nascoste della natura 31/08/2004 A cura di Ivana Niccolai 1

Un frattale IFS: La felce A cura di Ivana Niccolai 2

Osserviamo una felce. . n n Una felce consiste in una serie di fronde, disposte su entrambi i lati di un fusto centrale. La stessa descrizione si applica alle fronde. In molte felci, anche le sottofronde hanno lo stesso tipo di struttura delle fronde e della felce stessa. A cura di Ivana Niccolai 3

Autosimilarità n n n La felce è autosimile, essendo composta di copie di sé stessa in scala ridotta. I matematici idealizzano l’autosimilarità della natura, che è approssimativa, in un’autosimilarità perfetta. La felce è un frattale IFS (Iterated Function System), cioè ottenuto iterando un insieme di trasformazioni del piano. A cura di Ivana Niccolai 4

Idealizzazione dell’autosimilarità della natura n n I matematici studiano le configurazioni naturali costruendo forme ideali, versioni chiare delle strutture naturali, che sono meno regolari. I matematici idealizzano l’autosimilarità della natura, che è approssimativa, in un’autosimilarità perfetta. A cura di Ivana Niccolai 5

La felce del matematico n La felce del matematico ha una struttura dettagliata anche a scale molto più piccole di un atomo e perfino alla scala della più piccola lunghezza significativa dell’universo fisico, vale a dire la lunghezza di Planck (1, 616 * 10 -35 m, all’incirca 10 trilionesimi di metro). A cura di Ivana Niccolai 6

Un frattale IFS: Crystal A cura di Ivana Niccolai 7

Divisione della punta (1/2) n La causa principale delle configurazioni a forma di felce è un fenomeno noto come “divisione della punta”. Certe combinazioni di umidità e temperatura creano condizioni in cui le superfici piane sono dinamicamente instabili. A cura di Ivana Niccolai 8

Divisione della punta (2/2) n Se su una superficie piana si sviluppa una sporgenza, questa cresce più velocemente delle altre regioni. La sporgenza diventa sempre più grande fino a dare origine a una gran quantità di nuove sporgenze più piccole. E’ come un germoglio che si sviluppa , la cui punta si divide ripetutamente in due o più germogli più piccoli (di qui il nome di “divisione della punta”). A cura di Ivana Niccolai 9

Rottura di simmetria n L’intero processo della divisione della punta, può essere visto, con l’occhio del matematico, come una cascata di eventi di rottura di simmetria, che rompono la simmetria traslazionale di una superficie piana. A cura di Ivana Niccolai 10

Dendrite n n Il risultato della rottura di simmetria, nel caso di un cristallo di ghiaccio in formazione, è una configurazione, simile a una felce, nota come dendrite. Il fiocco di neve, quanto meno per alcuni scopi, si può utilmente considerare come un frattale. A cura di Ivana Niccolai 11

Compito della matematica n n Nella scienza, la matematica ha il compito importante di astrarre caratteristiche semplici da un mondo complicato. Analizzandole, si può scoprire la semplicità che sta alla base delle leggi naturali. Per comprendere il fiocco di neve è sensato astrarre le sue caratteristiche semplici. A cura di Ivana Niccolai 12

Modellizzazione matematica n Ai fini di una modellizzazione matematica, possiamo supporre che il fiocco di neve abbia una simmetria esagonale perfetta e che presenti configurazioni di ramificazioni frattali. A cura di Ivana Niccolai 13

Il fiocco di neve e la sua modellizzazione matematica A cura di Ivana Niccolai 14

Confronto tra frattale e fiocco di neve n n Un frattale è un’astrazione matematica; un fiocco di neve è un oggetto reale. Anche i fiocchi di neve hanno quella caratteristica combinazione di ordine e disordine: l’ordine è la simmetria esagonale e il disordine sono le complicate configurazioni ramificate a forma di felce. A cura di Ivana Niccolai 15

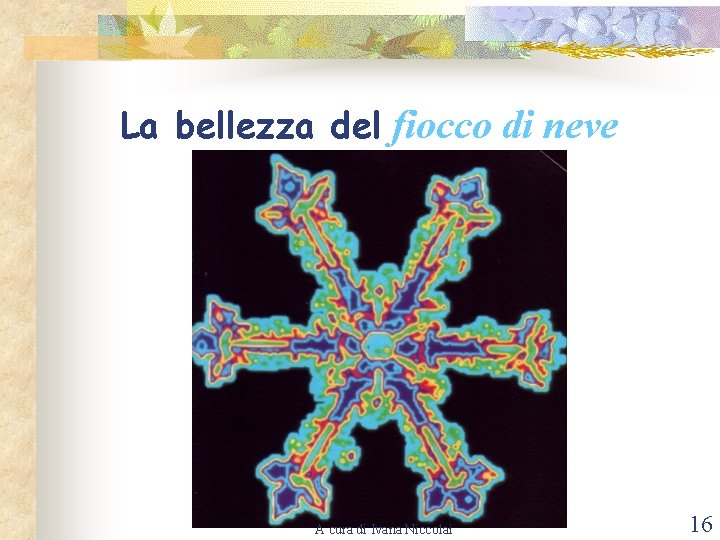
La bellezza del fiocco di neve A cura di Ivana Niccolai 16

Il fascino dei fiocchi di neve n n E’ proprio la combinazione di simmetria e irregolarità a rendere tanto affascinanti i fiocchi di neve. Verso la fine del secolo scorso Martin Golubitsky si rese conto che esiste un modo semplice di combinare simmetria e caos in un unico sistema matematico. A cura di Ivana Niccolai 17

Simmetria e caos n La simmetria e il caos non sono mutuamente esclusivi, ma sono le due facce di una stessa moneta dinamica. Dal punto di vista matematico, la simmetria e il caos possono coesistere e, quando lo fanno, creano bellissimi attrattori simmetrici. A cura di Ivana Niccolai 18

Creazione di configurazioni dendritiche n n Se si scrivono le equazioni dinamiche con la simmetria esagonale del fiocco di neve, scegliendo i coefficienti in modo tale che la dinamica sia caotica, si possono ottenere attrattori caotici con simmetria esagonale. Rimpolpando un po’ le equazioni matematiche , con un caos simmetrico, si possono creare configurazioni dendritiche. A cura di Ivana Niccolai 19

Immagine di attrattori creati con equazioni a simmetria esagonale A cura di Ivana Niccolai 20

Biforcazione n n La parola “catastrofe” non è più di moda; oggi si preferisce usare il termine più neutro “biforcazione”. Se lo stato di un sistema cambia in maniera cospicua per effetto di piccoli cambiamenti esterni, gli scienziati dicono che si è realizzata una biforcazione. A cura di Ivana Niccolai 21

Un particolare tipo di biforcazione n n In natura, la formazione della neve è una biforcazione nello stato di un sistema di molecole d’acqua. La formazione dei fiocchi di neve è legata a un importante tipo di biforcazione: il congelamento. A cura di Ivana Niccolai 22

Transizioni di fase n n n Un piccolo cambiamento di temperatura produce un grosso cambiamento qualitativo nella struttura molecolare e nelle proprietà fisiche dell’acqua. I principali cambiamenti dello stato fisico della materia si chiamano “transizioni di fase”. La cristallizzazione è una transizione di fase. A cura di Ivana Niccolai 23

Fattori che determinano le varie forme dei cristalli di ghiaccio (1/2) Condizioni atmosferiche diverse portano a cristalli di ghiaccio di forme diverse e i fattori più importanti, che determinano tale varietà di forme, sono: n la temperatura; n la sovrassaturazione (che riguarda la quantità di vapore acqueo presente nell’aria), cioè l’umidità disponibile. A cura di Ivana Niccolai 24

Fattori che determinano le varie forme dei cristalli di ghiaccio (2/2) Inoltre: n I valori numerici di questi fattori determinano la forma generale del cristallo; n i dettagli minuti dipendono dalle condizioni caotiche nelle nubi. A cura di Ivana Niccolai 25

Una grande varietà di forme n n I cristalli di ghiaccio presentano una grande varietà di forme. La più semplice, la lamina esagonale, si forma a temperature appena al di sotto del punto di congelamento (tra 0° e – 3°) e a bassi livelli si sovrassaturazione (meno del 30%) A cura di Ivana Niccolai 26

Cristalli dendritici simili a felci (1/2) n Sempre tra 0° e – 3°, ma a livelli più alti di sovrassaturazione (al di sopra del 30%), la simmetria traslazionale di un bordo piatto si rompe e la dinamica va incontro a una biforcazione; le piccole irregolarità vengono amplificate e sul bordo si formano punte e si verifica un processo simile alla divisione della punta, che si ha nei processi di sviluppo frattali. A cura di Ivana Niccolai 27

Cristalli dendritici simili a felci (2/2) n La regolarità geometrica del reticolo cristallino fa sì che questo processo di sviluppo frattale generi cristalli dendritici simili a felci. A cura di Ivana Niccolai 28

Presentazione di alcune forme dei cristalli di neve (1/2) n n n Intorno al livello di sovrassaturazione del 30%, si trovano molte altre forme di cristalli di ghiaccio, a seconda della temperatura. Tra – 3° e – 5° i cristalli sono a forma di aghi Tra – 5° e – 8° il ghiaccio forma prismi esagonali cavi A cura di Ivana Niccolai 29

Presentazione di alcune forme dei cristalli di neve (2/2) n n Tra – 8° e – 12° e di nuovo tra – 16° e – 24° si osservano sottili lamine con decorazioni simmetriche Tra – 12° e – 16° ricompaiono i cristalli dendritici e, a temperature più basse (- 24°) ricompaiono i prismi cavi. A cura di Ivana Niccolai 30

Affermazione di Jan Stewart n Ian Stewart, professore di matematica all’Università di Warwick, in Gran Bretagna, nel suo libro “Che forma ha un fiocco di neve? ”, Bollati Boringhieri Editore, ha affermato: “Laddove il bambino vedeva una felce su una finestra ghiacciata, oggi l’adulto vede lo sviluppo frattale di molecole cristalline e la simmetria nascosta delle forze della natura”. A cura di Ivana Niccolai 31

Il fiocco di neve di Koch è un frattale L-SYSTEM A cura di Ivana Niccolai 32

L-SYSTEM (Lindenmayer-System) n Lindenmayer è il nome del biologo olandese che nel 1968 inventò una formalizzazione (L-SYSTEM) della descrizione del processo di generazione dei rami delle piante, adatta per essere implementata con programmi di computer graphics. A cura di Ivana Niccolai 33

Costruzione del fiocco di neve di Koch 1/2 n Si parte da un triangolo equilatero e si incolla un triangolo più piccolo, di lato pari a 1/3 del lato originario, sul segmento centrale di ogni lato, ottenendo una stella a sei punte. A cura di Ivana Niccolai 34

Costruzione del fiocco di neve di Koch 2/2 n Si ripete, poi, la procedura con altri 12 triangoli, di lato pari a 1/9 del lato originario, poi con altri 48 triangoli di lato pari a 1/27 del lato originario e così via… A cura di Ivana Niccolai 35

Perimetro infinito del fiocco di neve di Koch n La forma del fiocco di neve di Kock ha un perimetro infinito (ogni stadio della costruzione ne moltiplica la lunghezza per 4/3) A cura di Ivana Niccolai 36

Il fiocco di neve di Koch assomiglia a un fiocco di neve vero? n Il fiocco di neve, inventato alla fine del secolo XIX dal matematico svedese Helge von Koch, è troppo regolare, per assomigliare a un fiocco di neve vero, ciò nonostante coglie alcune caratteristiche della sua forma ad albero, perché tali caratteristiche fanno ricordare ai matematici la simmetria esagonale e le configurazioni di ramificazioni frattali. A cura di Ivana Niccolai 37
 Chimica più posca fiorani soluzioni
Chimica più posca fiorani soluzioni Elementi di geometria analitica
Elementi di geometria analitica Posca soluzioni
Posca soluzioni Chimica più verde soluzioni
Chimica più verde soluzioni Dalla monarchia alla repubblica romana
Dalla monarchia alla repubblica romana Soluzioni capitolo 14 chimica
Soluzioni capitolo 14 chimica Passaggio dalla preistoria alla storia
Passaggio dalla preistoria alla storia Forma attiva e passiva esercizi
Forma attiva e passiva esercizi Molecole in movimento soluzioni capitolo 14
Molecole in movimento soluzioni capitolo 14 Dalla monarchia alla repubblica romana
Dalla monarchia alla repubblica romana Passaggio dalla preistoria alla storia
Passaggio dalla preistoria alla storia Banderita tu eres roja letra
Banderita tu eres roja letra Para que mi amor no sea un sentimiento letra
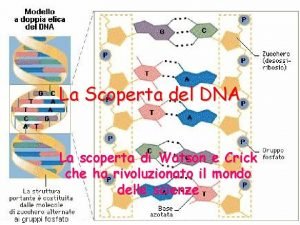
Para que mi amor no sea un sentimiento letra Scoperta dna 1869
Scoperta dna 1869 Apprendimento per scoperta dewey
Apprendimento per scoperta dewey Hooke scientist cell theory
Hooke scientist cell theory Scoperta neutrone
Scoperta neutrone Brunee gusto e passione
Brunee gusto e passione Apprendimento significativo ausubel
Apprendimento significativo ausubel Alessandra spreafico
Alessandra spreafico Affluenti del po scuola primaria
Affluenti del po scuola primaria Particolarità della prima declinazione
Particolarità della prima declinazione Előbél szakaszai
Előbél szakaszai Qti authoring tool
Qti authoring tool La neve e soffice
La neve e soffice Hilary neve
Hilary neve Leia as frases 1 e 2 e, a seguir, marque a resposta correta
Leia as frases 1 e 2 e, a seguir, marque a resposta correta Sárgarigó népies neve
Sárgarigó népies neve Branca de neve brincando com os troféus do pai
Branca de neve brincando com os troféus do pai Középnehéz elemi részecskék összefoglaló neve
Középnehéz elemi részecskék összefoglaló neve Egri csillagok bornemissza gergely tulajdonságai
Egri csillagok bornemissza gergely tulajdonságai Sirály rendszertani neve
Sirály rendszertani neve Szerves csoport
Szerves csoport Declinazione mare maris
Declinazione mare maris Esempio piano di manutenzione delle strutture ntc 2018 doc
Esempio piano di manutenzione delle strutture ntc 2018 doc Me lo rimandi
Me lo rimandi Le 10 cose che ho imparato dalla vita
Le 10 cose che ho imparato dalla vita Fuga dalla tv
Fuga dalla tv