Dal MODELLO ICF dellOMS alla PROGETTAZIONE nella SCUOLA

Dal MODELLO ICF dell’OMS alla PROGETTAZIONE nella SCUOLA. «IL MODELLO ICF PER L’INCLUSIONE» Prof. ssa Marialetizia Pedrinazzi

Dalla Diagnosi Funzionale dell’alunno X…. codice b 1646. 2 definizione Soluzione di problemi Funzioni mentali dell'identificare, analizzare e interagire in una soluzione descrizione delle informazioni incongruenti o in conflitto. Nota : nella classificazione ICF la lettera b individua le funzioni corporee ossia gli aspetti cognitivi in cui emergono delle carenze, cioè delle menomazioni, riscontrate dalla Neuropsichiatria nella diagnosi funzionale. Prof. ssa Marialetizia Pedrinazzi

Dalla Diagnosi Funzionale dell’alunno X…. codice b 172. 2 definizione Funzioni di calcolo Funzioni mentali specifiche di determinazione, approssimazione e descrizione utilizzo di simboli e processi matematici. Funzioni di addizione, sottrazione e altri inclusione semplici calcoli matematici; funzioni di complesse operazioni matematiche. Prof. ssa Marialetizia Pedrinazzi

L’alunno X evidenzia difficoltà…. . codice d 150. 2 definizione Imparare a calcolare Sviluppare la capacità di usare i numeri ed eseguire operazioni matematiche semplici e complesse, come usare simboli matematici descrizione per l'addizione e la sottrazione e applicare a un problema l'operazione matematica corretta. Prof. ssa Marialetizia Pedrinazzi

L’alunno X evidenzia difficoltà…. . codice d 1371. 3 definizione Acquisire concetti complessi Imparare a usare concetti come quelli descrizione di classificazione, raggruppamento, reversibilità, seriazione. Nota : nella classificazione ICF la lettera d individua le attività in cui si manifestano difficoltà. Prof. ssa Marialetizia Pedrinazzi

Obiettivi degli insegnanti curriculari e di sostegno Codice d 150. 2 Codice d 150. 1 Codice d 1371. 3 Codice d 1371. 2 Prof. ssa Marialetizia Pedrinazzi

Ruolo degli insegnanti curriculari e di sostegno codice e 330+2 definizione Persone in posizioni di autorità Individui che hanno responsabilità di prendere decisioni per altri e che esercitano un'influenza o un potere socialmente definito sulla base del loro ruolo sociale, economico, culturale o descrizione religioso nella società, come insegnanti CURRICOLARI e di SOSTEGNO, datori di lavoro, supervisori, capi religiosi, viceresponsabili, guardiani o amministratori. Prof. ssa Marialetizia Pedrinazzi

Studio domestico codice e 340+1 definizione Persone che forniscono aiuto o assistenza descrizione Individui che forniscono i servizi richiesti per aiutare le persone nelle loro attività quotidiane, nel sostentamento o nell'esecuzione di compiti al lavoro, nell'istruzione o in altre situazioni di vita, finanziati sia con fondi pubblici che privati, o anche su base volontaria, come assistenti domiciliari, DOCENTI PER LO STUDIO POMERIDIANO A CASA, CASA assistenti ad personam, assistenti per il trasporto, aiuto a pagamento, bambinaie e altri assistenti che hanno la funzione di carer principali. Prof. ssa Marialetizia Pedrinazzi

La scuola dell’integrazione/inclusione è la scuola del superamento delle differenze individuali, individuali grazie alla loro valorizzazione, valorizzazione del protagonismo degli alunni, dell’ascolto e del rispetto del reciproco. E’ fondamentale creare le condizioni affinché l’alunno X possa frequentare positivamente la stessa classe dei suoi coetanei. Prof. ssa Marialetizia Pedrinazzi

Come i Docenti Curriculari e di Sostegno possono agire da FACILITATORI ? Il lavoro di sostegno avviene essenzialmente in classe. Lezioni frontali/dialogate per ciò che riguarda la parte teorica con l’esposizione dei contenuti fondamentali da parte dell’insegnante curriculare L’insegnante di sostegno segue alunno X nello svolgimento degli esercizi e nella correzione di quelli assegnati per casa, stimolandone la partecipazione attiva all’attività didattica. Prof. ssa Marialetizia Pedrinazzi

Come i Docenti Curriculari e di Sostegno possono agire da FACILITATORI ? Ogni lezione, il docente curriculare riprende il lavoro svolto nella precedente attraverso domande specifiche al fine di esercitare l’allievo X all’esposizione orale e mirate al consolidamento delle conoscenze. Prepara schematizzazioni dei singoli argomenti e concetti, mappe concettuali per rendere più agevole l’apprendimento. Prof. ssa Marialetizia Pedrinazzi

Come i Docenti Curriculari e di Sostegno possono agire da FACILITATORI ? Oltre al libro di testo si utilizzano altri strumenti che facilitino e semplifichino la comprensione dei concetti : appunti, schemi e fotocopie di altri testi, ecc. Dopo la lezione conclusiva di un argomento/modulo l’alunno X può rivedere e rielaborare le nozioni utilizzando opportuni materiali preparati dal docente curriculare e/o sostegno. Prof. ssa Marialetizia Pedrinazzi

Un Esempio…. . Le espressioni Il docente curriculare e/o il docente di sostegno facilitano l’apprendimento delle tecniche di risoluzione delle espressioni numeriche con schemi ed esercizi guidati. Prof. ssa Marialetizia Pedrinazzi

Un Esempio…. . Le espressioni Rivedi e studia il seguente schema ……. . e poi risolvi le seguenti espressioni, seguendo le indicazioni…… Prof. ssa Marialetizia Pedrinazzi

Un‘espressione può essere : Senza parentesi Con parentesi Per risolverla : Prima si eseguono le moltiplicazioni e le divisioni nell’ordine in cui sono indicate. Poi si eseguono le addizioni e le sottrazioni, sempre nell’ordine in cui sono indicate. Prof. ssa Marialetizia Pedrinazzi Prima si eseguono le operazioni che compaiono nelle parentesi tonde. Poi si eseguono le operazioni che compaiono nelle parentesi quadre. Infine si eseguono le operazioni che compaiono nelle parentesi graffe.

Calcola il valore della seguente espressione , seguendo le indicazioni 24 : 2 + 22 – 3 · 2 = Nell’espressione le operazioni proposte in ordine sono le seguenti: divisione, somma, elevamento a potenza, sottrazione e moltiplicazione. Poiché la successione risulta errata per il calcolo corretto dell’espressione, ricostruisci la sequenza esatta………… 24 : 2 + 22 – 3 · 2 = Ora esegui……………… Prof. ssa Marialetizia Pedrinazzi

Calcola il valore della seguente espressione , seguendo le indicazioni 3 · 5 + [16 – (4 + 2 · 3)] + 16 : 8 – 1 = Risolvi le operazioni indicate tra la parentesi tonda …………………. . Risolvi le operazioni indicate tra la parentesi quadra …………………. . . Esegui la moltiplicazione e la divisione nell’ordine di scrittura……………. E poi le addizioni e la sottrazione……………. . . Il risultato ottenuto è …………. Prof. ssa Marialetizia Pedrinazzi

Un Esempio…. . Le equazioni Il docente curriculare e/o il docente di sostegno facilitano con schemi ed esercizi guidati l’apprendimento del concetto di equazione e delle relative procedure di risoluzione, partendo da un semplice problemino tratto dalla vita reale. Prof. ssa Marialetizia Pedrinazzi

LE EQUAZIONI Partiamo da un problemino……. Prof. ssa Marialetizia Pedrinazzi Sono andato dal panettiere con 10 euro e ho comprato due pizzette. Esco con 6 euro: quanto costa una pizzetta?

Risolviamo insieme il problema usando il linguaggio matematico……. Indichiamo con x il prezzo che non conosciamo e che vogliamo determinare: Sono andato dal panettiere con 10 euro 10 ho comprato due pizzette -2 x Esco con 6 euro: quanto costa una pizzetta? = 6 Prof. ssa Marialetizia Pedrinazzi

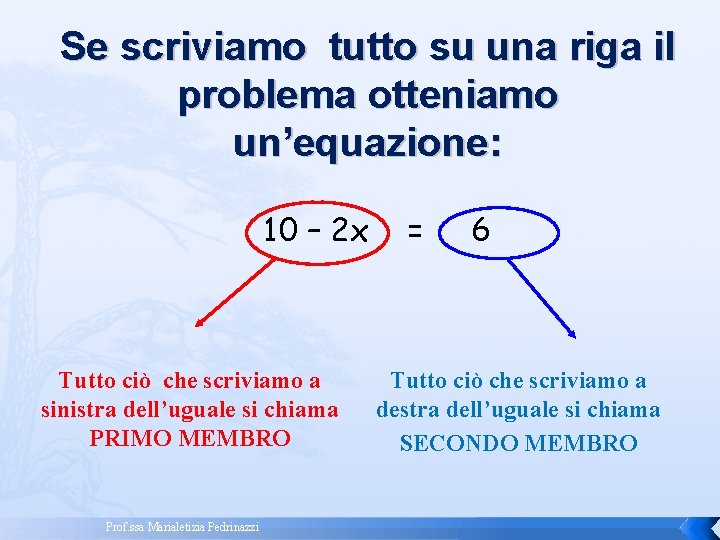
Se scriviamo tutto su una riga il problema otteniamo un’equazione: 10 – 2 x Tutto ciò che scriviamo a sinistra dell’uguale si chiama PRIMO MEMBRO Prof. ssa Marialetizia Pedrinazzi = 6 Tutto ciò che scriviamo a destra dell’uguale si chiama SECONDO MEMBRO

Seguono ………… Risoluzione dell’equazione, proposta dal docente curriculare Schemi sui principi di equivalenza e sulle procedure di risoluzione Numerosi esempi………. . Prof. ssa Marialetizia Pedrinazzi

Le equazioni. Ora lavora lo studente …. . . Adesso prova tu……. . Rivedi e studia appunti e schemi, poi risolvi la seguente equazione, seguendo le indicazioni…… Prof. ssa Marialetizia Pedrinazzi

Porta al primo membro tutti i termini con l’incognita x e al secondo membro tutti i numeri. Per eliminare ………. al primo membro bisogna …………………. ai due membri dell’equazione: …………………. = ………………. . ……………… Ottieni: ……………………………. . Per eliminare ……. . al secondo membro bisogna …………………. . ai due membri dell’equazione: …………………. = ……………… Il risultato è ………………. . Prof. ssa Marialetizia Pedrinazzi

Gli esempi proposti prendono spunto dai numerosi materiali predisposti dai docenti del Dipartimento di Sostegno e di Matematica dell’Istituto Pesenti per facilitare l’attività didattica in classe ed il lavoro domestico. Prof. ssa Marialetizia Pedrinazzi