Cyclic and Bicyclic Decompositions of the Complete Graph

Cyclic and Bicyclic Decompositions of the Complete Graph into the 4 -Cycle with a Pendant Edge Daniel “Lupo” Cantrell Gary “Hoser” Coker Robert “Knob” Gardner* *Presenter, East Tennessee State University, Department of Mathematics and Statistics 2010 Southeastern MAA Conference Elon University; Elon, NC March 26, 2010

Act 1. Decompositions Steiner Triple Systems Jakob Steiner 1850 s

Definition. A decomposition of a simple graph H with isomorphic copies of graph G is a set { G 1, G 2, … , Gn} where Gi G and V(Gi) V(H) for all i, E(Gi) ∩ E(Gj) = Ø if i ≠ j, and Gi = H.
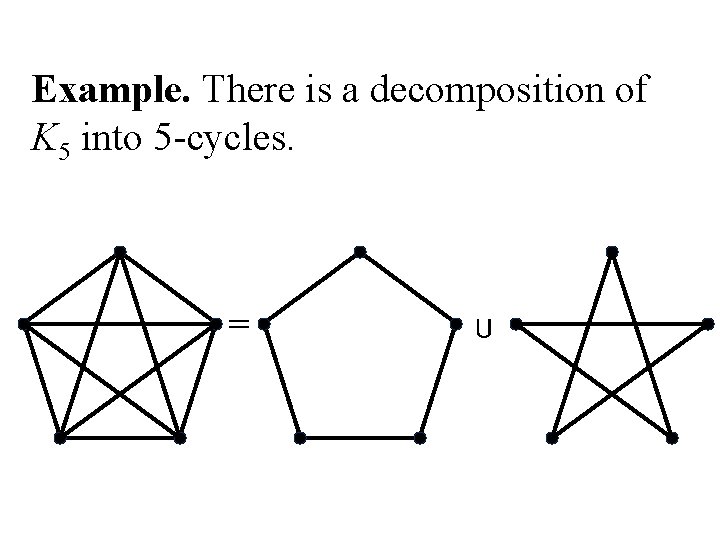
Example. There is a decomposition of K 5 into 5 -cycles. = U
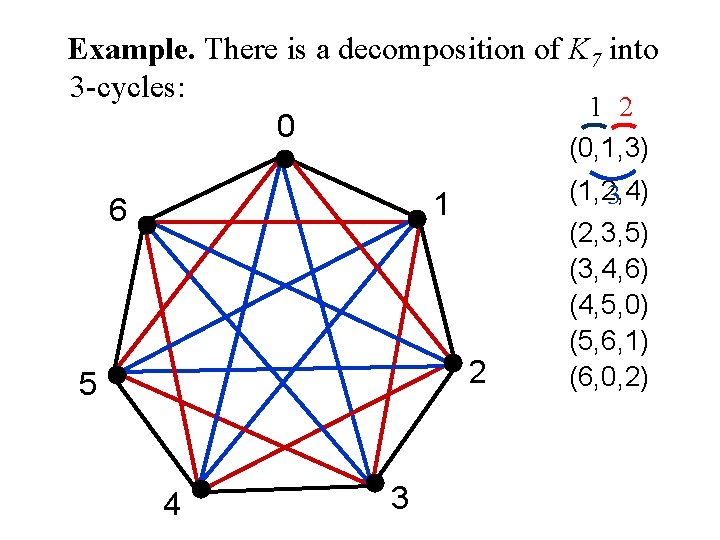
Example. There is a decomposition of K 7 into 3 -cycles: 1 2 0 (0, 1, 3) 1 6 2 5 4 3 (1, 2, 4) 3 (2, 3, 5) (3, 4, 6) (4, 5, 0) (5, 6, 1) (6, 0, 2)

Note. We shall restrict today’s presentation to decompositions of complete graphs. Definition. A Steiner triple system of order v, STS(v), is a decomposition of the complete graph on v vertices, Kv , into 3 -cycles.

Jakob Steiner 1796 -1863 v ≡ 1 or 3 (mod 6) is necessary. From the Saint Andrews Mac. Tutor History of Mathematics website. J. Steiner, Combinatorische Aufgabe, Journal für die Reine und angewandte Mathematik (Crelle’s Journal), 45 (1853), 181 -182.

Theorem. A STS(v) exists if and only if v ≡ 1 or 3 (mod 6). Note. Sufficiency follows from Reiss. M. Reiss, Über eine Steinersche combinatorsche Aufgabe welche in 45 sten Bande dieses Journals, Seite 181, gestellt worden ist, Journal für die Reine und angewandte Mathematik (Crelle’s Journal), 56 (1859), 326 -344.

Thomas P. Kirkman 1806 -1895 STS(v) iff v ≡ 1 or 3 (mod 6). From the Saint Andrews Mac. Tutor History of Mathematics website. T. Kirkman, On a problem in combinations, Cambridge and Dublin Mathematics Journal, 2 (1847), 191 -204.
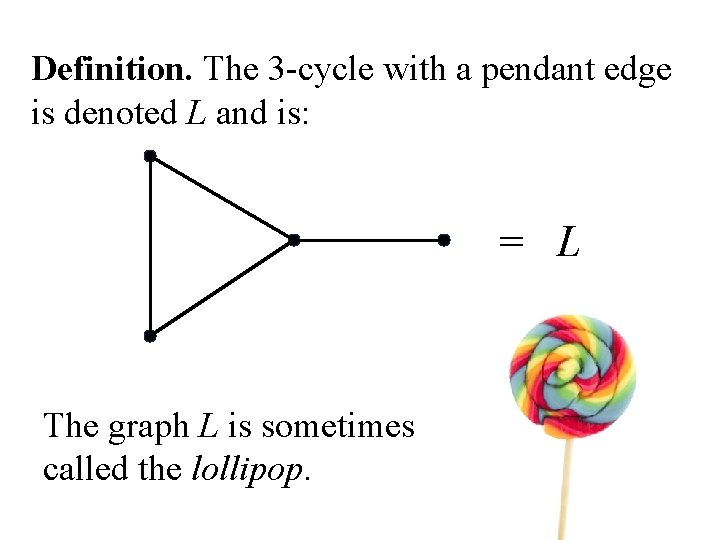
Definition. The 3 -cycle with a pendant edge is denoted L and is: = L The graph L is sometimes called the lollipop.

Theorem. An L-decomposition of Kv exists if and only if v ≡ 0 or 1 (mod 8). Jean-Claude Bermond From Bermond’s website: http: //wwwsop. inria. fr/members/Jean-Claude. Bermond/ J. C. Bermond and J. Schonheim, G-Decompositions of Kn where G has Four Vertices or Less, Discrete Math. 19 (1977), 113 -120.
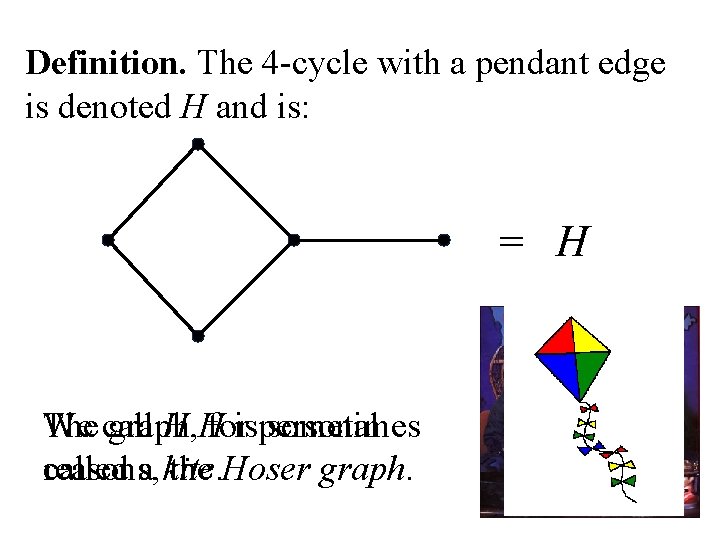
Definition. The 4 -cycle with a pendant edge is denoted H and is: = H We call The graph H, H forispersonal sometimes called a kite. reasons, the Hoser graph.

Theorem. An H-decomposition of Kv exists if and only if v ≡ 0 or 1 (mod 5) and v ≥ 11. Alex Rosa Dominique Sotteau From: http: //www. d. umn. edu/~dfroncek/alex/ and http: //wwwdirection. inria. fr/international/DS/page_personnelle. html J. C. Bermond, C. Huang, A. Rosa, and D. Sotteau, Decompositions of Complete Graphs into Isomorphic Subgraphs with Five Vertices, Ars Combinatoria 10 (1980), 211 -254.

Act 2. Automorphisms, eh! Take off! Cycles and Bicycles Peltesohn and Gardner 1930 s to present

Definition. An automorphism of a Gdecomposition of H is a permutation of V(H) which fixes the set of copies of G, { G 1, G 2, … , Gn}. Recall. A permutation can be classified by its disjoint decomposition into cycles.
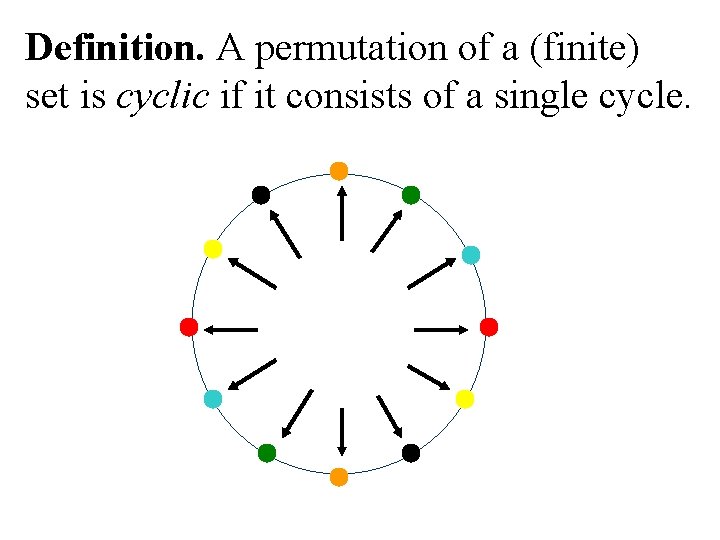
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
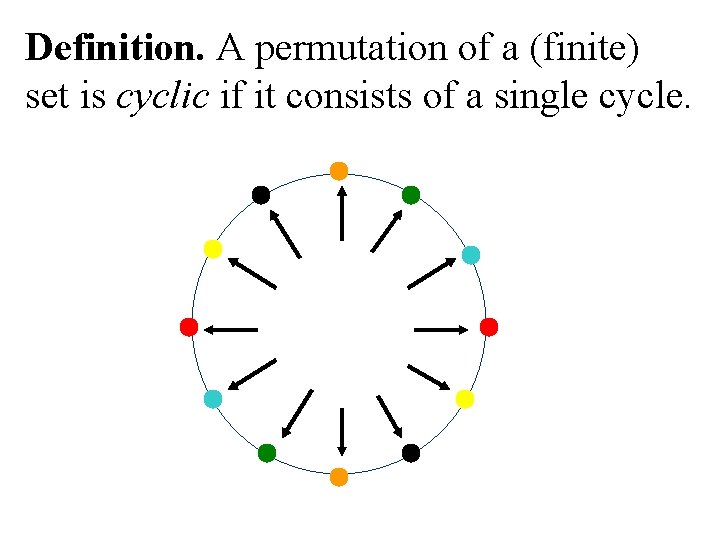
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
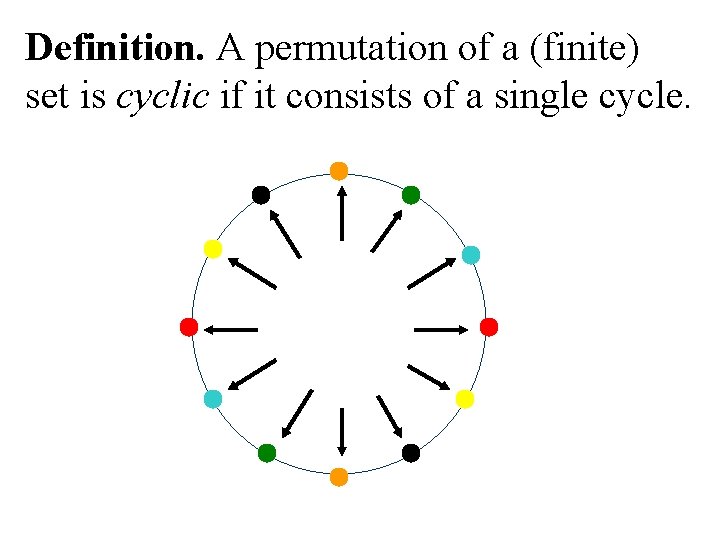
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
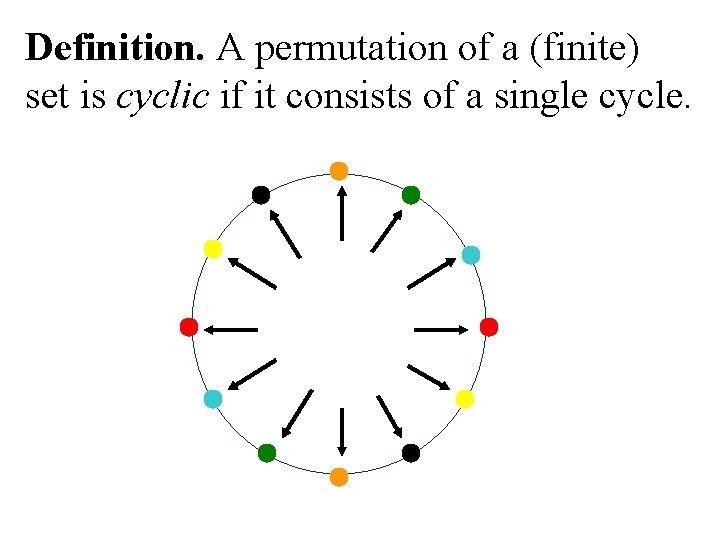
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
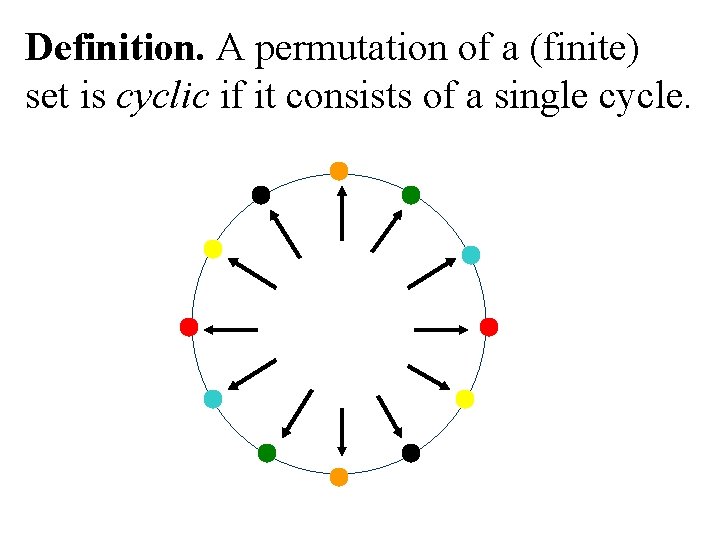
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
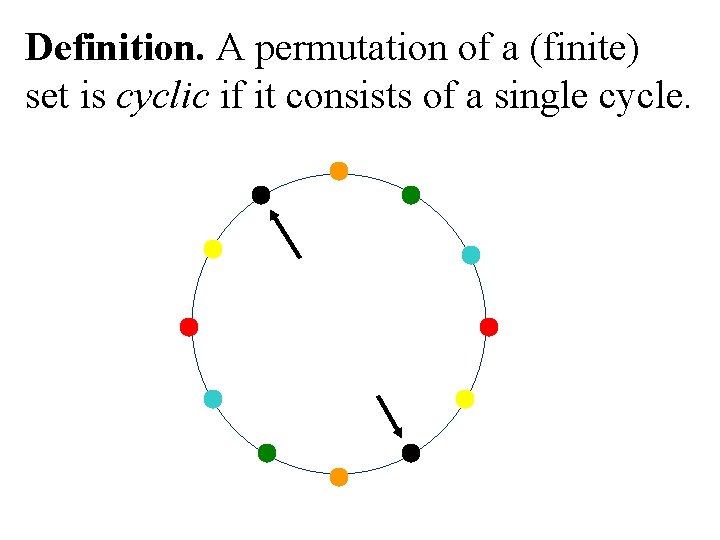
Definition. A permutation of a (finite) set is cyclic if it consists of a single cycle.
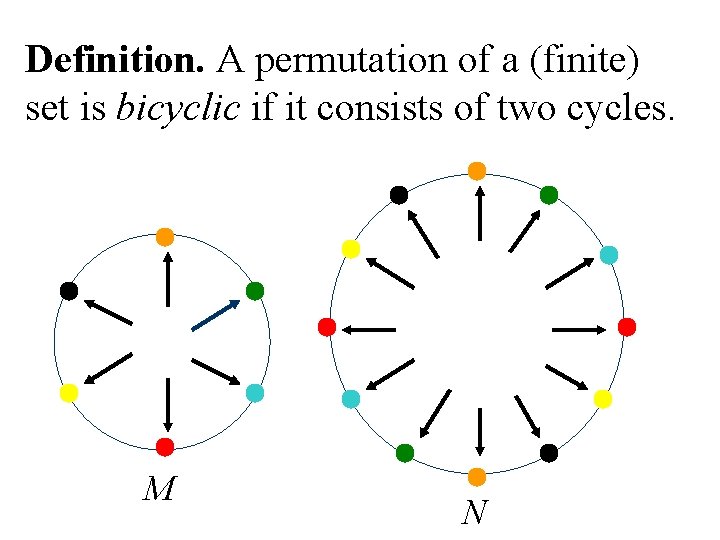
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N
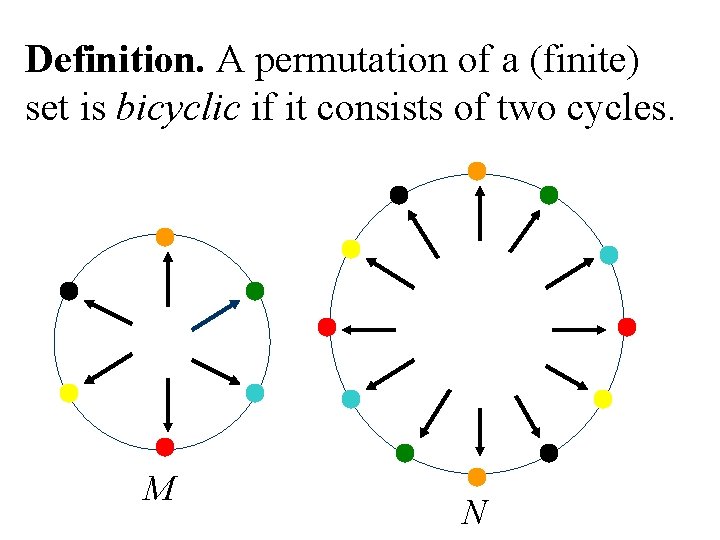
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N
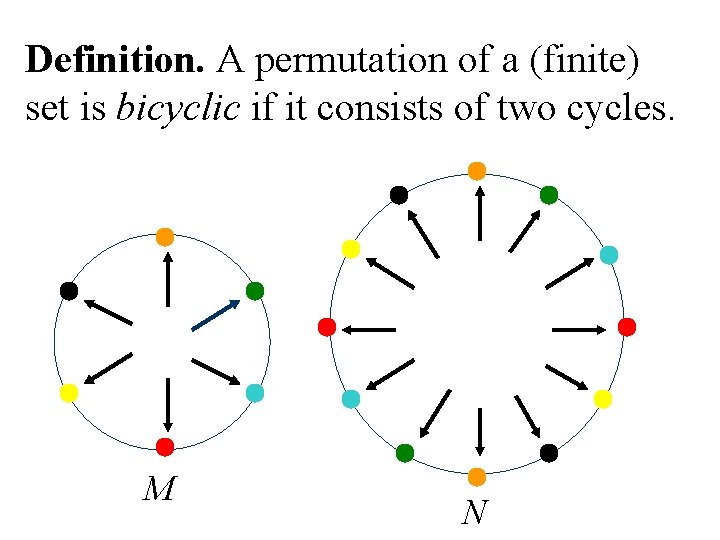
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N
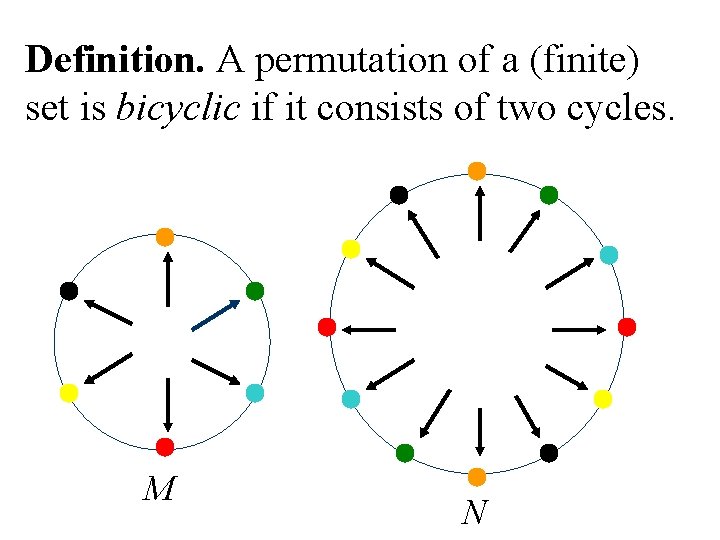
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N
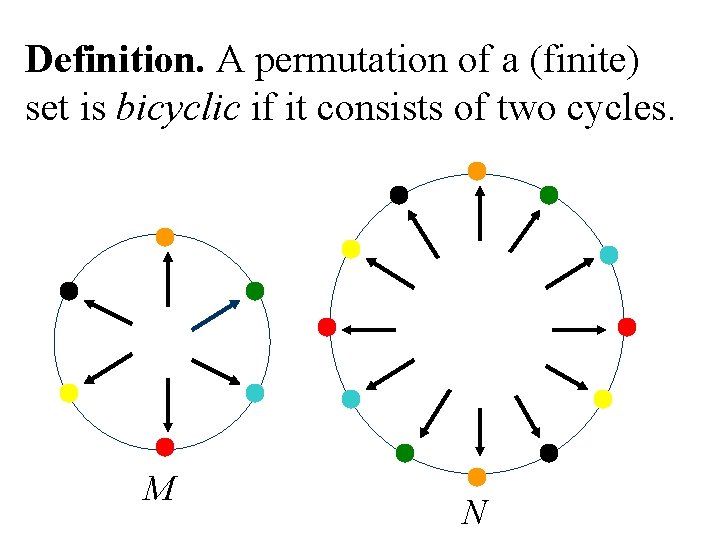
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N
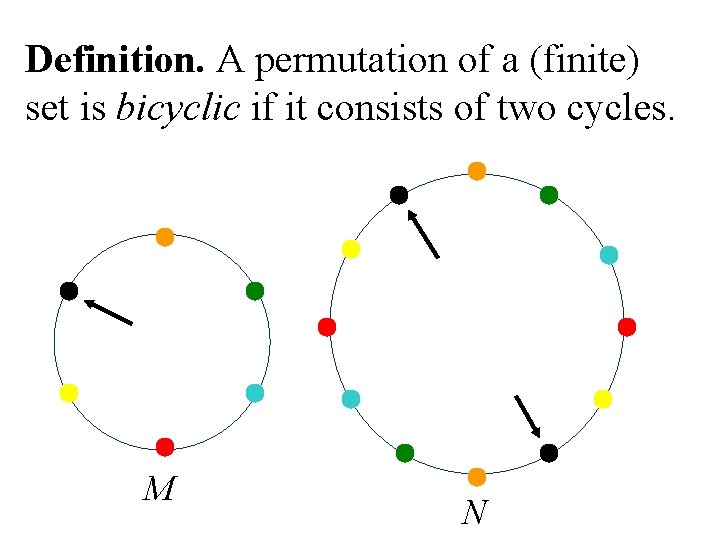
Definition. A permutation of a (finite) set is bicyclic if it consists of two cycles. M N

Theorem. A STS(v) admitting a cyclic automorphism exists if and only if v ≡ 1 or 3 (mod 6), v ≠ 9. R. Peltesohn, A Solution to Both of Heffter's Difference Problems (in German), Compositio Math. 6 (1939), 251257.

Theorem. A bicyclic Steiner Triple System of order v exists if and only if v = M + N ≡ 1 or 3 (mod 6), M ≠ 9 (M > 1), and M | N. R. Calahan and R. Gardner, Bicyclic Steiner Triple Systems, Discrete Math. 128 (1994), 35 -44.

Theorem. A cyclic L-decomposition of Kv exists if and only if v ≡ 1 (mod 8). J. C. Bermond and J. Schonheim, G-Decompositions of Kn where G has Four Vertices or Less, Discrete Math. 19 (1977), 113 -120. R. Gardner, Bicyclic Decompositions of Kv into Copies of K 3 {e}, Utilitas Mathematica 54 (1998), 51 -57.

Theorem. A bicyclic L-decomposition of Kv exists if and only if (i) N = 2 M and v = M + N ≡ 9 (mod 24), or (ii) M ≡ 1 (mod 8) and N = k M where k ≡ 7 (mod 8). R. Gardner, Bicyclic Decompositions of Kv into Copies of K 3 {e}, Utilitas Mathematica 54 (1998), 51 -57.

Act 3. New Results Hoser Graphs Cantrell, Coker, Gardner 2010

Theorem. A cyclic H-decomposition of Kv exists if and only if v ≡ 1 (mod 10). D. Cantrell, G. D. Coker, and R. Gardner, Cyclic, f-Cyclic, and Bicyclic Decompositions of the Complete Graph into the 4 -Cycle with a Pendant Edge, Utilitas Mathematica, to appear.
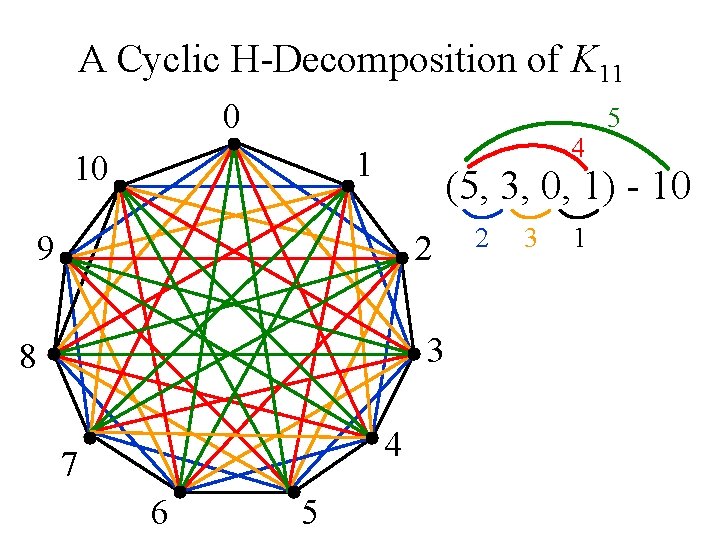
A Cyclic H-Decomposition of K 11 0 4 1 10 (5, 3, 0, 1) - 10 9 2 3 8 4 7 6 5 5 2 3 1

Theorem. A bicyclic H-decomposition of Kv, exists if and only if (i) M = N ≡ 3 (mod 10), M = N ≥ 13, or (ii) M ≡ 1 (mod 10) and N = k M where k ≡ 9 (mod 10). D. Cantrell, G. D. Coker, and R. Gardner, Cyclic, f-Cyclic, and Bicyclic Decompositions of the Complete Graph into the 4 -Cycle with a Pendant Edge, Utilitas Mathematica, to appear.

A Bicyclic H-decomposition of K 26 With M = N = 13.

Special Thanks To: Elsinore Beer for the inspiration for this research!

Good Day, eh!
- Slides: 38