Cyber Intrusion Detection Algorithm Based on Bayes Theorem

Cyber Intrusion Detection Algorithm Based on Bayes’ Theorem Stephanie Steren-Ruta- West High School ‘ 12 Syeda Faiza Islam- Farragut High School ‘ 15 Young Scholars Program July 17, 2012 Knoxville, Tennessee

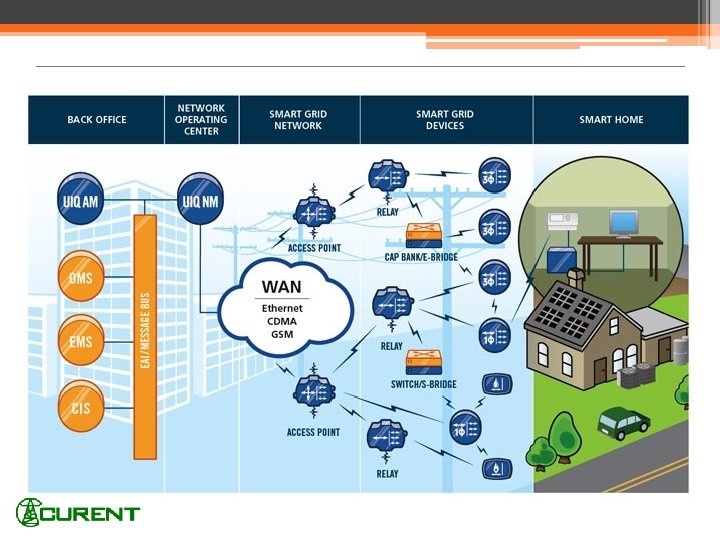
The problem • Securing the Smart Grid ▫ Effective ways

06 -3 • http: //www. youtube. com/watch? v=P 0 xf. Rh. M 1 J p 8

Terms • Intrusion Detection • Pattern recognition • Bayes Theorem • Maximum a-posterior probability (MAP)

Intrusion Detection • identify unauthorized use, misuse and abuse of computer systems by both system insiders and external predators.

Types of Intrusions • Denial of Service (DOS) • Remote to Local (R 2 L) • User to Root (U 2 R) • Probing

06 -7 Pattern Recognition • identifying the patterns in a set of data and classifying and categorizing it

Bayes' Theorem • is a mathematical formula used for calculating conditional probabilities

Maximum a-posterior probability (MAP) • Assigning to the sample of interest the membership based on which the sample has the highest a-posterior probability.

Bayes' Theorem •

Multivariate Gaussian Distribution •

Discriminant Function •

Analysis of Data • Have a training data and testing data that have results. • Take the training and separate into the different categories • Acquire the covariance and mean • Make a loop that tests all categories with the discriminant function • Check for accuracy • Change prior-probability until acquiring most accurate result

06 -14 Data Set

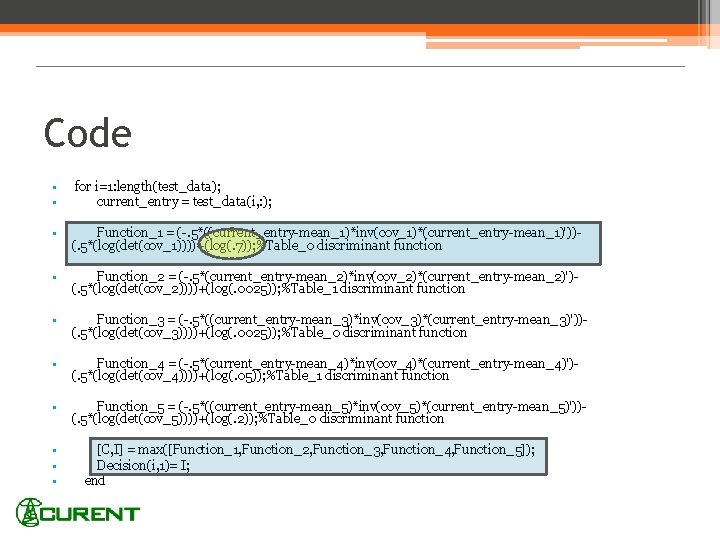
Code • • for i=1: length(test_data); current_entry = test_data(i, : ); • Function_1 = (-. 5*((current_entry-mean_1)*inv(cov_1)*(current_entry-mean_1)'))(. 5*(log(det(cov_1))))+(log(. 7)); %Table_0 discriminant function • Function_2 = (-. 5*(current_entry-mean_2)*inv(cov_2)*(current_entry-mean_2)')(. 5*(log(det(cov_2))))+(log(. 0025)); %Table_1 discriminant function • Function_3 = (-. 5*((current_entry-mean_3)*inv(cov_3)*(current_entry-mean_3)'))(. 5*(log(det(cov_3))))+(log(. 0025)); %Table_0 discriminant function • Function_4 = (-. 5*(current_entry-mean_4)*inv(cov_4)*(current_entry-mean_4)')(. 5*(log(det(cov_4))))+(log(. 05)); %Table_1 discriminant function • Function_5 = (-. 5*((current_entry-mean_5)*inv(cov_5)*(current_entry-mean_5)'))(. 5*(log(det(cov_5))))+(log(. 2)); %Table_0 discriminant function • • • [C, I] = max([Function_1, Function_2, Function_3, Function_4, Function_5]); Decision(i, 1)= I; end

Results • Accuracy • Prior Probability

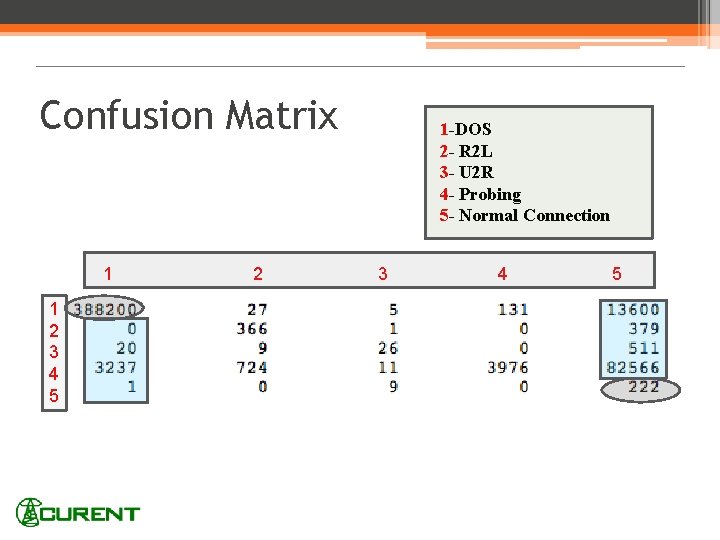
Confusion Matrix 1 1 2 3 4 5 2 1 -DOS 2 - R 2 L 3 - U 2 R 4 - Probing 5 - Normal Connection 3 4 5

1 1 2 3 4 5

• Error • Future Improvements

References • [1]Mukherjee, B. ; Heberlein, L. T. ; Levitt, K. N. ; , "Network intrusion detection, " Network, IEEE , vol. 8, no. 3, pp. 26 -41, May-June 1994 doi: 10. 1109/65. 283931 URL: http: //ieeexplore. ieee. org. proxy. lib. utk. edu: 90/stamp. jsp? tp=&arnumber=28 3931&isnumber=7023 • [2]Jain, A. K. ; Duin, R. P. W. ; Jianchang Mao; , "Statistical pattern recognition: a review, " Pattern Analysis and Machine Intelligence, IEEE Transactions on , vol. 22, no. 1, pp. 4 -37, Jan 2000 doi: 10. 1109/34. 824819 URL: http: //ieeexplore. ieee. org. proxy. lib. utk. edu: 90/stamp. jsp? tp=&arnumber=82 4819&isnumber=17859 • [3]Anonymous. Maximum Security: A Hacker's Guide to Protecting Your Internet Site and Network, Chapter 15, pp. 359 -362. Sams. net , 201 West 103 rd Street, Indianapolis, IN, 46290. 1997. • [4] Simson Garfinkel and Gene Spafford. Practical Unix & Internet Security. O'Reilly & Associates, Inc. , 101 Morris Street, Sebastopol CA, 95472, 2 nd edition, April 1996. • [5]. N. p. , n. d. Web. 10 Jul 2012. <http: //www. ll. mit. edu/mission/communications/ist/corpora/ideval/docs/attack. DB. html • [6]Joyce, James, "Bayes' Theorem", The Stanford Encyclopedia of Philosophy (Fall 2008 Edition), Edward N. Zalta (ed. ), URL = <http: //plato. stanford. edu/archives/fall 2008/entries/bayes-theorem/>.