CV Matching in 2 D Matching 2 D

CV: Matching in 2 D Matching 2 D images to 2 D images; Matching 2 D images to 2 D maps or 2 D models; Matching 2 D maps to 2 D maps MSU CSE 803 Stockman

2 D Matching n Problem 1) Need to match images to maps or models 2) need to match images to images n Applications 1) land use inventory matches images to maps 2) object recognition matches images to models 3) comparing X-rays before and after surgery MSU CSE 803 Stockman

Methods for study n n n n Recognition by alignment Pose clustering Geometric hashing Local focus feature Relational matching Interpretation tree Discrete relaxation MSU CSE 803 Stockman

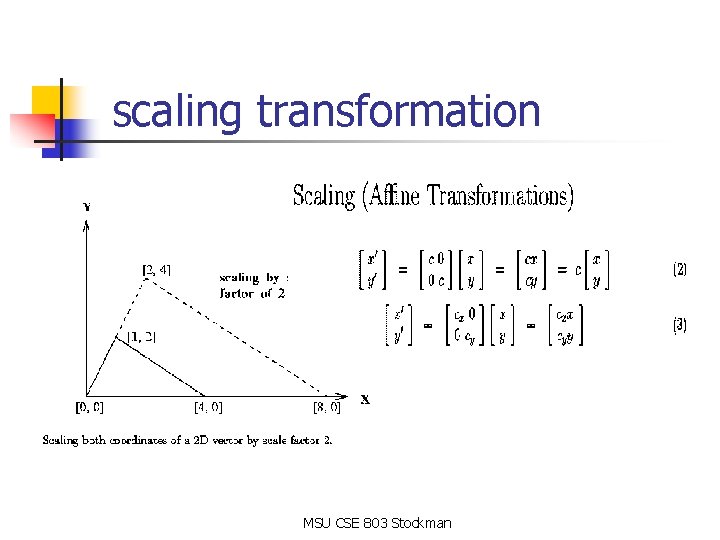
Tools and methods n n Algebra of affine transformations scaling, rotation, translation, shear Least-squares fitting Nonlinear warping General algorithms graph-matching, pose clustering, discrete relaxation, interpretation tree MSU CSE 803 Stockman

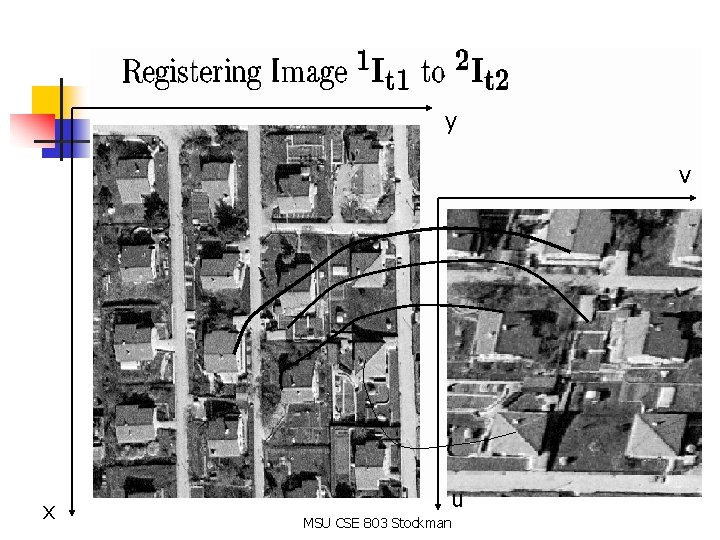
Alignment or registration DEF: Image registration is the process by which points of two images from similar viewpoints of essentially the same scene are geometrically transformed so that corresponding features of the two images have the same coordinates MSU CSE 803 Stockman

y v x u MSU CSE 803 Stockman

11 matching control points x, y, u, v below =T [ u, v, 1] = T [x, y, 1] MSU CSE 803 Stockman t

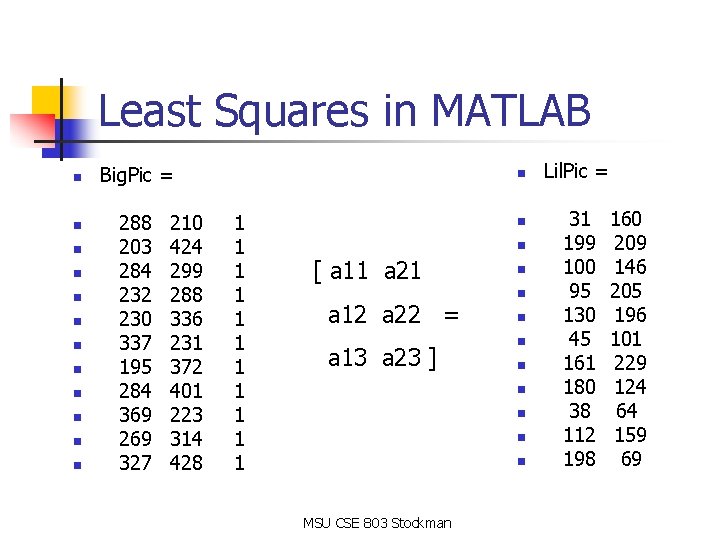
Least Squares in MATLAB n n n Big. Pic = 288 203 284 232 230 337 195 284 369 269 327 210 424 299 288 336 231 372 401 223 314 428 n 1 1 1 n n [ a 11 a 21 a 12 a 22 = a 13 a 23 ] n n n n n MSU CSE 803 Stockman Lil. Pic = 31 199 100 95 130 45 161 180 38 112 198 160 209 146 205 196 101 229 124 64 159 69

Least squares in MATLAB 2 n >> AFFINE = Big. Pic Lil. Pic n >> ERROR = Lil. Pic - Big. Pic * AFFINE n ERROR = n n n AFFINE = -0. 0414 -1. 1203 0. 7728 -0. 2126 -119. 1931 526. 6200 n n n n -0. 1855 -1. 0863 -0. 1323 1. 2175 -0. 9608 -0. 3877 0. 7696 1. 0396 0. 1188 -0. 3452 -0. 0477 n The solution is such that n the 11 D vector at the right has the smallest L 2 norm MSU CSE 803 Stockman 0. 6821 -0. 0446 1. 1239 -0. 4715 -1. 5064 1. 0428 -0. 0633 0. 8111 -1. 8080 0. 5084 -0. 2745 Worst is 1. 8 pixels

Least squares in MATLAB 3 n n n X= 288 203 284 232 210 424 299 288 >> Y Y= 31 199 100 95 160 209 146 205 1 1 Solution from 4 points has smaller error on those points n >> T = X Y n T= n n n -0. 0620 -1. 0917 0. 7592 -0. 2045 -109. 8863 517. 2541 n >> E = Y - X*T n E= n n MSU CSE 803 Stockman -0. 6846 0. 0974 -0. 4327 0. 0616 0. 4959 -0. 0706 0. 6214 -0. 0884

Least squares in MATLAB 4 When the affine transformation obtained from 4 matching points is applied to all 11 points, the error is much worse than when the transformation was obtained from those 11 points. n >> E 2 = Lil. Pic - Big. Pic * T n E 2 = n n n MSU CSE 803 Stockman -0. 6846 -0. 4327 0. 4959 0. 6214 -0. 9456 0. 4115 0. 5508 3. 0546 1. 4706 0. 1769 3. 2231 0. 0974 0. 0616 -0. 0706 -0. 0884 -1. 4568 -1. 1150 0. 6949 -1. 2135 -4. 8164 -0. 3789 -3. 7493

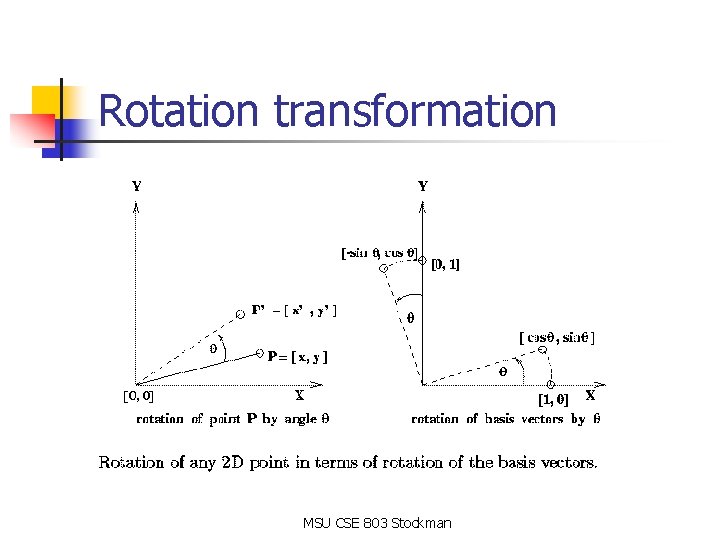
Components of transformations Scaling, rotation, translation, shear MSU CSE 803 Stockman

scaling transformation MSU CSE 803 Stockman

Rotation transformation MSU CSE 803 Stockman

Pure rotation MSU CSE 803 Stockman

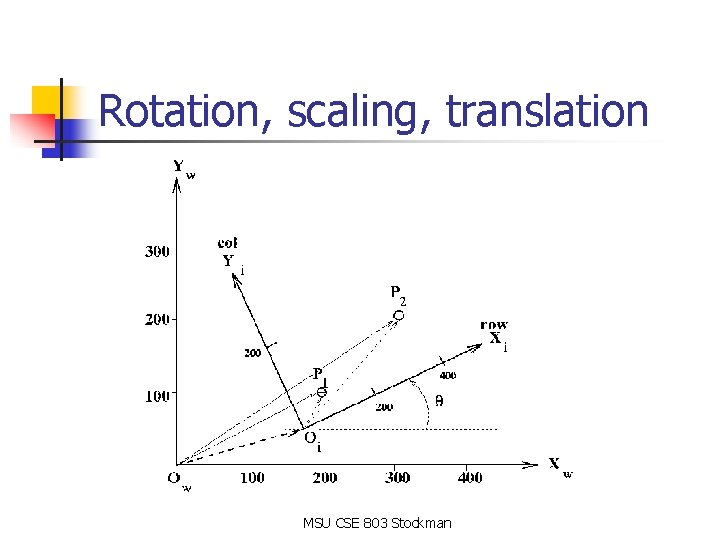
Orthogonal tranformations n n n DEF: set of vectors is orthogonal if all pairs are perpendicular DEF: set of vectors is orthonormal if it is orthogonal and all vectors have unit length Orthogonal transformations preserve angles Orthonormal transformations preserve angles and distances Rotations and translations are orthonormal DEF: a rigid transformation is combined rotation and translation MSU CSE 803 Stockman

Translation requires homogeneous coordinates MSU CSE 803 Stockman

Rotation, scaling, translation MSU CSE 803 Stockman

Model of shear MSU CSE 803 Stockman

General affine transformation MSU CSE 803 Stockman

Solving for an RST using control points MSU CSE 803 Stockman

Extracting a subimage by subsampling MSU CSE 803 Stockman

Subsampling transformation MSU CSE 803 Stockman

subsampling At MSU, even the pigs are smart. MSU CSE 803 Stockman

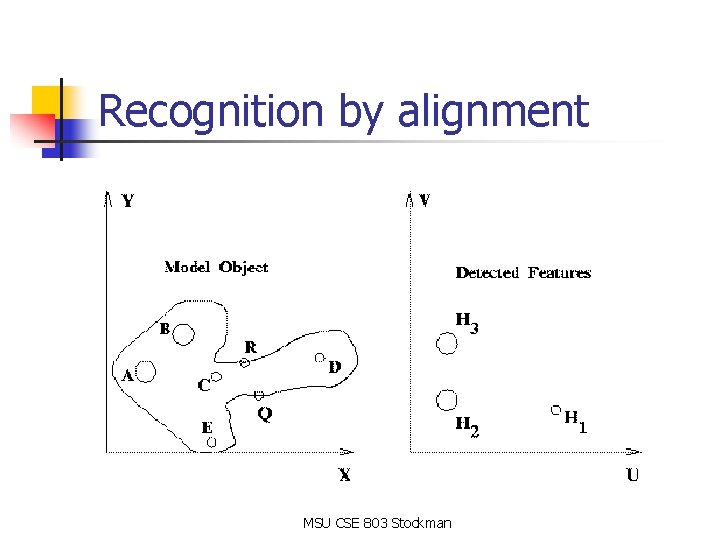
recognition by alignment n n Automatically match some salient points Derive a transformation based on the matching points Verify or refute the match using other feature points If verified, then registration is done, else try another set of matching points MSU CSE 803 Stockman

Recognition by alignment MSU CSE 803 Stockman

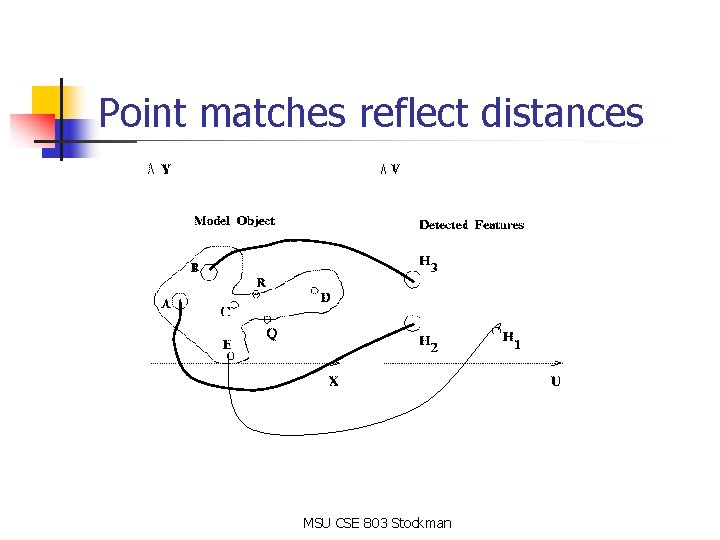
Feature points and distances MSU CSE 803 Stockman

Image features pts and distances MSU CSE 803 Stockman

Point matches reflect distances MSU CSE 803 Stockman

Once matching bases fixed n n n can find any other feature point in terms of the matching transformation can go back into image to explore for the holes that were missed (C and D) can determine grip points for a pick and place robot ( transform R and Q into the image coordinates) MSU CSE 803 Stockman

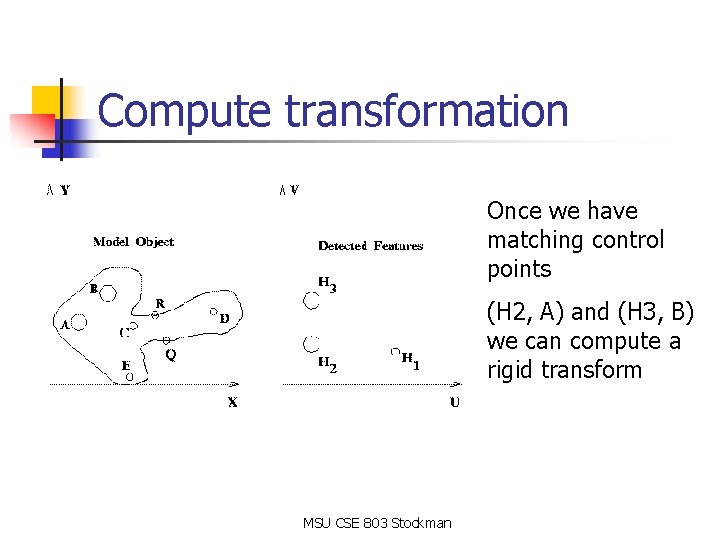
Compute transformation Once we have matching control points (H 2, A) and (H 3, B) we can compute a rigid transform MSU CSE 803 Stockman

Get rotation easily, then translation MSU CSE 803 Stockman

Generalized Hough transform Cluster evidence in transform parameter space MSU CSE 803 Stockman

See plastic slides matching maps to images MSU CSE 803 Stockman

“Best” affine transformation from overdetermined matches MSU CSE 803 Stockman

“Best” affine transformaiton Use as many matching pairs ((x, y)(u, v)) as possible MSU CSE 803 Stockman

result for previous town match MSU CSE 803 Stockman