Cutting Stock Problem Problem of cutting an unlimited

Cutting Stock Problem • Problem of cutting an unlimited number of pieces of material (paper rolls, for instance) of length l to produce ni pieces of length li , i = 1, 2, …, I. • The objective is to minimize the number of pieces of material to meet the demands. • Note: minimize number of pieces ≡ minimize total waste

• Cutting pattern Pj (j = 1, 2, …, NJ) corresponds to a specific way of cutting a piece of material: aij = number of pieces of length li produced with cutting pattern Pj where aij ≥ 0 and integer, i = 1, 2, …, I

• Mathematical Model where xj represents the number of pieces of material cut with the pattern j

• Integer programming problem difficult to solve. • Drop the constraints that the xj are required to be integer • When the demands ni are large, little is lost with respect to optimality by rounding the solution obtained by solving the relaxed problem

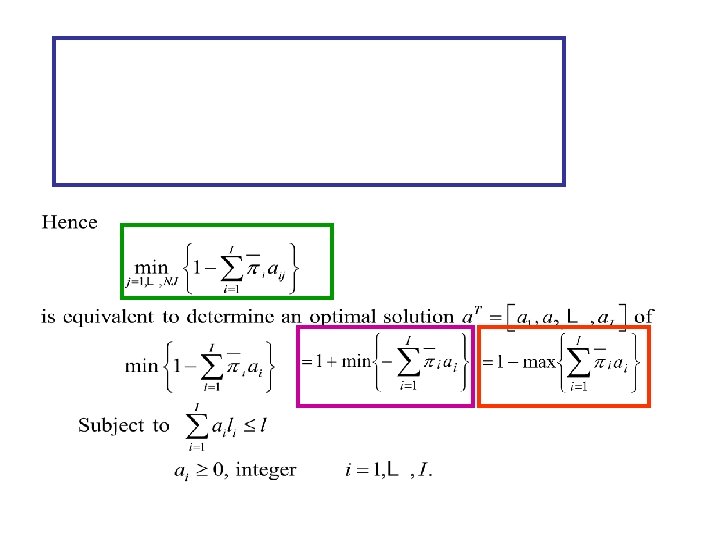
• The number NJ of patterns may be very large. For problems where the piece of material have length l = 800 cm. , and where there are demands for 40 different lengths li from 20 cm. to 80 cm. , the number of admissible patterns can easily reach 10 to 100 millions. • Interest to solve this problem using column generation. • At each iteration, a subset of patterns specify a restricted problem of are available to

Solve the restricted problem.