Customizing DSP algorithms does not always mean speed

Customizing DSP algorithms does not always mean speed A look at DFT / FFT issues M. R. Smith, Electrical and Computer Engineering, University of Calgary, Alberta, Canada smithmr@ucalgary. ca 5/22/2021 1

Overview n Introduction n Industrial Example of DFT/FFT n n n DFT -- FFT Theory Straight application Proper application “The KNOW-WHEN” application Future Talks n n The implications on DSP processor architecture How are actual DSP processors optimized for FFT operations? 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 2

References n n n Work originally done for “Beta Monitors”, Calgary Talk first given to AMD FAE Meeting, Santa Clara Published in Microprocessors and Microsystems FFT - f. RISCy Fourier Transforms n Copy made available 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 3

Testing and using DSP Algorithms n Typical testing pattern -- use something simple n n Simple test of algorithm correctness Time Signal = sum of sinusoids In test, expect, and get, sharp peaks in spectrum Algorithms used in my research n n DFT -- Discrete Fourier Transform FFT -- Fast Fourier Transform ARMA -- Autoregressive Moving Average Wavelet 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 4

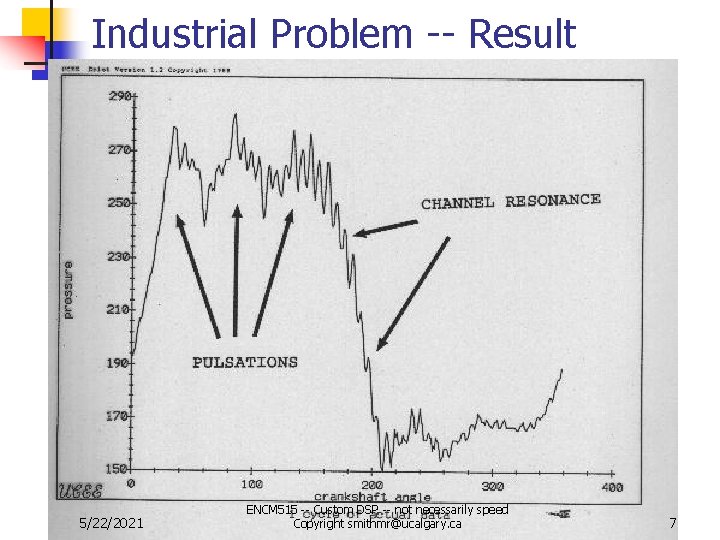
Testing and using DSP Algorithms n Typical testing pattern n n Simple test of algorithm correctness Time Signal = sum of sinusoids In test, expect, and get, sharp peaks in spectrum IN REAL LIFE -- this is not a valid test as following example shows and many people working in the field don’t get the best out of their algorithms because they don’t realize that. DFT -- Discrete Fourier Transform n n Implemented directly (Order(N x N) ) operations Implemented by FFT (Order(N x log 2 N)) 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 5

Industrial Example -- Equipment 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 6

Industrial Problem -- Result 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 7

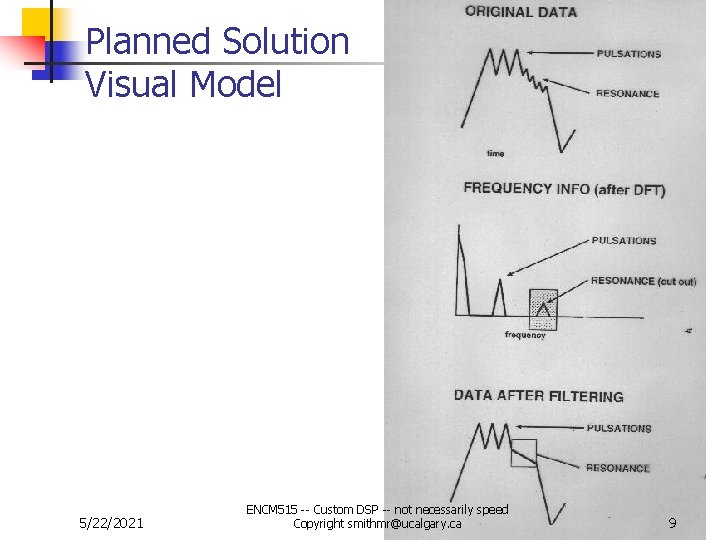
Planned Solution -- Theory n n Unwanted “noise” on a data set can be removed if the “noise” has particular frequency characteristics Improvement is obtained n n n By transforming to the frequency domain, Cutting out (filtering) the unwanted “noise” and then, Inverse transforming to recover the original data form Actually faster to operate in Frequency domain than Time domain (You can show algorithms to be equivalent) Frequency domain -- more memory needed 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 8

Planned Solution Visual Model 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 9

What algorithm could be used n Time domain filtering n n n 40 -- 300 tap FIR N = size of the data (1000+ -- infinite) Complexity Order(N x Tap Length) n n 1024 * 300 = 300, 000 operations Frequency domain filtering n n N-sized DFT Complexity n n Direct FFT 5/22/2021 Order(2 * N) = 2, 000 operations Order(2 * (N log N)) = 20, 000 operations ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 10

Direct DFT and FFT Time savings -- Number of complex multiplications N 4 32 128 1024 DIRECT 16 1024 16384 1048576 Radix 2 4 80 448 5120 %Change 400% 1300% 2100% 20488% Key issue -- How can you handle the memory accesses and operations associated with the complex multiplications of data and Fourier Coefficients? -Data/Instruction Conflicts 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 11

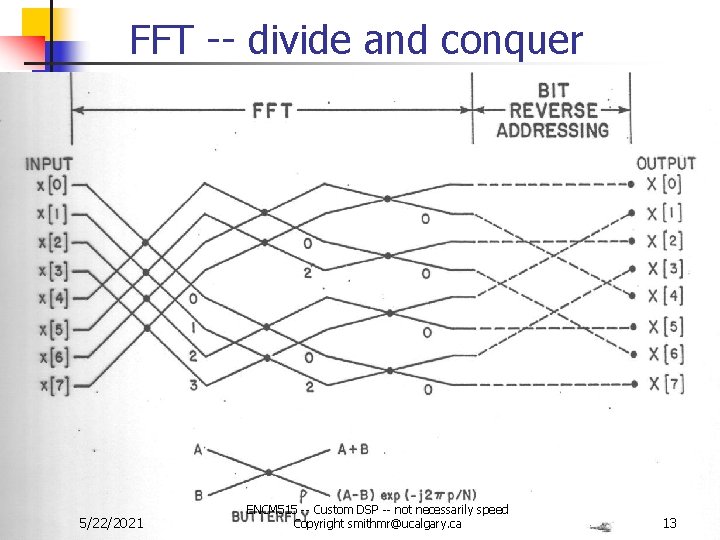
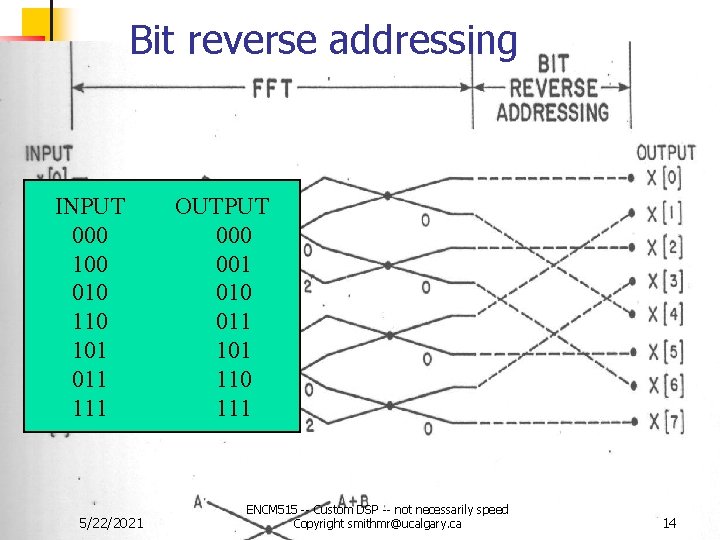
Fast DFT algorithm implementation n n DFT -- Require Order(N ^ 2) FFT -- Divide and Conquer Principle n n N pt DFT can be decimated into 2 of N/2 pt DFT plus “some twiddling on N terms” N/2 pt DFT = 2 * N/4 DFT “plus twiddling” N/4 pt DFT = 2 * N / 8 etc Order(N x log N) PROVIDED you can handle bit reverse addressing efficiently 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 12

FFT -- divide and conquer 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 13

Bit reverse addressing INPUT 000 100 010 101 011 111 5/22/2021 OUTPUT 000 001 010 011 101 110 111 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 14

Algorithm -- Different forms x, y == real/imaginary parts of the input wr, wi = precalculated cosine/sine values m = log 2(N) where N is the number of points (power of 2) n 2 = N for (k = 0; k < m; k++) { n 1 = n 2; n 2 = n 2 / 2; /* Outer loop */ ie = n / n 1; ia = 1; for (j = 0; j < n 2; j++) { c = wr[ia]; s = wi[ia]; for (i = j; i < N; i += n 1) { l = i + n 2 xt = x[i] - x[l]; yt = y[i] - y[l]; x[i] += x[l]; y[i] += y[l]; x[l] = c * xt + s * yt; y[l] = c * yt - s * xt; } } } 5/22/2021 /* Middle loop */ ia += ie; /* inner loop */ /* Butterfly offset */ /* Common */ /* Upper */ /* Lower */ ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 15

What processors can be used? n CISC n n n DSP n n n Digital signal processing chip Specifically designed for DSP Specialized resources provided Dual cycle instructions (many now one) RISC n n 5/22/2021 Complex instruction set processor Basic and complex functions Control logic requires much real estate Many cycle instructions Reduced instruction set processor Simple instructions done well Instructions complete in single cycle Intelligent compiler needed ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 16

Real life application of Theory n n n n Take 370 data points Pad to 512 with zeros to size of algorithm Use standard FFT algorithm Zero unwanted “noise” components Use standard inverse FFT Transform “Angle” measurement to “Volume” Area between hystersis loop is associated with compressor efficiency 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 17

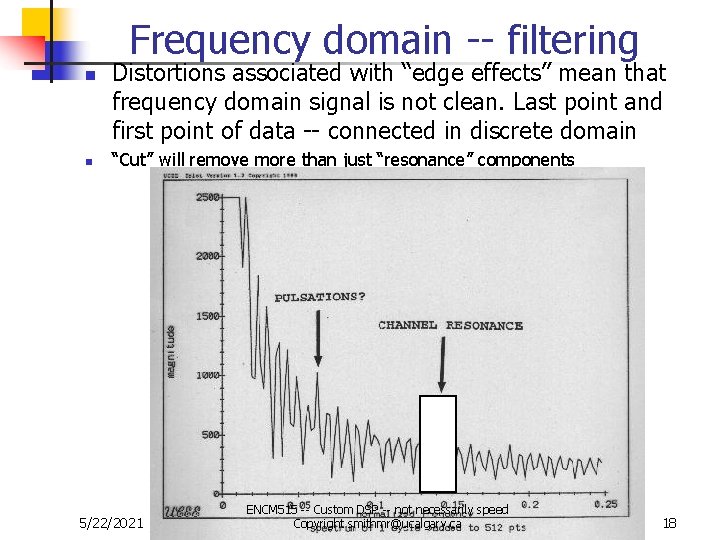
Frequency domain -- filtering n n Distortions associated with “edge effects” mean that frequency domain signal is not clean. Last point and first point of data -- connected in discrete domain “Cut” will remove more than just “resonance” components 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 18

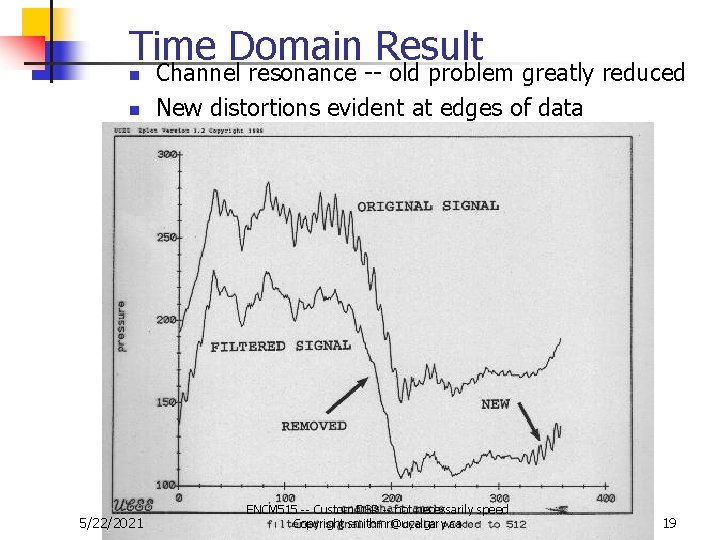
Time Domain Result n n 5/22/2021 Channel resonance -- old problem greatly reduced New distortions evident at edges of data ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 19

Real Life versus Theory n Perfect data n n n infinitely long perfectly sampled Actual data n n Nyquist must be met (sample fast enough to cover signal and noise characteristics) finite length of the data manipulated n 5/22/2021 Can be analysed using Fourier Theory by treating as infinitely long signal multiplied by a square window ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 20

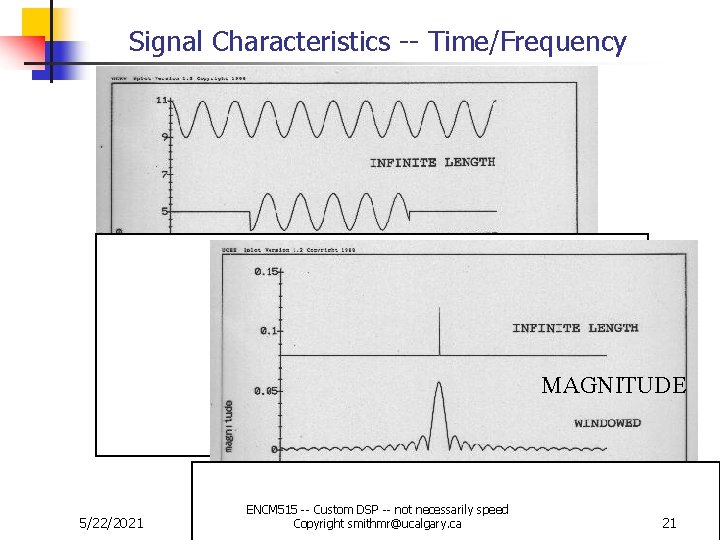
Signal Characteristics -- Time/Frequency MAGNITUDE 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 21

Windowing -- implied and deliberate n Windowing the data in the “TIME” domain spreads the “SPECTRUM” n n MAIN LOBE -- width of main lobe determines resolutions, or how close two similar sized peaks can be placed but yet be separated SIDE LOBES -- height of side lobes determine how close a small peak can be placed to a large peak and be believed as not being a “false” peak (side lobe) Choose a window with the narrowest main lobe and smallest side lobe MRI, seismic, telecommunications all have similar problems This form of data distortion often missed by naive users KEY REFERENCE -- HARRIS -- Proc. IEEE 666, p 51, 1978 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 22

Windowing occurs -- when? n ALL DATA ANYBODY GATHERS is always windowed n n DFT (and many other algorithms) treat data AS CYCLIC n n n NO EXCEPTIONS -- finite length in either time or frequency domain No problems if CYCLIC model results in continuous data across the cycles (Nth order continuity is needed) Discontinuities in data cause BIG problems in frequency domain -- in particular padding with zeros in order to use any DFT algorithm Some diseases in MRI are mimicked by truncation artifacts 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 23

How to fix n n Chose a better window Naturally window n n Synchronously sample n n Take data in a way that the data goes more smoothly to zero at end Very special case -- and possible for this data set Different DSP algorithm n Not always stable -- MA, ARMA, Burg, wavelet etc. 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 24

Windows W(m) = a 0 + a 1 cos (2 PI m / N) + a 2 cos (4 PI m / N ) (0 <= m < N) BEWARE -N/2 <= m < N/2 -- flips sign of a 1 Normal (Rect. ) a 0 = 1, a 1 =0, a 2 = 0 Simple a 0 = 0. 54, a 1 = -0. 46, a 2 = 0; Blackman-Harris 3 term -- optimized a 0 = 0. 44959, a 1 = -0. 49364, a 2 = 0. 05677 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 25

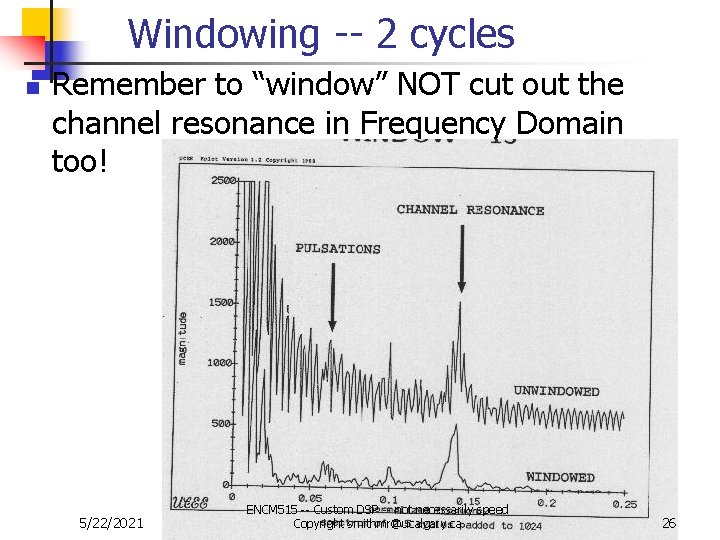
Windowing -- 2 cycles n Remember to “window” NOT cut out the channel resonance in Frequency Domain too! 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 26

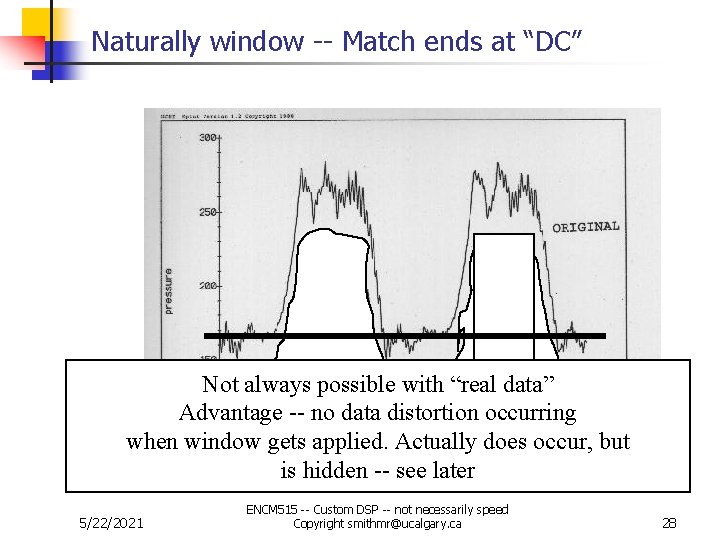
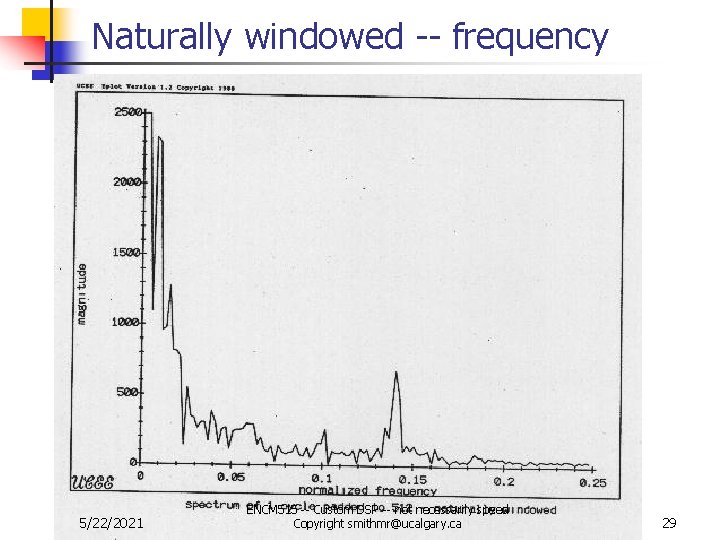
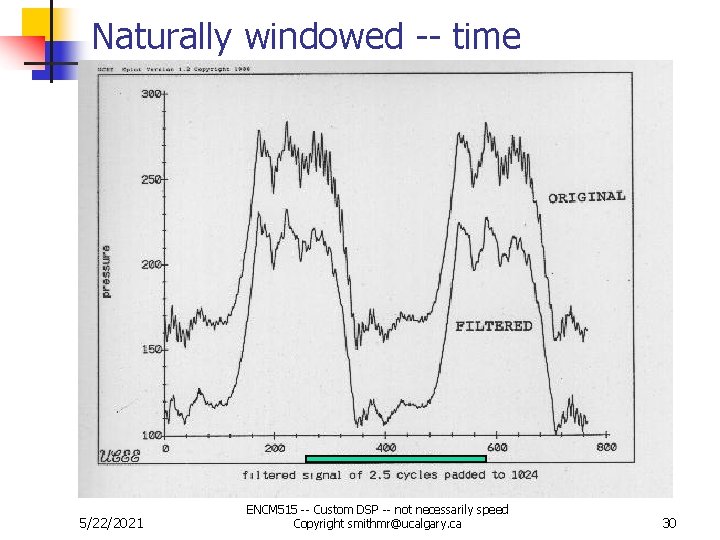
Natural Window 1. 2. n n Rearrange the way you sample so that data “naturally goes to same DC level” near ends Remove DC offset then pad with zeros Resolution between peaks in the frequency domain is function of data length. This example uses 2. 5 cycles of the original data sequence 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 27

Naturally window -- Match ends at “DC” Not always possible with “real data” Advantage -- no data distortion occurring when window gets applied. Actually does occur, but is hidden -- see later 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 28

Naturally windowed -- frequency 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 29

Naturally windowed -- time 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 30

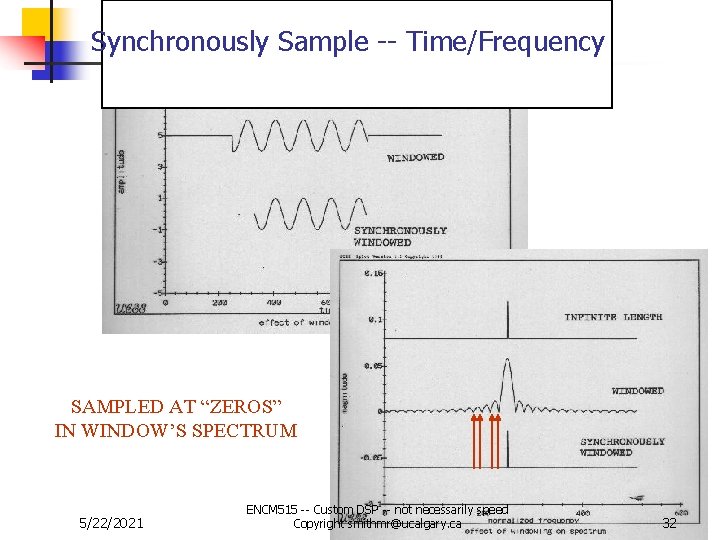
Synchronously Sample the Data n n n As an engineer, you have to be able to reach back into your “theory” and recognize when this sort of thing is possible and correct! Not a solution for most data sets There must be a “TRUE”, exact, cyclic property present in the original data set. Algorithm must be applied “exactly correctly” Windowing is still there! All the windowing distortions are still present -BUT!!!!!! ENCM 515 -- Custom DSP -- not necessarily speed 5/22/2021 Copyright smithmr@ucalgary. ca 31

Synchronously Sample -- Time/Frequency SAMPLED AT “ZEROS” IN WINDOW’S SPECTRUM 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 32

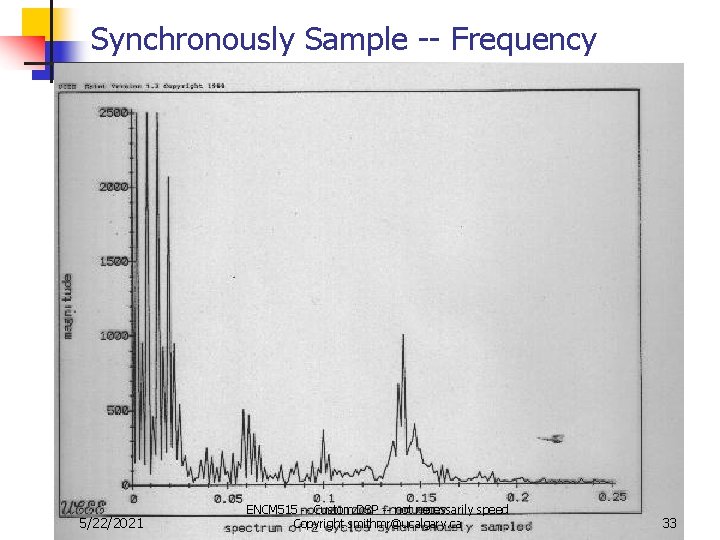
Synchronously Sample -- Frequency 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 33

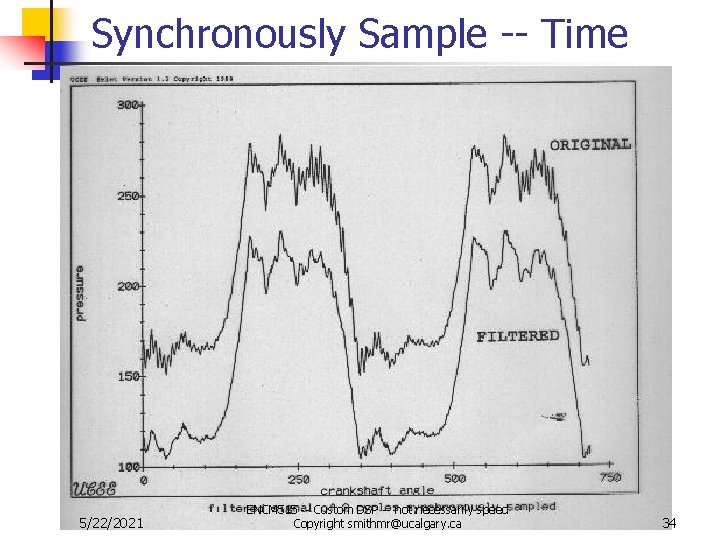
Synchronously Sample -- Time 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 34

Synchronously Sample n n Not possible for most situations There is a “TRUE” cyclic property present in data Don’t Pad with zeros -- use 740 pt DFT This industrial example n n 370 points round the cycle Would a specialized FFT algorithm improve things? (2 x 5 x 7) Implemented directly using a 740 point DFT Customer satisfied with integer implementation on Z 80 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 35

This sort of customization -- NOT NORMALLY POSSIBLE n n What are the characteristics of general DSP algorithms? What needs to be present on a processor to meet those requirements? Covered in earlier lecture See IEEE Micro Magazine, Dec. 1992 “How RISCy is DSP” 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 36

Overview n Introduction n Industrial Example of DFT/FFT n n n DFT -- FFT Theory Straight application Proper application “The KNOW-WHEN” application Future talks n n The implications on DSP processor architecture How are actual DSP processors optimized for FFT operations? 5/22/2021 ENCM 515 -- Custom DSP -- not necessarily speed Copyright smithmr@ucalgary. ca 37