Curves Bzier Spline Curve Interpolation The curve is

Curves Bézier Spline Curve

Interpolation • The curve is passing through the control points

Polynomical interpolation • Linear – 2 points • Quadratic – 3 points • Polynom n degree – n+1 points
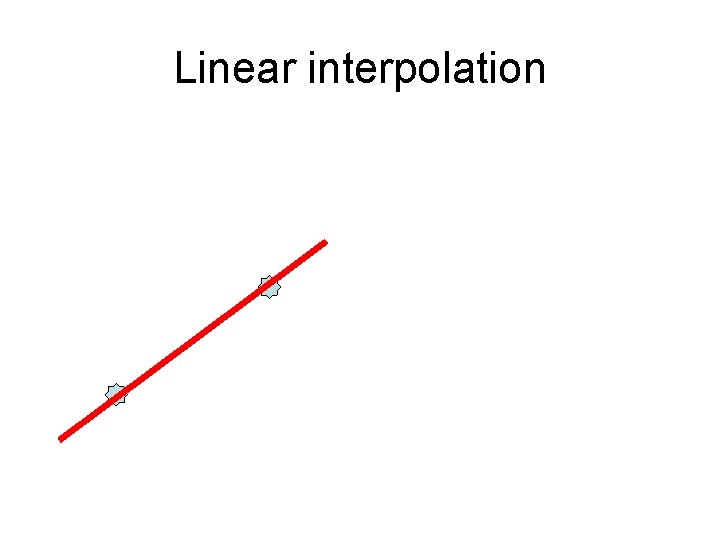
Linear interpolation
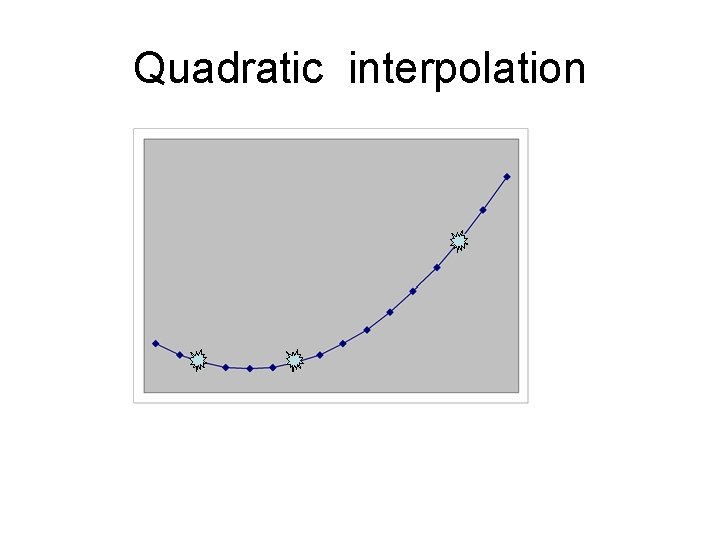
Quadratic interpolation
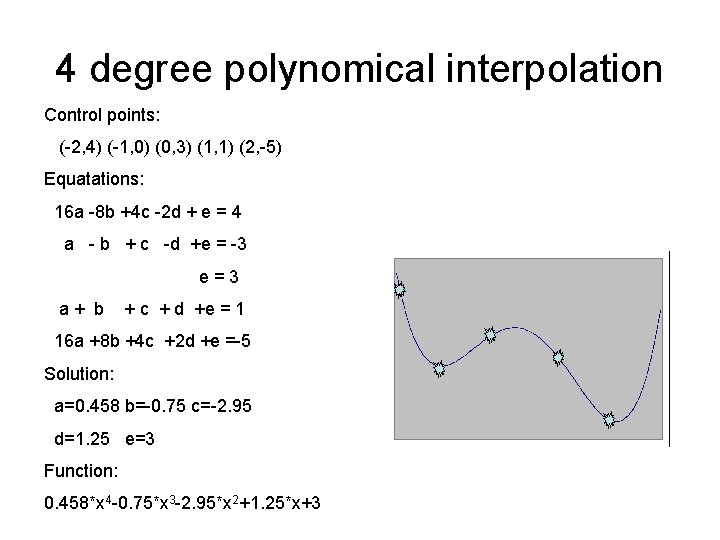
4 degree polynomical interpolation Control points: (-2, 4) (-1, 0) (0, 3) (1, 1) (2, -5) Equatations: 16 a -8 b +4 c -2 d + e = 4 a - b + c -d +e = -3 e=3 a+ b + c + d +e = 1 16 a +8 b +4 c +2 d +e =-5 Solution: a=0. 458 b=-0. 75 c=-2. 95 d=1. 25 e=3 Function: 0. 458*x 4 -0. 75*x 3 -2. 95*x 2+1. 25*x+3

Spline curve • The curve consists of segments expressed by polynom of lesser degree then the number of the points require. The curves in their border points have smooth continue.

Linear „spline“ • Polynoms of first degree. • In the border points the continuation is continuous. • But the first derivation must not be continuous. • So the curve must not be smooth. • The simple term is polyline.

Quadratic spline • The curve is formed by segments of parabolas. • In the border points there is a smooth continuation, the first derivation is continuous. • The following derivation must not be }and commonly are not) continuous. • This is the most common version of spline curve. When only spline is said the quadratic spline is understood (Auto. CAD).

Quadratic spline

Spline curves of higher degree • Cubic – curve formed by segments of 3 th degree functions (cubics), the continuation of first and second derivation is guarantee. • General (n-th degree), the continuation of (n-1)th derivation is guarantee.

Approximation curves • The curve does not necessary pass through the control points. • Formally any curve is the aproximation curve. • The main task is to find such an expression to be – Simple – To approximate the control points sufficiently well

Least squares approximation • I choose the type of the function (commonly the polynomical function of lesser degree then the necessary degree for interpolation) • I compute such parameters, so the summa of the squares of the deviations is minimal. • ∑(yi-f(xi))2→ min
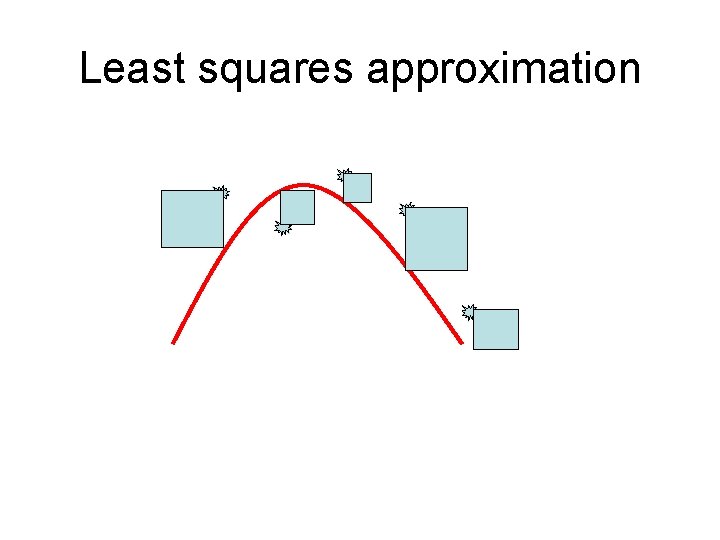
Least squares approximation

Bézier approximation (Bézier’s curve) • Approximation by a polynom of n-th degree for n+1 control points P 0, P 1, …, Pn • The curve pass through the first point P 0 and the last point Pn • The tangent in the first point P 0 is parallel to the vector P 0 P 1. • The tangent in the last point Pn is paralle to the vector Pn-1 Pn • The whole curve lies in the convex hull of the points P 0, … , Pn

Pierre Ettiene Bézier (1910 -1999)

The expression of the Bézier curve
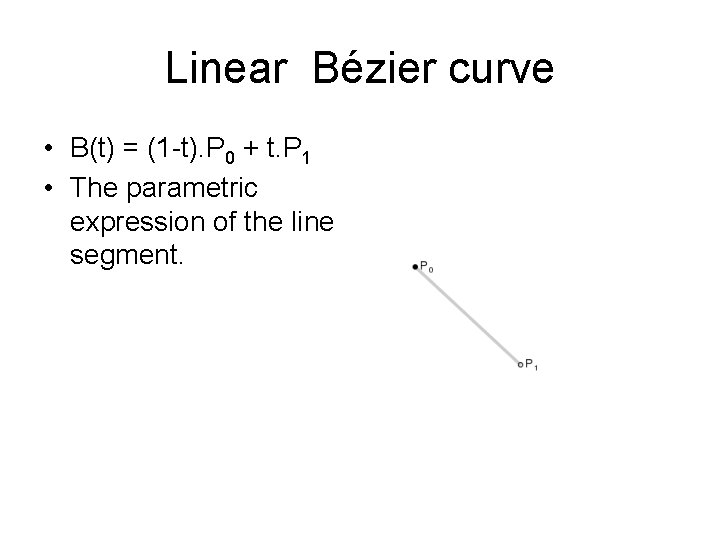
Linear Bézier curve • B(t) = (1 -t). P 0 + t. P 1 • The parametric expression of the line segment.
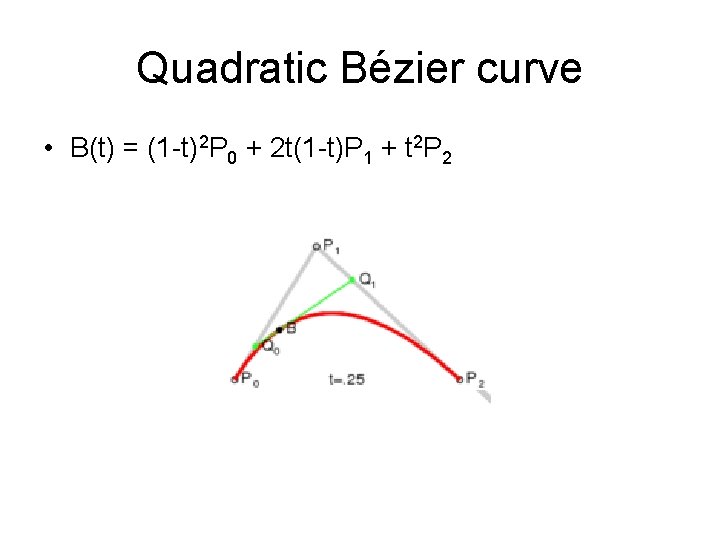
Quadratic Bézier curve • B(t) = (1 -t)2 P 0 + 2 t(1 -t)P 1 + t 2 P 2
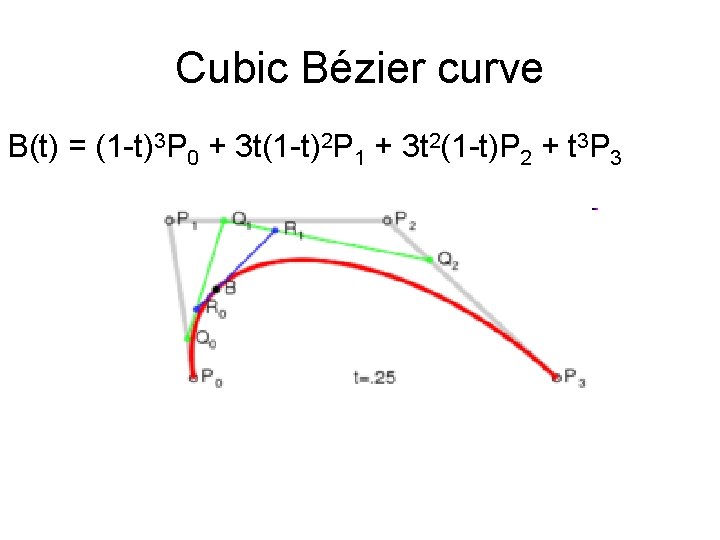
Cubic Bézier curve B(t) = (1 -t)3 P 0 + 3 t(1 -t)2 P 1 + 3 t 2(1 -t)P 2 + t 3 P 3
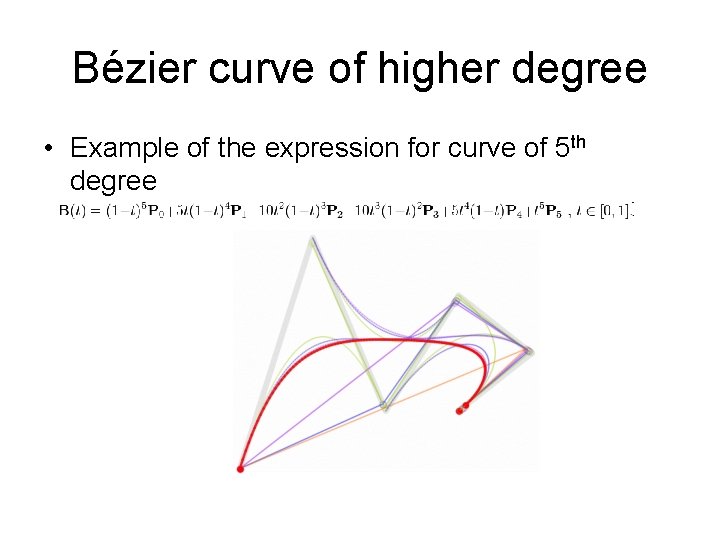
Bézier curve of higher degree • Example of the expression for curve of 5 th degree

Homework • Take a set of 4 control points (-2, -2), ( -1, 2), (1, -2), (2, 2). • Try to construct an polynomic interpolation curve passing through a set of control points • Try to construct an quadratic spline curve passing through a set of control points • Try to construct an 3 -degree Bezier curve designated by a set of control points
- Slides: 22