Curves and Surfaces in Open GL 1 Objectives

Curves and Surfaces in Open. GL 1

Objectives • Introduce Open. GL evaluators • Learn to render polynomial curves and surfaces • Discuss quadrics in Open. GL GLUT Quadrics GLU Quadrics 2

What Does Open. GL Support? • Evaluators: general mechanism for working with Bernstein polynomials Can use any degree polynomials Can use in 1 4 dimensions Automatic generation of normals and texture coordinates NURBS supported in GLU • Quadrics GLU and GLUT contain polynomial approximations of quadrics 3

One-Dimensional Evaluators • Evaluate Bernstein polynomial of any degree at set of specified values • Can evaluate variety of variables Points along 2 , 3 or 4 D curve Colors Normals Texture Coordinates • Can set up multiple evaluators all evaluated for same value 4

Setting Up an Evaluator what we want to evaluate max and min of u gl. Map 1 f(type, u_min, u_max, stride, order, pointer_to_array) separation between 1+degree of polynomial data points pointer to control data Each type must be enabled by gl. Enable(type) 5

Example Consider evaluator for cubic Bezier curve over (0, 1) point data[ ]={…………. . }; * /3 d data /* gl. Map 1 f(GL_MAP_VERTEX_3, 0. 0, 1. 0, 3, 4, data); cubic data are 3 D vertices data arranged as x, y, z, x, y, z…… three floats between data points in array gl. Enable(GL_MAP_VERTEX_3); 6

Evaluating • gl. Eval. Coord 1 f(u) causes all enabled evaluators to be evaluated for specified u Can replace gl. Vertex, gl. Normal, gl. Tex. Coord • values of u need not be equally spaced 7

Example • Consider previous evaluator set up for cubic Bezier over (0, 1) • Suppose want to approximate curve with 100 point polyline gl. Begin(GL_LINE_STRIP) for(i=0; i<100; i++) gl. Eval. Coord 1 f( (float) i/100. 0); gl. End(); 8

Equally Spaced Points Rather than use loop, can set up equally spaced mesh (grid) then evaluate it with one function call gl. Map. Grid(100, 0. 0, 1. 0); sets up 100 equally spaced points on (0, 1) gl. Eval. Mesh 1(GL_LINE, 0, 99); renders lines between adjacent evaluated points from point 0 to point 99 9

Bezier Surfaces • Similar procedure to 1 D but use 2 D evaluators in u and v • Set up with gl. Map 2 f(type, u_min, u_max, u_stride, u_order, v_min, v_max, v_stride, v_order, pointer_to_data) • Evaluate with gl. Eval. Coord 2 f(u, v) 10

Example bicubic over (0, 1) x (0, 1) point data[4][4]={………}; gl. Map 2 f(GL_MAP_VERTEX_3, 0. 0, 1. 0, 3, 4, 0. 0, 12, 4, data); Note that in v direction data points are separated by 12 floats since array data is stored by rows 11

Rendering with Lines must draw in both directions for(j=0; j<100; j++) { gl. Begin(GL_LINE_STRIP); for(i=0; i<100; i++) gl. Eval. Coord 2 f((float) i/100. 0, (float) j/100. 0); gl. End(); gl. Begin(GL_LINE_STRIP); for(i=0; i<100; i++) gl. Eval. Coord 2 f((float) j/100. 0, (float) i/100. 0); gl. End(); } 12

Rendering with Quadrilaterals can form quad mesh and render with lines for(j=0; j<99; j++) { gl. Begin(GL_QUAD_STRIP); for(i=0; i<100; i++) { gl. Eval. Coord 2 f ((float) i/100. 0, (float) j/100. 0); gl. Eval. Coord 2 f ((float)(i+1)/100. 0, (float)j/100. 0); } gl. End(): } 13

Uniform Meshes • can form 2 D mesh (grid) in similar manner to 1 D for uniform spacing gl. Map. Grid 2(u_num, u_min, u_max, v_num, v_min, v_max) • Can evaluate as before with lines or if want filled polygons gl. Eval. Mesh 2( GL_FILL, u_start, u_num, v_start, v_num) 14

Rendering with Lighting • If use filled polygons, have to shade or will see solid color uniform rendering • Can specify lights and materials but need normals Let Open. GL find them gl. Enable(GL_AUTO_NORMAL); 15

NURBS • Open. GL supports NURBS surfaces through the GLU library • Why GLU? Can use evaluators in 4 D with standard Open. GL library However, there are many complexities with NURBS that need lot of code There are five NURBS surface functions plus functions for trimming curves that can remove pieces of a NURBS surface 16

Quadrics • in both GLU and GLUT libraries Both use polygonal approximations • application specifies resolution Sphere: lines of longitude and lattitude • GLU: disks, cylinders, spheres Can apply transformations to scale, orient, and position • GLUT: Platonic solids, torus, Utah teapot, cone 17

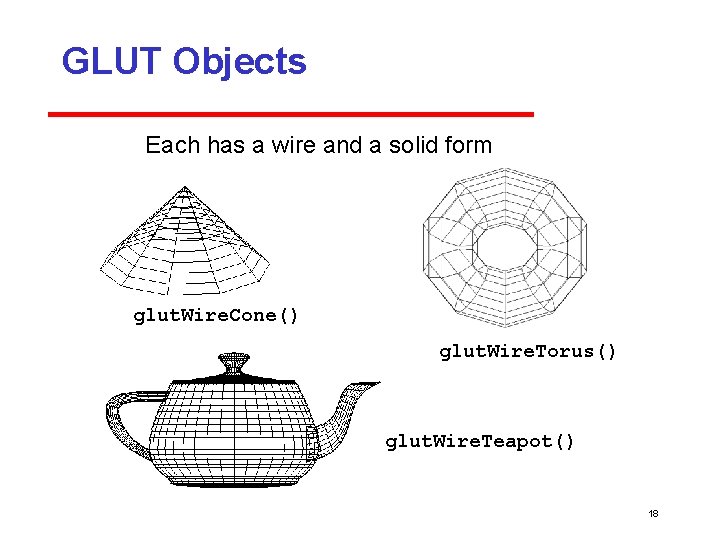
GLUT Objects Each has a wire and a solid form glut. Wire. Cone() glut. Wire. Torus() glut. Wire. Teapot() 18

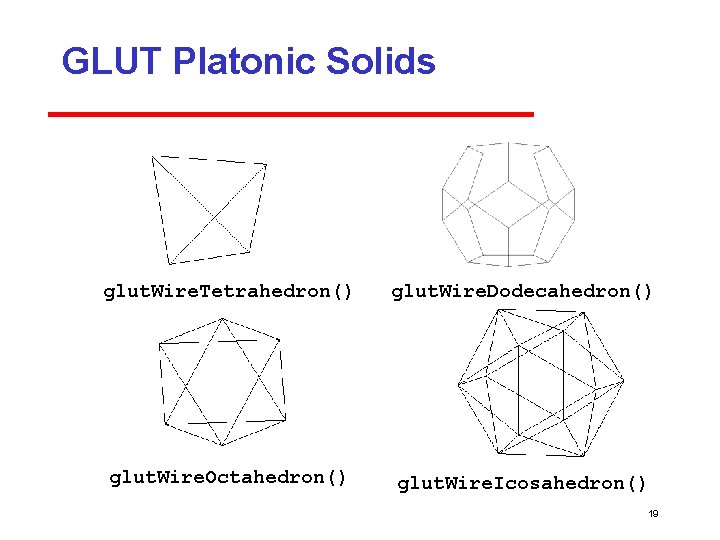
GLUT Platonic Solids glut. Wire. Tetrahedron() glut. Wire. Dodecahedron() glut. Wire. Octahedron() glut. Wire. Icosahedron() 19

Quadric Objects in GLU • GLU can automatically generate normals and texture coordinates • Quadrics are objects that include properties e. g. , how would like object to be rendered disk partial disk sphere 20

Defining a Cylinder GLUquadric. OBJ *p; P = glu. New. Quadric(); /*set up object */ glu. Quadric. Draw. Style(GLU_LINE); /*render style*/ glu. Cylinder(p, BASE_RADIUS, TOP_RADIUS, BASE_HEIGHT, sections, slices); 21