Curved Mirrors Concave Mirrors Mirrors that are a

Curved Mirrors

Concave Mirrors • Mirrors that are a small portion of the inside of a sphere • The angle of incidence still equals the angle of reflection. • Called converging mirrors • The focal length (f) is one-half the radius (R).

Concave Mirrors • The image shown is real because the reflected rays actually pass through each other. • Virtual images only appear to come from a single point. • Object distance (p) • Image distance (q) • Object height (h) • Image height (h’)

Ray Tracing for a Concave Spherical Mirror Click below to watch the Visual Concept

Concave Spherical Mirrors • Image close to a concave mirror appear: • Larger than the object • Upright

Concave Spherical Mirrors • Image far from a concave mirror appear: • Smaller than the object • Inverted or upside down

Concave Spherical Mirrors • Another factor that influence image appearance is: • Curvature • R = radius of curvature or/ radius of the spherical mirror • C = center of curvature of the mirror

Concave Spherical Mirrors • Image location can be found using the mirror equation: • (1/p) + (1/q) = (2/r)

Concave Spherical Mirrors • Two kinds of images • Real- images that form in front of the mirror • Virtual- images that form behind the mirror

Concave Spherical Mirrors • Another factor that influence image appearance is: • Curvature • R = radius of curvature or/ radius of the spherical mirror • C = center of curvature of the mirror

Concave Spherical Mirrors • The FOCAL POINT (F) is half way between the center of curvature and the mirrors surface • The distance to the focal point is the focal length (f) • (1/p) + (1/q) = (1/f)

Rules of the Mirror Equation • Real images form on the front side of the mirror • Virtual images form on the back side of the mirror • The mirror is drawn so the front side is on the left

Rules of the Mirror Equation • Positive numbers indicate the front side of the mirror • Negative numbers indicate the back side of the mirror • The principal axis runs through the center of the mirror

Rules of the Mirror Equation • Positive numbers are above the principal axis • Negative numbers are below the principal axis

Mirror Equation • h is positive if it is upright and negative when inverted. • M is positive for virtual (upright) images.

Magnification • M is positive means the image is upright • M is negative means the image is inverted

Concave Mirrors • These rules describe three rays that are easily drawn without the need to measure angles. • Others can be drawn after the image point is located using at least two of these rays.

Concave Mirrors • Is the image real or virtual? Inverted or upright? Larger than or smaller than or equal to the object in size?

Concave Mirrors • Is the image real or virtual? Inverted or upright? Larger than or smaller than or equal to the object in size?

Concave Mirrors • Is the image real or virtual? Inverted or upright? Larger than or smaller than or equal to the object in size?

Concave Mirrors • Is the image real or virtual? Inverted or upright? Larger than or smaller than or equal to the object in size?

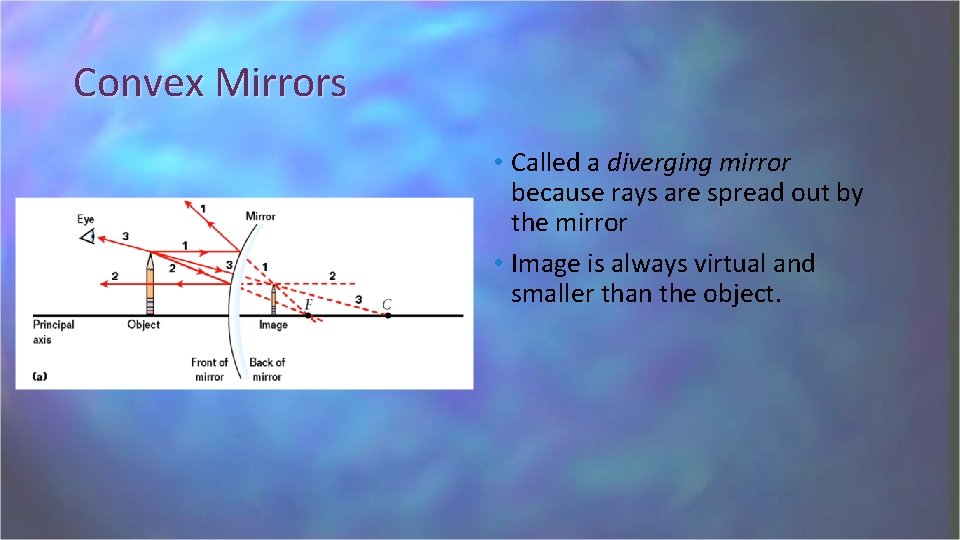
Convex Mirrors • Called a diverging mirror because rays are spread out by the mirror • Image is always virtual and smaller than the object.

Convex Mirrors • Used as side-view mirrors on cars • What warning is written on these mirrors? Why? • Images are small so they appear to be farther away. • Also used in stores to monitor shoppers • Equations are the same as those for concave mirrors.

Ray Tracing for a Convex Spherical Mirror Click below to watch the Visual Concept

Practice Problem • A concave makeup mirror is designed so that a person 25. 0 cm in front of it sees an upright image at a distance of 50. 0 cm behind the mirror. What is the radius of curvature of the mirror? What is the magnification of the mirror? Is the image real or virtual?

Practice Problem • A concave shaving mirror has a focal length of 33 cm. Calculate the position of a cologne bottle placed in front of the mirror at a distance of 93 cm. Calculate the magnification of the image. Is the image upright or inverted? Is the image real or virtual? Draw a ray diagram.

Practice Problem • A pen in placed 11. 0 cm from a concave mirror produces a real image of 13. 2 cm from the mirror. What is the focal length of the mirror? Calculate the magnification of the image. If the pen is placed 27. 0 cm from the mirror, what is the new position of the image? What is the magnification of the new image? Is the image upright or inverted? Is the image real or virtual? Draw a ray diagram.

Practice Problem • A convex mirror with a radius of curvature of 0. 550 m is placed above the aisle in a store. Determine the image distance and magnification of a customer lying on the floor 3. 1 m below the mirror. Is the image virtual or real? Is the image inverted or upright?

Practice Problem • A spherical glass ornament is 6. 00 cm in diameter. If an object is placed 10. 5 cm from the ornament, where will its image form? What is the magnification? Is the image virtual or real? Is the image inverted or upright? Draw a diagram.

Practice Problem • What is the image distance for an automobile 5. 5 m in front of a convex mirror with a 0. 25 m focal length? What is the magnification? Is the image virtual or real? Is the image inverted or upright? Draw a diagram.

Practice Problem • A soda bottle is placed 44 cm from a convex mirror. If the mirror’s focal length is 33 cm, how far from the mirror’s surfaced does the bottle’s image form? What is the magnification? Is the image virtual or real? Is the image inverted or upright? Draw a diagram.

Parabolic Mirrors • With spherical mirrors, rays not near the principal axis do not all meet at the image point. • Parabolic mirrors eliminate this problem and produce sharper images.

Parabolic Mirrors & Spherical Aberration • Using rays near the axis on spherical mirrors reduces the aberration or blurriness of the image. • A very small section of a sphere is nearly identical to a paraboloid. • Parabolic mirrors are used in telescopes to sharpen the image.

Reflecting Telescope Click below to watch the Visual Concept