CURVE SKETCHING Section 3 6 Calculus APDual Revised

  • Slides: 59
Download presentation
CURVE SKETCHING Section 3. 6 Calculus AP/Dual, Revised © 2013 viet. dang@humble. k 12.

CURVE SKETCHING Section 3. 6 Calculus AP/Dual, Revised © 2013 viet. dang@humble. k 12. tx. us 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 1

REVIEW Given f(x) = x 4 – 4 x 3, find the relative extrema

REVIEW Given f(x) = x 4 – 4 x 3, find the relative extrema 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 2

REVIEW Given f(x) = x 4 – 4 x 3, find the absolute extrema

REVIEW Given f(x) = x 4 – 4 x 3, find the absolute extrema from [– 1, 1] 1/12/2022 5: 26 AM 3. 6 – Curve Sketching x y – 1 5 0 0 1 – 3 3

10 KEYS TO GRAPHING FUNCTIONS A. B. C. D. E. F. G. H. I.

10 KEYS TO GRAPHING FUNCTIONS A. B. C. D. E. F. G. H. I. x–intercept (let y = 0) y–intercept (let x = 0) Symmetry Vertical Asymptotes (let Denominator equal to 0) and Horizontal Asymptotes (B/S = Slant Asymptote, S/B = 0, Same: “Co”) Identify all Critical Values First Derivative and Second Derivative Chart with justification Identify all relative/local and absolute maximums and minimums Identify all concavity Domain (interval notation) and Range in Interval Notation Graphs with appropriate scale with labeled f(x), f '(x), and f "(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 4

GUIDELINES OF ANALYZING A GRAPH A. B. C. D. E. F. G. Determine domain

GUIDELINES OF ANALYZING A GRAPH A. B. C. D. E. F. G. Determine domain and range Find f '(x) and f ''(x) Find the critical numbers of f, and identify the function's behavior at each one Find where the curve is increasing and decreasing Find the points of inflection, if any, and determine concavity of curve Identify any asymptotes Plot key points, such as intercepts and points 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 5

REVIEW A. First Derivative Test 1. Positive: Curve is Rising 2. Negative: Curve is

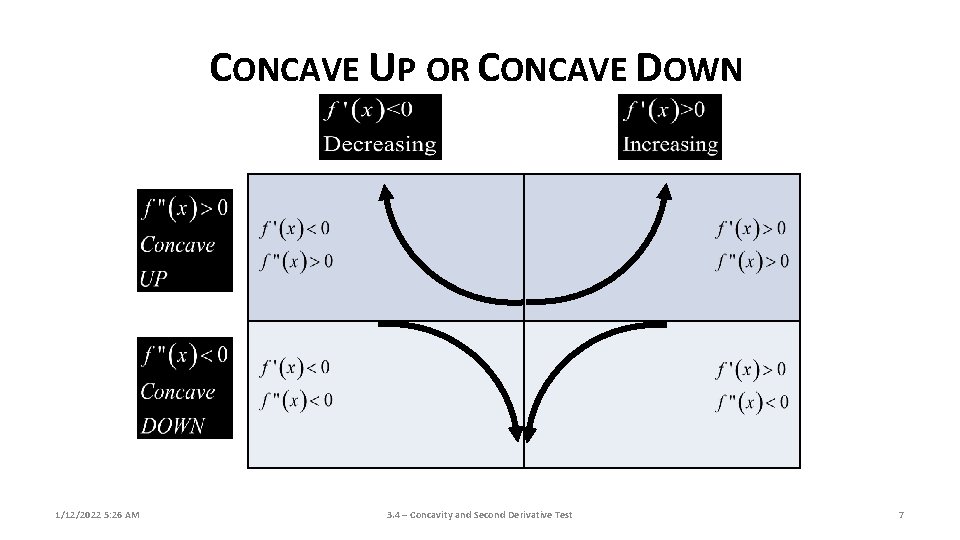
REVIEW A. First Derivative Test 1. Positive: Curve is Rising 2. Negative: Curve is Falling 3. Zero: Local/Relative Minimum or Maximum B. Second Derivative Test with Critical Values 1. Positive: Concave Up 2. Negative: Concave Down 3. Zero: Go back to the First Derivative Test 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 6

CONCAVE UP OR CONCAVE DOWN 1/12/2022 5: 26 AM 3. 4 – Concavity and

CONCAVE UP OR CONCAVE DOWN 1/12/2022 5: 26 AM 3. 4 – Concavity and Second Derivative Test 7

EXAMPLE 1 The graph of function f(x) is given. Establish the x and y–intercept(s),

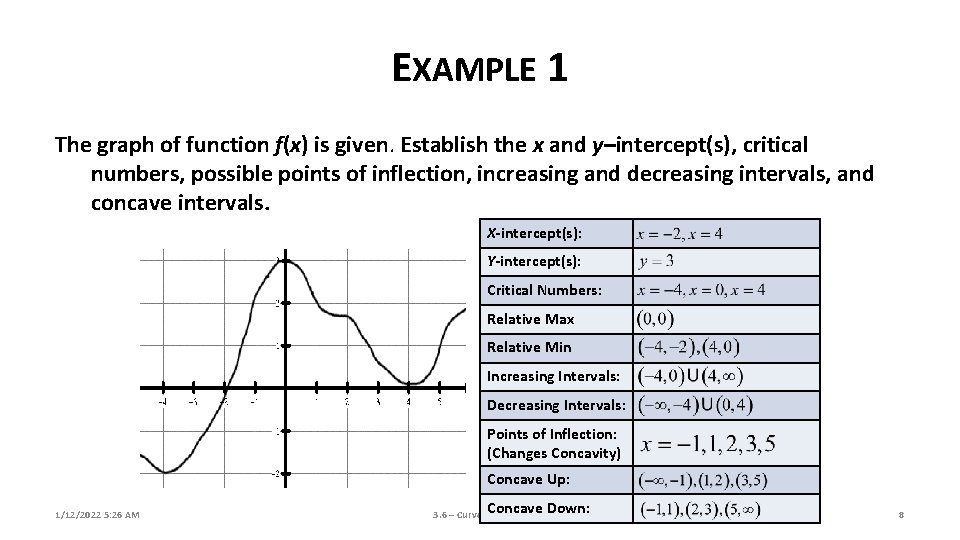
EXAMPLE 1 The graph of function f(x) is given. Establish the x and y–intercept(s), critical numbers, possible points of inflection, increasing and decreasing intervals, and concave intervals. X-intercept(s): Y-intercept(s): Critical Numbers: Relative Max Relative Min Increasing Intervals: Decreasing Intervals: Points of Inflection: (Changes Concavity) Concave Up: 1/12/2022 5: 26 AM Concave Down: 3. 6 – Curve Sketching 8

EXAMPLE 2 The graph of function f(x) is given. Establish the x and y–intercept(s),

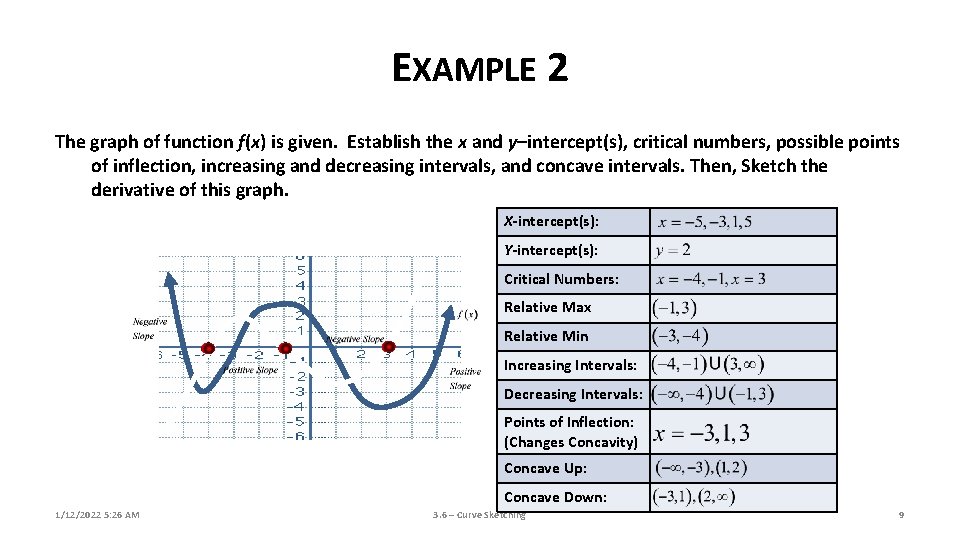
EXAMPLE 2 The graph of function f(x) is given. Establish the x and y–intercept(s), critical numbers, possible points of inflection, increasing and decreasing intervals, and concave intervals. Then, Sketch the derivative of this graph. X-intercept(s): Y-intercept(s): Critical Numbers: Relative Max Relative Min Increasing Intervals: Decreasing Intervals: Points of Inflection: (Changes Concavity) Concave Up: Concave Down: 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 9

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

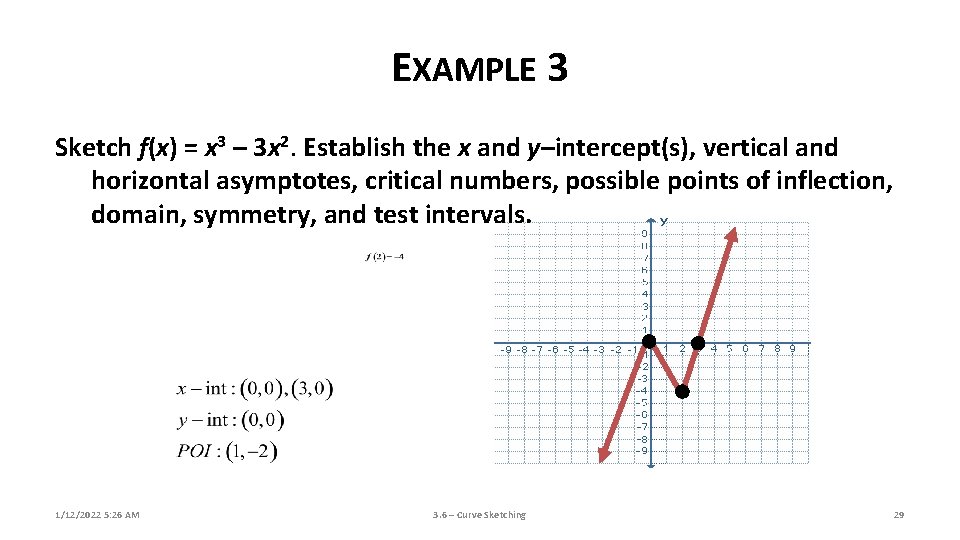
EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 10

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 11

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 12

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 13

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 14

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 15

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 16

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 17

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. x (–∞, 0) x=0 (0, 2) x=2 (2, ∞) f(x) f’(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 18

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (–∞, 0) 1/12/2022 5: 26 AM x=0 (0, 2) 3. 6 – Curve Sketching x=2 (2, ∞) 19

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (–∞, 0) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 20

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (0, 2) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 21

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (2, ∞) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 22

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. x (–∞, 0) x=0 (0, 2) x=2 (2, ∞) f(x) f’(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 23

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. x (–∞, 1) x=1 (1, ∞) f(x) f’’(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 24

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (–∞, 1) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 25

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. (1, ∞) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 26

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. x (–∞, 1) x=1 (1, ∞) f(x) f’’(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 27

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. x (–∞, 0) x=0 (0, 2) x=2 (2, ∞) f(x) f’(x) x (–∞, 1) x=1 (1, ∞) f(x) f’’(x) 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 28

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x

EXAMPLE 3 Sketch f(x) = x 3 – 3 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 29

EXAMPLE 4 Sketch f(x) = x 4 – 2 x 2. Establish the x

EXAMPLE 4 Sketch f(x) = x 4 – 2 x 2. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. X-intercept(s): Y-intercept(s): Critical Numbers: Relative Max Relative Min Increasing Intervals: Decreasing Intervals: Points of Inflection: (Changes Concavity) Concave Up: Concave Down: 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 30

YOUR TURN Sketch f(x) = 3 x 3 – 9 x + 1. Establish

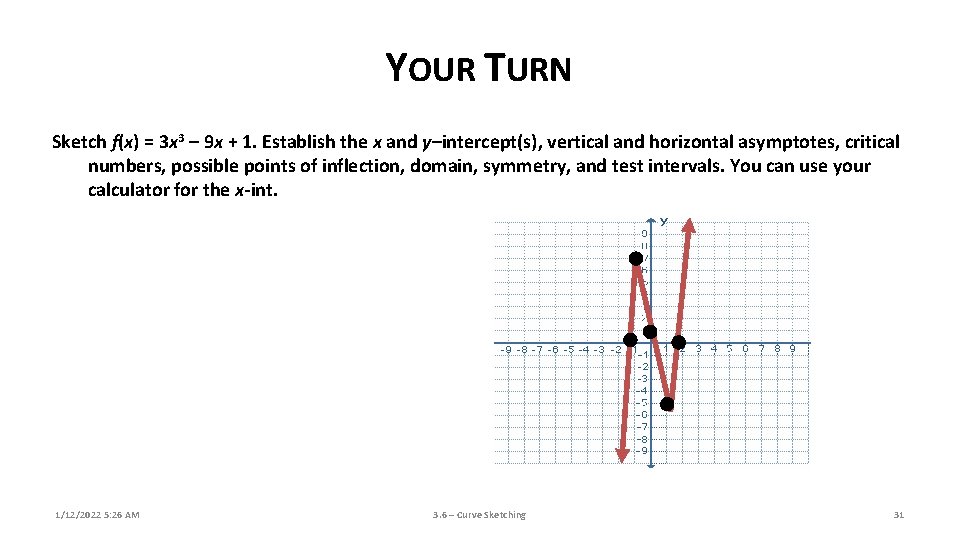
YOUR TURN Sketch f(x) = 3 x 3 – 9 x + 1. Establish the x and y–intercept(s), vertical and horizontal asymptotes, critical numbers, possible points of inflection, domain, symmetry, and test intervals. You can use your calculator for the x-int. 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 31

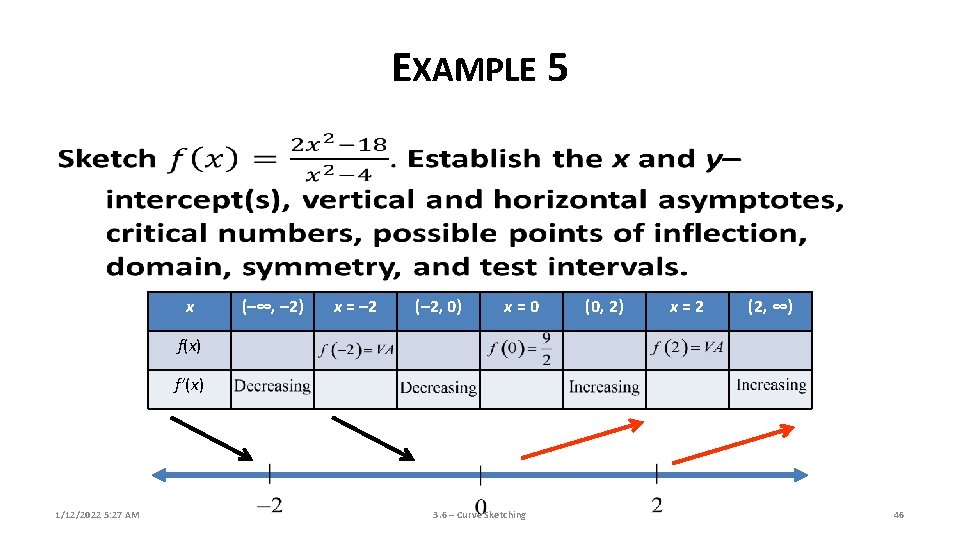
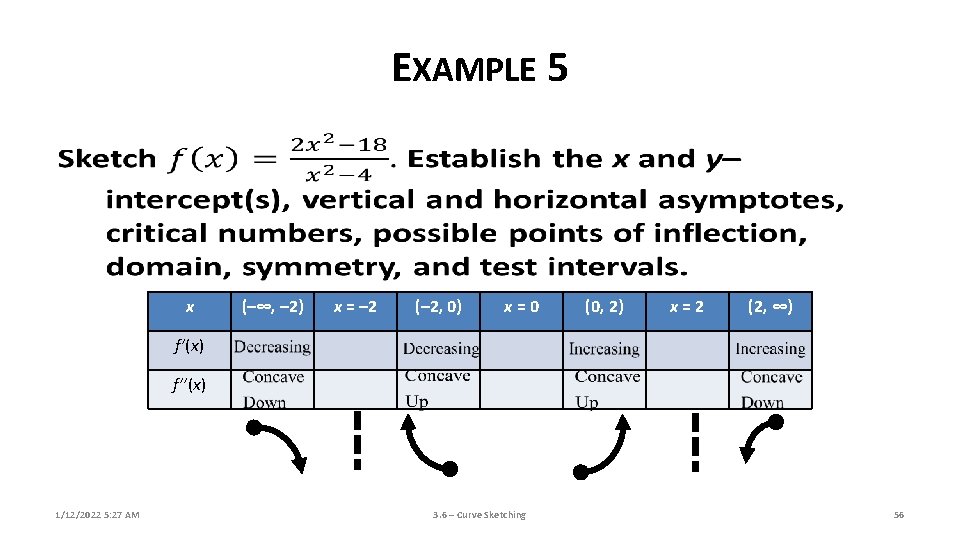
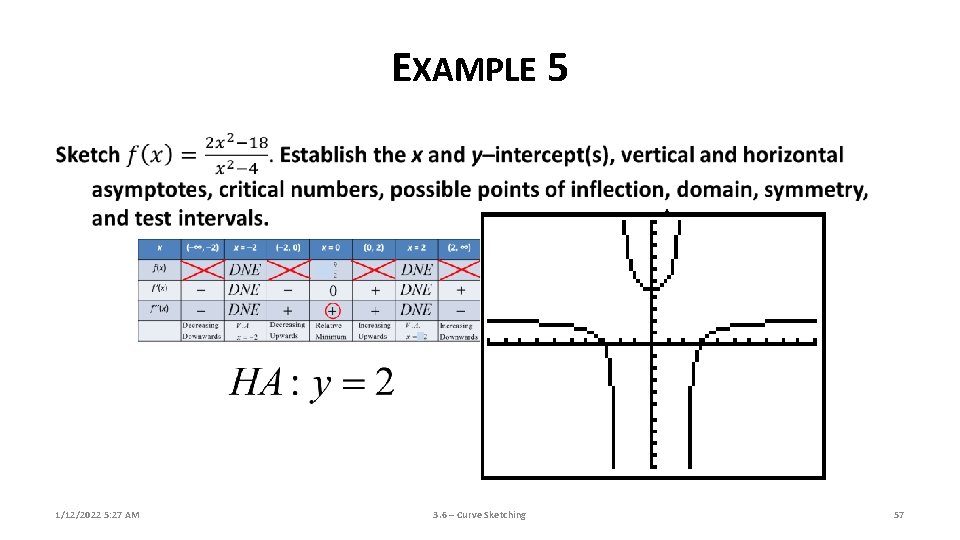
EXAMPLE 5 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 32

EXAMPLE 5 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 32

EXAMPLE 5 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 33

EXAMPLE 5 1/12/2022 5: 26 AM 3. 6 – Curve Sketching 33

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 34

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 34

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 35

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 35

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 36

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 36

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 37

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 37

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 38

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 38

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 39

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 39

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0 (0, 2) x=2 (2, ∞) f(x) f’(x) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 40

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM (– 2, 0) 3. 6

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM (– 2, 0) 3. 6 – Curve Sketching (0, 2) (2, ∞) 41

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 42

EXAMPLE 5 (– 2, 0) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching

EXAMPLE 5 (– 2, 0) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 43

EXAMPLE 5 (0, 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 44

EXAMPLE 5 (0, 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 44

EXAMPLE 5 (2, ∞) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 45

EXAMPLE 5 (2, ∞) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 45

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0 (0, 2) x=2 (2, ∞) f(x) f’(x) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 46

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 47

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 47

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 48

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 48

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 49

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 49

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 50

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 50

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0 (0, 2) x=2 (2, ∞) f’(x) f’’(x) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 51

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching

EXAMPLE 5 (–∞, – 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 52

EXAMPLE 5 (– 2, 0) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching

EXAMPLE 5 (– 2, 0) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 53

EXAMPLE 5 (0, 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 54

EXAMPLE 5 (0, 2) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 54

EXAMPLE 5 (2, ∞) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 55

EXAMPLE 5 (2, ∞) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 55

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0

EXAMPLE 5 x (–∞, – 2) x = – 2 (– 2, 0) x=0 (0, 2) x=2 (2, ∞) f’(x) f’’(x) 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 56

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 57

EXAMPLE 5 1/12/2022 5: 27 AM 3. 6 – Curve Sketching 57

YOUR TURN X-intercept(s): Y-intercept(s): Horizontal Asy. : Vertical Asymptote: Critical Numbers: Increasing Intervals: Decreasing

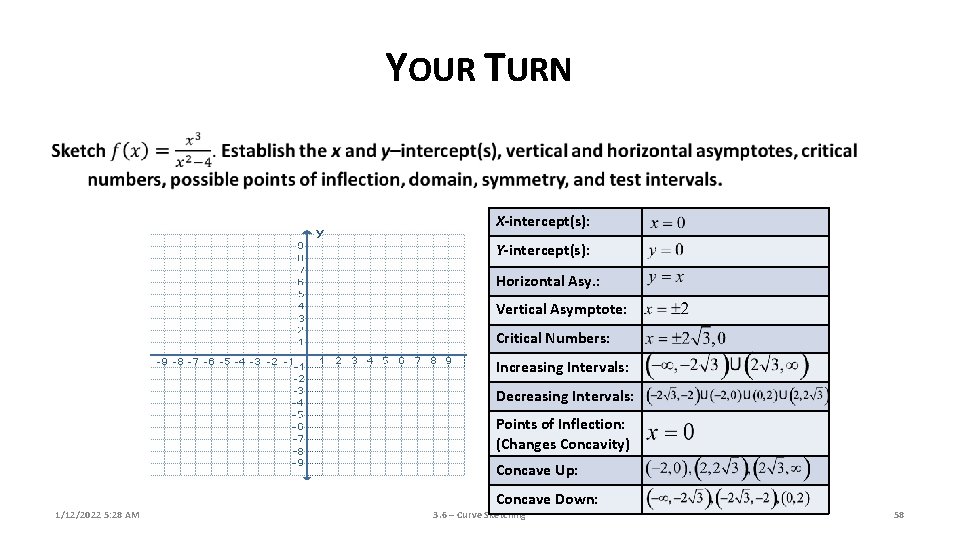
YOUR TURN X-intercept(s): Y-intercept(s): Horizontal Asy. : Vertical Asymptote: Critical Numbers: Increasing Intervals: Decreasing Intervals: Points of Inflection: (Changes Concavity) Concave Up: Concave Down: 1/12/2022 5: 28 AM 3. 6 – Curve Sketching 58

ASSIGNMENT Curve Sketching Worksheet 1/12/2022 5: 28 AM 3. 6 – Curve Sketching 59

ASSIGNMENT Curve Sketching Worksheet 1/12/2022 5: 28 AM 3. 6 – Curve Sketching 59