Curve Fitting with Exponential and Logarithmic Models How

Curve Fitting with Exponential and Logarithmic Models • How do we model data by using exponential and logarithmic functions? • How do we use exponential and logarithmic models to analyze and predict? Holt. Mc. Dougal Algebra 2 Holt

Curve Fitting with Exponential and Logarithmic Models In previous chapters, you used a graphing calculator to perform linear progressions and quadratic regressions to make predictions. You can also use an exponential model, which is an exponential function that represents a real data set. Once you know that data are exponential, you can use Exp. Reg (exponential regression) on your calculator to find a function that fits. This method of using data to find an exponential model is called an exponential regression. The calculator fits exponential functions to abx, so translations cannot be modeled. Holt Mc. Dougal Algebra 2

Curve Fitting with Exponential and Logarithmic Models Remember! If you do not see r 2 and r when you calculate regression, and turn these on by selecting Diagnostic. On. Holt Mc. Dougal Algebra 2

Curve Fitting with Exponential and Logarithmic Models College Application 1. Find an exponential model for the data. Use the model to predict when the tuition at U. T. Austin will be $6000. Step 1 Enter data into two lists in a graphing calculator. Use the exponential regression feature. An exponential model is f(x) ≈ 3236(1. 07 x), where f(x) represents the tuition and x is the number of years after the 1999– 2000 year. Holt Mc. Dougal Algebra 2 Tuition of the University of Texas Year Tuition 1999– 00 $3128 2000– 01 $3585 2001– 02 $3776 2002– 03 $3950 2003– 04 $4188

Curve Fitting with Exponential and Logarithmic Models College Application 1. Find an exponential model for the data. Use the model to predict when the tuition at U. T. Austin will be $6000. Step 2 Tuition of the University of Texas Graph the data and the function model to verify that it fits the data. Graph the line y = 6000 on Y 2. Zoom Out, then use 2 nd Trace (Calc) and hit Intersect The tuition will be about $6000 when t = 9 or 2008– 09. Holt Mc. Dougal Algebra 2 0 Year Tuition 1999– 00 $3128 2000– 01 $3585 2001– 02 $3776 2002– 03 $3950 2003– 04 $4188 7500 0 15

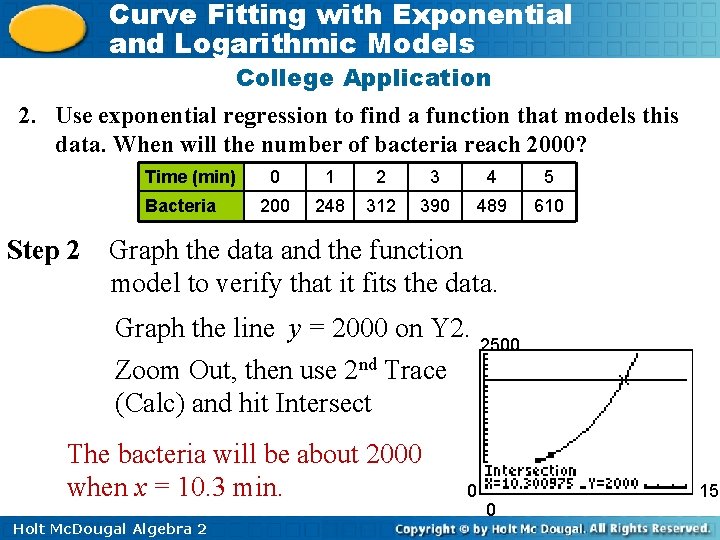
Curve Fitting with Exponential and Logarithmic Models College Application 2. Use exponential regression to find a function that models this data. When will the number of bacteria reach 2000? Time (min) Bacteria Step 1 0 1 2 3 4 5 200 248 312 390 489 610 Enter data into two lists in a graphing calculator. Use the exponential regression feature. An exponential model is f(x) ≈ 199(1. 25 x), where f(x) represents the number of bacteria and x is the number of minutes. Holt Mc. Dougal Algebra 2

Curve Fitting with Exponential and Logarithmic Models College Application 2. Use exponential regression to find a function that models this data. When will the number of bacteria reach 2000? Time (min) Bacteria Step 2 0 1 2 3 4 5 200 248 312 390 489 610 Graph the data and the function model to verify that it fits the data. Graph the line y = 2000 on Y 2. Zoom Out, then use 2 nd Trace (Calc) and hit Intersect The bacteria will be about 2000 when x = 10. 3 min. Holt Mc. Dougal Algebra 2 0 2500 0 15

Curve Fitting with Exponential and Logarithmic Models Many natural phenomena can be modeled by natural log functions. You can use a logarithmic regression to find a function Helpful Hint Most calculators that perform logarithmic regression use ln rather than log. Holt Mc. Dougal Algebra 2

Curve Fitting with Exponential and Logarithmic Models Application 3. Find a natural log model for the data. According to the model, when will the global population exceed 9, 000, 000? Step 1 Enter data into two lists in a graphing calculator. Use the logarithmic regression feature. An logarithmic model is f(x) ≈ 1824 + 106 ln x, where f(x) is the year and x is the population in billions. Holt Mc. Dougal Algebra 2 Global Population Growth Populatio n (billions) Year 1 1800 2 1927 3 1960 4 1974 5 1987 6 1999

Curve Fitting with Exponential and Logarithmic Models Application Global Population Growth 3. Find a natural log model for the data. According to the model, when will the global population exceed 9, 000, 000? Step 2 Populatio n (billions) Year 1 1800 2 1927 3 1960 4 1974 5 1987 6 1999 Graph the data and the function model to verify that it fits the data. Because we are looking for the y -value when x = 9, you can use the table and scroll down to x = 9. The population will exceed 9, 000, 000 in the year 2057. Holt Mc. Dougal Algebra 2 0 2500 15 0

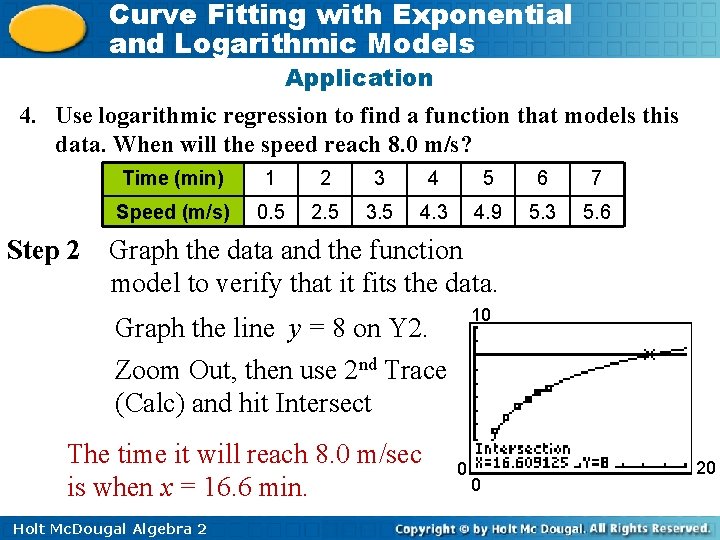
Curve Fitting with Exponential and Logarithmic Models Application 4. Use logarithmic regression to find a function that models this data. When will the speed reach 8. 0 m/s? Step 1 Time (min) 1 2 3 4 5 6 7 Speed (m/s) 0. 5 2. 5 3. 5 4. 3 4. 9 5. 3 5. 6 Enter data into two lists in a graphing calculator. Use the logarithmic regression feature. An logarithmic model is f(x) ≈ 0. 59 + 2. 64 ln x, where f(x) is the time and x is the speed. Holt Mc. Dougal Algebra 2

Curve Fitting with Exponential and Logarithmic Models Application 4. Use logarithmic regression to find a function that models this data. When will the speed reach 8. 0 m/s? Step 2 Time (min) 1 2 3 4 5 6 7 Speed (m/s) 0. 5 2. 5 3. 5 4. 3 4. 9 5. 3 5. 6 Graph the data and the function model to verify that it fits the data. 10 Graph the line y = 8 on Y 2. Zoom Out, then use 2 nd Trace (Calc) and hit Intersect The time it will reach 8. 0 m/sec is when x = 16. 6 min. Holt Mc. Dougal Algebra 2 0 0 20

Curve Fitting with Exponential and Logarithmic Models Lesson 15. 2 Practice B Holt Mc. Dougal Algebra 2