Curve Fitting with Curving Fitting 6 9 Polynomial

Curve Fitting with Curving Fitting 6 -9 Polynomial Functions Warm Up Lesson Presentation Lesson Quiz Holt Mc. Dougal Algebra 2 Algebra 22 Holt Mc. Dougal

6 -9 Curve Fitting with Polynomial Functions Warm Up Find a line of best fit for the data. 1. x y 2 70 8 62 15 80 21 190 24 160 y = 5. 45 x + 36. 12 2. x y 38 92 42 80 44 75 35 81 49 68 y = – 1. 28 x + 132. 66 Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Objectives Use finite differences to determine the degree of a polynomial that will fit a given set of data. Use technology to find polynomial models for a given set of data. Holt Mc. Dougal Algebra 2

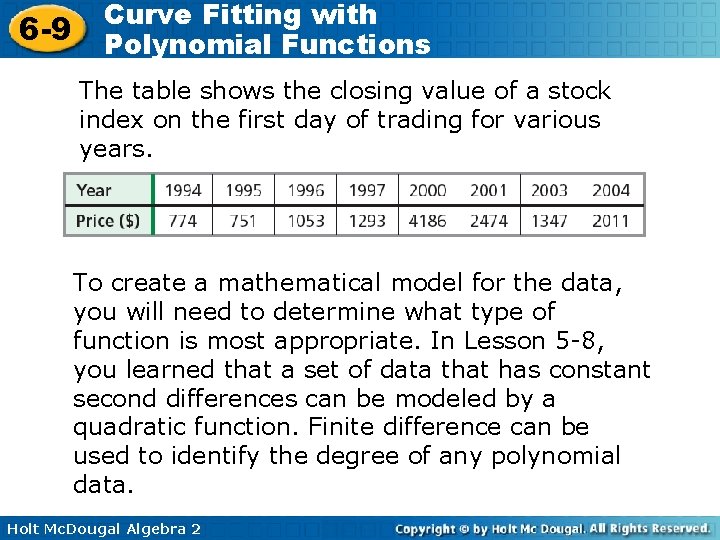
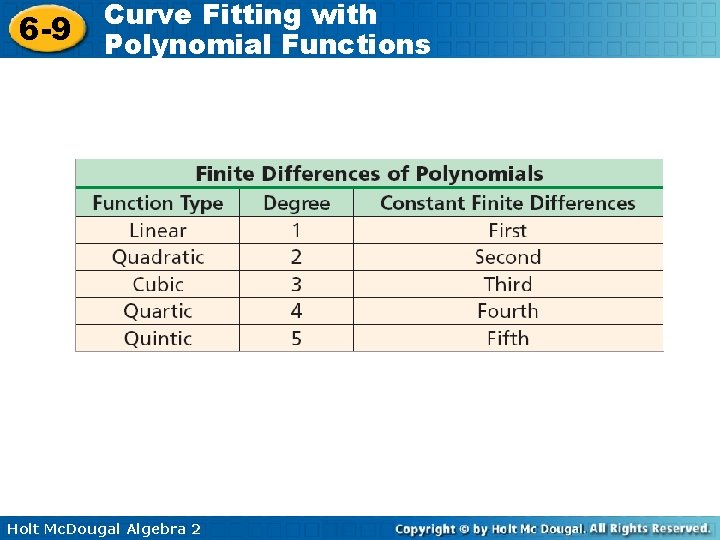
6 -9 Curve Fitting with Polynomial Functions The table shows the closing value of a stock index on the first day of trading for various years. To create a mathematical model for the data, you will need to determine what type of function is most appropriate. In Lesson 5 -8, you learned that a set of data that has constant second differences can be modeled by a quadratic function. Finite difference can be used to identify the degree of any polynomial data. Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Holt Mc. Dougal Algebra 2

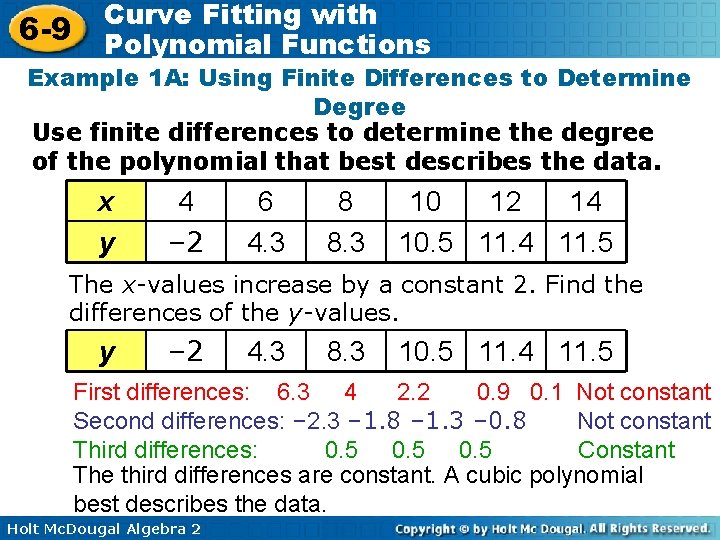
6 -9 Curve Fitting with Polynomial Functions Example 1 A: Using Finite Differences to Determine Degree Use finite differences to determine the degree of the polynomial that best describes the data. x y 4 – 2 6 4. 3 8 8. 3 10 12 14 10. 5 11. 4 11. 5 The x-values increase by a constant 2. Find the differences of the y-values. y – 2 4. 3 8. 3 10. 5 11. 4 11. 5 First differences: 6. 3 4 2. 2 0. 9 0. 1 Not constant Second differences: – 2. 3 – 1. 8 – 1. 3 – 0. 8 Not constant Third differences: 0. 5 Constant The third differences are constant. A cubic polynomial best describes the data. Holt Mc. Dougal Algebra 2

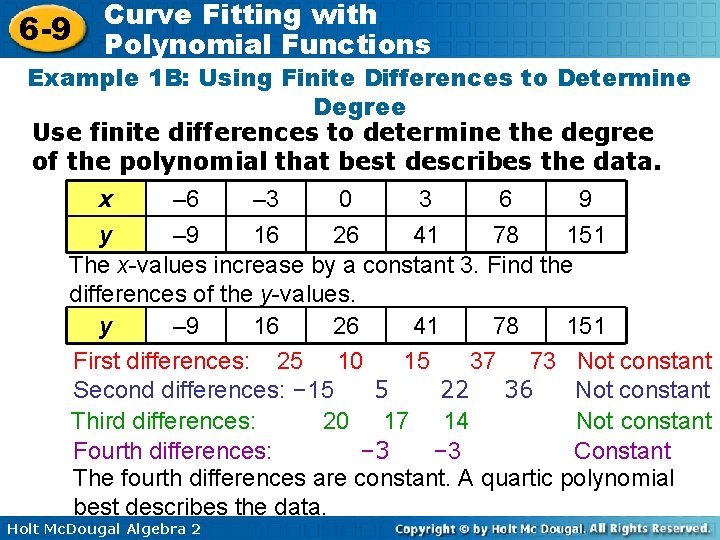
6 -9 Curve Fitting with Polynomial Functions Example 1 B: Using Finite Differences to Determine Degree Use finite differences to determine the degree of the polynomial that best describes the data. x – 6 – 3 0 3 6 9 y – 9 16 26 41 78 151 The x-values increase by a constant 3. Find the differences of the y-values. y – 9 16 26 41 78 151 First differences: 25 10 15 37 73 Not constant Second differences: – 15 5 22 36 Not constant Third differences: 20 17 14 Not constant Fourth differences: – 3 Constant The fourth differences are constant. A quartic polynomial best describes the data. Holt Mc. Dougal Algebra 2

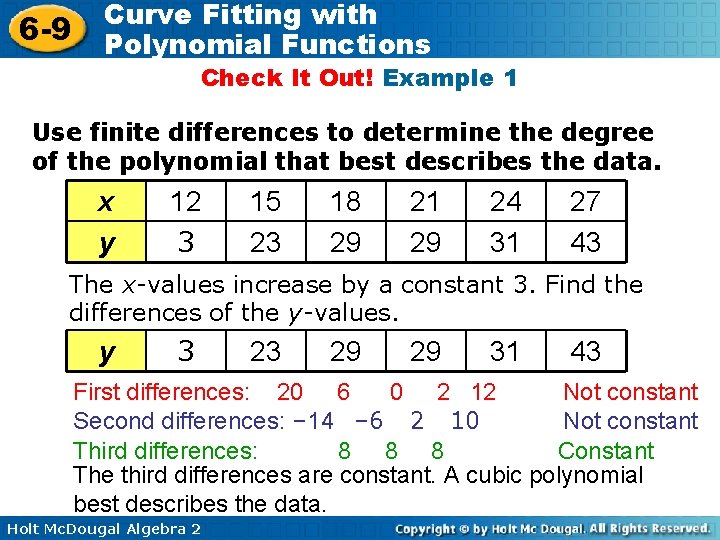
6 -9 Curve Fitting with Polynomial Functions Check It Out! Example 1 Use finite differences to determine the degree of the polynomial that best describes the data. x y 12 3 15 23 18 29 21 29 24 31 27 43 The x-values increase by a constant 3. Find the differences of the y-values. y 3 23 29 29 31 43 First differences: 20 6 0 2 12 Not constant Second differences: – 14 – 6 2 10 Not constant Third differences: 8 8 8 Constant The third differences are constant. A cubic polynomial best describes the data. Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Once you have determined the degree of the polynomial that best describes the data, you can use your calculator to create the function. Holt Mc. Dougal Algebra 2

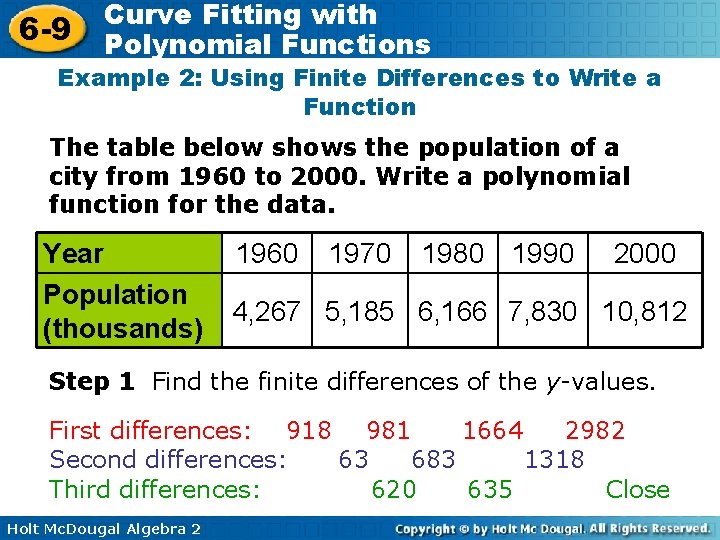
6 -9 Curve Fitting with Polynomial Functions Example 2: Using Finite Differences to Write a Function The table below shows the population of a city from 1960 to 2000. Write a polynomial function for the data. Year Population (thousands) 1960 1970 1980 1990 2000 4, 267 5, 185 6, 166 7, 830 10, 812 Step 1 Find the finite differences of the y-values. First differences: 918 981 1664 2982 Second differences: 63 683 1318 Third differences: 620 635 Close Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Example 2 Continued Step 2 Determine the degree of the polynomial. Because third differences are relatively close, a cubic function should be a good model. Step 3 Use the cubic regression feature on your calculator. f(x) ≈ 0. 10 x 3 – 2. 84 x 2 + 109. 84 x + 4266. 79 Holt Mc. Dougal Algebra 2

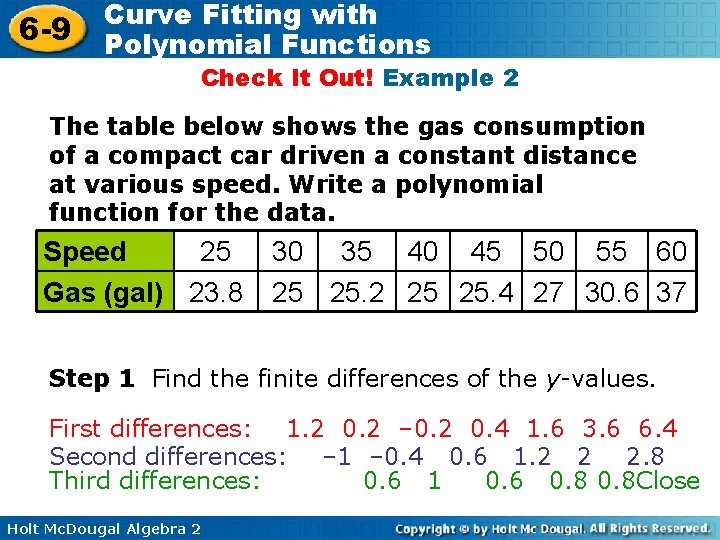
6 -9 Curve Fitting with Polynomial Functions Check It Out! Example 2 The table below shows the gas consumption of a compact car driven a constant distance at various speed. Write a polynomial function for the data. Speed 25 Gas (gal) 23. 8 30 35 40 45 50 55 60 25 25. 2 25 25. 4 27 30. 6 37 Step 1 Find the finite differences of the y-values. First differences: 1. 2 0. 2 – 0. 2 0. 4 1. 6 3. 6 6. 4 Second differences: – 1 – 0. 4 0. 6 1. 2 2 2. 8 Third differences: 0. 6 1 0. 6 0. 8 Close Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Check It Out! Example 2 Continued Step 2 Determine the degree of the polynomial. Because third differences are relatively close, a cubic function should be a good model. Step 3 Use the cubic regression feature on your calculator. f(x) ≈ 0. 001 x 3 – 0. 113 x 2 + 4. 134 x + 24. 867 Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Often, real-world data can be too irregular for you to use finite differences or find a polynomial function that fits perfectly. In these situations, you can use the regression feature of your graphing calculator. Remember that the closer the R 2 -value is to 1, the better the function fits the data. Holt Mc. Dougal Algebra 2

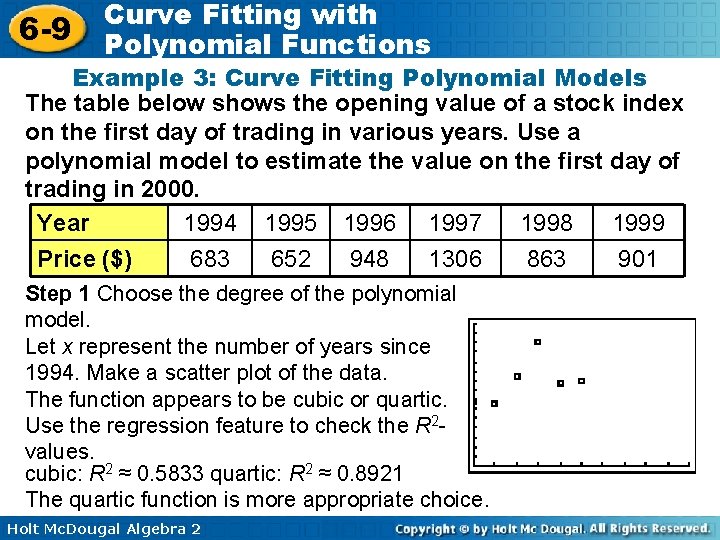
6 -9 Curve Fitting with Polynomial Functions Example 3: Curve Fitting Polynomial Models The table below shows the opening value of a stock index on the first day of trading in various years. Use a polynomial model to estimate the value on the first day of trading in 2000. Year 1994 1995 1996 1997 1998 1999 Price ($) 683 652 948 1306 863 901 Step 1 Choose the degree of the polynomial model. Let x represent the number of years since 1994. Make a scatter plot of the data. The function appears to be cubic or quartic. Use the regression feature to check the R 2 values. cubic: R 2 ≈ 0. 5833 quartic: R 2 ≈ 0. 8921 The quartic function is more appropriate choice. Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Example 3 Continued Step 2 Write the polynomial model. The data can be modeled by f(x) = 32. 23 x 4 – 339. 13 x 3 + 1069. 59 x 2 – 858. 99 x + 693. 88 Step 3 Find the value of the model corresponding to 2000 is 6 years after 1994. Substitute 6 for x in the quartic model. f(6) = 32. 23(6)4 – 339. 13(6)3 + 1069. 59(6)2 – 858. 99(6) + 693. 88 Based on the model, the opening value was about $2563. 18 in 2000. Holt Mc. Dougal Algebra 2

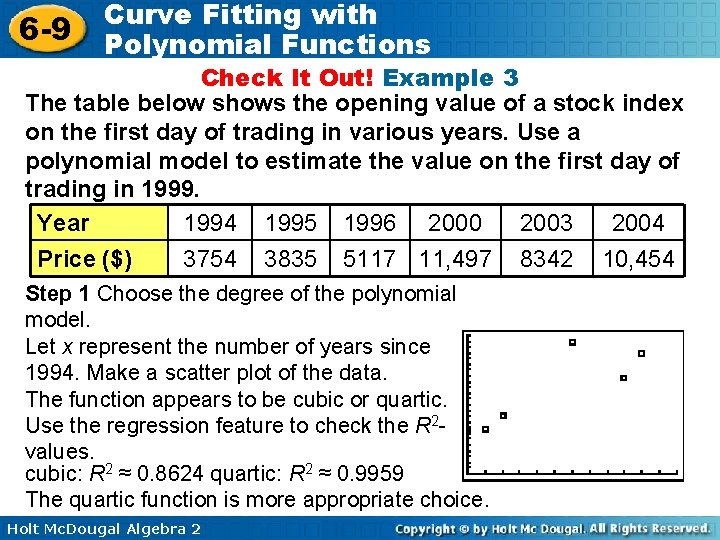
6 -9 Curve Fitting with Polynomial Functions Check It Out! Example 3 The table below shows the opening value of a stock index on the first day of trading in various years. Use a polynomial model to estimate the value on the first day of trading in 1999. Year 1994 1995 1996 2000 2003 2004 Price ($) 3754 3835 5117 11, 497 8342 10, 454 Step 1 Choose the degree of the polynomial model. Let x represent the number of years since 1994. Make a scatter plot of the data. The function appears to be cubic or quartic. Use the regression feature to check the R 2 values. cubic: R 2 ≈ 0. 8624 quartic: R 2 ≈ 0. 9959 The quartic function is more appropriate choice. Holt Mc. Dougal Algebra 2

6 -9 Curve Fitting with Polynomial Functions Check It Out! Example 3 Continued Step 2 Write the polynomial model. The data can be modeled by f(x) = 19. 09 x 4 – 377. 90 x 3 + 2153. 24 x 2 – 2183. 29 x + 3871. 46 Step 3 Find the value of the model corresponding to 1999 is 5 years after 1994. Substitute 5 for x in the quartic model. f(5) = 19. 09(5)4 – 377. 90(5)3 + 2153. 24(5)2 – 2183. 29(5) + 3871. 46 Based on the model, the opening value was about $11, 479. 76 in 1999. Holt Mc. Dougal Algebra 2

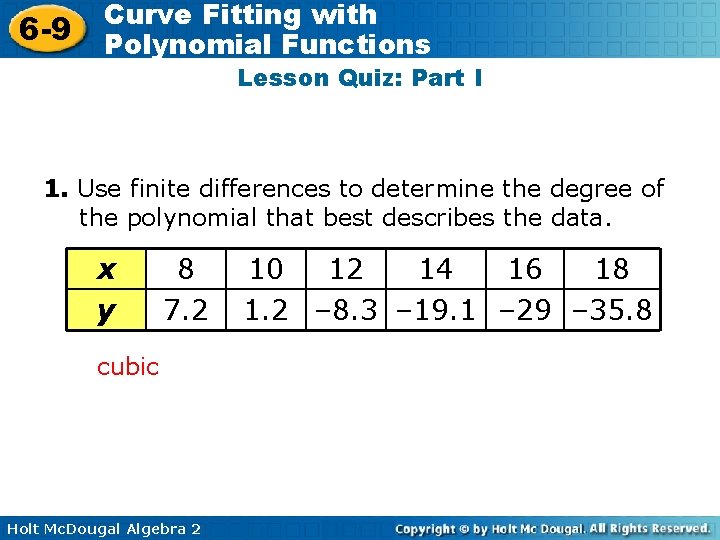
6 -9 Curve Fitting with Polynomial Functions Lesson Quiz: Part I 1. Use finite differences to determine the degree of the polynomial that best describes the data. x y 8 7. 2 cubic Holt Mc. Dougal Algebra 2 10 12 14 16 18 1. 2 – 8. 3 – 19. 1 – 29 – 35. 8

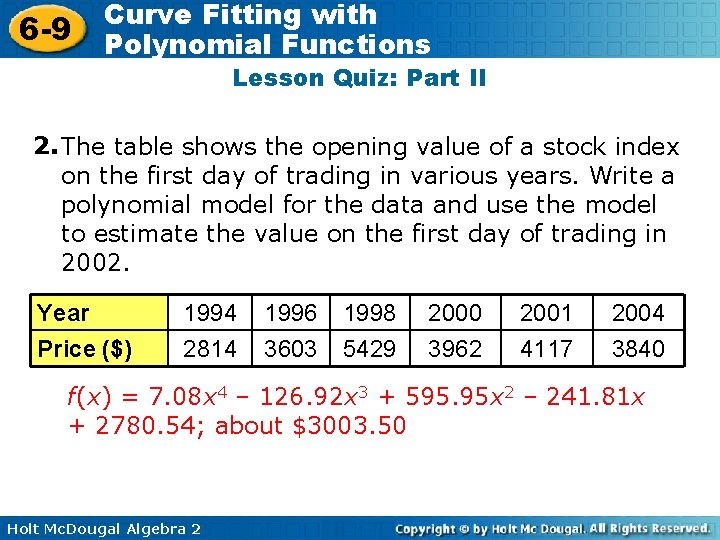
6 -9 Curve Fitting with Polynomial Functions Lesson Quiz: Part II 2. The table shows the opening value of a stock index on the first day of trading in various years. Write a polynomial model for the data and use the model to estimate the value on the first day of trading in 2002. Year Price ($) 1994 2814 1996 3603 1998 5429 2000 3962 2001 4117 2004 3840 f(x) = 7. 08 x 4 – 126. 92 x 3 + 595. 95 x 2 – 241. 81 x + 2780. 54; about $3003. 50 Holt Mc. Dougal Algebra 2