Curvature Motion for Union of Balls Thomas Lewiner

Curvature Motion for Union of Balls Thomas Lewiner♥♠, Cynthia Ferreira♥, Marcos Craizer♥ and Ralph Teixeira♣ ♥ Department of Mathematics — PUC-Rio ♠ Géométrica Project — INRIA Sophia Antipolis ♣ FGV -Rio

Morphological Motions T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 2

Expected Properties of Motion n n No self-intersection No singularities No disconnection Convexification Simplification Curvature Motion T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 3

Curvature Motion @Q ( s; t ) @t = K (s; t) ¢N (s; t) T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 4

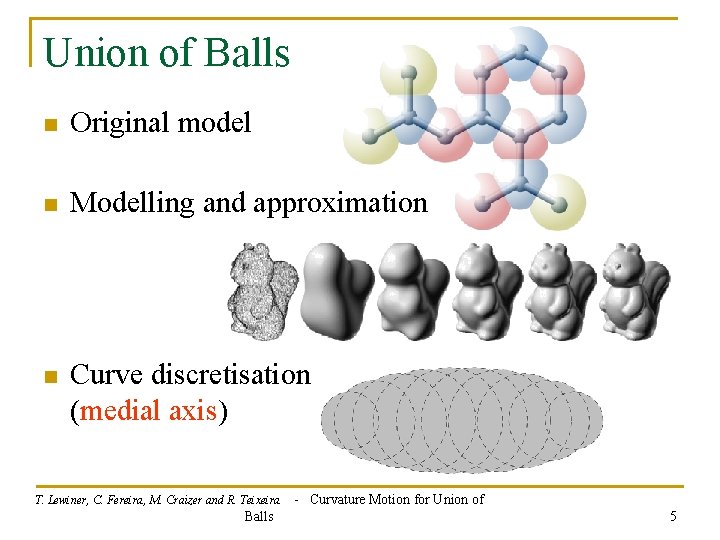
Union of Balls n Original model n Modelling and approximation n Curve discretisation (medial axis) T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 5

Contributions n n n Explicit curvature motion for union of balls Sampling conditions on the union of balls Derivative approximations for the union of balls T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 6

Summary n n n Medial Axis Curvature Motion from the Medial Axis Curvature Motion for Union of Balls Implementation Issues Results T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 7

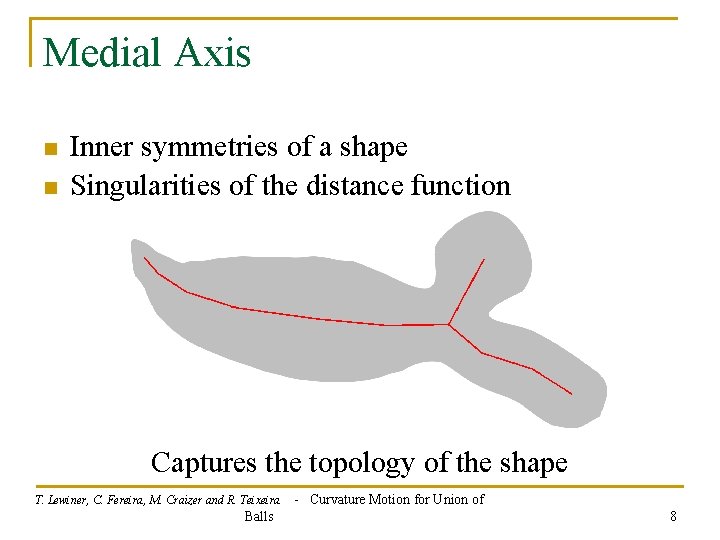
Medial Axis n n Inner symmetries of a shape Singularities of the distance function Captures the topology of the shape T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 8

Medial Axis of a Union of Balls Classical Algorithmic Geometry (Amenta et al. , CGTA 2001) Medial axis inside the alpha-shape - Curvature Motion for Union of T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls 9

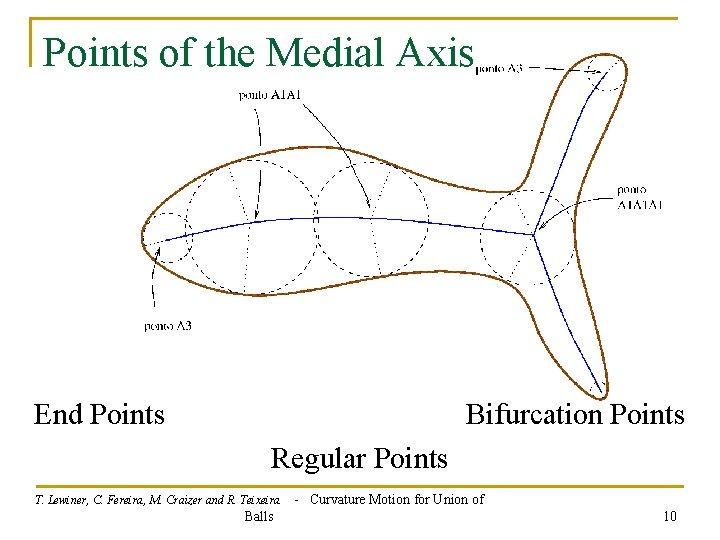
Points of the Medial Axis End Points Bifurcation Points Regular Points T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 10

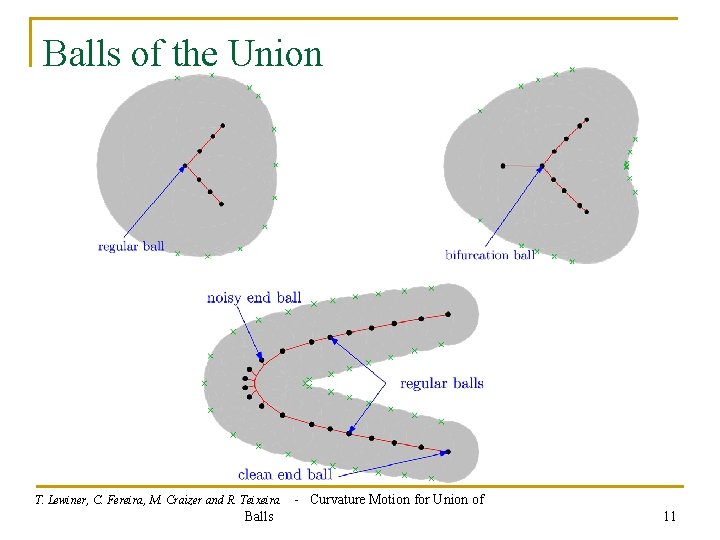
Balls of the Union T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 11

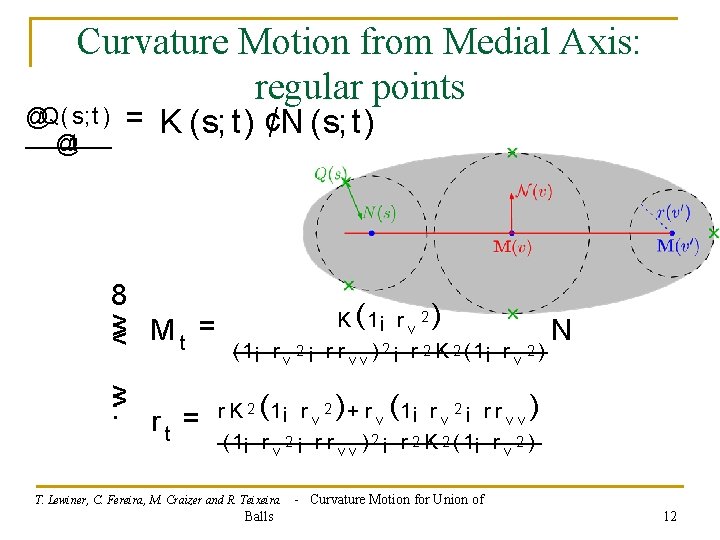
Curvature Motion from Medial Axis: regular points @Q ( s; t ) @t = K (s; t) ¢N (s; t) 8 > > < Mt = > > : r = t K ( 1¡ r v 2 ) N 2 ( 1¡ r v 2 ¡ r r v v ) ¡ r 2 K 2 ( 1¡ r v 2 ) r K 2 ( 1¡ r v 2 ) + r v ( 1¡ r v 2 ¡ r r v v ) 2 ¡ r 2 K 2 ( 1¡ r v 2 ) T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 12

8 > > < Mt = Regular balls > > : r = t K ( 1¡ r v 2 ) N (1¡ r v 2 ¡ r r v v ) 2 ¡ r 2 K 2 (1¡ r v 2 ) r K 2 ( 1¡ r v 2 ) + r v ( 1¡ r v 2 ¡ r r v v ) (1¡ r v 2 ¡ r r v v ) 2 ¡ r 2 K 2 (1¡ r v 2 ) 1 st and 2 nd derivatives on the medial axis: ) [Lewiner et al. , Sibgrapi 2004] T ; N ; K ; r vv T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 13

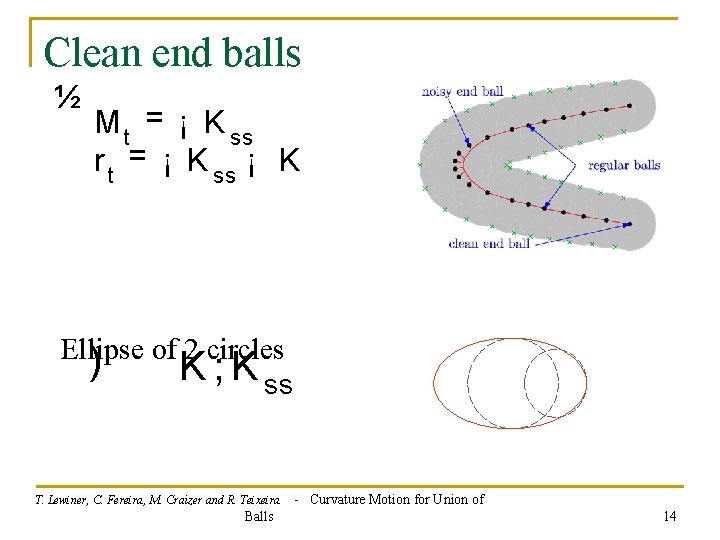
Clean end balls ½ M t = ¡ K ss r t = ¡ K ss ¡ K Ellipse of 2 circles ) K ; K ss T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 14

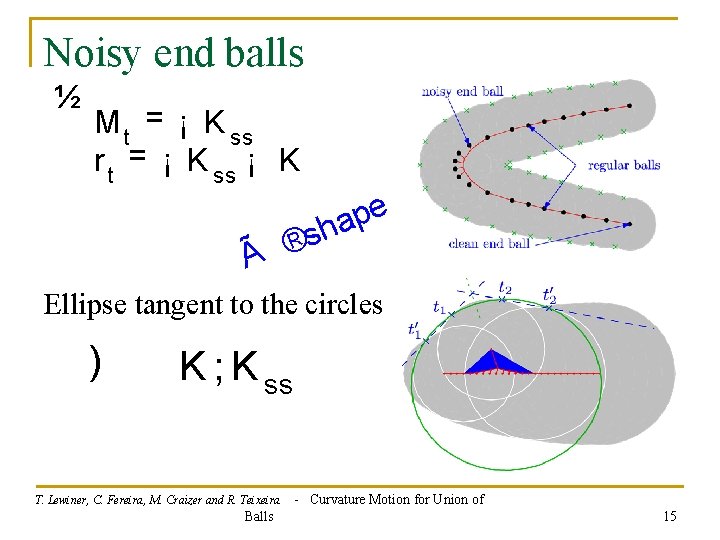
Noisy end balls ½ M t = ¡ K ss r t = ¡ K ss ¡ K e p a h s à ® Ellipse tangent to the circles ) K ; K ss T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 15

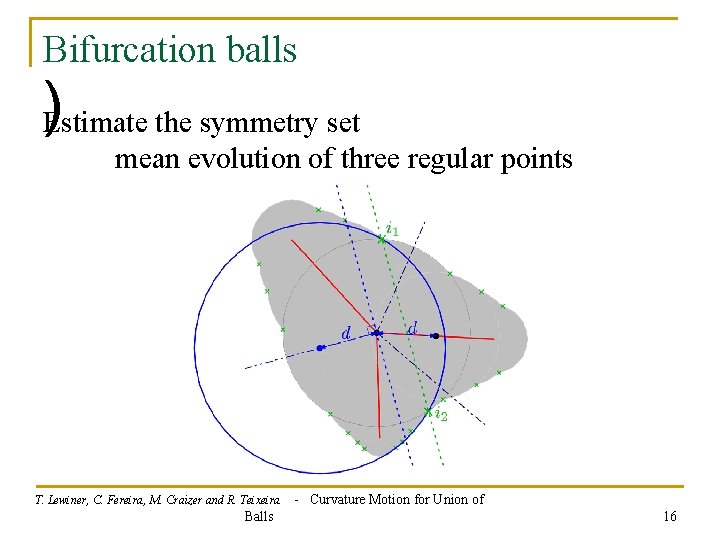
Bifurcation balls )Estimate the symmetry set mean evolution of three regular points T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 16

Sampling Conditions 1 min(r; r 0) · kc ¡ c 0 k · min(r; r 0) 20 Adjacent B (c; rballs: ) B (c 0; r 0) n Over-sampling (rarefaction) : add. Bball ( c+ c 0 ; r + r ) 2 n 2 Sub-sampling (numerical) : replace c+ c 0 by B ( balls ; r+r ) 2 2 T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 17

Numerical Issues n n Inner balls $ Bifurcation regular topological change Avoiding non-existent holes Numerical validation : fallback to end ball case T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 18

Comparison with Megawave [Craizer et al. , Math Imaging & Vision, 2004] T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 19

Reaction-Diffusion Scale-Space Qt (s; t) = (® + ¯K (s; t)) N (s; t) T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 20

Future works: 3 D? T. Lewiner, C. Fereira, M. Craizer and R. Teixeira Balls - Curvature Motion for Union of 21

Thank you!