CURS METODE NEDISTRUCTIVE SIMETRIE DIFRACIA RX 1 Simetrie

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 1. Simetrie, difracţie de raze X 1

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX TRANSLAŢIE 2

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 3

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX ROTAŢIE 4

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 5

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 6

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 7

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX REFLEXIE 8

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 9

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 10

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX INVERSIE 11

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 12

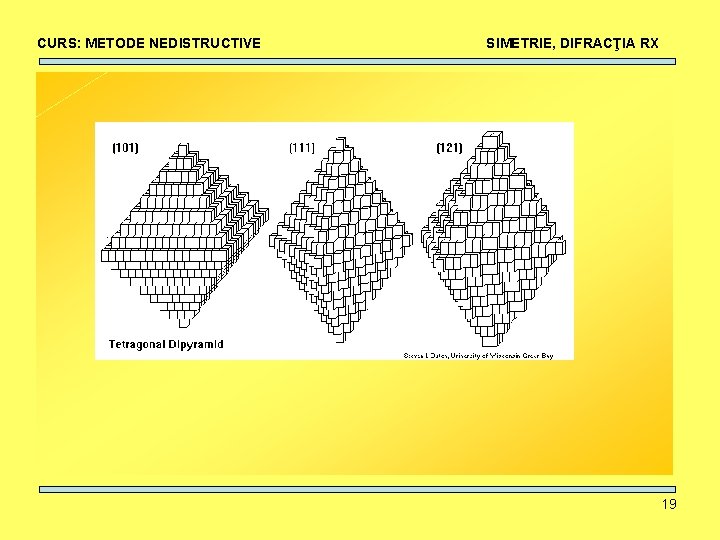
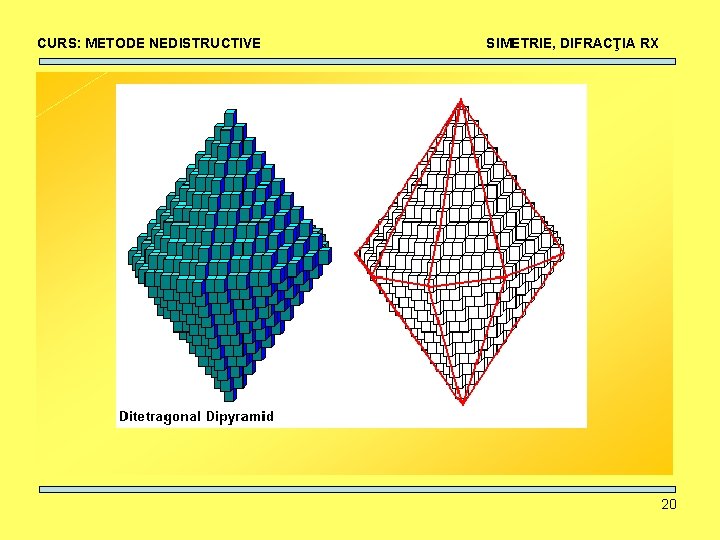
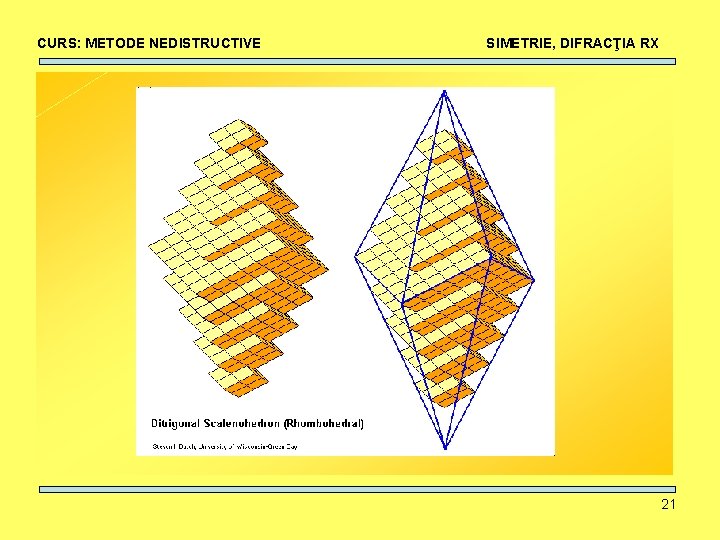
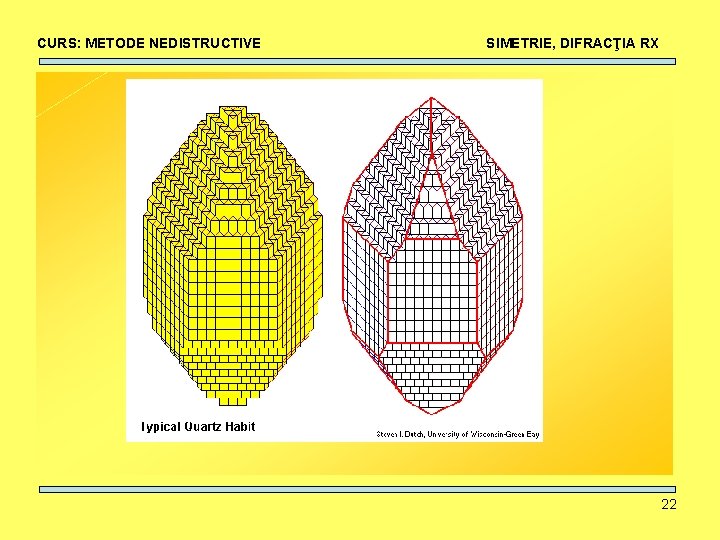
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX ÎN NATURĂ 13

CURS: METODE NEDISTRUCTIVE Rutile SIMETRIE, DIFRACŢIA RX Amethyst Batnasite/dolomite 14

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Pyrite Almandin ALMANDIN Beryl 15

CURS: METODE NEDISTRUCTIVE Calcite SIMETRIE, DIFRACŢIA RX Beryl GRAPHITE Gmelinit 16

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX CUM SE FORMEAZĂ? 17

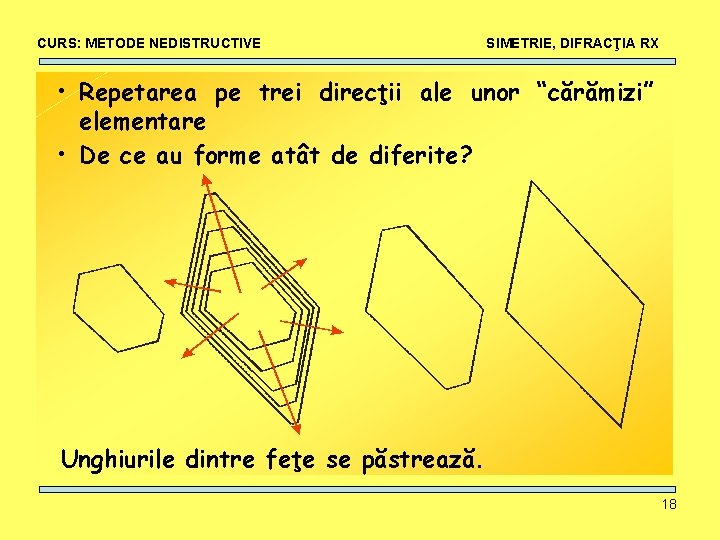
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX • Repetarea pe trei direcţii ale unor “cărămizi” elementare • De ce au forme atât de diferite? Unghiurile dintre feţe se păstrează. 18

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 19

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 20

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 21

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 22

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 23

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX • Într-un cristal “bine format” toate feţele care sunt legate între ele prin operaţii de simetrie sunt dezvoltate identic. • Accidentele de cristalizare nu afectează unghiurile dintre feţe ci doar mărimea lor relativă. F + C = M + 2 • Monocristal, policristal, amorf • Cristal ideal 24

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Solidul cristalin • • Structura atomică a monocristalului se repetă în întreg volumul cristalului. Repetarea – prin translaţie pe trei axe. Monocristal pirită Solid amorf Monocristal 25

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Solidul policristalin 26

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Solidul amorf • • • Format din atomi, ioni sau molecule care nu au o aranjare ordonată. Există ordine la mică distanţă (câteva dimensiuni atomice sau moleculare). Ex: siliciu amorf (folosit în fabricarea celulelor solare, . . . ). 27

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemplu 2 D: 28

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţeaua cristalină este o repetare regulată pe trei direcţii necoplanare din spaţiu a unor puncte echivalente numite noduri ale reţelei de unde vecinătatea atomică observată este aceeaşi. 29

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX • Alegerea primului punct este arbitrară. • Celelalte trebuie să satisfacă condiţia de vecinătate structura cristalină = reţea + bază reţea identică, bază identică. Ce diferă? 30

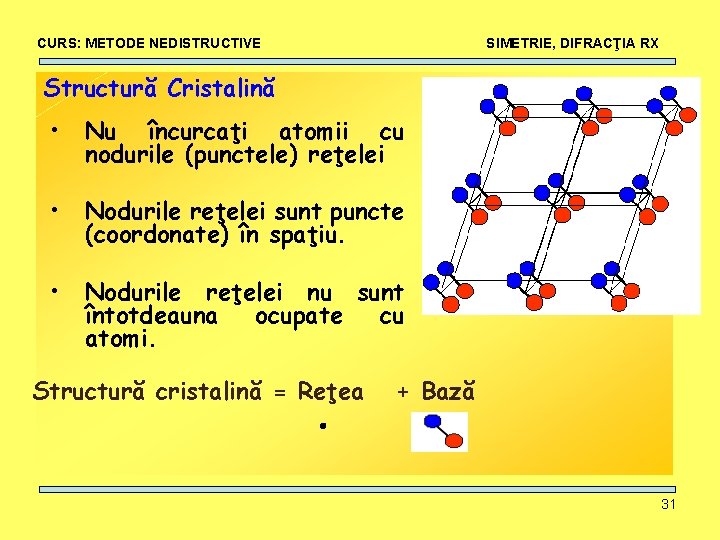
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Structură Cristalină • Nu încurcaţi atomii cu nodurile (punctele) reţelei • Nodurile reţelei sunt puncte (coordonate) în spaţiu. • Nodurile reţelei nu sunt întotdeauna ocupate cu atomi. Structură cristalină = Reţea + Bază 31

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX CELULA ELEMENTARĂ, CELULA PRIMITIVĂ Celulă elementară: unitate care prin repetare generează întreaga reţea. Se alege astfel încât să conţină elementele de simetrie în colţuri sau pe muchii. Celula elementară umple spaţiul prin translaţie. Celulă primitivă: are un singur nod pe celulă. Numărul de noduri: N 2 D = (1/4)Nc + NI N 3 D = (1/8)Nc + (1/2)Nf + NI La fel se calculează şi numărul de atomi/celula elementară ( + (1/2)Nm în 2 D, + (1/4)Nm în 3 D). 32

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 33

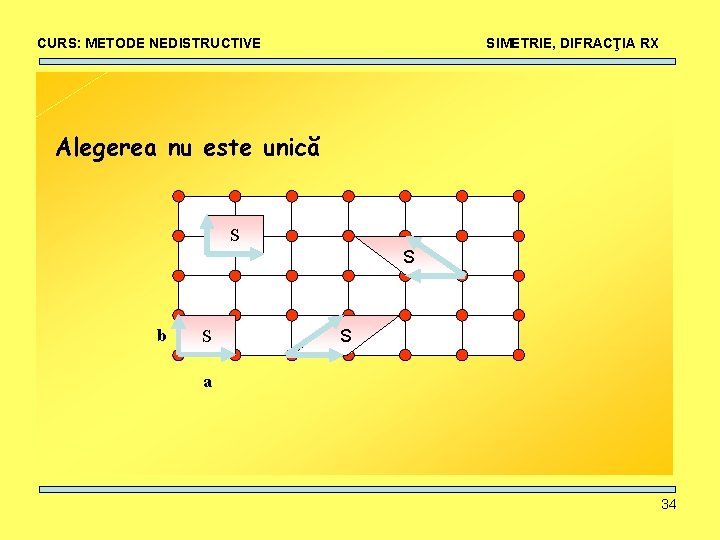
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Alegerea nu este unică S S b S S a 34

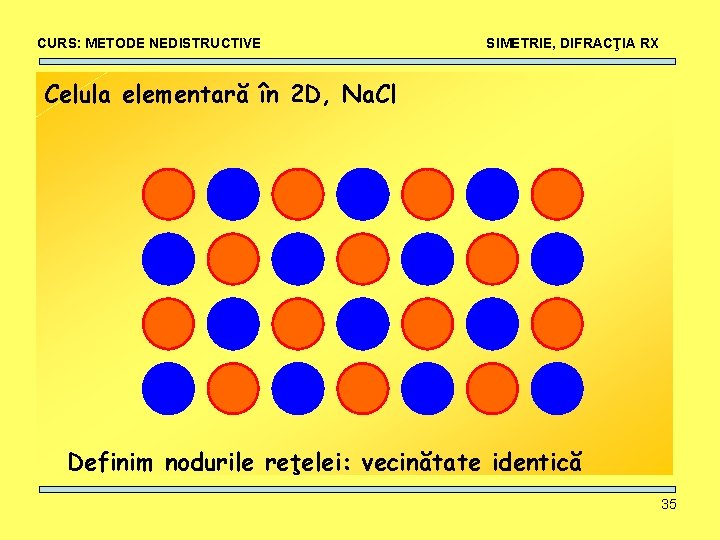
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Celula elementară în 2 D, Na. Cl Definim nodurile reţelei: vecinătate identică 35

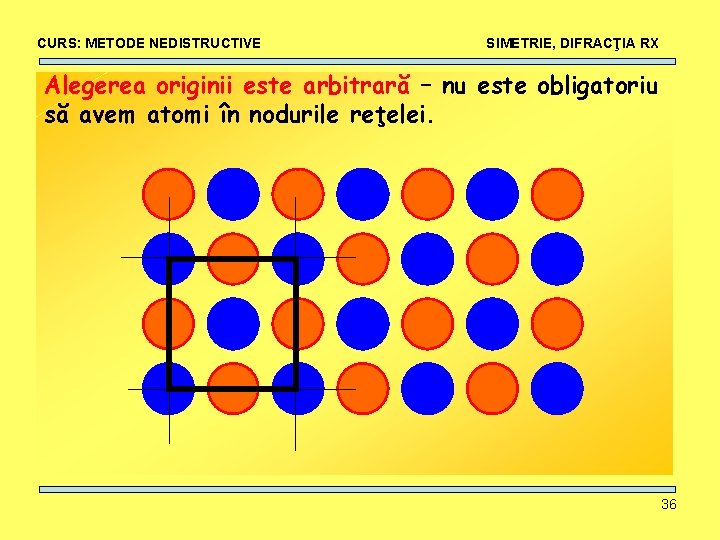
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Alegerea originii este arbitrară – nu este obligatoriu să avem atomi în nodurile reţelei. 36

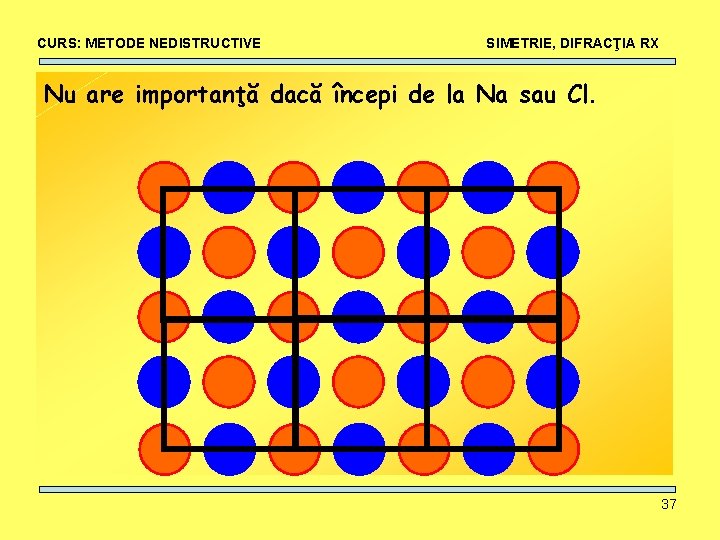
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Nu are importanţă dacă începi de la Na sau Cl. 37

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX - sau dacă nu porneşti de la un atom 38

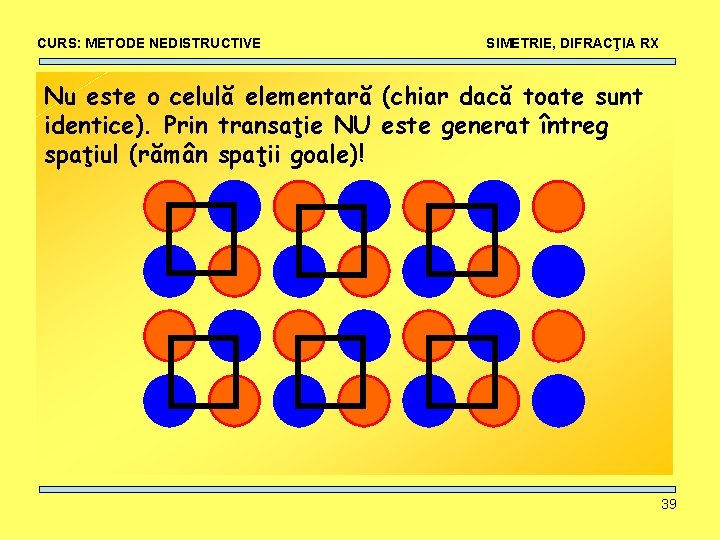
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Nu este o celulă elementară (chiar dacă toate sunt identice). Prin transaţie NU este generat întreg spaţiul (rămân spaţii goale)! 39

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Sau. . . 40

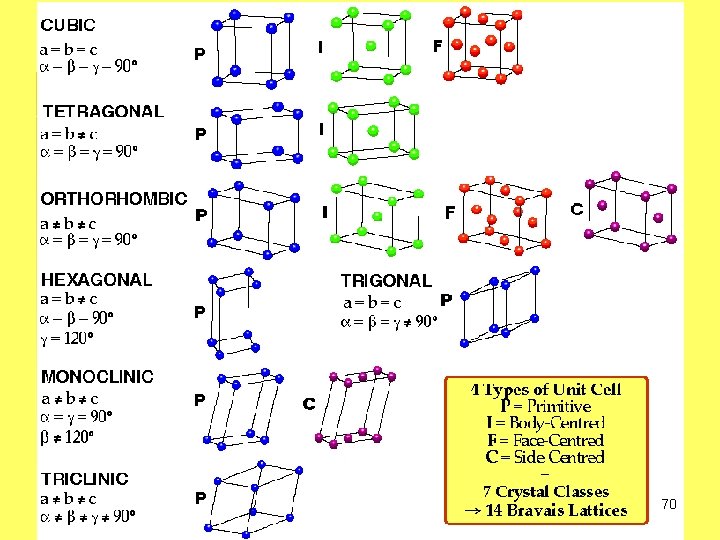
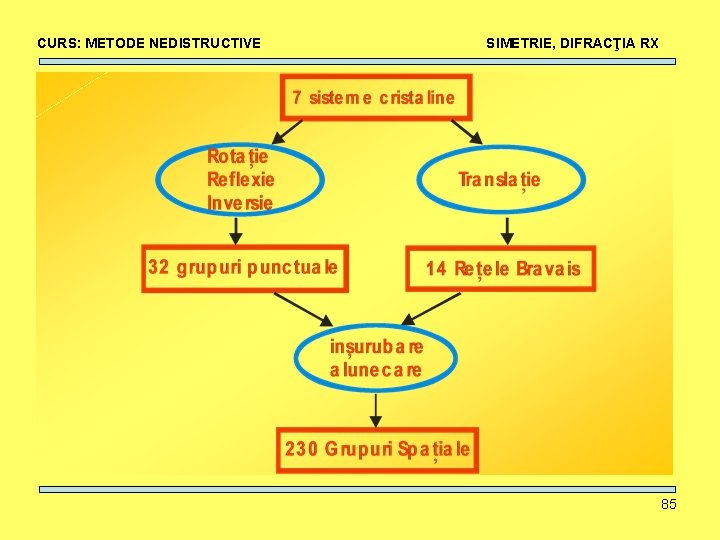
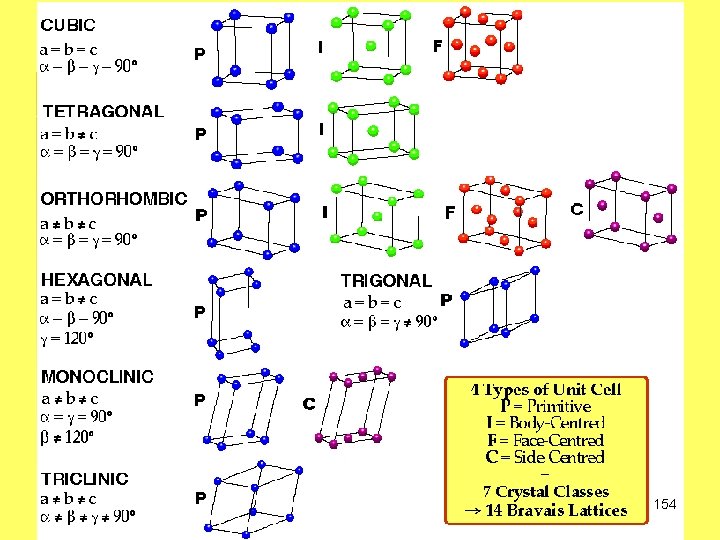
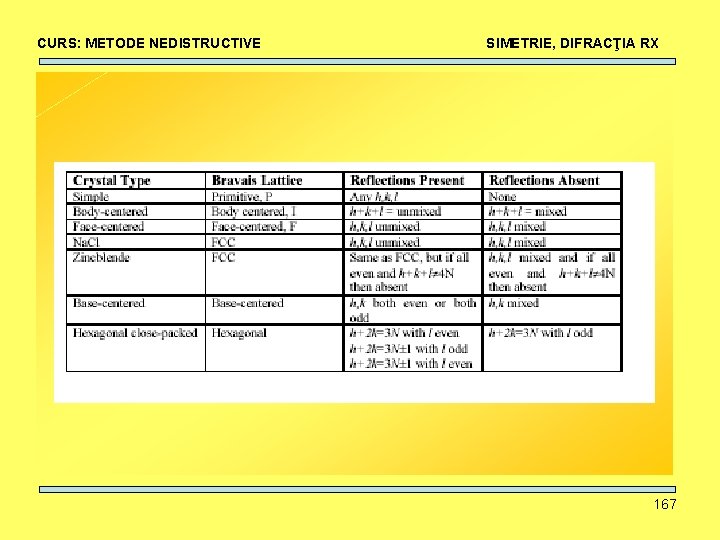
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţea Bravais: • reţea infinită de puncte discrete pentru care vecinătatea imediată este identică (trebuie să respecte proprietatea de translaţie). • setul de puncte obţinute cu ajutorul a trei vectori necoplanari a 1, a 2, a 3 cu R = n 1 a 1 + n 2 a 2 + n 3 a 3 (n 1, n 2, n 3 numere întregi). • Există 4 (+1 neprimitivă) reţele Bravais în 2 -D şi 7 (+7 neprimitive) în 3 -D. Ele pot fi diferenţiate prin diferitele operaţii de simetrie care le caracterizează. 41

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţele Bravais Neprimitive: • orice reţea se poate descrie cu o celulă elementară primitivă • prin centrare (feţe, baze, muchii, volum) se obţin celule neprimitive • Nodurile unei reţele trebuie să fie indiscernabile (adica fiecare nod are vecinatate identică = aceeasi privelişte). Prin centrare, trebuie ca şi pentru reţeaua nou formată această regulă să fie îndeplinită. 42

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţele Bravais Neprimitive: • Pentru fiecare sistem cristalin, reţeaua Bravais trebuie să aiba o simetrie minimă corespunzatoare. Prin centrare, reţeaua nou formată trebuie să respecte simetria minimă a reţelei primitive mamă. • Doar cea mai mica celulă, care cel mai mic număr de noduri care conservă simetria cerută poate fi considerată ca şi celulă a unei reţele Bravais. • De ce doar 14 reţele Bravais ? (seminar) 43

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX CUM REPREZENTĂM CRISTALELE? 44

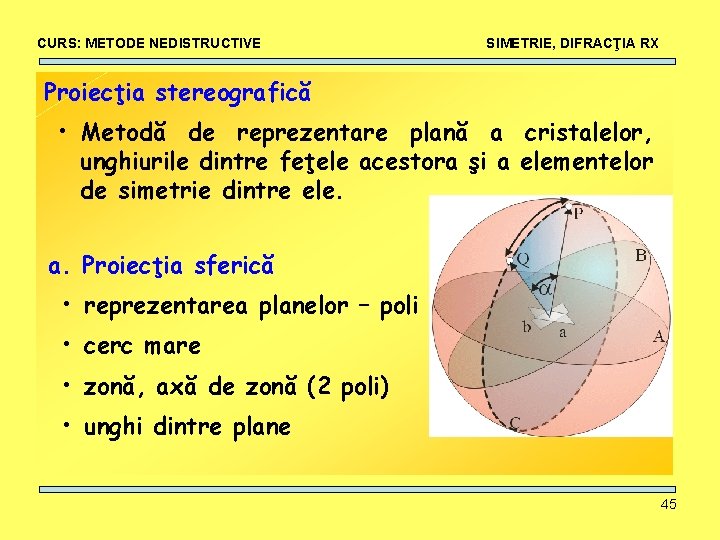
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Proiecţia stereografică • Metodă de reprezentare plană a cristalelor, unghiurile dintre feţele acestora şi a elementelor de simetrie dintre ele. a. Proiecţia sferică • reprezentarea planelor – poli • cerc mare • zonă, axă de zonă (2 poli) • unghi dintre plane 45

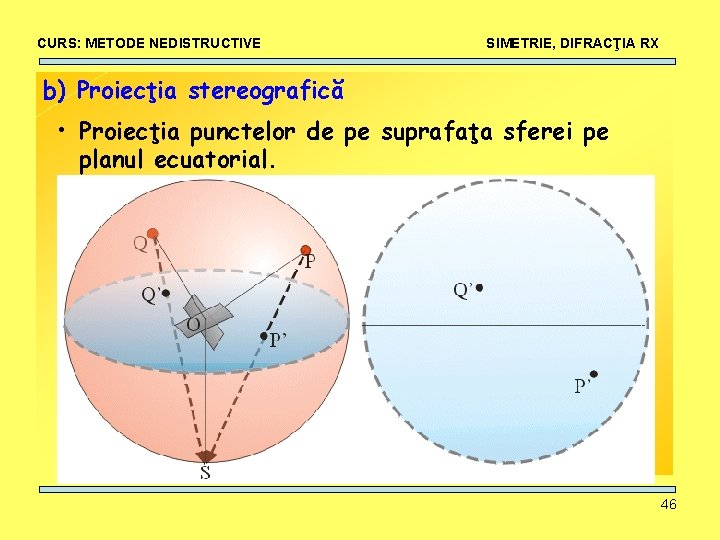
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX b) Proiecţia stereografică • Proiecţia punctelor de pe suprafaţa sferei pe planul ecuatorial. 46

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX b) Proiecţia stereografică • Proiecţia punctelor de pe suprafaţa sferei pe planul ecuatorial. • Unghiurile sunt păstrate însă distanţele sunt modificate. • Direcţiile cristaline apar în proiecţie ca şi puncte (poli) • Unghiurile se pot măsura folosind reţeaua Wulff. • Cercurile pe suprafaţa sferei rămân cercuri în proiecţia stereografică 47

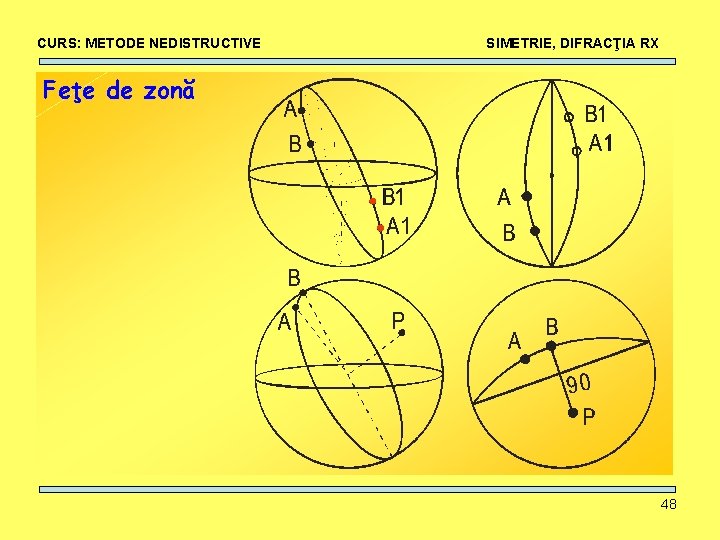
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Feţe de zonă 48

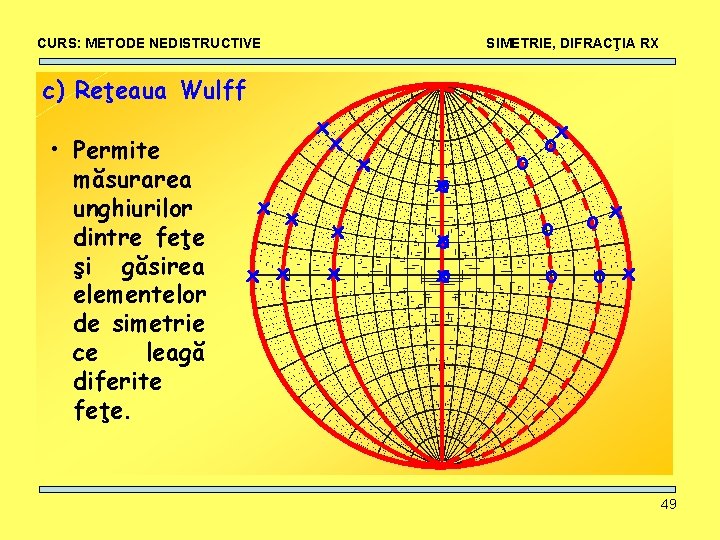
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX c) Reţeaua Wulff • Permite măsurarea unghiurilor dintre feţe şi găsirea elementelor de simetrie ce leagă diferite feţe. x x x x x o o x o o o x 49

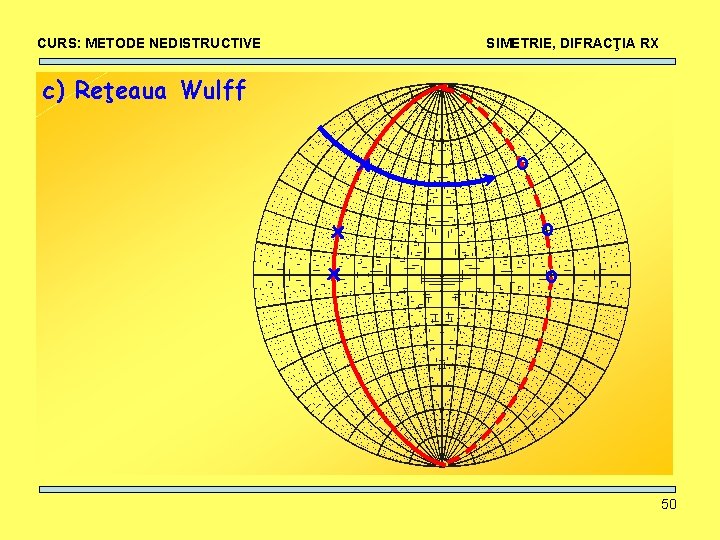
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX c) Reţeaua Wulff x o x o 50

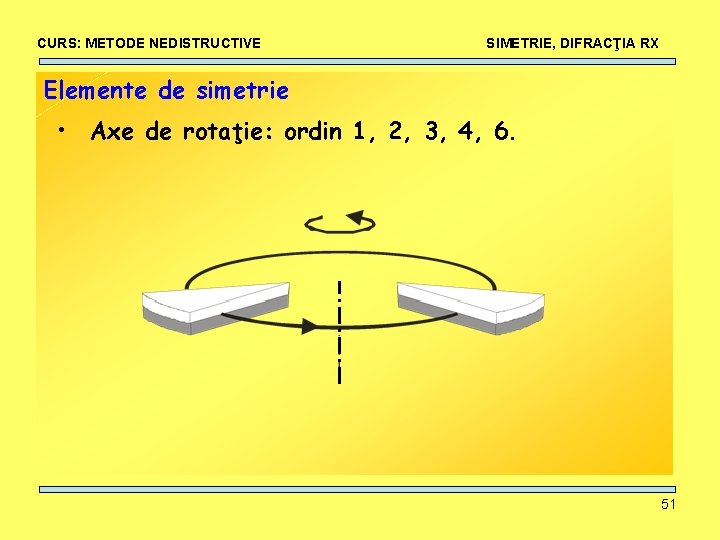
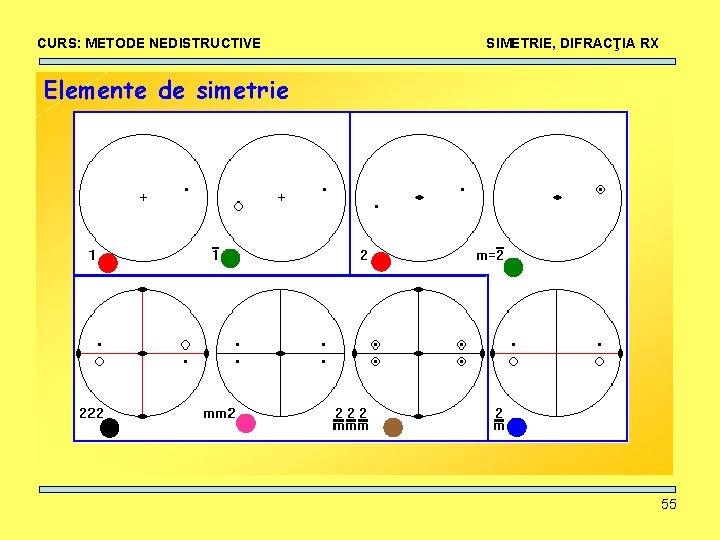
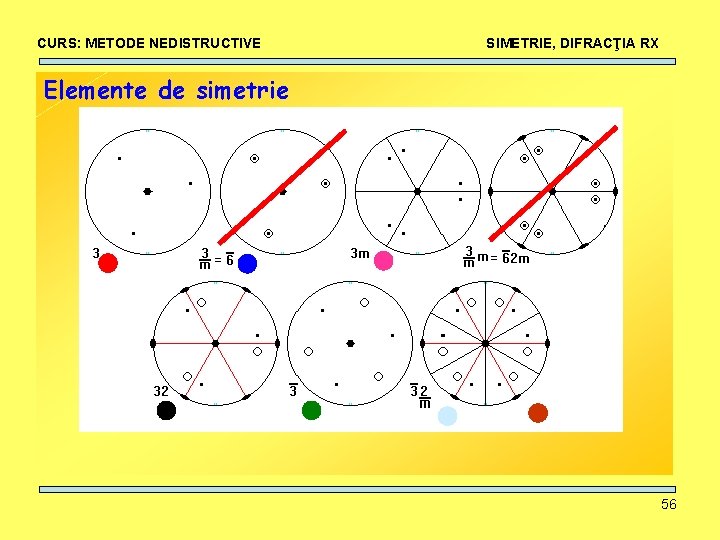
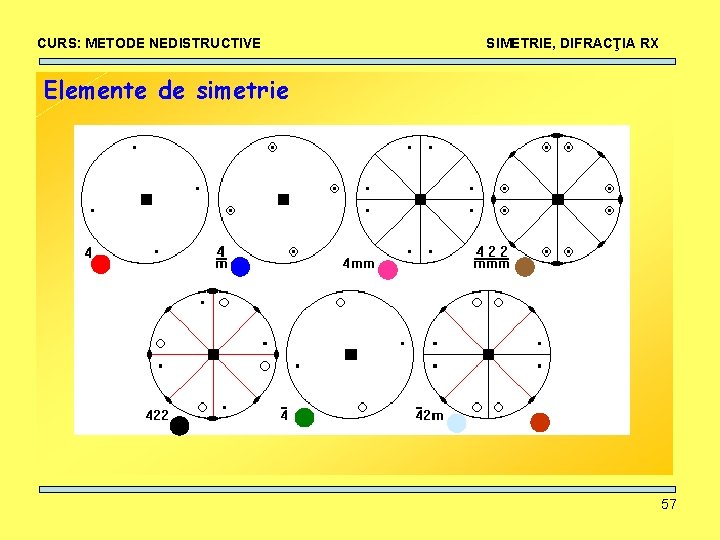
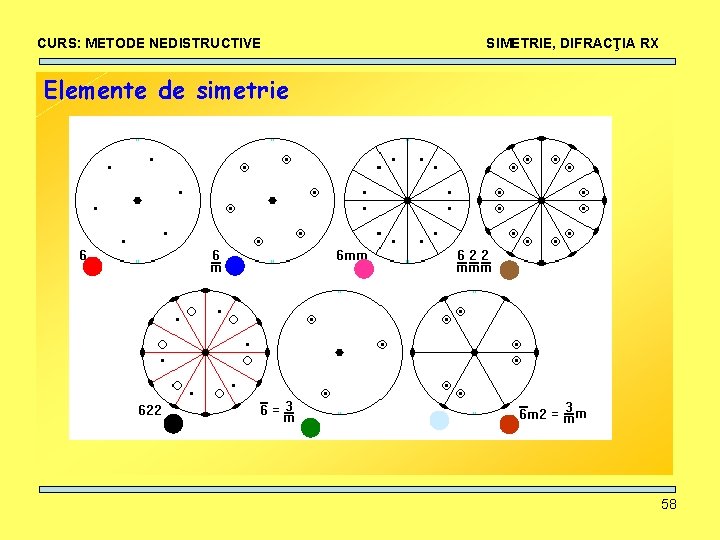
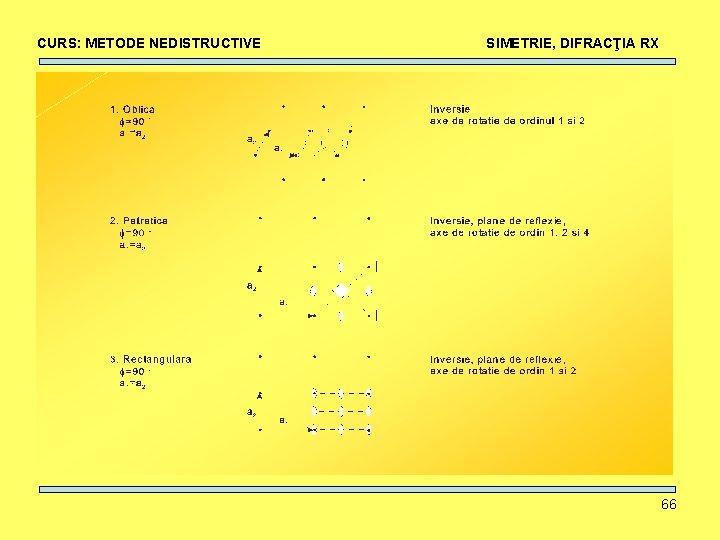
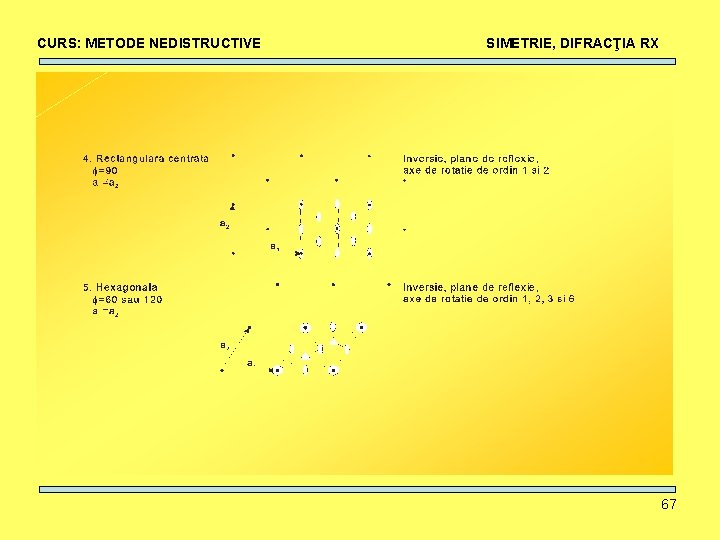
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie • Axe de rotaţie: ordin 1, 2, 3, 4, 6. 51

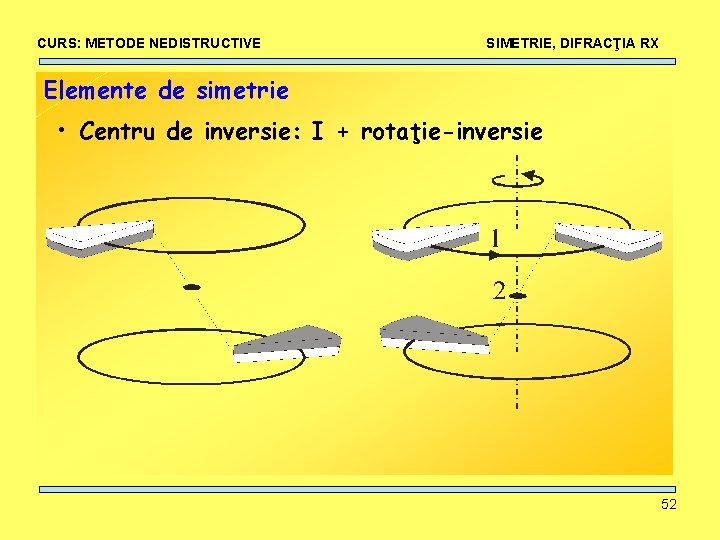
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie • Centru de inversie: I + rotaţie-inversie 52

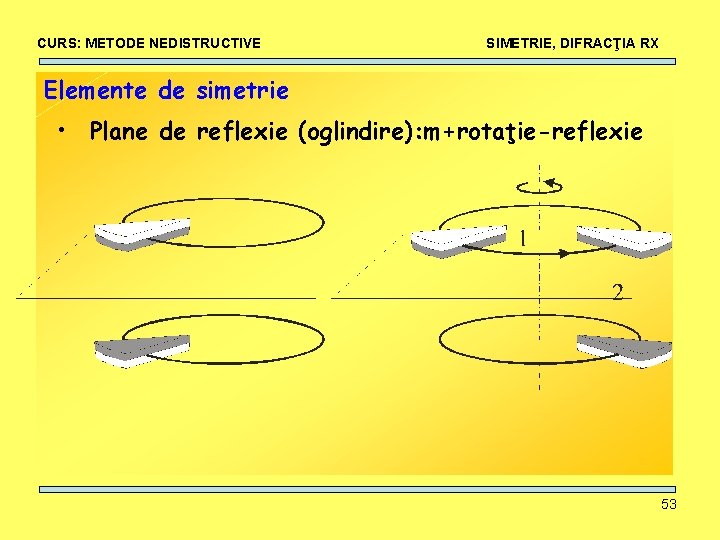
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie • Plane de reflexie (oglindire): m+rotaţie-reflexie 53

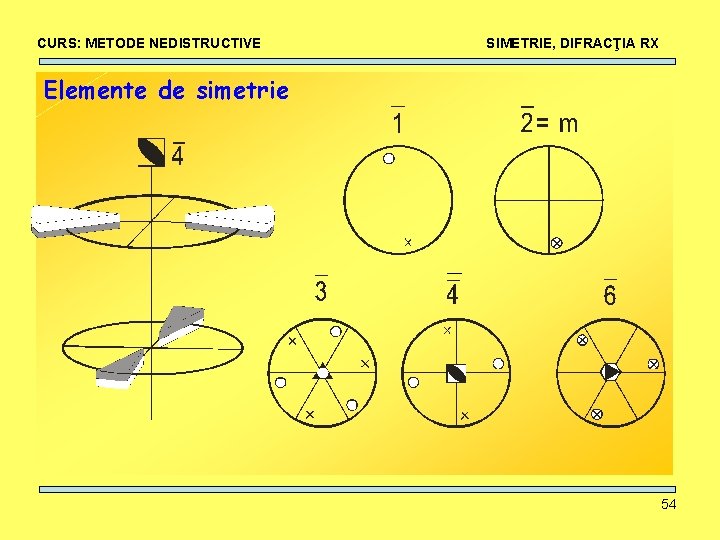
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 54

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 55

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 56

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 57

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 58

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Elemente de simetrie 59

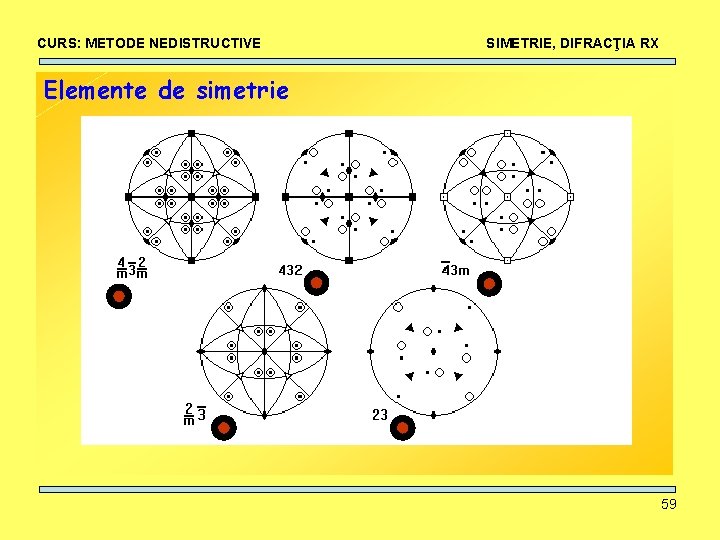
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Rotaţie, reflexie, inversie + combinaţii = 32 grupuri punctuale de simetrie 60

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Notaţia Herman-Mauguin pentru grupurile punctuale de simetrie: X : axă directă de ordinul X : 1, 2, 3, 4, 6 X : axă inversă de ordinul X : 1, 2=m, 3, 4, 6 X/m : axă directă de ordinul X şi plan de reflexie perpendicular pe X (2/m, 4/m, 6/m) 61

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Notaţia Herman-Mauguin pentru grupurile punctuale de simetrie: Xm || X : axă directă de ordinul X şi plan de reflexie mm 2, 3 m, 4 mm, 6 mm X 2 : axă directă de ordinul X şi axă de ordinul 2 perpendiculară pe X 222, 32, 422, 622 Xm X : axă inversă de ordin X şi plan de reflexie || 32/m, 42 m, 6 m 2 62

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Notaţia Herman-Mauguin pentru grupurile punctuale de simetrie: X 2 : axă inversă de ordin X şi axă de ordin 2 perpendiculară pe X 3 m, 4 m 2, 62 m X 3 : axă directă de ordinul X verticală şi axă de ordin 3 inclinată la 54 grade faţă de axa de ordin X X/mm: axă directă de ordin X, plan de reflexie paralel şi perpendicular 2/m 2/m, 4/m 2/m, 6/m 2/m sau (mmm, 4/mmm, 6/mmm) 63

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţele Bravais 2 D 64

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţele Bravais Neprimitive: • Condiţia de vecinătate identică • Pentru fiecare sistem cristalin, reţeaua Bravais trebuie să aiba o simetrie minimă corespunzatoare. Prin centrare, reţeaua nou formată trebuie să respecte simetria minimă a reţelei primitive mamă. • Doar cea mai mica celulă, care cel mai mic număr de noduri care conservă simetria cerută poate fi considerată ca şi celulă a unei reţele Bravais. 65

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 66

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 67

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţele Bravais 3 D 68

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX În 3 D există 7 posibilităţi diferite (din punct de vedere al elementelor noi de simetrie pe care le introduce fiecare optiune) de a alege vectorii de reţea şi unghiurile dintre ei 7 reţele Bravais primitive + 7 centrate = 14 reţele Bravais 3 D. 69

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 70

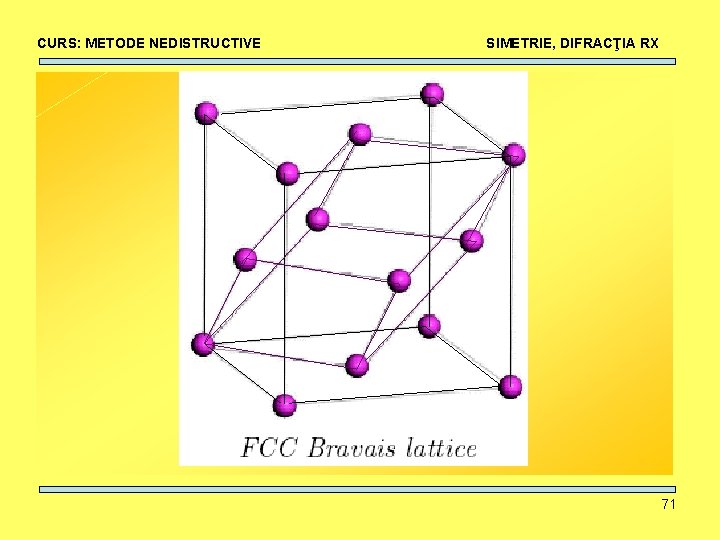
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 71

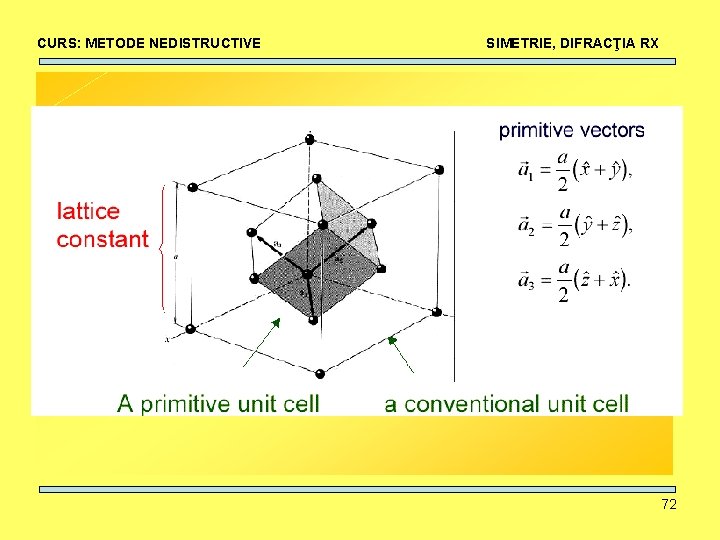
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 72

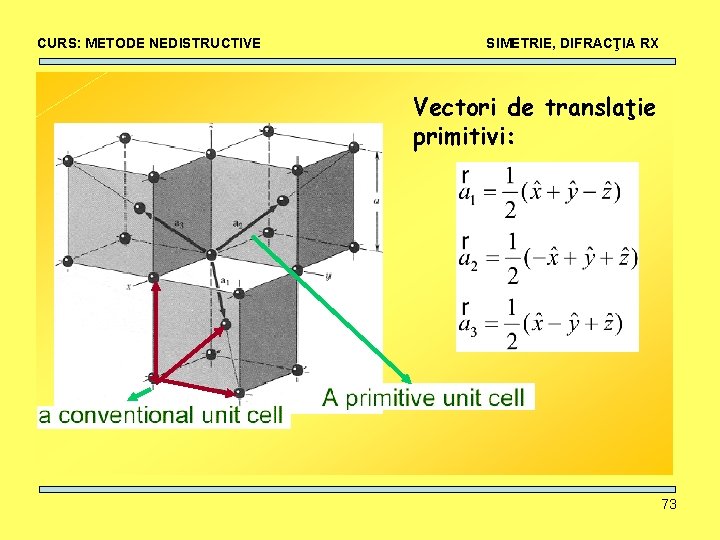
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Vectori de translaţie primitivi: 73

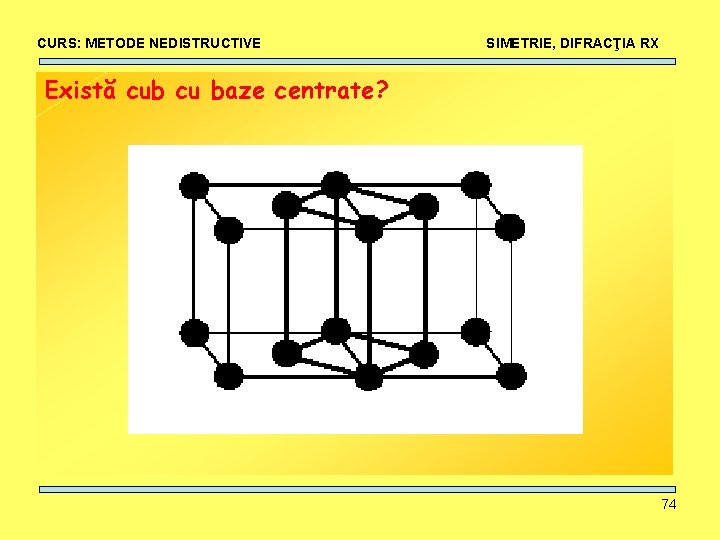
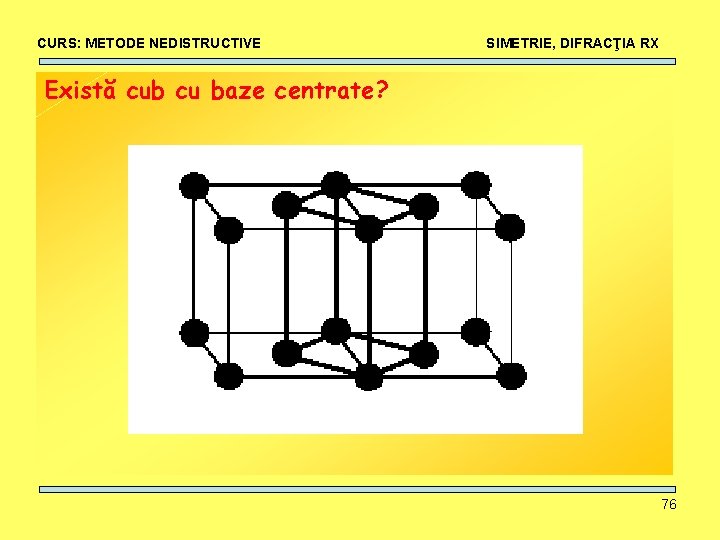
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Există cub cu baze centrate? 74

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Există cub cu baze centrate? Reţele Bravais Neprimitive: • Condiţia de vecinătate identică • Pentru fiecare sistem cristalin, reţeaua Bravais trebuie să aiba o simetrie minimă corespunzatoare. Prin centrare, reţeaua nou formată trebuie să respecte simetria minimă a reţelei primitive mamă. • Doar cea mai mica celulă, care cel mai mic număr de noduri care conservă simetria cerută poate fi considerată ca şi celulă a unei reţele Bravais. 75

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Există cub cu baze centrate? 76

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 77

CURS: METODE NEDISTRUCTIVE Semnificaţia ordinii simbolurilor simetrie din grupurile punctuale: SIMETRIE, DIFRACŢIA RX elementelor de 78

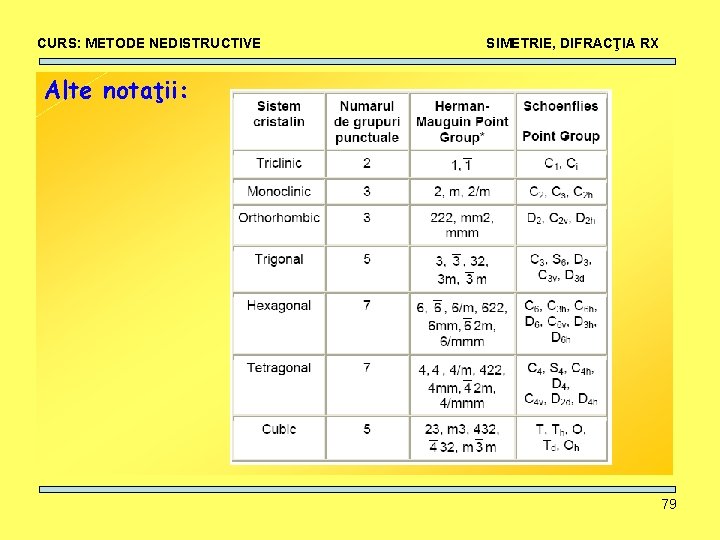
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Alte notaţii: 79

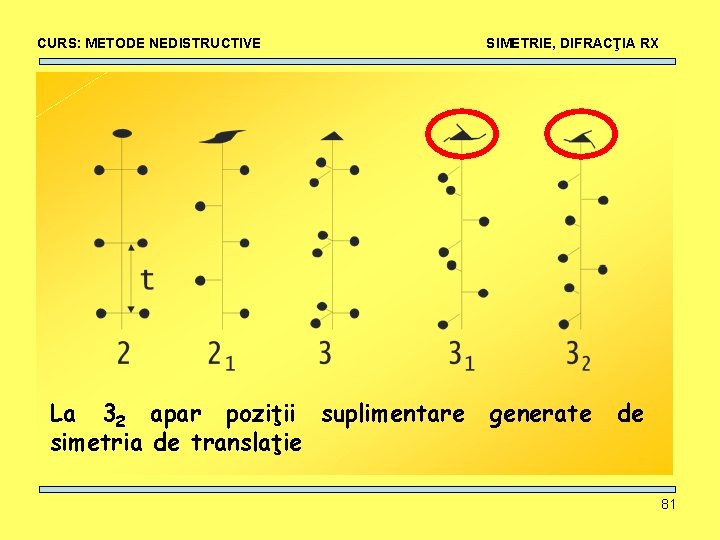
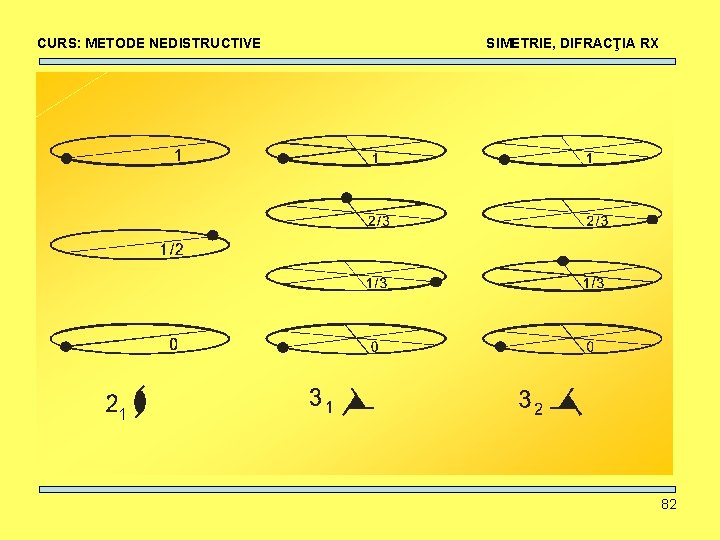
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Dacă adăugăm şi combinaţia elementelor de simetrie cu translaţia: 230 grupuri spaţiale de simetrie: Axe elicoidale: rotaţie + translaţie || axa nm= rotaţie in sens trigonometric în jurul unei axe de ordin n urmată de o translaţie fracţionară cu m/n (m n) din perioada t paralelă cu axa de rotaţie. 80

CURS: METODE NEDISTRUCTIVE La 32 apar poziţii suplimentare simetria de translaţie SIMETRIE, DIFRACŢIA RX generate de 81

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 1 82

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Plane de reflexie cu alunecare = reflexie în raport cu un plan urmată de o translaţie cu o fracţiune din vectorul de translaţie din acel plan. . În exemplul de mai sus, translaţia a fost făcută cu 83

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Nomenclatura pentru plane de reflexie cu alunecare: 84

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 85

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemple: CVC W: Gr. Sp. : Im 3 m; Gr. P. : m 3 m CFC Al: Gr. Sp. : Fm 3 m; Gr. P. : m 3 m CFC Si: Gr. Sp. : Fd 3 m; Gr. P. : m 3 m d = reflexie + aluncare cu 1/4 de-a lungul diagonalei <111> Mg Hexagonal: Gr. Sp. : P 63/mmc; Gr. P. : 6/mmm c = reflexie + alunecare cu 1/2 de-a lungul axei c 63 = axă de înşurubare de ordin 3 86

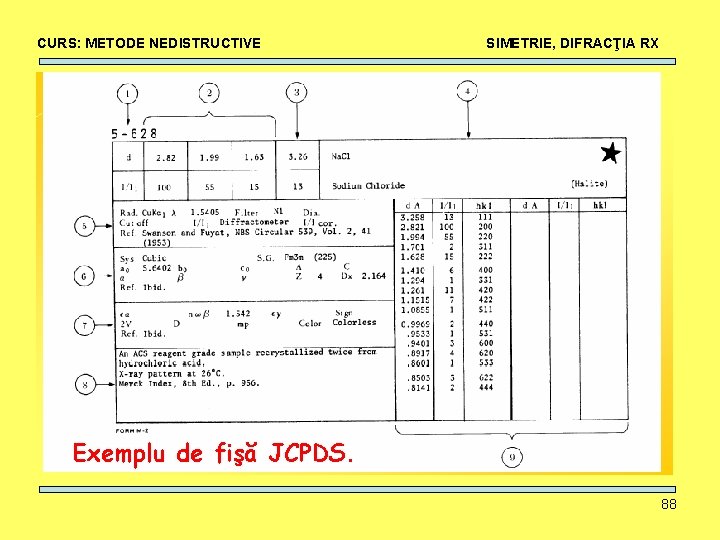
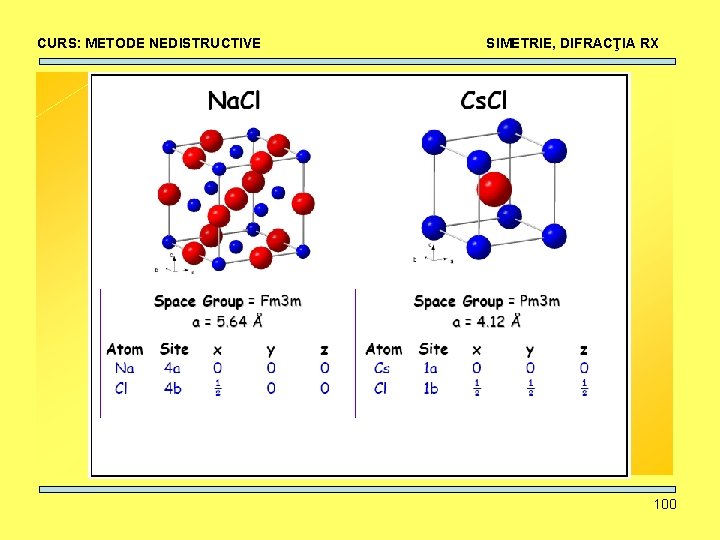
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Prima literă din grupul spaţial (SISTEMUL INTERNAŢIONAL sau HERMANN – MAGUIN) indică: I = celulă elementară centrată în volum, F = celulă elementară centrată pe feţe, P = celulă primitivă, A, B, C = faţa A sau B sau C a celulei elementare este centrată. Acest sistem este metoda preferată pentru descrierea structurilor cristaline pentru metale si ceramice. Folosit de JCPDS (Joint Committee on Powder Diffraction Standards, ICDD acum) în bazele de date cristalografice. 87

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemplu de fişă JCPDS. 88

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 1: numărul fişierului 2: cele mai intense trei linii 3: linia de la cel mai mic unghi 4: formula chimică şi numele substanţei 5: informaţii despre metoda de difracţie folosită 6: date cristalografice 7: proprietăţi optice şi altele 8: date despre probă 9: difracţie: intensităţile sunt relative (faţă de linia cea mai intensă). Semnul din dreapta sus: calitatea datelor: stea = calitate bună, i = linii indexate dar valorile intensităţilor nu sunt de încredere, c = calculat, o = criteriu de încredere scăzut (low reliability). 89

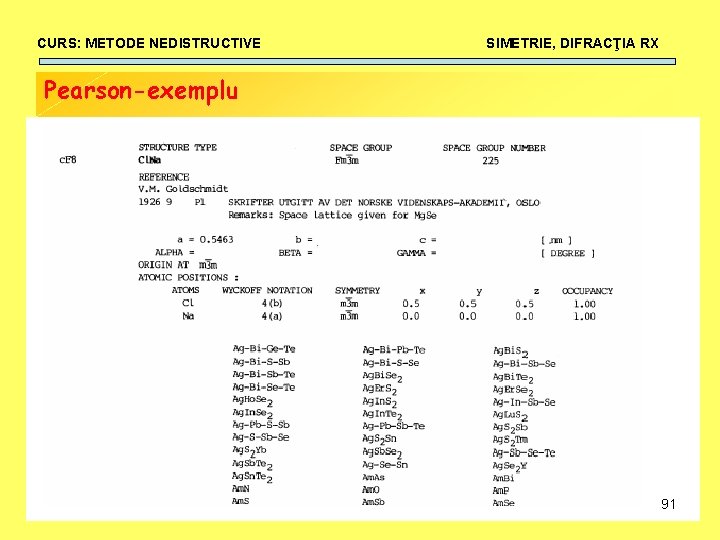
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX După PEARSON: Prima literă: a=triclinic (anorthic), m=monoclinic, o=ortorombic, t=tetragonal, h=hexagonal sau romboedral, c=cubic A doua literă: A, B sau C = faţa A sau B sau C este centrată. F=feţe centrate, I=volum centrat, P=primitivă Număr indicând numărul de atomi pe celula elementară 90

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Pearson-exemplu 91

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Poziţii echivalente corespunzatoare diverselor reţele Bravais structura cristalină = reţea + bază. Bază: fiecărui nod din reţea îi asociem un atom sau un grup de atomi. trebuie să dam coordonatele bazei faţă de un singur nod iar coordonatele celolalţi atomi, asociaţi celorlalte noduri se pot genera uşor ştiind că nodurile sunt echivalente şi că de la o celulă la alta ajungem cu ajutorul vectorului de translaţie 92

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Poziţii echivalente corespunzatoare diverselor reţele Bravais TOATE NODURILE DIN REŢEA SUNT ECHIVALENTE DACĂ AVEM REŢELE NEPRIMITIVE, CELULA ELEMENTARĂ CONŢINE MAI MULTE NODURI, DAR TOATE SUNT ECHIVALENTE. 93

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 94

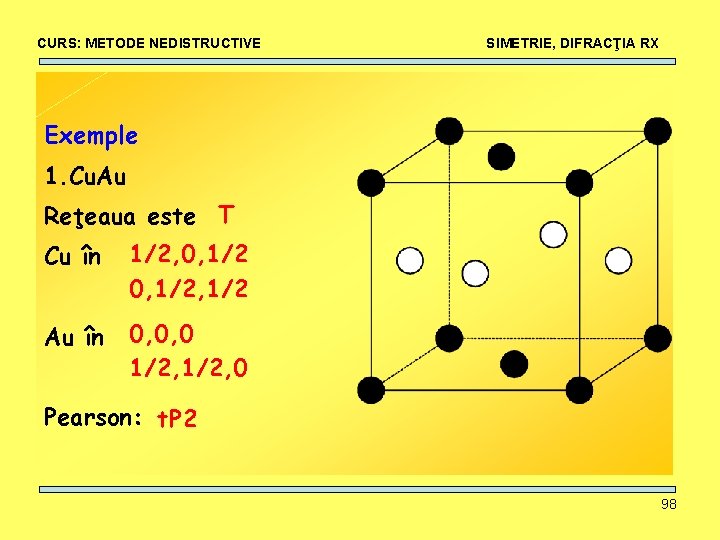
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Descrierea structurilor Pentru descrierea unei structuri cristaline, în general, trebuie precizat: 1. sistemul cristalin, grupul spaţial 2. parametrii de reţea 3. parametrii atomici (x, y, z) ai bazei. x, y si z sunt fracţii din parametri de reţea a, b şi c. , 4. numărul (Z) de formule chimice unitate pe celula elementară 5. densitatea calculată comparată cu valoarea masurată, 95

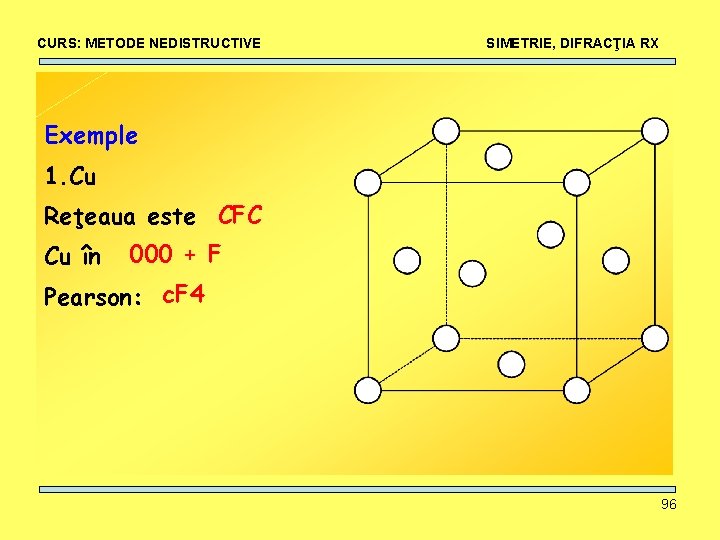
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemple 1. Cu Reţeaua este CFC Cu în 000 + F Pearson: c. F 4 96

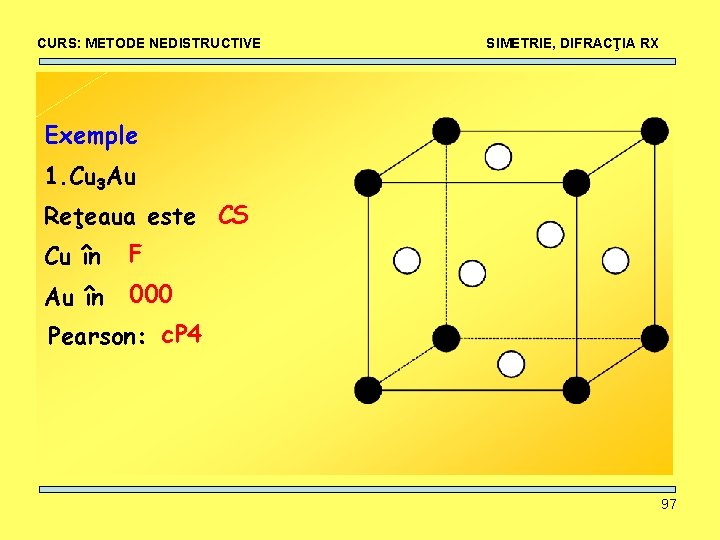
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemple 1. Cu 3 Au Reţeaua este CS Cu în F Au în 000 Pearson: c. P 4 97

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemple 1. Cu. Au Reţeaua este T Cu în 1/2, 0, 1/2, 1/2 Au în 0, 0, 0 1/2, 0 Pearson: t. P 2 98

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX ITC 99

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 100

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 101

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 102

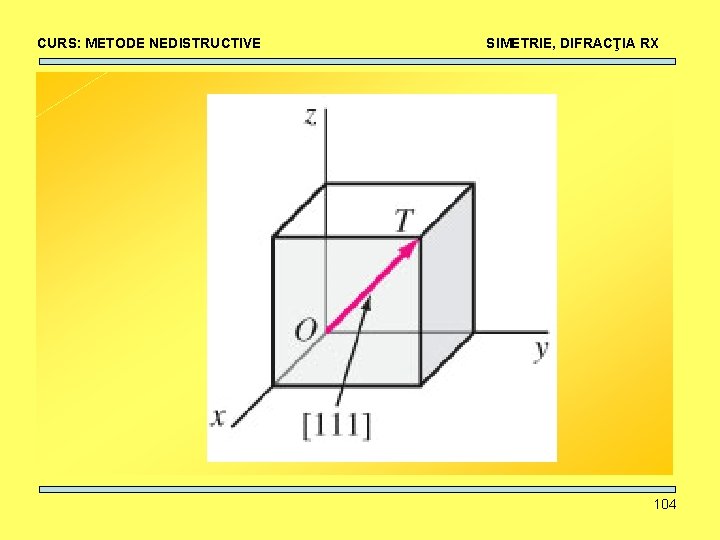
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Direcţii reticulare. Se notează cu [uvw], unde u, v şi w sunt cele mai mici numere, prime între ele, ce descriu coordonatele (în unităţi a, b sau c) ale primului nod intersectat de paralela la acea dreaptă care trece prin origine 103

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 104

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 210 X=1, Y=½, Z=0 [1 ½ 0] [2 1 0] X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2] 105

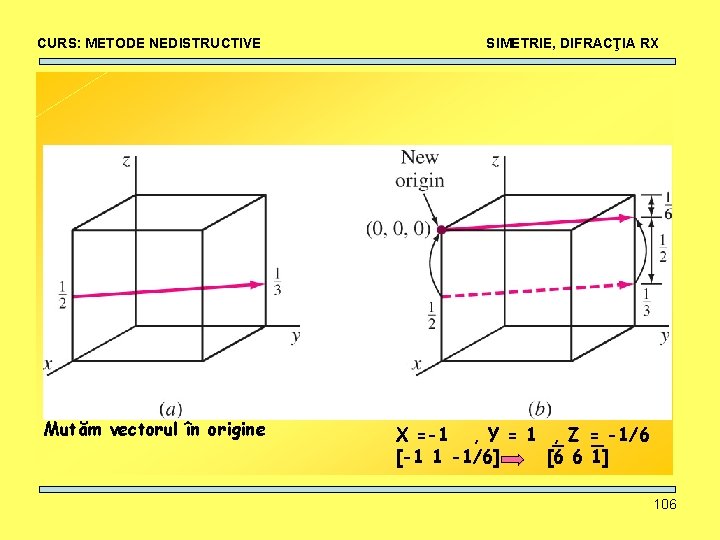
CURS: METODE NEDISTRUCTIVE Mutăm vectorul în origine SIMETRIE, DIFRACŢIA RX X =-1 , Y = 1 , Z = -1/6 [-1 1 -1/6] [6 6 1] 106

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Plane cristaline • Set de plane paralele ce trec prin nodurile reţelei. • Densitatea de noduri este aceeaşi în fiecare plan al unui set de plane. • Toate nodurile reţelei sunt cuprinse în fiecare set de plane. Familii de plane în reţele 2 D b b a a 107

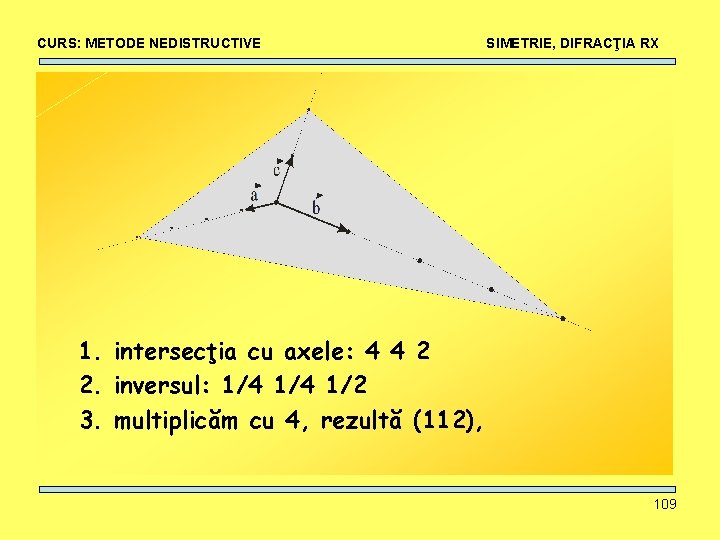
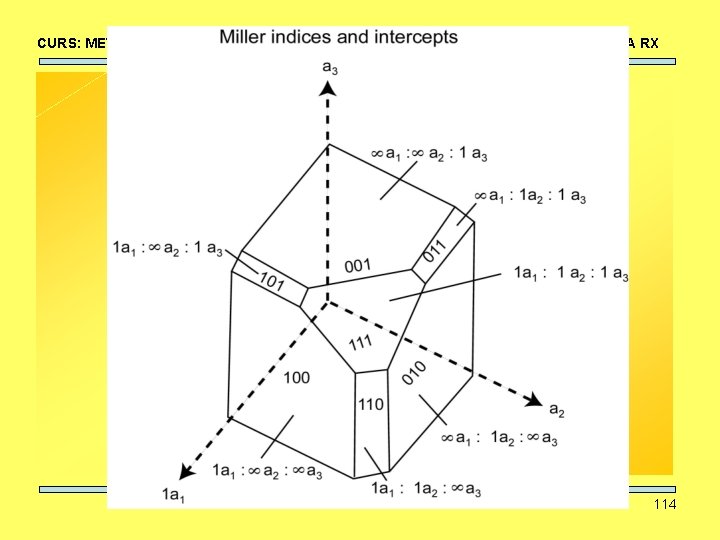
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Indicii Miller • Reprezentare simbolică a planelor cristaline • Definiţi ca inversul coordonatelor punctelor de intersecţie ale planului cu axele cristalografice. • Deci pentru a determina indicii Miller ai unui plan trebuie să: 1. Determinăm coordonatele punctelor de intersecţie ale planului cu cele trei axe cristalografice 2. Calculăm inversul acestor trei coordonate 3. Dacă obţinem numere fracţionare, amplificăm toate valorile a. î. Să obţinem numere întregi. 108

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 1. intersecţia cu axele: 4 4 2 2. inversul: 1/4 1/2 3. multiplicăm cu 4, rezultă (112), 109

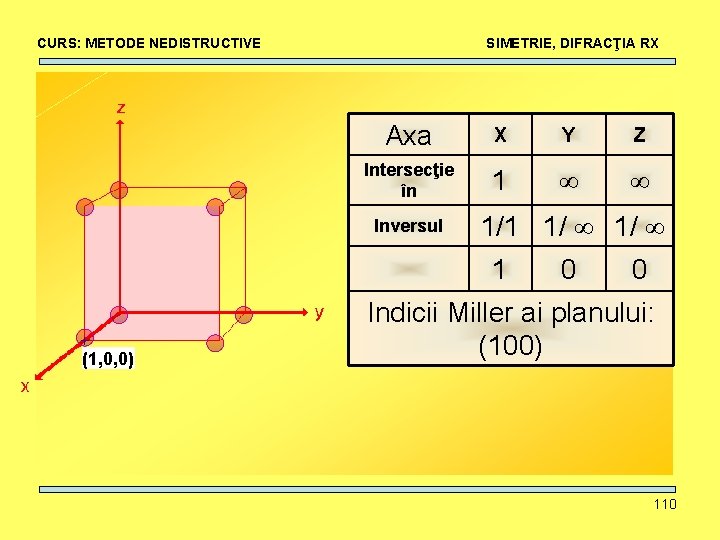
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Axa X Y Z Intersecţie în 1 ∞ ∞ Inversul 1/1 1/ ∞ 1 (1, 0, 0) 0 0 Indicii Miller ai planului: (100) 110

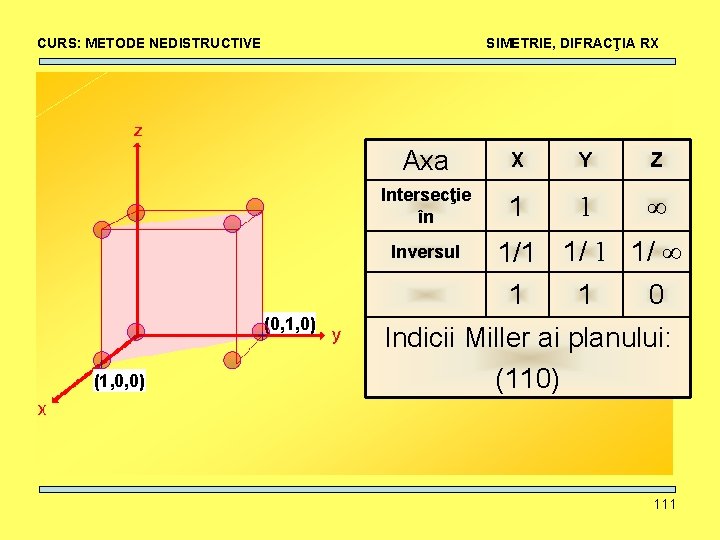
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Axa X Y Z Intersecţie în 1 1 ∞ Inversul 1/1 1/ ∞ 1 (0, 1, 0) (1, 0, 0) 1 0 Indicii Miller ai planului: (110) 111

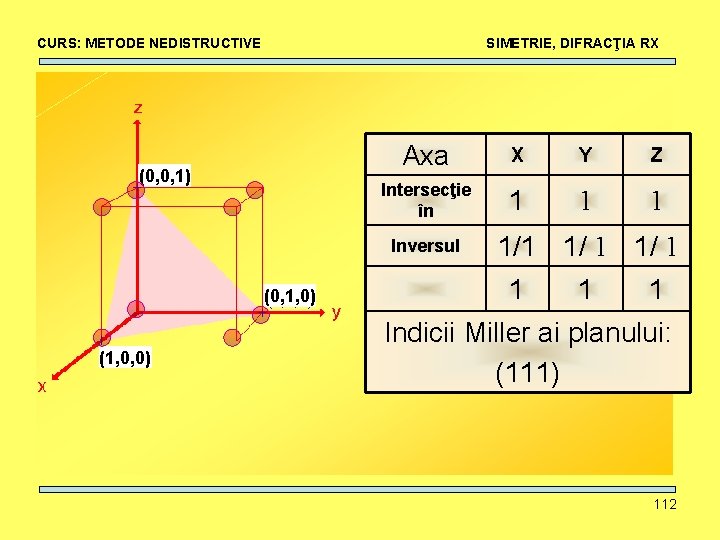
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX (0, 0, 1) Axa X Y Z Intersecţie în 1 1 1 Inversul (0, 1, 0) (1, 0, 0) 1/1 1/ 1 1 Indicii Miller ai planului: (111) 112

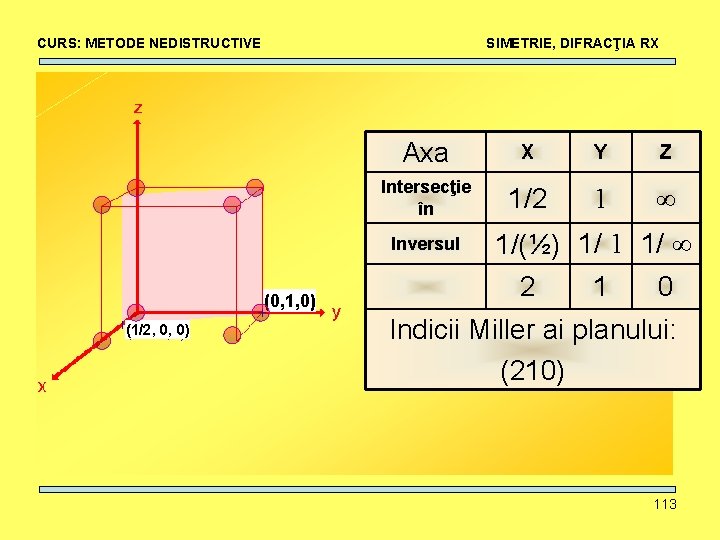
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Axa X Y Z Intersecţie în 1/2 1 ∞ Inversul (0, 1, 0) (1/2, 0, 0) 1/(½) 1/ 1 1/ ∞ 2 1 0 Indicii Miller ai planului: (210) 113

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 114

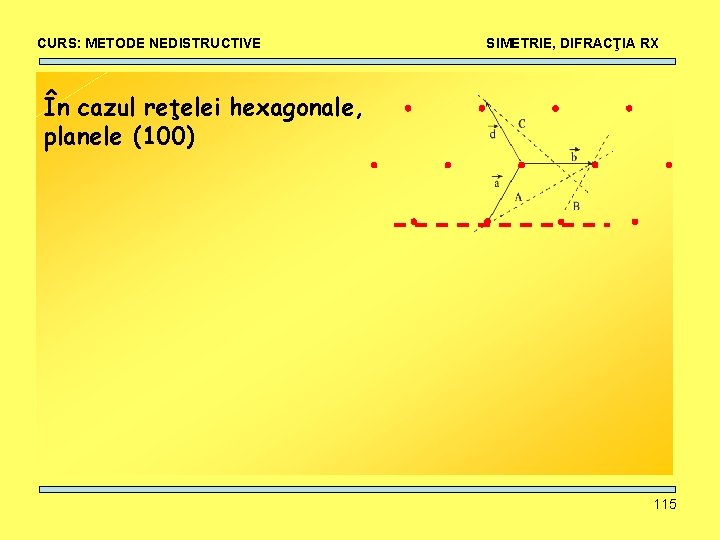
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX În cazul reţelei hexagonale, planele (100) 115

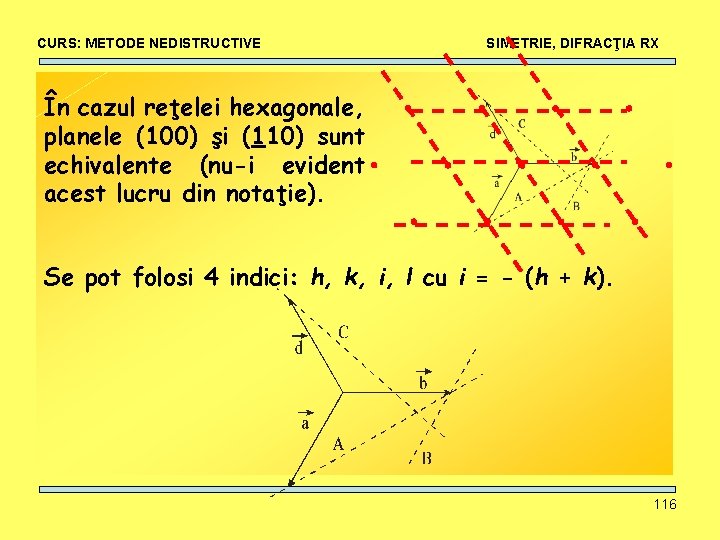
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX În cazul reţelei hexagonale, planele (100) şi (110) sunt echivalente (nu-i evident acest lucru din notaţie). Se pot folosi 4 indici: h, k, i, l cu i = - (h + k). 116

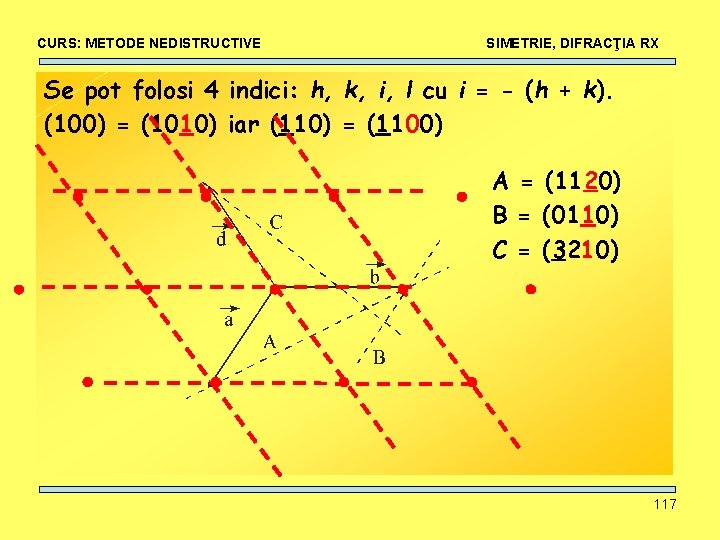
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Se pot folosi 4 indici: h, k, i, l cu i = - (h + k). (100) = (1010) iar (110) = (1100) A = (1120) B = (0110) C = (3210) 117

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Ştiind tipul structurii si parametri de reţea, se poate calcula distanţa interplanară dhkl. 118

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX REŢEAUA RECIPROCĂ Dacă a, b si c sunt vectorii care definesc reţeaua reală, vectorii reţelei reciproce sunt definiţi prin: unde V este volumul celulei elementare din spaţiul direct. 119

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX • Pornind de la A, B, C, la fel ca şi în reţeaua directă, se poate construi prin translaţia acestora o reţea = reţea reciprocă şi se pot defini celule elementare, reţele Bravais în spaţiul invers, etc. . • Definim în reţeaua reciprocă un vector de translaţie la fel ca şi în reţeaua directă, combinaţie de vectori de bază de forma: unde hkl sunt numere întregi. 120

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 1. Vectorul este perpendicular pe planul (hkl) al reţelei. 2. Mărimea lui este de 2 ori mare decât inversul distanţei dintre planele (hkl). 121

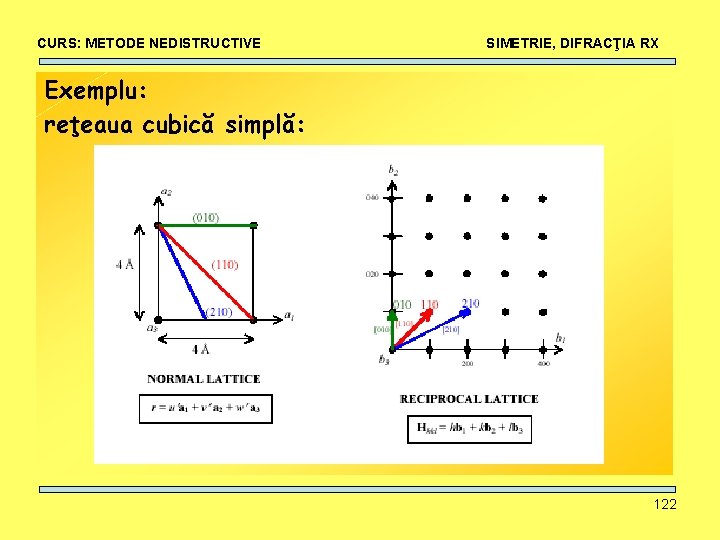
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemplu: reţeaua cubică simplă: 122

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 123

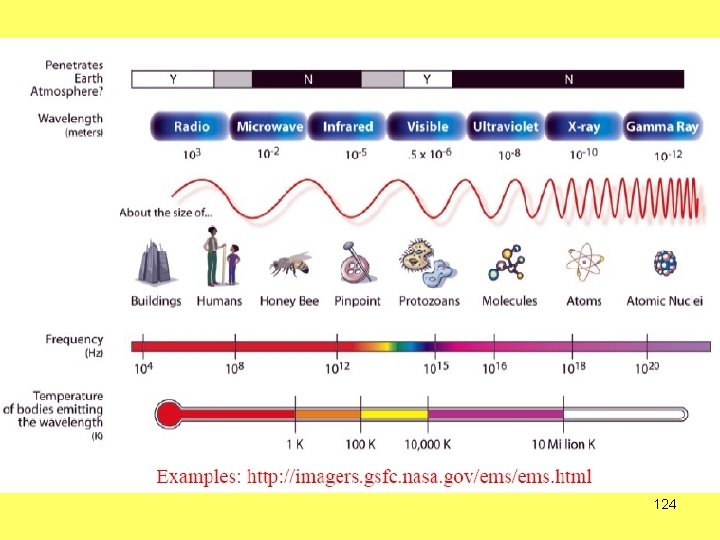
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 124

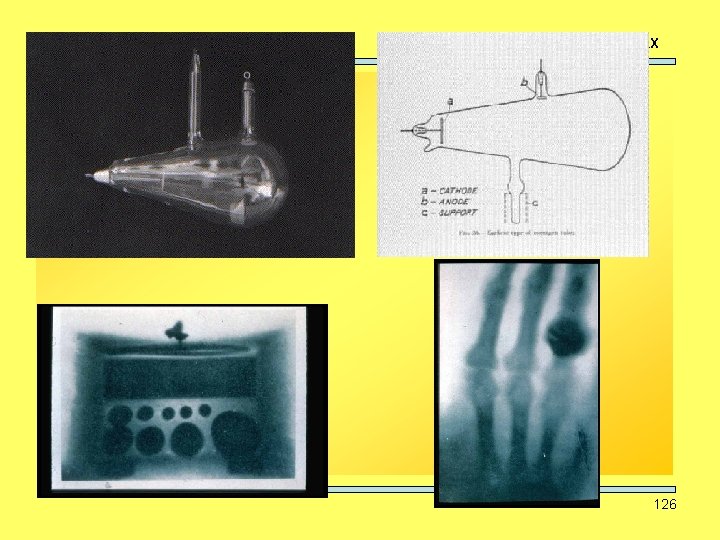
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Descoperirea razelor X November 1895, Würzburg Wilhelm Conrad Röntgen 125

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 126

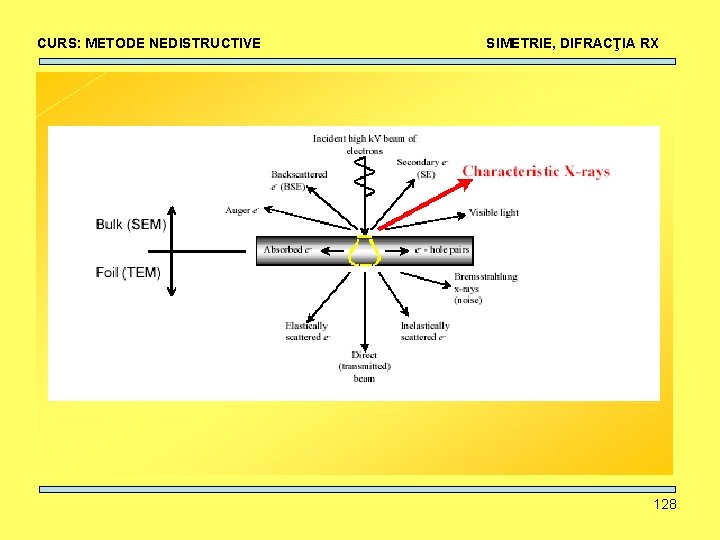
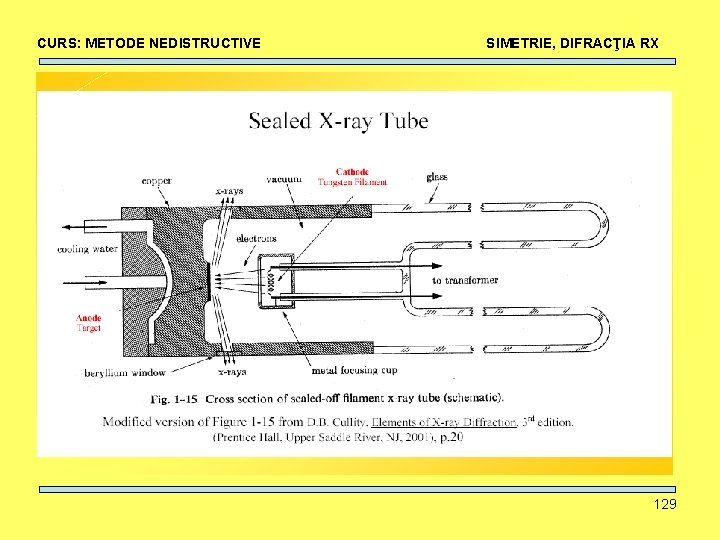
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Producerea Razelor X • filamentul catodului se încălzeşte prin effect Joule prin aplicarea unui current (amperi) ⇒ emisie de electroni. • electronii sunt acceleraţi înspre anod • electronii sunt focalizaţi printr-o combinaţie de câmpuri electrice. • când electronii se ciocnesc de ţintă (anod), ei pierd energie. Mai mult de 99% din energia lor se transformă în căldură mai puţin de 1% este convertită în Raze X. 127

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 128

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 129

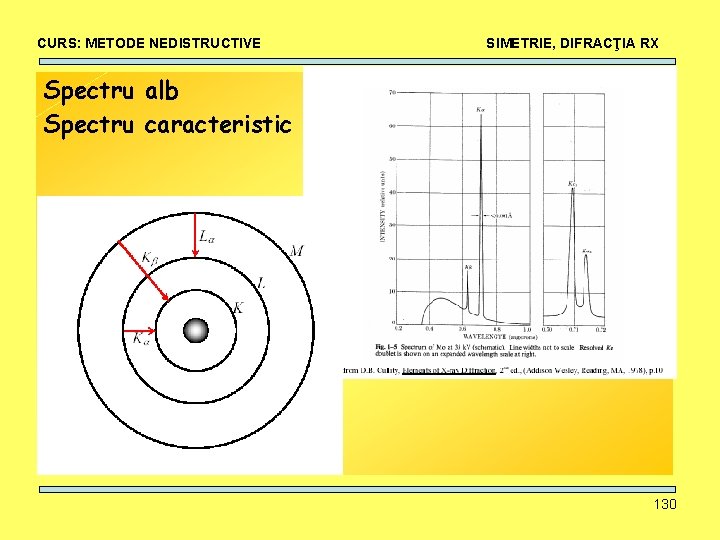
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Spectru alb Spectru caracteristic 130

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 131

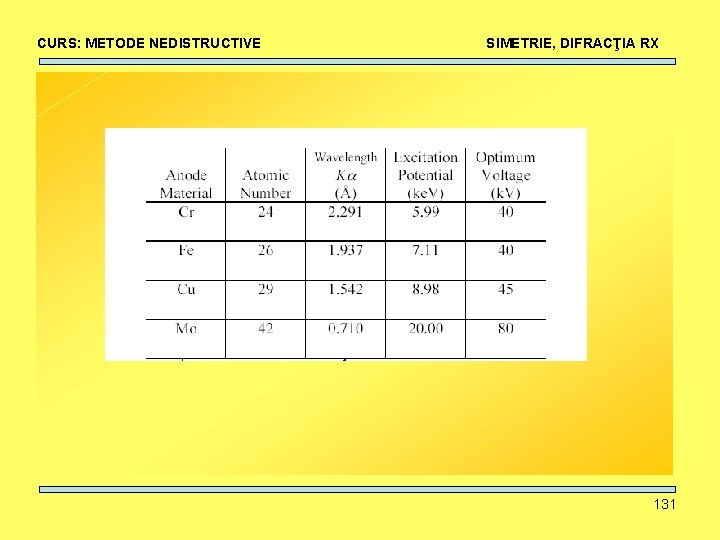
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Alegerea tipului de radiaţie folosită depinde de • Materialul de investigat • Fluorescenţă • Absorbţie • etc. Fluorescenţa • Apare când radiaţia incidentă scoate electroni de pe pătura K a atomului radiaţie adiţională Absorbţia • Dacă un element din probă are numărul atomic mai mic decât cel al anodului 132

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Exemplu: • Anod/Radiaţie: Cu/Cu. K (Z = 29), energie 8. 04 ke. V • Probă: Fe (Z = 26), energia de ionizare pentru electronii păturii K 7 ke. V Radiaţiile Cu. K au energie suficientă pentru extragerea unui electron de pe pătura K a fierului. emisie de radiaţie de fluorescenţă Soluţie: Folosirea Cr. K , E = 5. 41 ke. V. 133

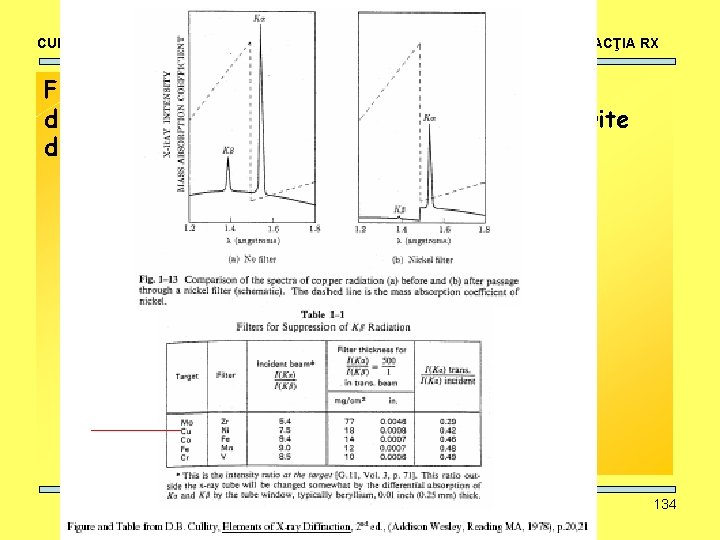
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Folosind-se caracteristicile de absorbţie a diferitelor materiale se pot elimina liniile nedorite din spectrul RX: FILTRE. 134

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Folosind-se caracteristicile de absorbţie a diferitelor materiale se pot elimina liniile nedorite din spectrul RX: FILTRE. Liniile K sunt cele mai folosite pentru că au energia cea mai mare şi sunt mai puţin absorbite de materialul investigat. 135

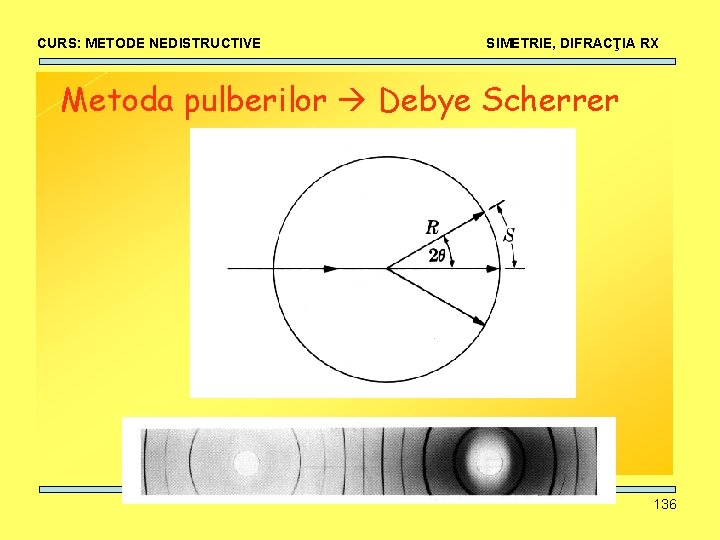
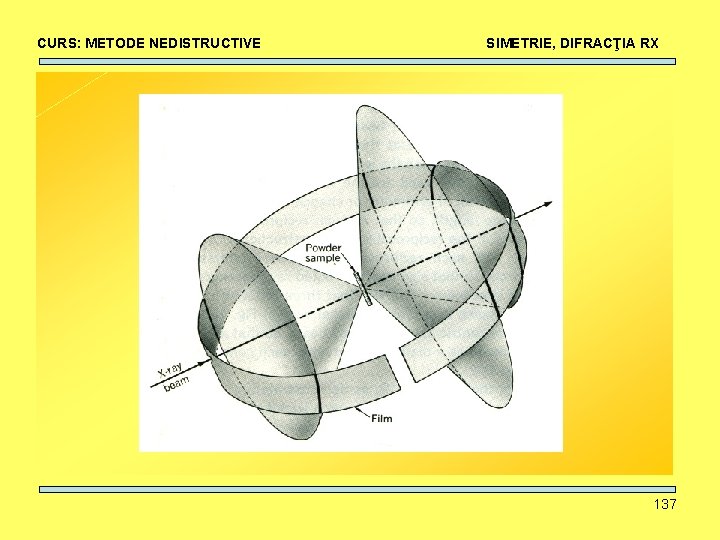
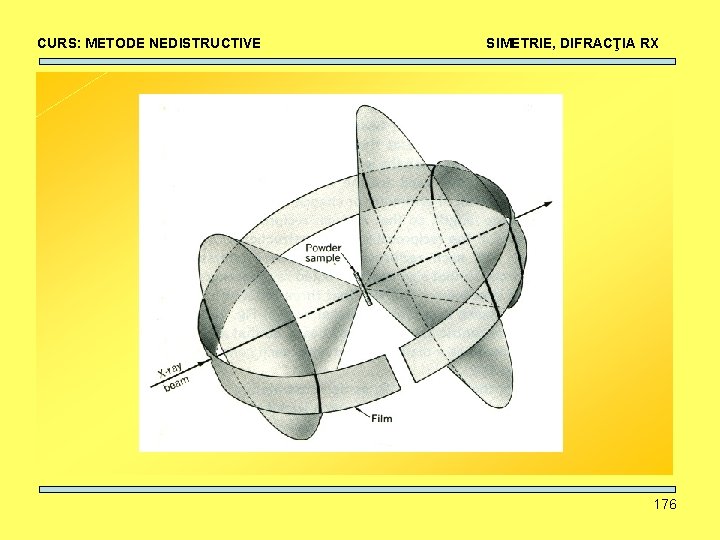
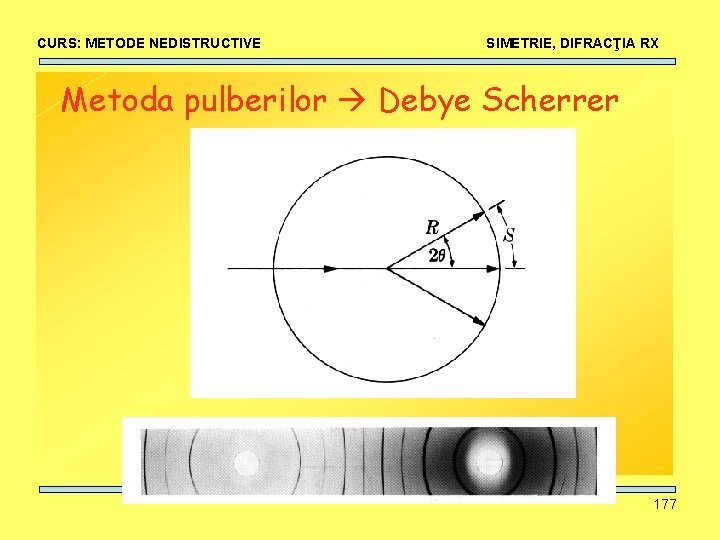
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Metoda pulberilor Debye Scherrer 136

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 137

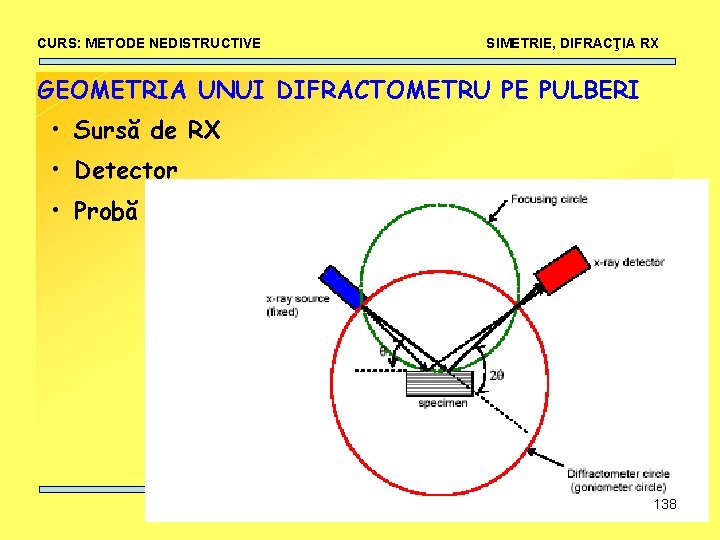
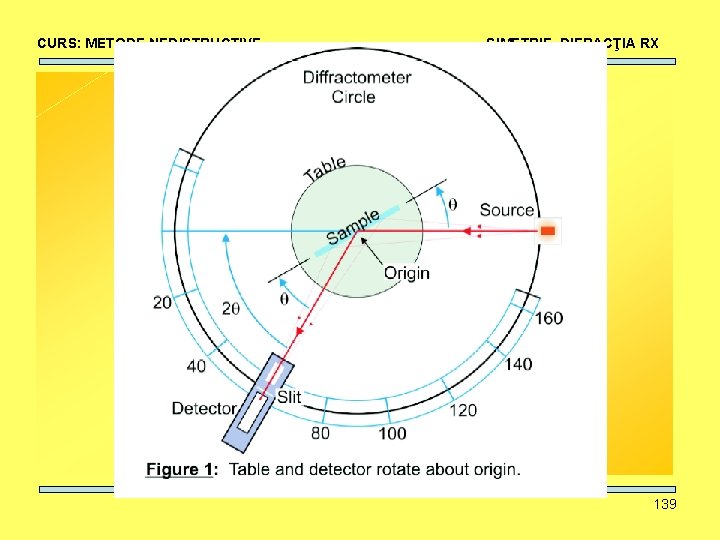
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX GEOMETRIA UNUI DIFRACTOMETRU PE PULBERI • Sursă de RX • Detector • Probă 138

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 139

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Proba: • pudră (mojarată) • plată (altfel peak-urile la unghiuri mici vor fi absorbite) • tensiunile duc la lărgirea peak-ulrilor şi la deplasarea lor • monocristal 140

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectori • Proporţionali • Cu scintilaţie • Cu corp solid 141

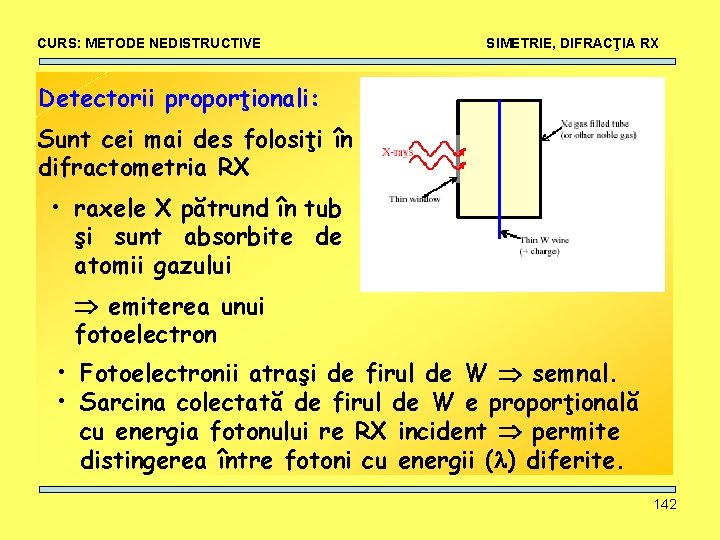
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectorii proporţionali: Sunt cei mai des folosiţi în difractometria RX • raxele X pătrund în tub şi sunt absorbite de atomii gazului emiterea unui fotoelectron • Fotoelectronii atraşi de firul de W semnal. • Sarcina colectată de firul de W e proporţională cu energia fotonului re RX incident permite distingerea între fotoni cu energii ( ) diferite. 142

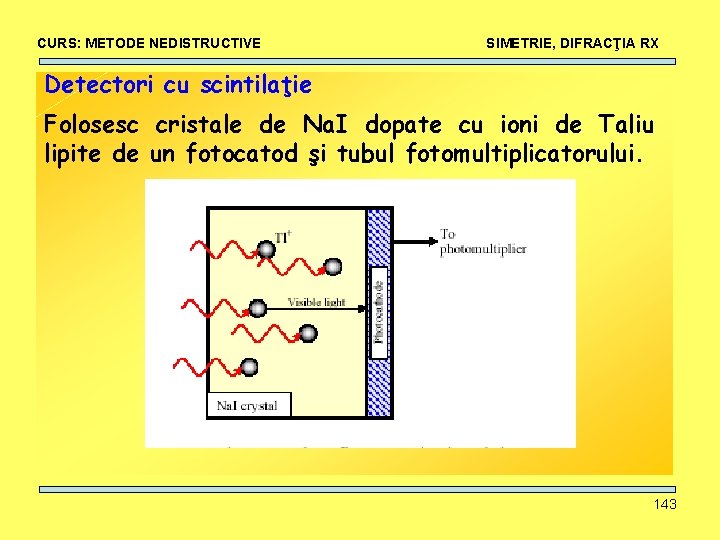
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectori cu scintilaţie Folosesc cristale de Na. I dopate cu ioni de Taliu lipite de un fotocatod şi tubul fotomultiplicatorului. 143

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectori cu scintilaţie Folosesc cristale de Na. I dopate cu ioni de Taliu lipite de un fotocatod şi tubul fotomultiplicatorului. • razele X incidente produc fluorescenţa cristalului • scintilaţie pentru fiecare foton RX absorbit • lumina este măsurată cu un fotomultiplicator • cantitatea de lumină emisă este proporţională cu intensitatea RX • Detectorii cu scintilaţie au rezoluţie mai mică decât cei proporţionali 144

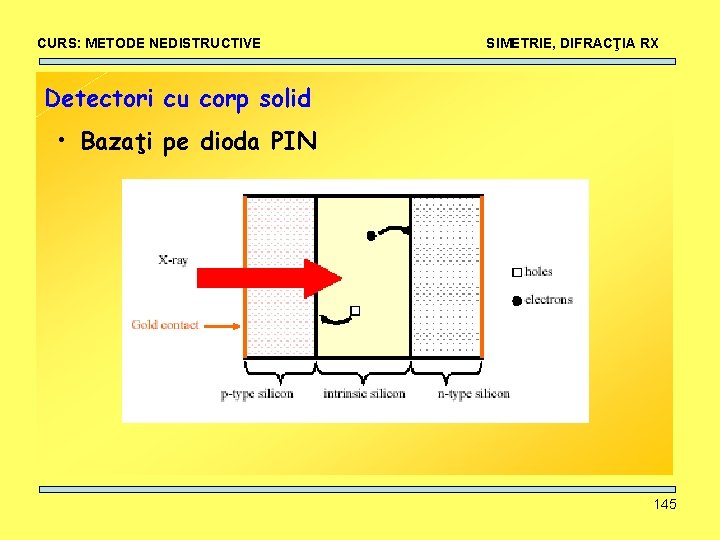
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectori cu corp solid • Bazaţi pe dioda PIN 145

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Detectori cu corp solid • Bazaţi pe dioda PIN • RX excită electroni din banda de valenţă în cea de conducţie pereche electron-gol • potenţialul aplicat jncţiunii separă electronii de goluri puls de sarcină care este măsurat • numărul de electroni sau goluri este direct proporţional cu energia fotonului RX • detectorii cu corp solid au cea mai bună eficienţă si rezoluţie 146

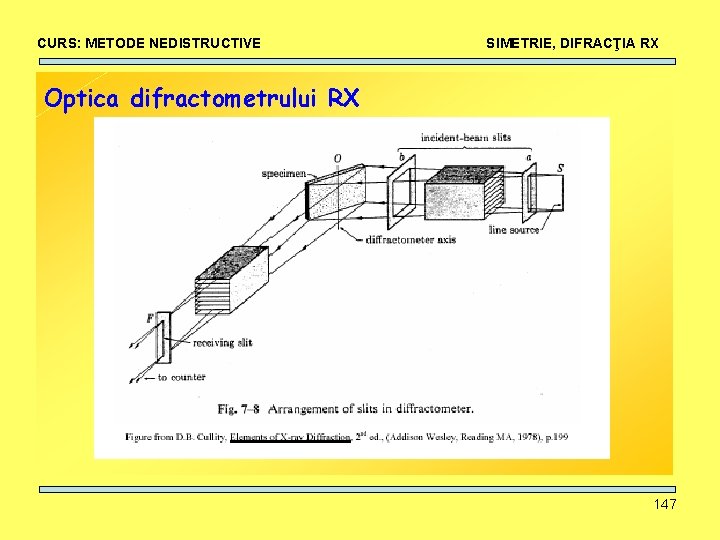
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Optica difractometrului RX 147

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Înregistrarea unei difractograme • mod continuu informaţii calitative • pas cu pas informaţii cantitative • Viteza de scanare, mărimea pasului şi durata de măsură/pas influenţează raportul semnal/zgomot: posibilitatea de a identifica peakuri de intensitate mică. Viteze de scanare tipice: 1 -2 grade (2 )/min sau pasul 0. 02 grade (2 secunde/pas) 148

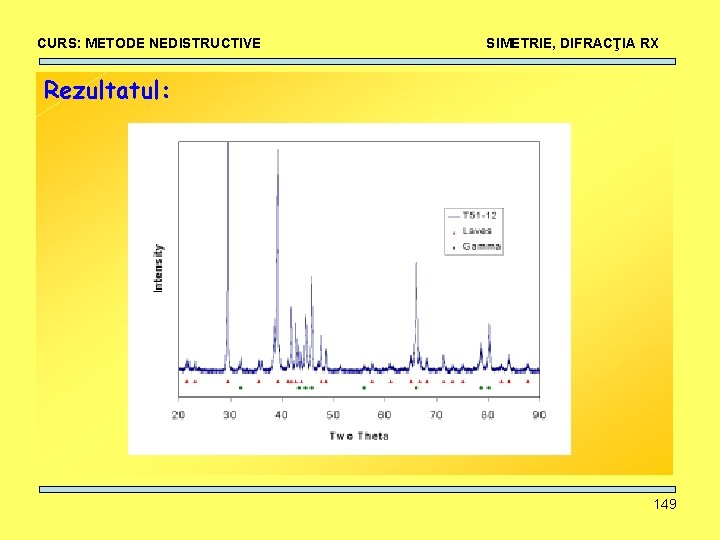
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Rezultatul: 149

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX ! FIECARE EXPERIMENT ESTE DIFERIT ! Poziţia peak-urilor depinde de: • lungimea de undă folosită • structura cristalină • dimensiunea cristalitelor Ex. Ti (CVC) 150

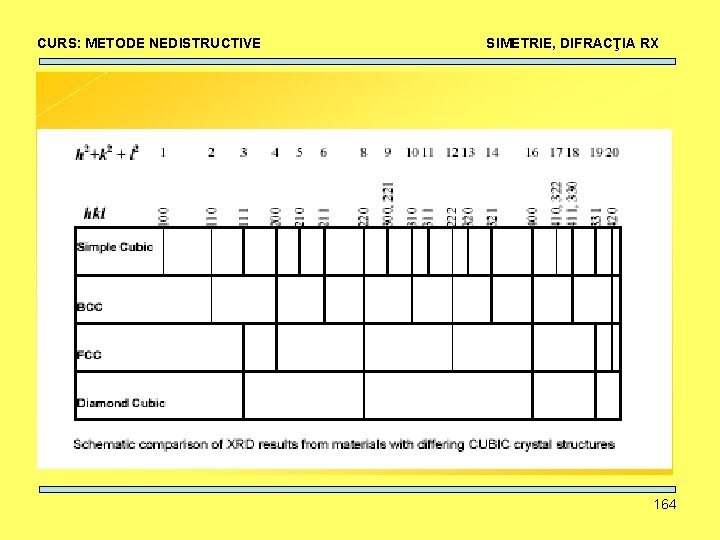
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Structura cristalină: • O structură cristalină de simetrie joasă are mai multe peakuri decât una de simetrie înaltă. • Cristalele de simetrie cubică – simetrie înaltă – au un mic număr de reflexii. • Pentru structurile de simetrie cubică este posibilă determinarea tipului de reţea (CVC, CFC, CS) considerând periodicitatea reflexiilor observate. 151

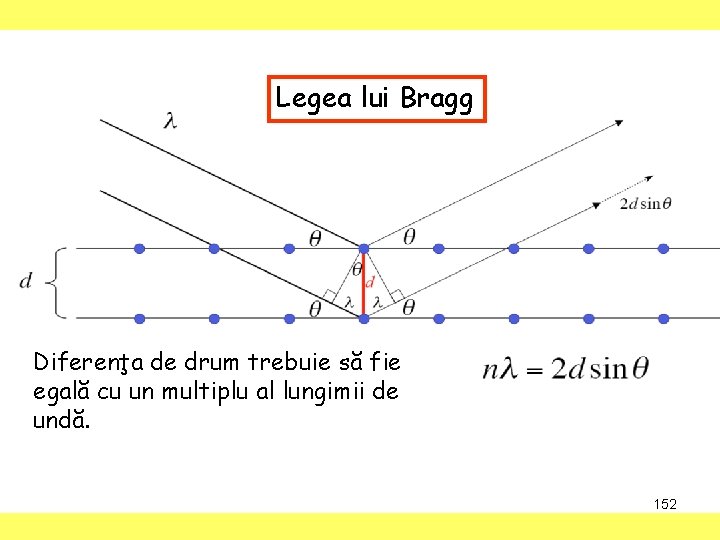
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Legea lui Bragg Diferenţa de drum trebuie să fie egală cu un multiplu al lungimii de undă. 152

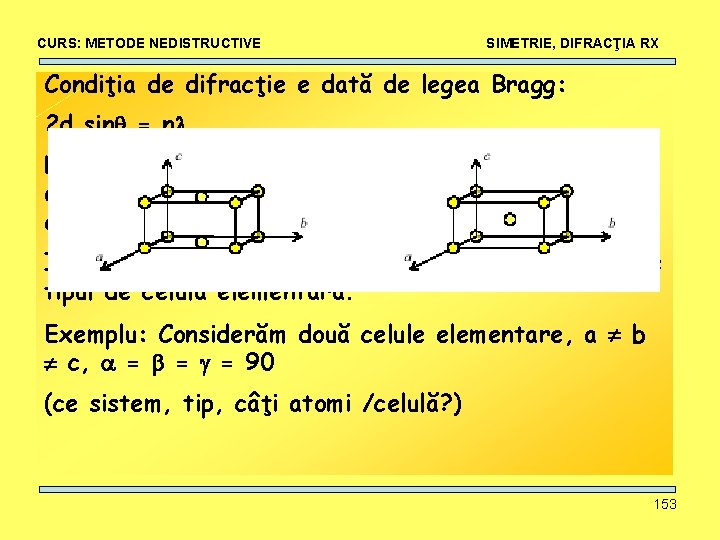
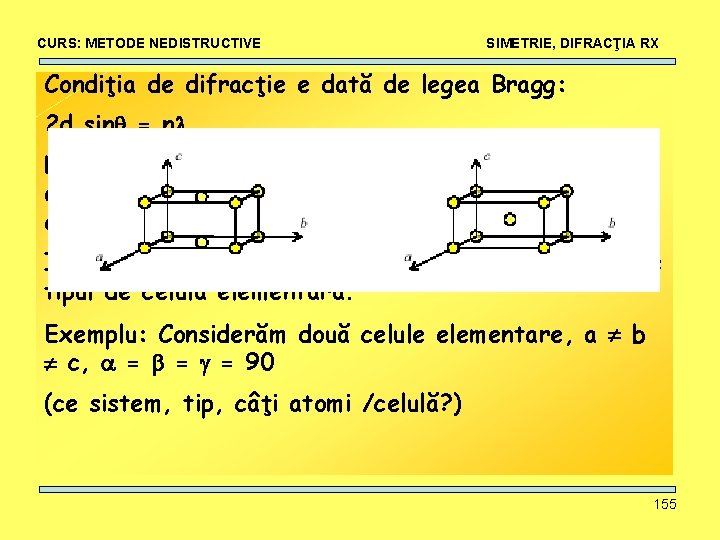
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Condiţia de difracţie e dată de legea Bragg: 2 d sin = n Legea Bragg permite calcularea unghiurilor la care avem maxime de difracţie pentru un set particular de plane din cristal. Intensitatea fascicolului difractat este influenţat de tipul de celulă elementară. Exemplu: Considerăm două celule elementare, a b c, = = = 90 (ce sistem, tip, câţi atomi /celulă? ) 153

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 154

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Condiţia de difracţie e dată de legea Bragg: 2 d sin = n Legea Bragg permite calcularea unghiurilor la care avem maxime de difracţie pentru un set particular de plane din cristal. Intensitatea fascicolului difractat este influenţat de tipul de celulă elementară. Exemplu: Considerăm două celule elementare, a b c, = = = 90 (ce sistem, tip, câţi atomi /celulă? ) 155

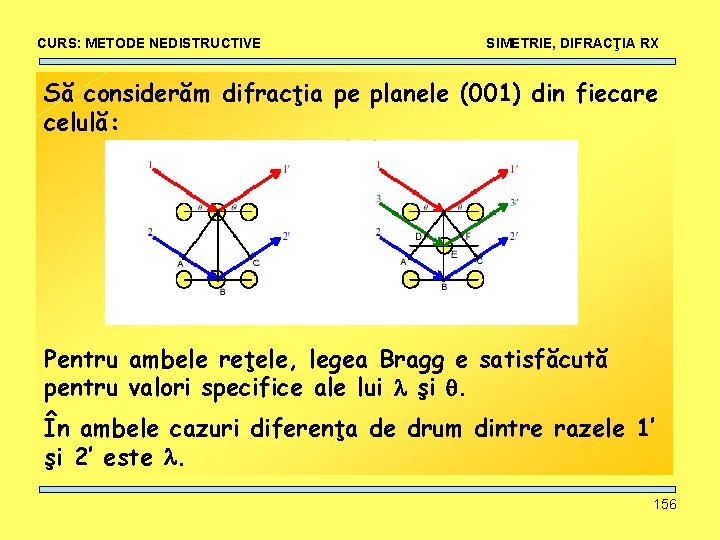
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Să considerăm difracţia pe planele (001) din fiecare celulă: Pentru ambele reţele, legea Bragg e satisfăcută pentru valori specifice ale lui şi . În ambele cazuri diferenţa de drum dintre razele 1’ şi 2’ este . 156

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Pentru celula centrată în volum diferenţa de drum dintre razele 1’ şi 3’ este /2, adică 1’ şi 3’ vor fi în opoziţie de fază = se compun distructiv. Nu va exista reflexie 001 = EXTINCŢIE ANUMITE EFLEXII LIPSESC PENTRU TIPURI DE STRUCTURI CRISTALINE. UNELE Aceste reflexii sunt interzise prin FACTORUL DE STRUCTURĂ. 157

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 158

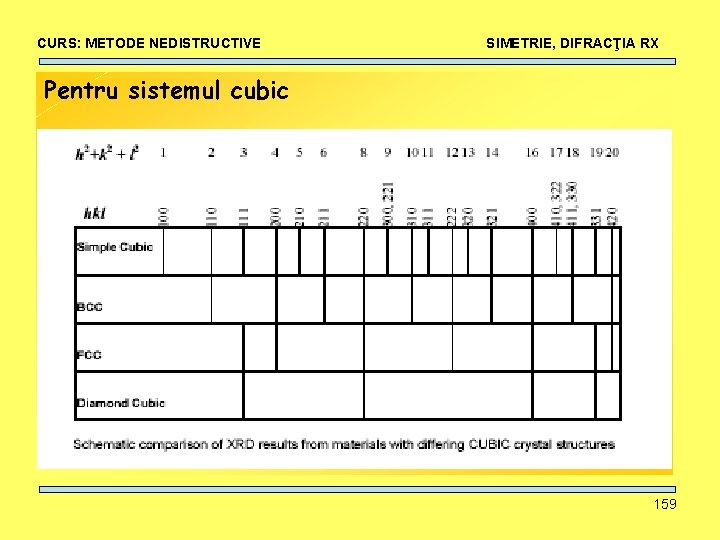
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Pentru sistemul cubic 159

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Factorul de structură descrie modul în care o bază (x, y, z) a unui tip de structură influenţează intensitatea undei împrăştiate: unde fi este factorul de împrăştiere atomică definit ca şi raportul dintre amplitudinea undei împrăştiate de un atom şi amplitudinea undei împrăştiate de un electron. Amplitudinea undei împrăştiate este proporţională cu pătratul modulului factorului de structură. 160

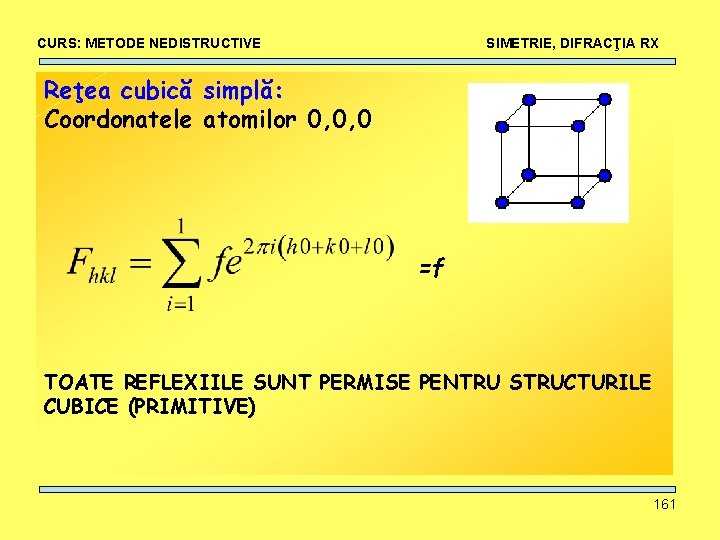
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţea cubică simplă: Coordonatele atomilor 0, 0, 0 =f TOATE REFLEXIILE SUNT PERMISE PENTRU STRUCTURILE CUBICE (PRIMITIVE) 161

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 162

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Reţea cu feţe centrate: Coordonatele atomilor: F. Dacă h, k, l sunt de acelaşi fel (adică toţi pari sau toţi impari), F = 4 f Dacă h, k, l sunt amestecaţi F = 0. 163

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 164

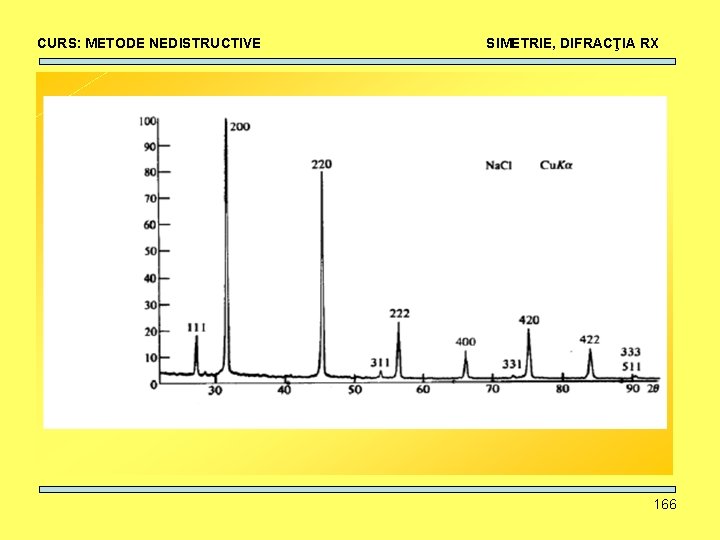
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Dar în cazul în care baza conţine mai mult de un tip de atomi? Na. Cl: Na în 0, 0, 0 + [F] Cl în 1/2, 1/2 + [F] F = 4(f. Na + f. Cl) dacă hkl pari F = 4(f. Na - f. Cl) dacă hkl impari F = 0 dacă hkl amestecaţi (la fel ca CFC) 165

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 166

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 167

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Intensitatea fasciculului difractat e dată de: unde F = factor de structură p = factor de multiplicitate e-2 M = factor de temperatură termenul dintre paranteze: Factor Polarizare-Lorentz 168

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Factorul de multiplicitate: • numărul de plane care corespund aceleiaşi reflexii. Factorul Lorentz • factorii geometrici legaţi de orientarea planelor de reflexie în cristal: intensitatea este diferită de zero pentru unghiuri care diferă puţin de unghiurile Bragg lărgirea liniilor de difracţie. Factorul de polarizare • radiaţia incidentă nu este polarizată Factorul de temperatură • Ţine cont de faptul că atomii unei reţele oscilează, termic, în jurul unor poziţii de echilibru. Cu creşterea temperaturii se modifică distanţa interplanară, scade intensitatea liniei de difracţie şi creşte fondul. 169

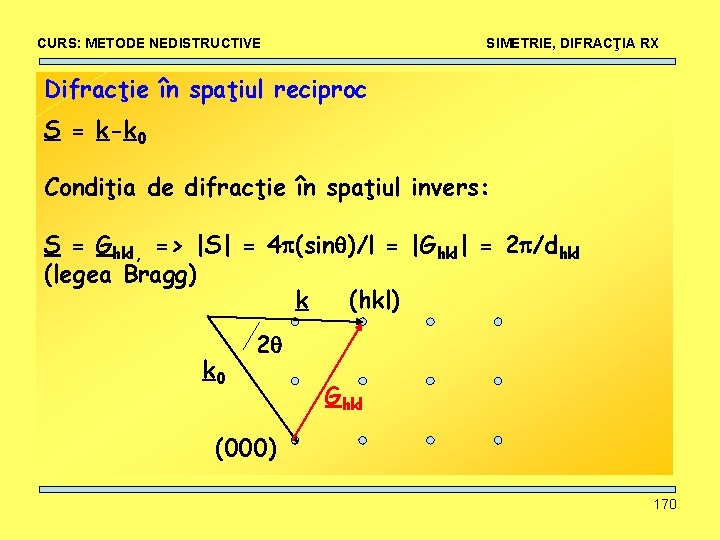
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Difracţie în spaţiul reciproc S = k-k 0 Condiţia de difracţie în spaţiul invers: S = Ghkl, => |S| = 4 (sin )/l = |Ghkl| = 2 /dhkl (legea Bragg) k (hkl) k 0 2 Ghkl (000) 170

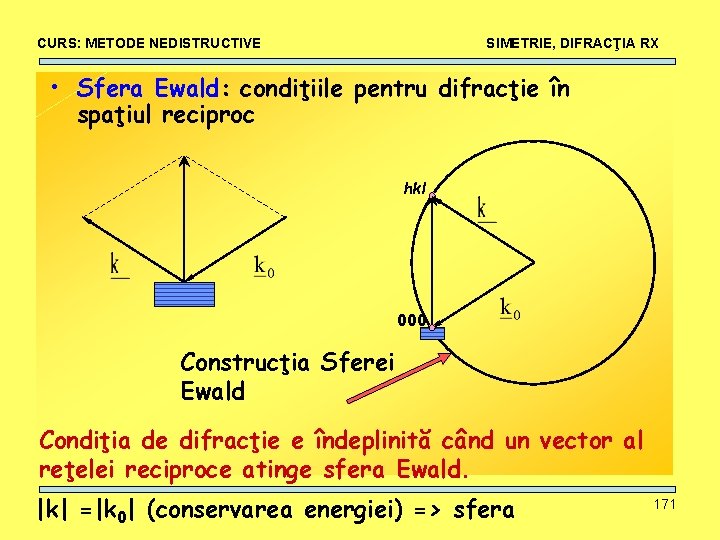
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX • Sfera Ewald: condiţiile pentru difracţie în spaţiul reciproc hkl 000 Construcţia Sferei Ewald Condiţia de difracţie e îndeplinită când un vector al reţelei reciproce atinge sfera Ewald. |k| =|k 0| (conservarea energiei) => sfera 171

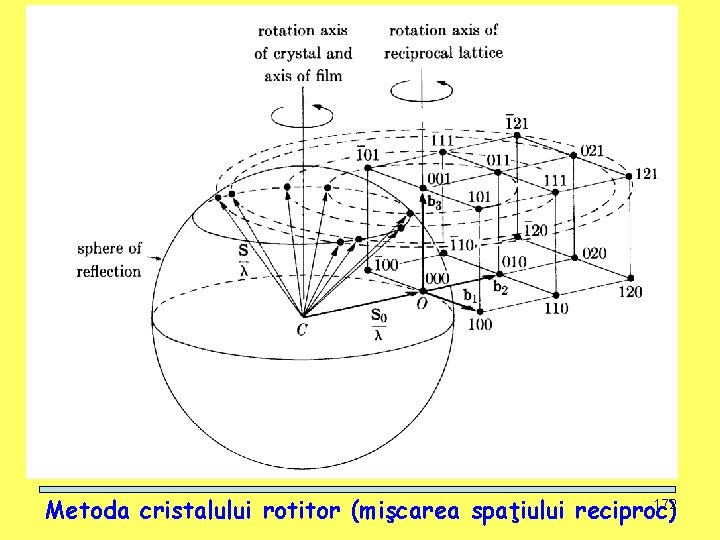
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 172 Metoda cristalului rotitor (mişcarea spaţiului reciproc)

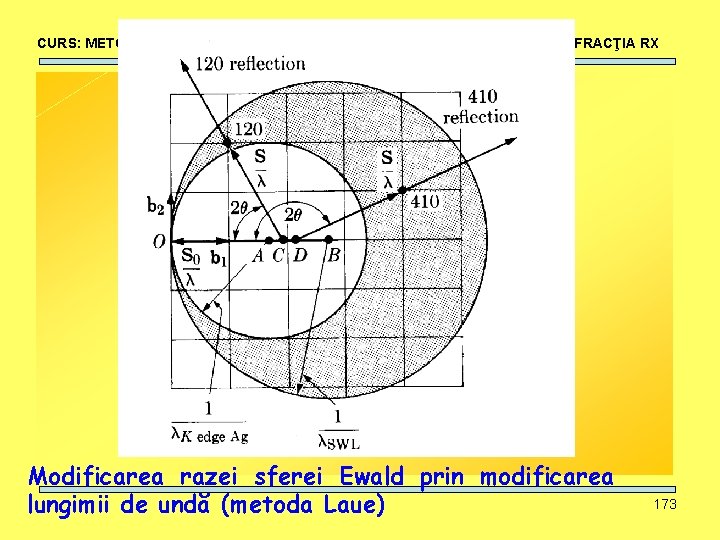
CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Modificarea razei sferei Ewald prin modificarea lungimii de undă (metoda Laue) 173

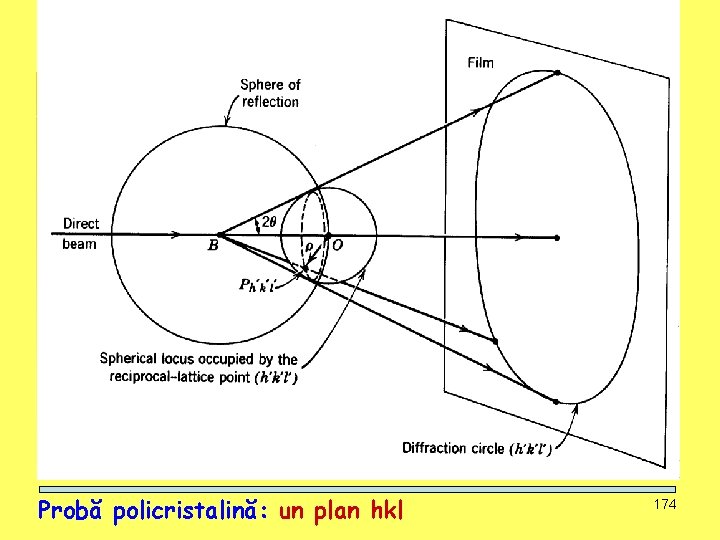
CURS: METODE NEDISTRUCTIVE Probă policristalină: un plan hkl SIMETRIE, DIFRACŢIA RX 174

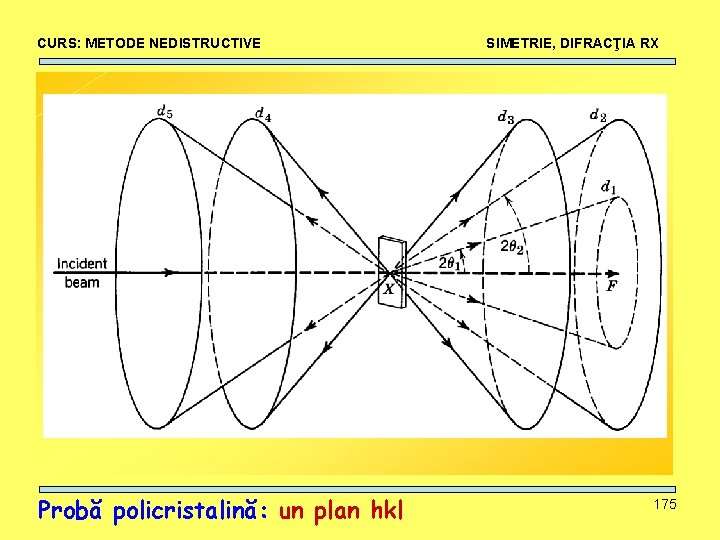
CURS: METODE NEDISTRUCTIVE Probă policristalină: un plan hkl SIMETRIE, DIFRACŢIA RX 175

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX 176

CURS: METODE NEDISTRUCTIVE SIMETRIE, DIFRACŢIA RX Metoda pulberilor Debye Scherrer 177