CurrentandResistance Electric Current Resistance and Ohms Law A

Current�and�Resistance • Electric Current • Resistance and Ohm’s Law • A Model for Electrical Conduction • Resistance and Temperature • Superconductor • Electrical Energy and Power

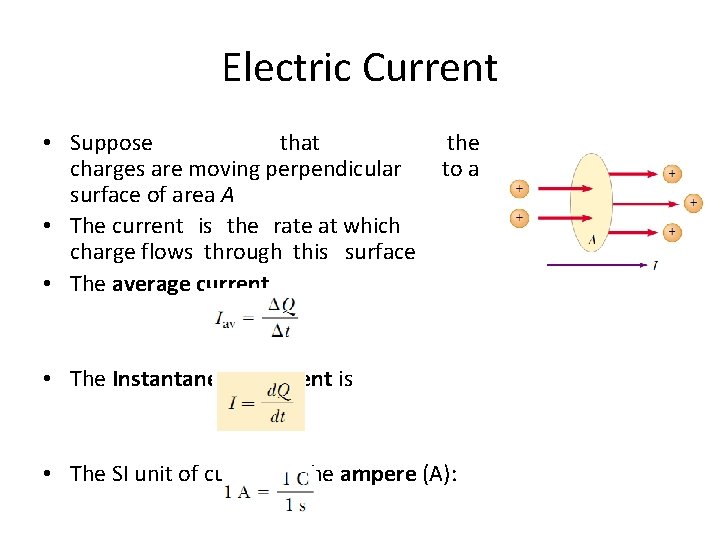
Electric Current • Suppose that charges are moving perpendicular surface of area A • The current is the rate at which charge flows through this surface • The average current the to a • The Instantaneous current is • The SI unit of current is the ampere (A):

Electric Current (2) • It is conventional to assign to the current the same direction as the flow of positive charge • In electrical conductors, the direction of the current is opposite the direction of flow of electrons • It is common to refer to a moving charge (positive or negative) as a mobile charge carrier

Microscopic Model of Current • We can relate current to the motion of the charge carriers by describing a microscopic model of conduction in a metal • The volume of a section of the conductor of length is • If n represents the number of mobile charge carriers per unit volume, the number of carriers in the gray section is • If the charge of each carrier is q, total charge in the section is

Microscopic Model of Current (2) • If the carrier moves with the speed distance during is , thus , the • The average current in the conductor is • The speed of the charge carriers vd is an average speed called the drift speed

RESISTANCE AND OHM’S LAW • We know that average current is • The current density J • In some materials, the current density is pr oportional to the electric field: • The constant is called conductivity. It is well-known as ohm’s law • Materials that obey Ohm’s law is said to be ohmic

RESISTANCE AND OHM’S LAW (2) • The potential difference between a and b is • We can rewrite the current density as • Because then the potential difference • The quantity is called the resistance R of the conductor • The unit of R is ohm (volt/ampere)

RESISTANCE AND OHM’S LAW (3) • The inverse of conductivity is resistivity

Various Resistance

A MODEL FOR ELECTRICAL CONDUCTION • This models describes the connection between resistivity and electron movement in conductor. • In absence of E, the electron moves randomly. The net movement is zero. Thus the drift velocity is zero (Fig. a) • An E modifies the random motion and causes the electrons to drift in a direction opposite that of E • The slight curvature in the paths shown in Fig. b results from the acceleration of the electrons between collisions • The acceleration of the electron is • The electron will gain velocity

A MODEL FOR ELECTRICAL CONDUCTION (2) • Suppose that vi=0 and is the average value of successive collision, then the drift velocity • The magnitude of the current density is • Comparing with ohm’s law

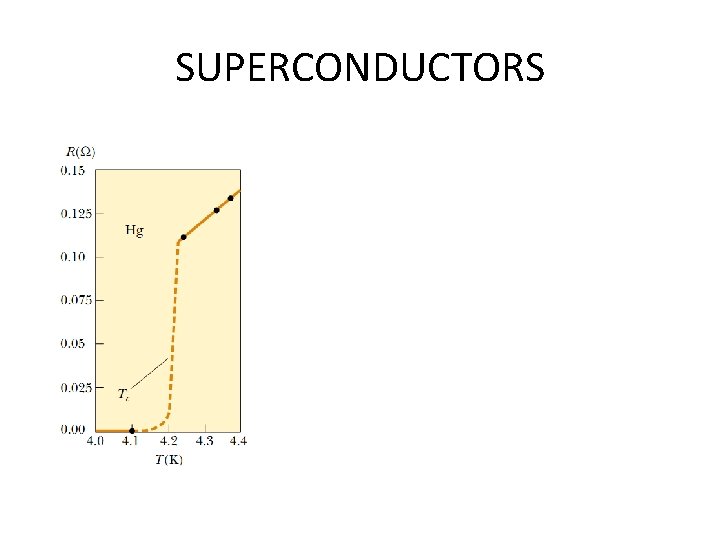
RESISTANCE AND TEMPERATURE • The resistivity of a metal varies approximately linearly with temperature according to the expression • The variation of resistance as • T 0 is normally 20 o C

SUPERCONDUCTORS

ELECTRICAL ENERGY AND POWER • When net positive charge moves from a to b, it gains electric potential energy. The chemical potential energy in battery decreases. • As the charge travels from c to d, it losses the electric potential energy due to the collision with resistor’s atom. • The rates is • The energy lost in resistor is equal energy transferred by battery

ELECTRICAL ENERGY AND POWER • The resistor’s voltage is , thus other formulas for energy in capacitor • A battery is an emf source

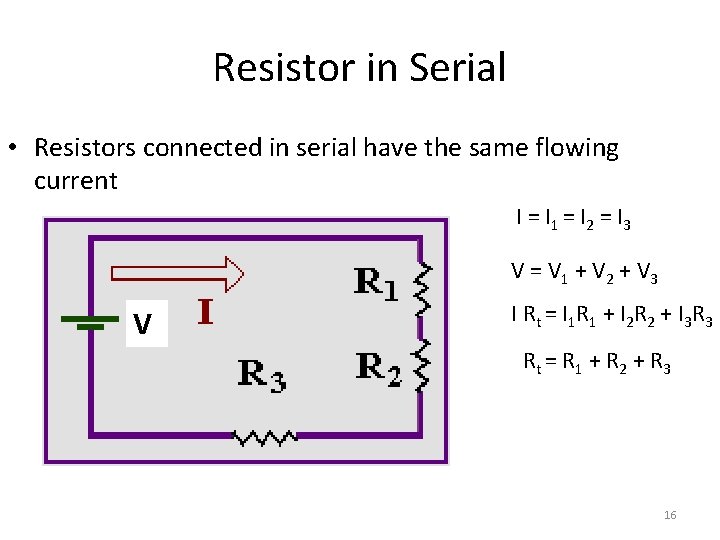
Resistor in Serial • Resistors connected in serial have the same flowing current I = I 1 = I 2 = I 3 V = V 1 + V 2 + V 3 V I R t = I 1 R 1 + I 2 R 2 + I 3 R 3 Rt = R 1 + R 2 + R 3 16

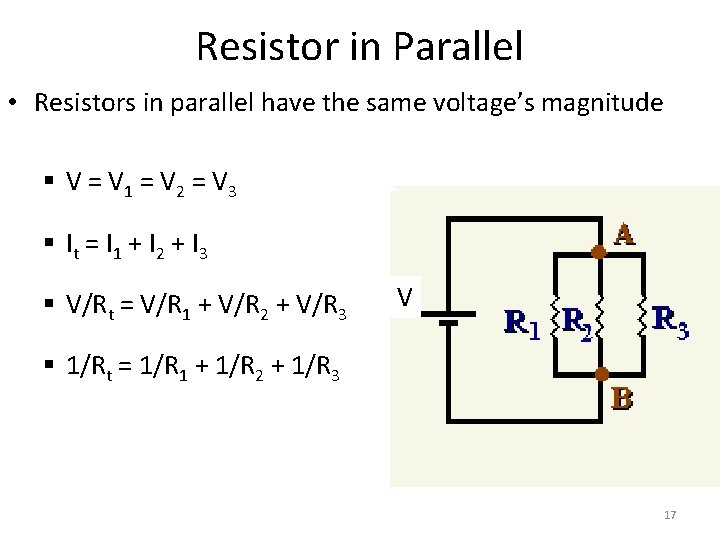
Resistor in Parallel • Resistors in parallel have the same voltage’s magnitude § V = V 1 = V 2 = V 3 § It = I 1 + I 2 + I 3 § V/Rt = V/R 1 + V/R 2 + V/R 3 V § 1/Rt = 1/R 1 + 1/R 2 + 1/R 3 17