CURE An Efficient Clustering Algorithm for Large Databases

CURE: An Efficient Clustering Algorithm for Large Databases Xuanqing Chu Zhuofu Song 1

Contents I. Background II. Problems in traditional clustering methods III. Basic idea of CURE IV. Improved CURE V. Experimental results VI. Summary VII. References 2

Background 3

Background • CURE: Clustering Using REpresentatives • A hierarchical clustering algorithm for large databases • Proposed in ‘ 98 by Guha, Rastogi and Shim 4

Background • What is Clustering? – process of grouping a set of physical or abstract objects into clusters – A cluster is a collection of data objects that are similar to one another within the same cluster and are dissimilar to the objects in other clusters – Clustering is unsupervised classification: no predefined classes 5

Background • What is Hierarchical Clustering? – A hierarchical clustering method works by grouping data objects into a tree of clusters – Further classified into agglomerative and divisive – Agglomerative hierarchical clustering is a bottom-up strategy that starts by placing each object in its own cluster, then these atomic clusters are successively merged until the number of clusters reduces to k – Divisive is the opposite: top-down – CURE is agglomerative 6

Background • How to decide which pair of clusters should merge for hierarchical clustering? – based on minimum distance – the distance between clusters can be measured as: • Mean distance: • Average distance: • Minimum distance: • Maximum distance: dmax – All of the above measures have a minimum variance flavor; usually yield the same results if clusters are compact and well separated – What if clusters close to one another (even by outliers), or their shapes are not spherical or uniform? 7

Problems in Traditional Clustering Methods 8

Problems in traditional clustering methods • Centroid-based approach (eg. uses dmean) – consider only one point as representative of a cluster: the cluster centroid – problem one: may cause a large cluster to split Figure 1: result of dmean 9

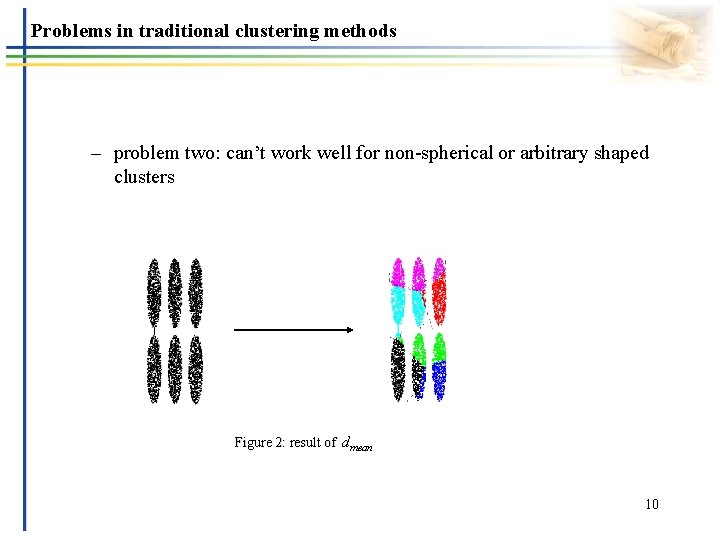
Problems in traditional clustering methods – problem two: can’t work well for non-spherical or arbitrary shaped clusters Figure 2: result of dmean 10

Problems in traditional clustering methods • All-points approach (eg. uses dmin) – consider all the points within a cluster as representatives of a cluster – problem: very sensitive to outliers and to slight changes in the position of data points Figure 3: result of dmin 11

Problems in traditional clustering methods Problems Summary • • • Traditional clustering mainly favors spherical shape Cluster size must be uniform Outliner will greatly disturb the clustering result Data points in the cluster must be compact together Each cluster must separate far away enough 12

Basic Idea of CURE Clustering 13

Basic idea of CURE clustering Introduction to CURE • Adopt middle ground approach between the centroid-based and allpoints approach • Represent each cluster by a fixed number of points that are generated by selecting well scattered points from the cluster, then shrink them toward the center of the cluster by a specified faction • Why CURE is better? – having more than one representatives allows CURE to adjust well to the geometry of non-spherical shapes – shrinking helps to dampen the effects of outliers • For metric data only: not handle categorical attributes well (see ROCK [R 2]) 14

Basic idea of CURE clustering General CURE Clustering Procedure • • Set a target representative points number c, for each cluster, select c well scattered points attempting to capture the physical shape and geometry of the cluster The chosen scattered points are then shrunk toward the centroid in a fraction of where 0 < <1 15

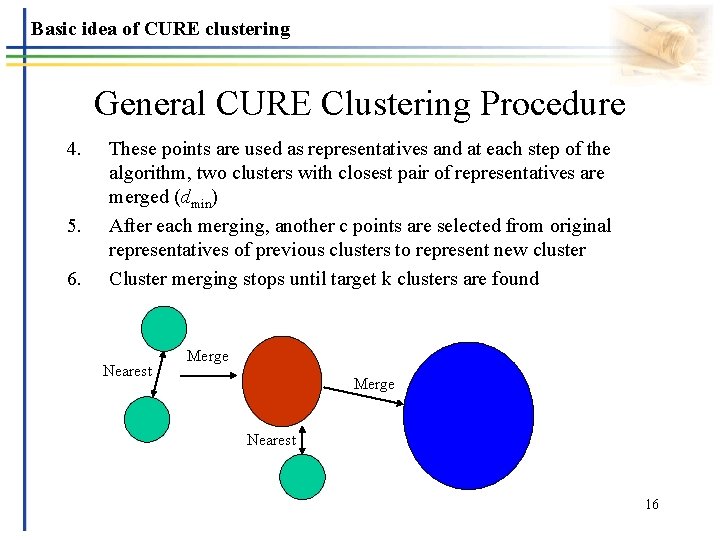
Basic idea of CURE clustering General CURE Clustering Procedure 4. 5. 6. These points are used as representatives and at each step of the algorithm, two clusters with closest pair of representatives are merged (dmin) After each merging, another c points are selected from original representatives of previous clusters to represent new cluster Cluster merging stops until target k clusters are found Nearest Merge Nearest 16

Basic idea of CURE clustering Pseudo Codes Heap: [R 3]; k-d tree: [R 4] 17

Basic idea of CURE clustering CURE Efficiency • The worst-case time complexity is O(n 2 logn) • The space complexity is O(n) due to the use of k-d tree and heap 18

Improved CURE 19

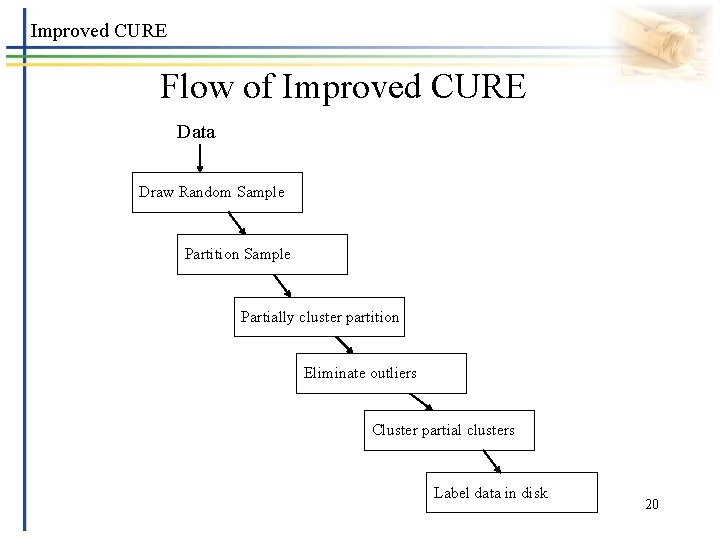
Improved CURE Flow of Improved CURE Data Draw Random Sample Partition Sample Partially cluster partition Eliminate outliers Cluster partial clusters Label data in disk 20

Improved CURE Random Sampling • Intentions – reduce data size – filter out most outliers • tradeoff between accuracy and efficiency: may miss out or incorrectly identify clusters • Why can random sampling work? – Experimental results show for most of the data sets considered, with moderate sized random samples, can obtain good clusters – Analytically, values of sample sizes for which the probability of missing clusters is low can be derived 21

Improved CURE • What should the size of the random sample be so that the probability of missing clusters is low? – Assume in order to detect a cluster u present, we need to at least capture f fraction of data from this cluster f|u| – if the sample size s satisfies then the probability that sample contains fewer than f|u| points belonging to cluster u is less than [0, 1] • How to draw the random sample? – Efficient algorithms exist for drawing a sample randomly from data in a file in one pass and using constant space [R 5] 22

Improved CURE Partitioning and Two Pass Clustering • Intention: further reduce the computational time • How to do it? – First, divide the n data point into p partitions and each contains n/p data points – Second, pre-cluster each partition until the number of clusters n/pq reaches in each partition for some q > 1 – Then, each result cluster in the first pass is used as the second pass clustering input to form the final clusters • Overall time complexity: • Overall improvement : • To maintain the quality of clustering, n/pq must be 2 to 3 times of k 23

Improved CURE Outlier Elimination • By random sampling – • most outliers are filtered out By a two-phase approach – First phase, clusters growing very slowly (eg. with 1 -2 data points) are identified and eliminated as outliners 1. this procedure is triggered when cluster number reduces to 1/3 of the original Second phase pruning occurs toward the end – 24

Improved CURE Data labeling • Due to the use of random sampling, each remaining data point needs labeling back to the proper cluster • Each data point is assigned to the cluster with a representative point closest to it 25

Experimental Results 26

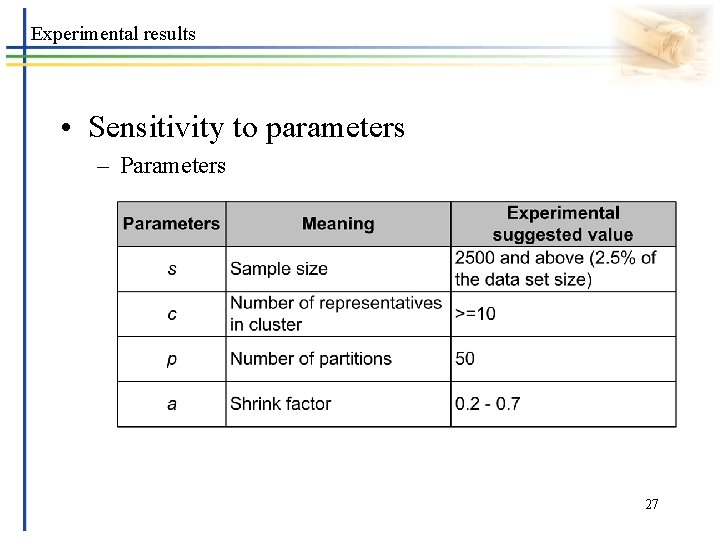
Experimental results • Sensitivity to parameters – Parameters 27

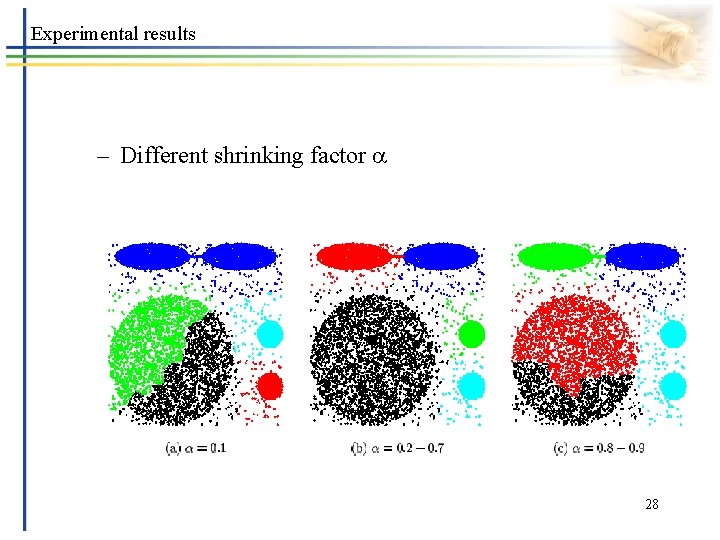
Experimental results – Different shrinking factor 28

Experimental results – Different number of representatives c 29

Experimental results • Relation of execution time, different partition number p, and different sample points s 30

Experimental results • Comparisons with BIRTH [R 6] – brief BIRTH review • BIRTH: Balanced Iterative Reducing and Clustering using Hierarchies • two concepts: clustering Feature (CF) and clustering feature tree (CF tree) – – CF = (N, LS, SS) where N: # of points; LS: linear sum of N points; SS: square sum CF tree: a height balanced tree that stores CF tree has two parameters: branching factor, B and threshold T Leaf requirement: cluster diameter or radius must be below T • two phases clustering – Phase 1: scan DB to build an initial in-memory CF tree – Phase 2: use an arbitrary clustering algorithm to cluster the leaf nodes of CF tree – BIRTH fails to identify clusters with non-spherical shapes or non-uniform sizes; while CURE succeeds 31

Summary • CURE can identify clusters having non-spherical shapes and wide variances in size with the help of well scattered representative points and centroid shrinking • CURE can handle large databases by employing a combination of random sampling and partitioning • CURE is robust to outliers • The quality and effectiveness of CURE can be tuned by varying different s, p, c, to adapt different input data sets 32

References • • • [R 1]: S. Guha, R. Rastogi, and K. Shim. CURE: An efficient clustering algorithm for large databases. In SIGMOD'98, pp. 73 -84, 1998 [R 2]: S. Guha, R. Rastogi, and K. Shim. ROCK: A robust clustering algorithm for categorical attributes. In ICDE'99, pp. 512 -521, 1999 [R 3]: Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to Algorithms. The MIT Press, Massachusetts, 1990 [R 4]: Hanan Samet. The Design and Analysis of Spatial Data Structures. Addison-Wesley Publishing Company, Inc. , New York, 1990 [R 5]: Jeff Vitter. Random sampling with a reservoir. ACM Transactions on Mathematical Software, 11(1): 37 -57, 1985 [R 6]: T. Zhang, R. Ramakrishnan, and M. Livny. BIRCH: An efficient data clustering method for very large databases. In SIGMOD'96, pp. 103 -114, 1996 33

34