CULLIDE Interactive Collision Detection Between Complex Models in

CULLIDE: Interactive Collision Detection Between Complex Models in Large Environments using Graphics Hardware Naga K. Govindaraju, Stephane Redon, Ming C. Lin, Dinesh Manocha University of North Carolina at Chapel Hill The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Problem Given a large environment with moving objects, Compute overlapping objects Overlapping triangles in each pair The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Goal Interactive collision detection between complex objects Large number of objects High primitive count Non-convex objects Open and closed objects The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Non-rigid Motion Deformable objects Changing topology The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Real-time Collision Detection using our Approach Complex breaking objects on a NVIDIA Ge. Force FX 5800 Ultra GPU The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Related Work Collision detection Hardware accelerated techniques The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Related Work Object space techniques Two phases Broad phase – Compute object pairs in close proximity Narrow phase – Check each pair for exact collision detection The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Related Work Broad phase Spatial partitioning Sweep-and-prune Narrow phase Convex objects Spatial partitioning Bounding volume hierarchies Surveys in [Klosowski 1998, Lin and Manocha 2003, Redon et al. 2002] The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Limitations of Object-space Techniques Considerable pre-processing Hard to achieve real-time performance on complex deformable models The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Collision Detection using Graphics Hardware Primitive rasterization – sorting in screen-space Interference tests The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Image Space Techniques Use of graphics hardware CSG rendering [Goldfeather et al. 1989, Rossignac et al. 1990] Interferences and cross-sections [Baciu et al. 1998, Myszkowski 1995, Rossignac et al. 1992, Shinya and Forgue 1991] Minkowski sums [Kim et al. 2001] Cloth animation [Vassilev et al. 2001] Virtual Surgery [Lombardo et al. 1999] Proximity computation [Hoff et al. 2001, 2002] The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Limitations of Current Approaches Closed models Frame buffer readbacks – slow The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

CPU, GPU and Bandwidth Growth on Consumer PCs The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
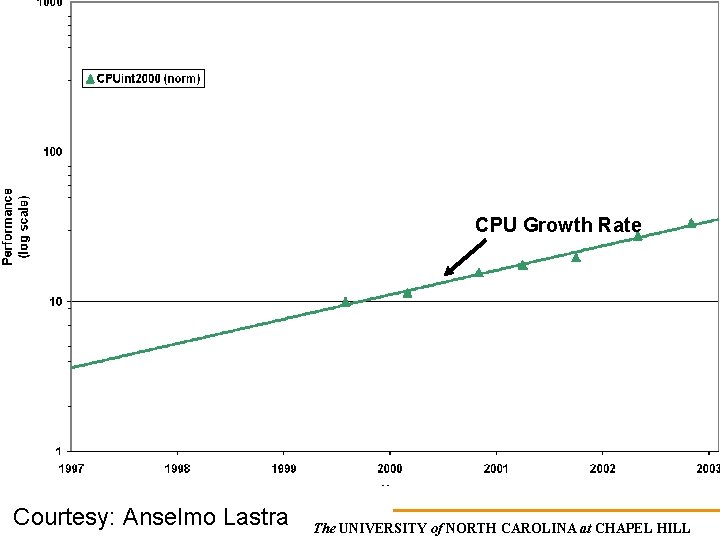
CPU Growth Rate Courtesy: Anselmo Lastra The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
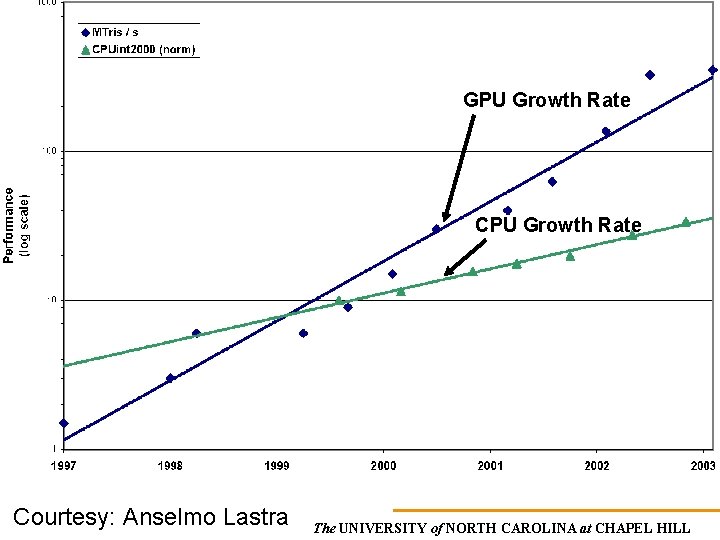
GPU Growth Rate Courtesy: Anselmo Lastra The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
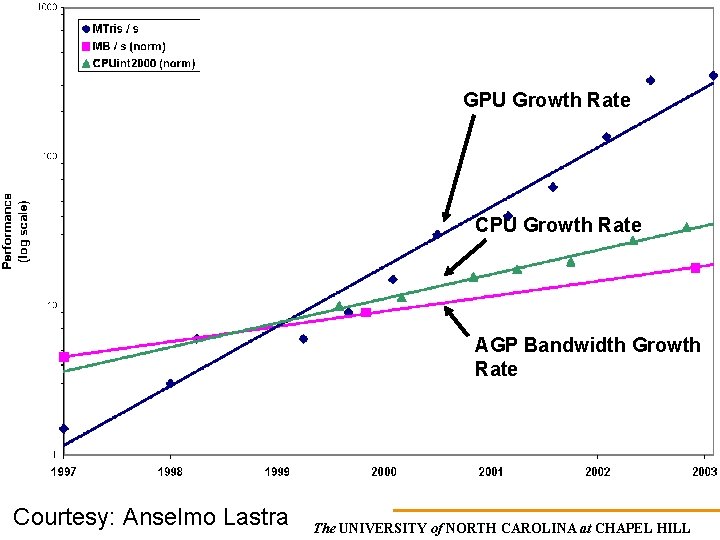
GPU Growth Rate CPU Growth Rate AGP Bandwidth Growth Rate Courtesy: Anselmo Lastra The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Readback Timings NVIDIA Ge. Force 4 Dell Precision Workstation 1 Kx 1 K depth buffer – 50 ms The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Outline Overview Pruning Algorithm Implementation and Results Conclusions and Future Work The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Outline Overview Pruning Algorithm Implementation and Results Conclusions and Future Work The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Overview Potentially Colliding Set (PCS) computation Exact collision tests on the PCS The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
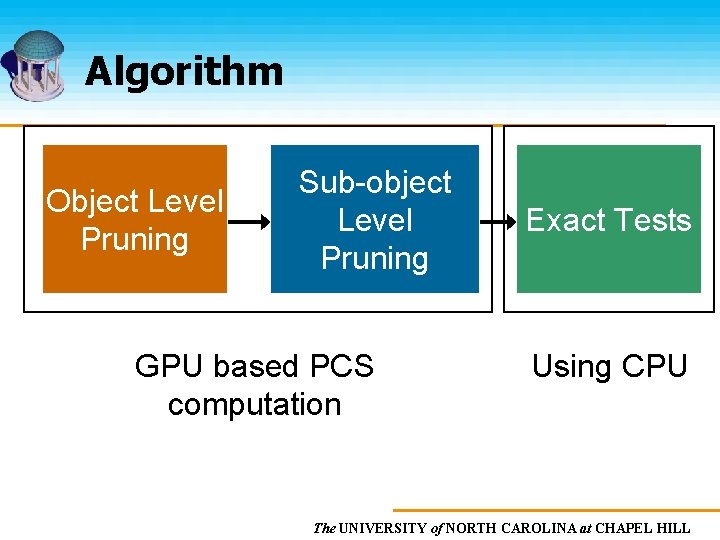
Algorithm Object Level Pruning Sub-object Level Pruning GPU based PCS computation Exact Tests Using CPU The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
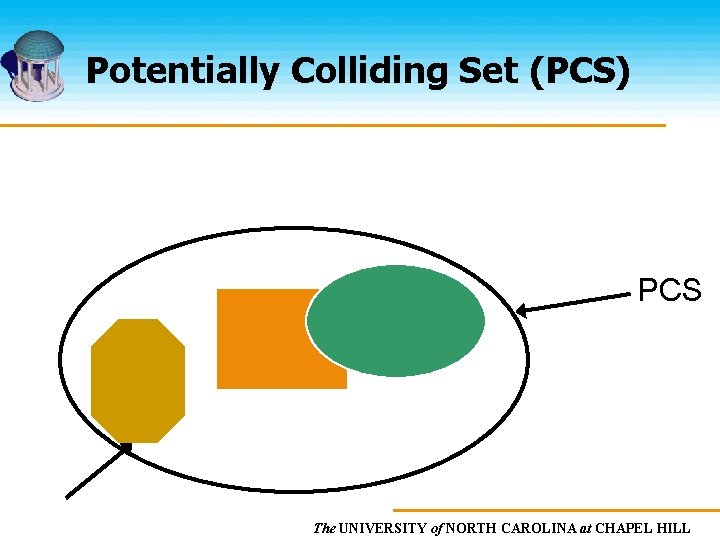
Potentially Colliding Set (PCS) PCS The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
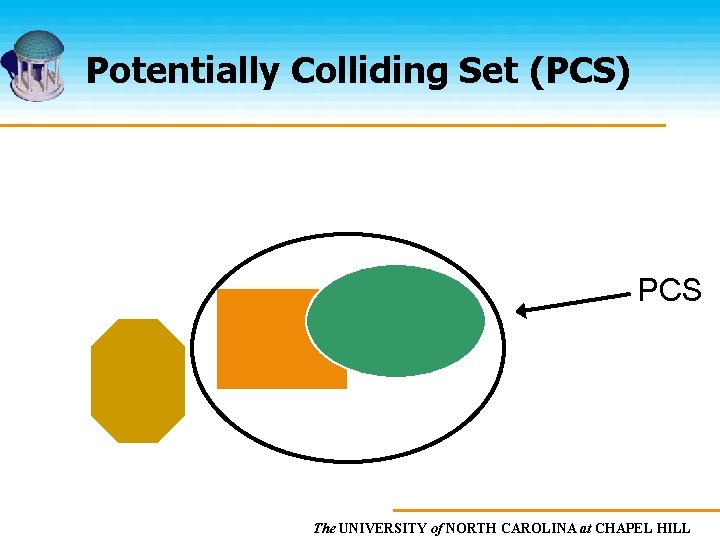
Potentially Colliding Set (PCS) PCS The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Outline Problem Overview Pruning Algorithm Implementation and Results Conclusions and Future Work The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
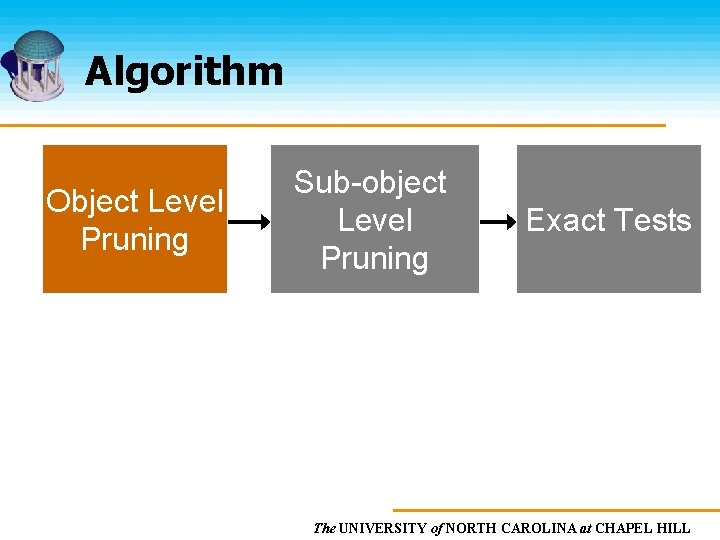
Algorithm Object Level Pruning Sub-object Level Pruning Exact Tests The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Visibility Computations Lemma 1: An object O does not collide with a set of objects S if O is fully visible with respect to S Utilize visibility for PCS computation The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
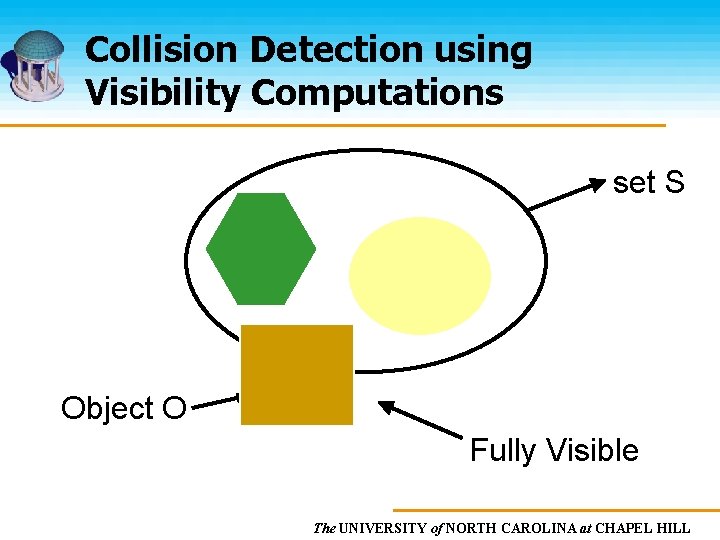
Collision Detection using Visibility Computations set S Object O Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Pruning Lemma 2: Given n objects O 1, O 2, …, On , an object Oi does not belong to PCS if it does not collide with O 1, …, Oi-1, Oi+1, …, On Prune objects that do not collide The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Pruning O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Pruning O 1 O 2 … Oi-1 Oi The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Pruning Oi Oi+1 … On-1 On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Computation Each object tested against all objects but itself Naive algorithm is O(n 2) Linear time algorithm Uses two pass rendering approach Conservative solution The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Computation: First Pass Render O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
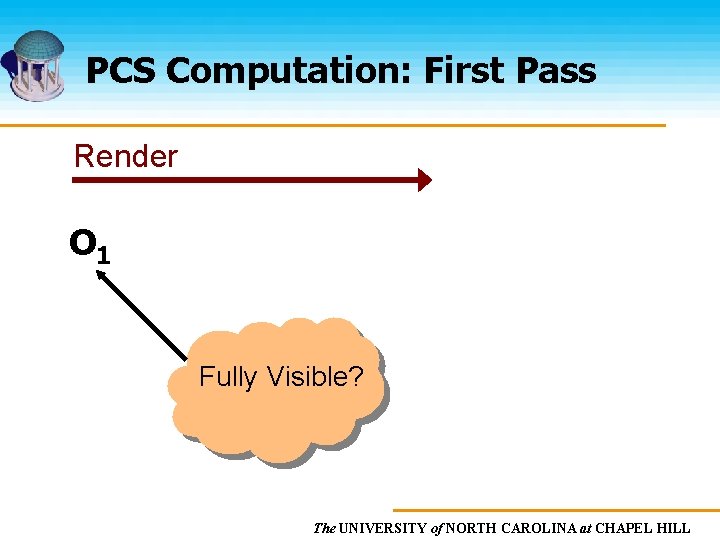
PCS Computation: First Pass Render O 1 Fully Visible? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
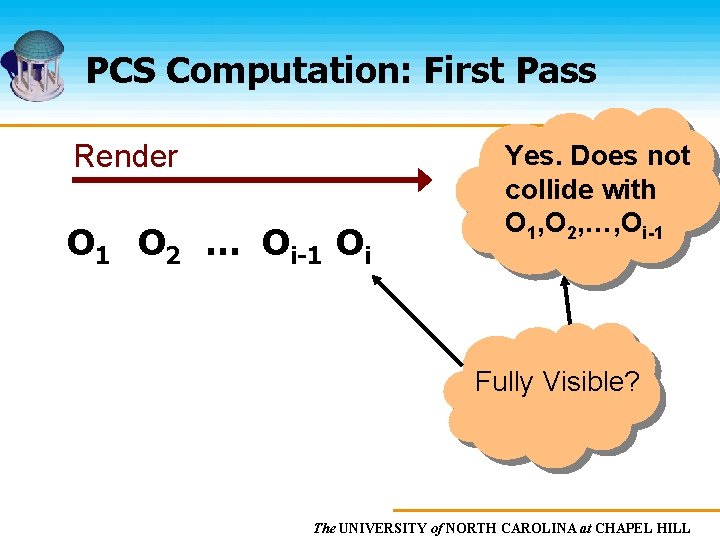
PCS Computation: First Pass Render O 1 O 2 … Oi-1 Oi Yes. Does not collide with O 1, O 2, …, Oi-1 Fully Visible? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
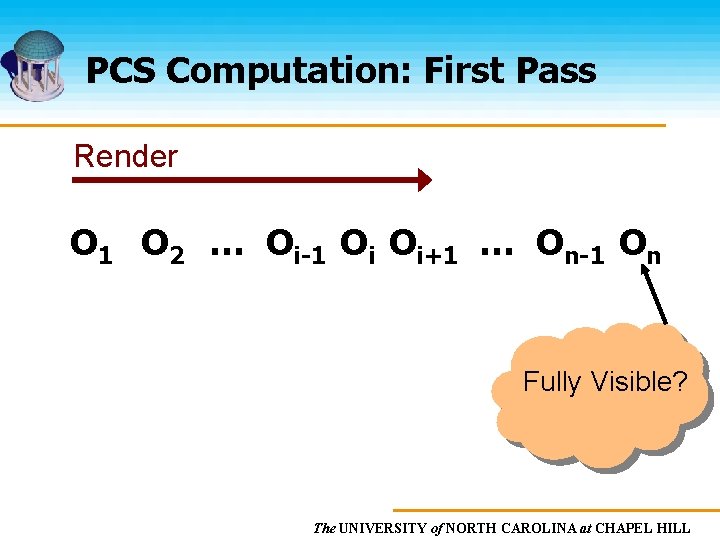
PCS Computation: First Pass Render O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On Fully Visible? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Computation: Second Pass Render O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
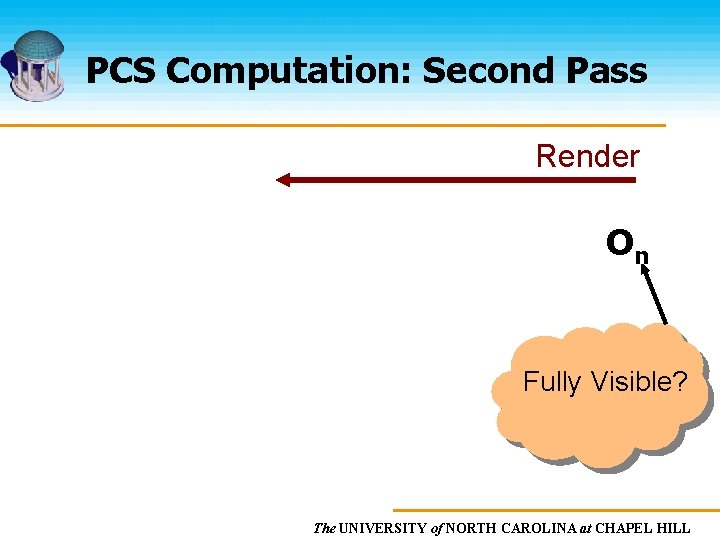
PCS Computation: Second Pass Render On Fully Visible? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
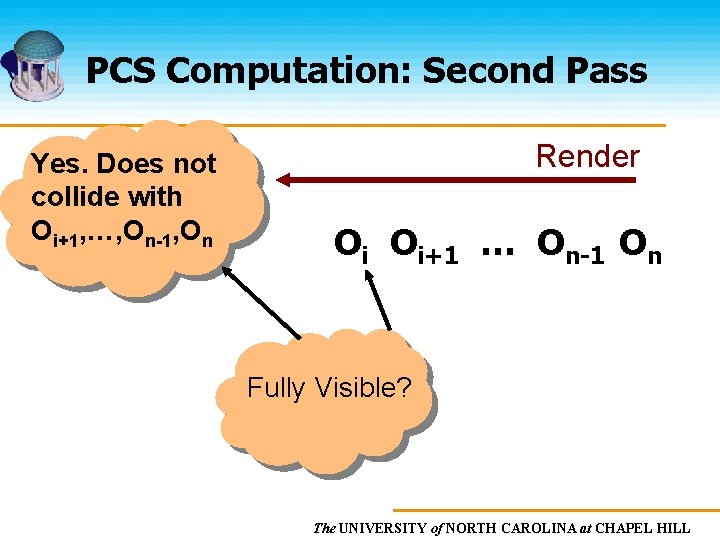
PCS Computation: Second Pass Yes. Does not collide with Oi+1, …, On-1, On Render Oi Oi+1 … On-1 On Fully Visible? The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
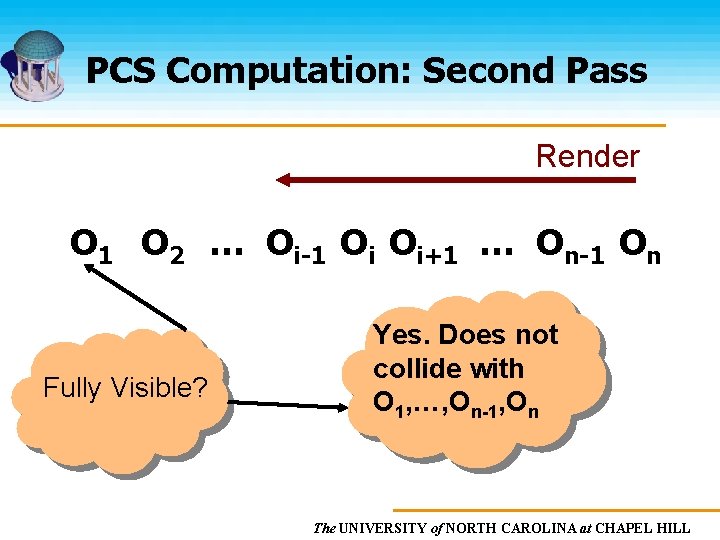
PCS Computation: Second Pass Render O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On Fully Visible? Yes. Does not collide with O 1, …, On-1, On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

PCS Computation Fully Visible O 1 O 2 … Oi-1 Oi Oi+1 … On-1 On The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
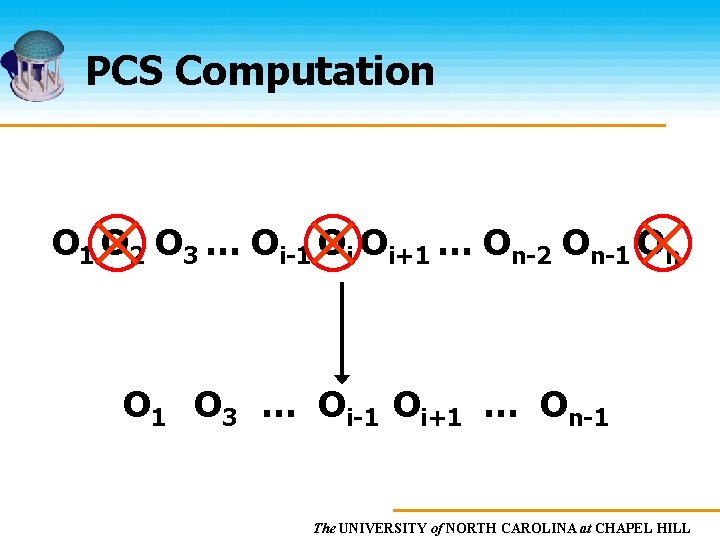
PCS Computation O 1 O 2 O 3 … Oi-1 Oi Oi+1 … On-2 On-1 On O 1 O 3 … Oi-1 Oi+1 … On-1 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
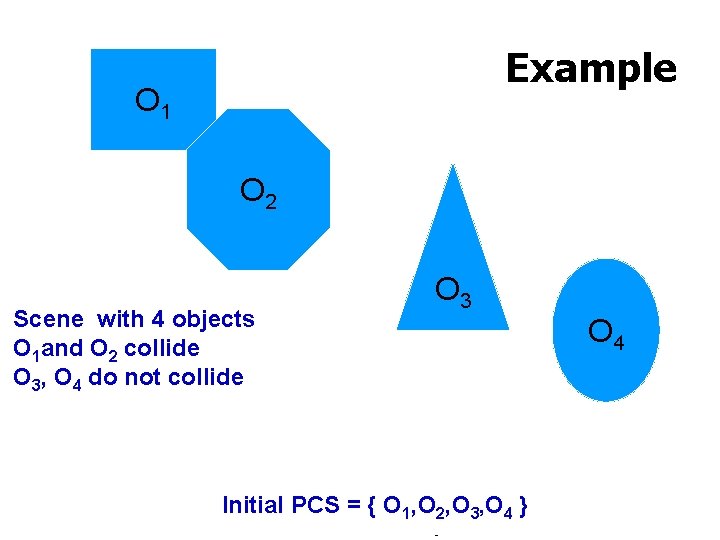
Example O 1 O 2 Scene with 4 objects O 1 and O 2 collide O 3, O 4 do not collide O 3 O 4 Initial PCS = { O 1, O 2, O 3, O 4 } The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
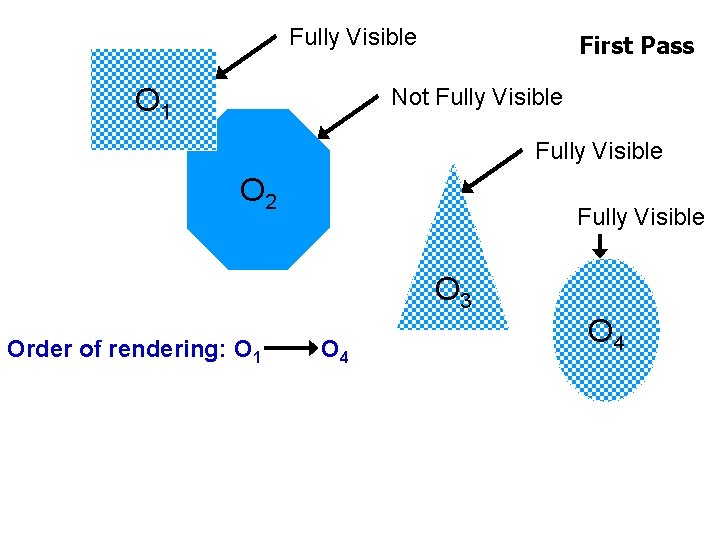
Fully Visible O 1 First Pass Not Fully Visible O 2 Fully Visible O 3 Order of rendering: O 1 O 4 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
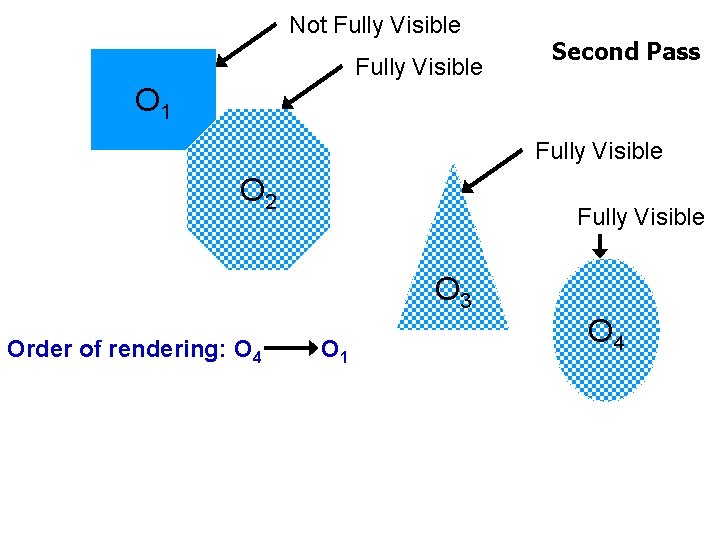
Not Fully Visible Second Pass O 1 Fully Visible O 2 Fully Visible O 3 Order of rendering: O 4 O 1 O 4 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
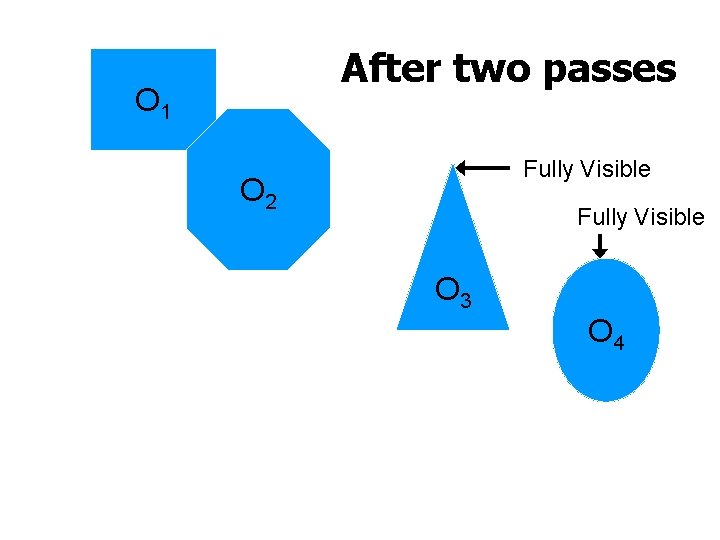
After two passes O 1 Fully Visible O 2 Fully Visible O 3 O 4 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
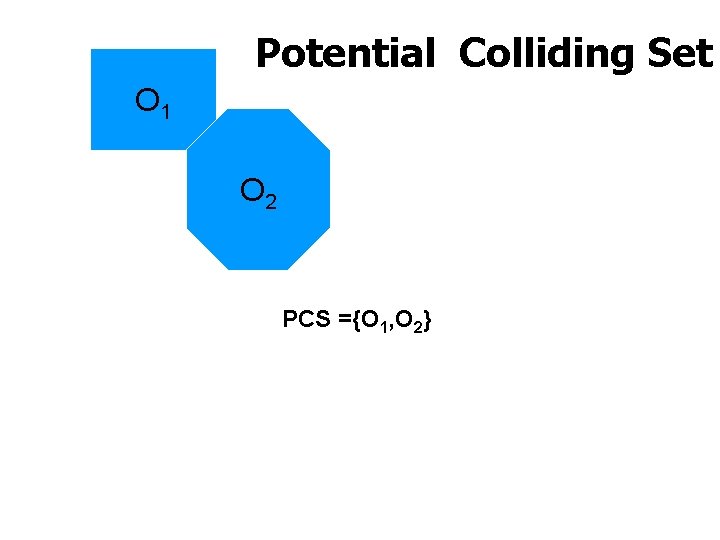
Potential Colliding Set O 1 O 2 PCS ={O 1, O 2} The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Algorithm Object Level Pruning Sub-object Level Pruning Exact Tests The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Overlap Localization Each object is composed of subobjects We are given n objects O 1, …, On Compute sub-objects of an object Oi that overlap with sub-objects of other objects The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Overlap Localization Our solution Test if each sub-object of Oi overlaps with sub -objects of O 1, . . Oi-1 Test if each sub-object of Oi overlaps with sub -objects of Oi+1, . . . , On Linear time algorithm Extend the two pass approach The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
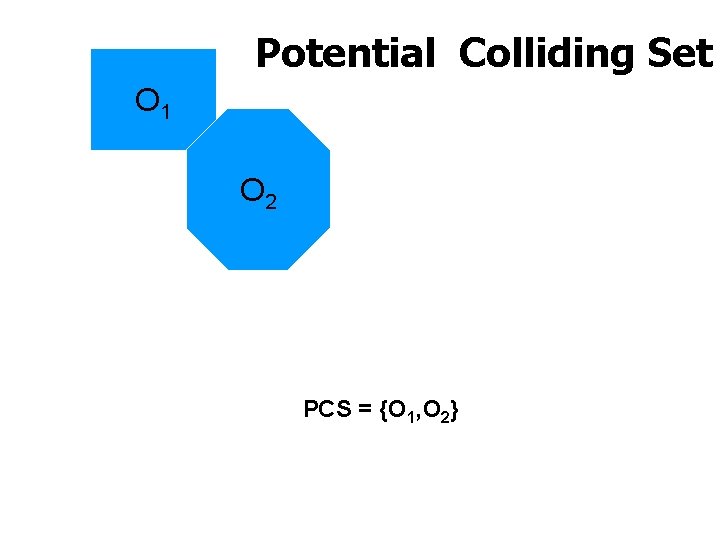
Potential Colliding Set O 1 O 2 PCS = {O 1, O 2} The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
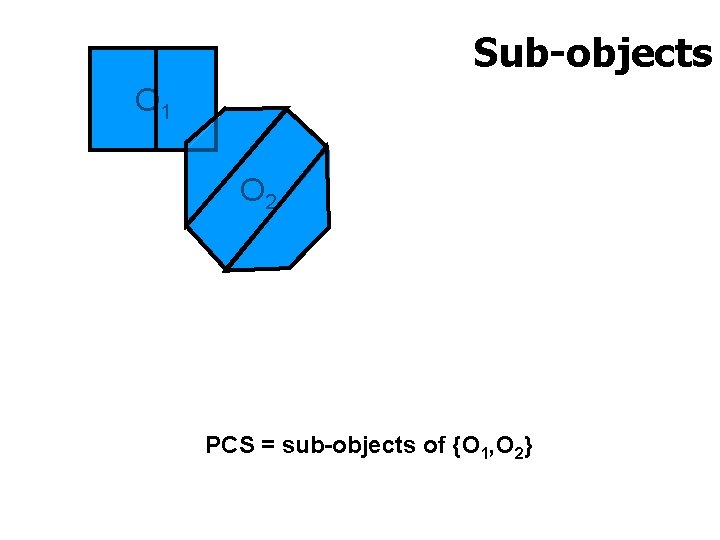
Sub-objects O 1 O 2 PCS = sub-objects of {O 1, O 2} The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

First Pass Rendering order: Sub-objects of O 1 O 2 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
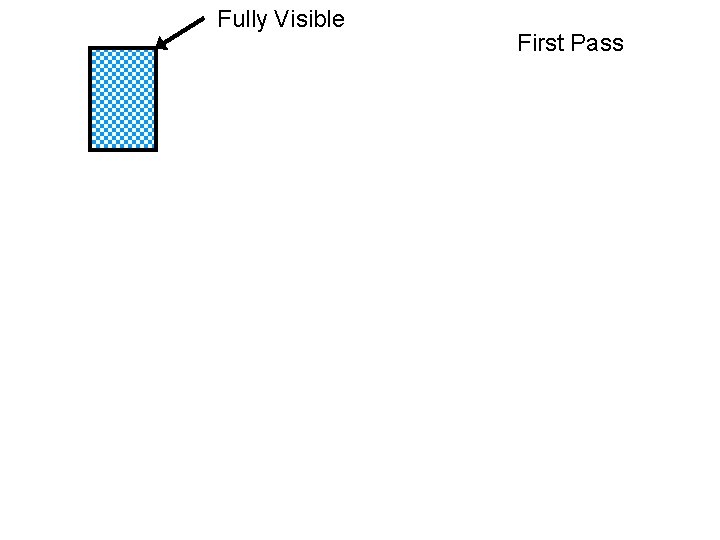
Fully Visible First Pass The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
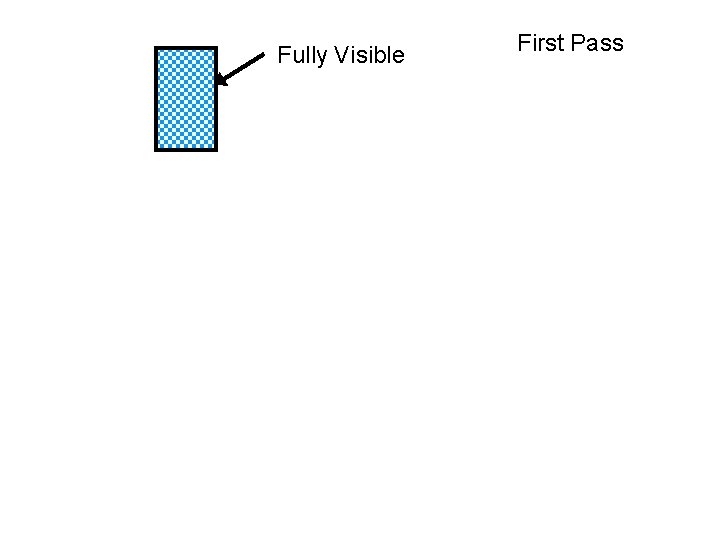
Fully Visible First Pass The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
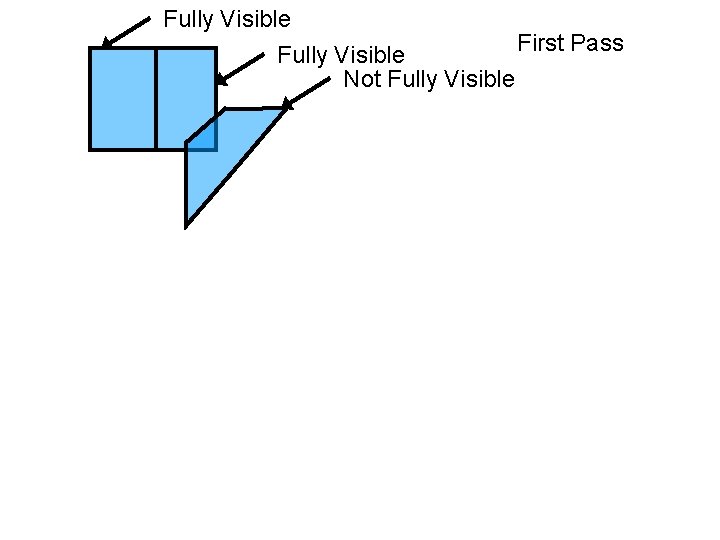
Fully Visible First Pass Fully Visible Not Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
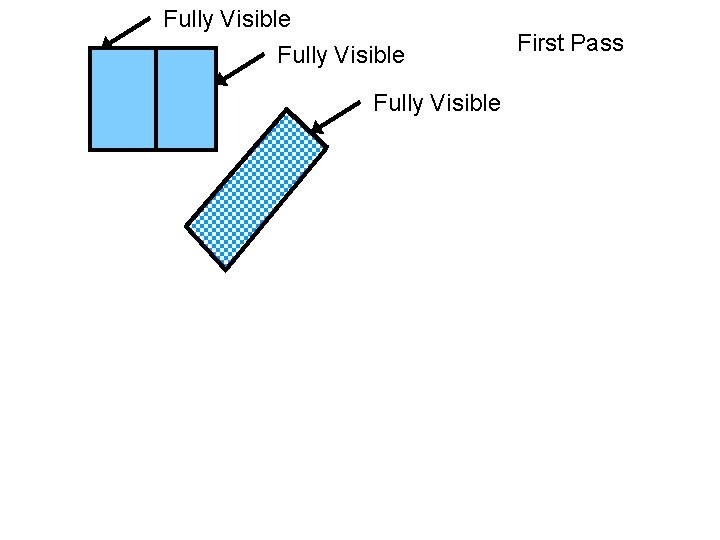
Fully Visible First Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
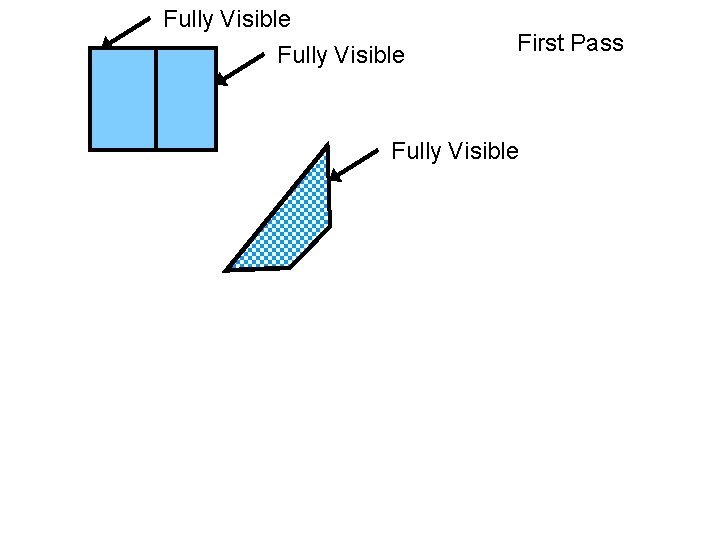
Fully Visible First Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Fully Visible First Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Second Pass Rendering order: Sub-objects of O 2 O 1 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Second Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Second Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
Second Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
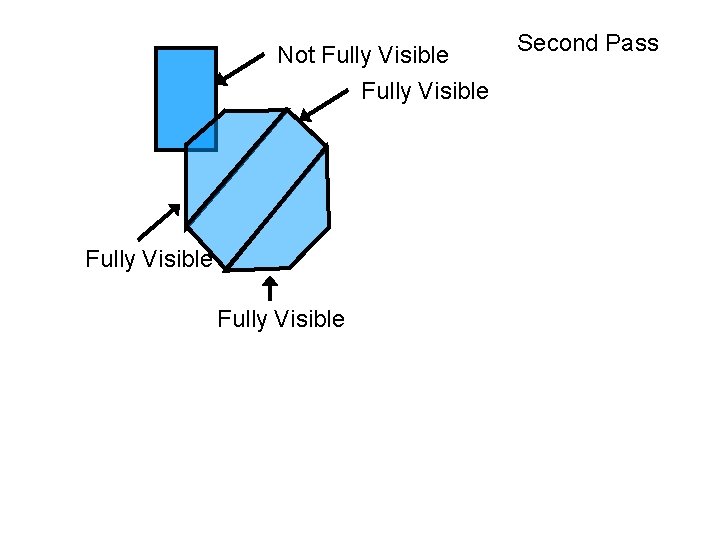
Not Fully Visible Second Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
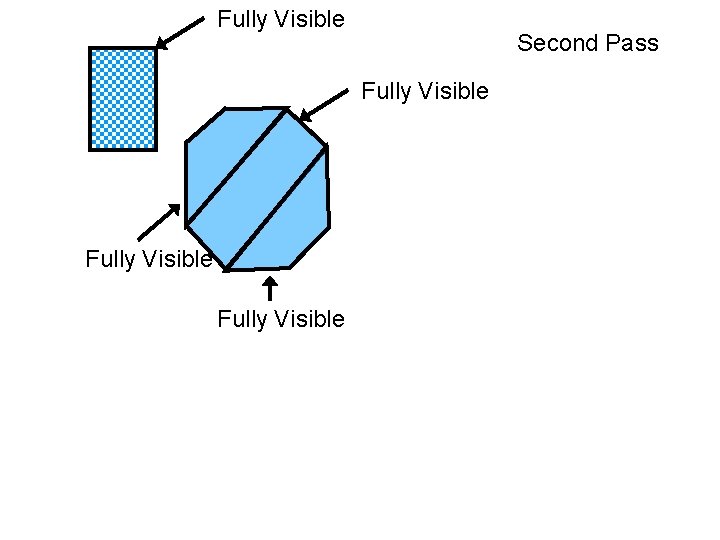
Fully Visible Second Pass Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
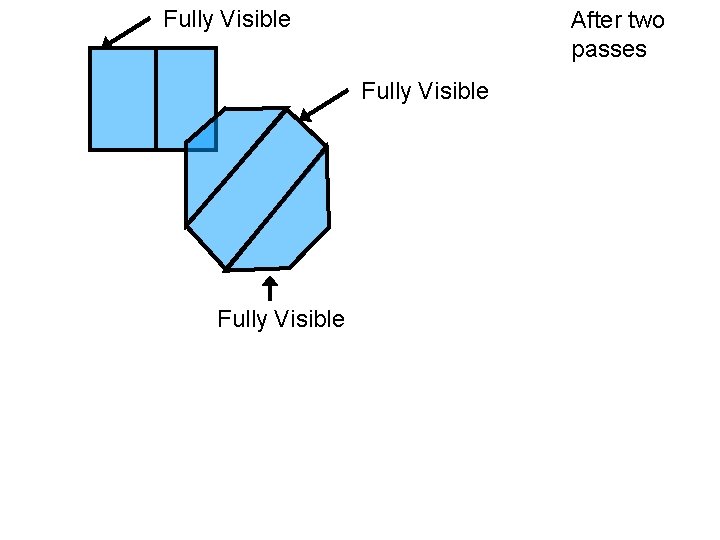
Fully Visible After two passes Fully Visible The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
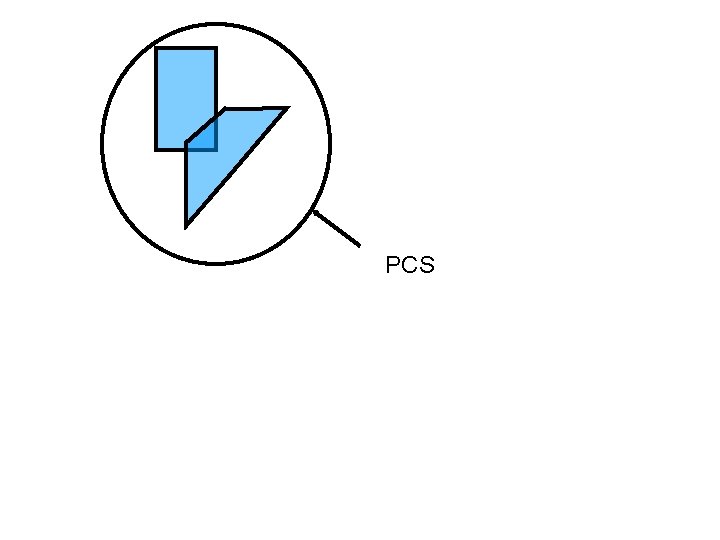
PCS The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
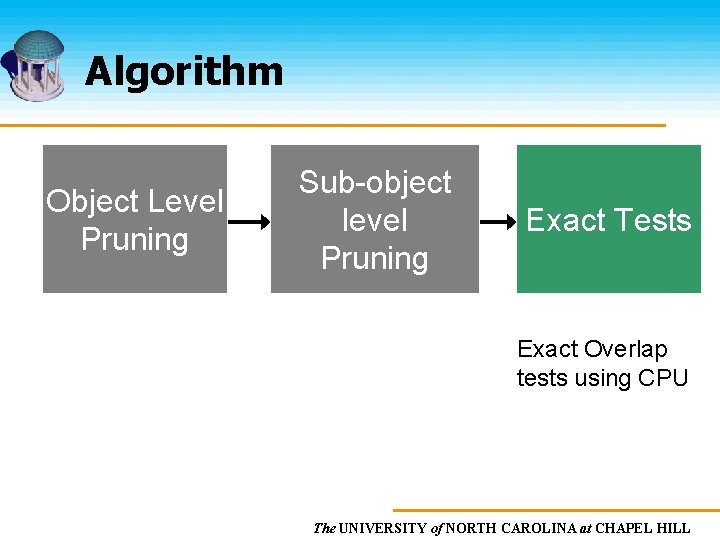
Algorithm Object Level Pruning Sub-object level Pruning Exact Tests Exact Overlap tests using CPU The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Visibility Queries We require a query Tests if a primitive is fully visible or not Current hardware supports occlusion queries Test if a primitive is visible or not Our solution Change the sign of depth function The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Visibility Queries All fragments Depth function GEQUAL LESS Pass Fail Pass Occlusion query Query not supported Examples - HP_Occlusion_test, NV_occlusion_query The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Bandwidth Analysis Read back only integer identifiers Independent of screen resolution The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Optimizations First use AABBs as object bounding volume Use orthographic views for pruning Prune using original objects The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Outline Overview Pruning Algorithm Implementation and Results Conclusions and Future Work The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Implementation Dell Precision workstation Dell M 50 Laptop The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Test Models: Environment 1 100 deforming cylinders Total – 20 K triangles The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Test Models: Environment 2 Deforming torii Each torus – 20 K triangles The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Test Model: Environment 3 250 K Dragon 35 K Bunny The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Test Model: Environment 4 Breaking dragon – 250 K triangles Bunny – 35 K triangles The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Implementation Dell Precision workstation, 2. 4 GHz Pentium IV CPU, NVIDIA Ge. Force FX 5800 Ultra GPU, 2 GB memory running Windows 2000 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
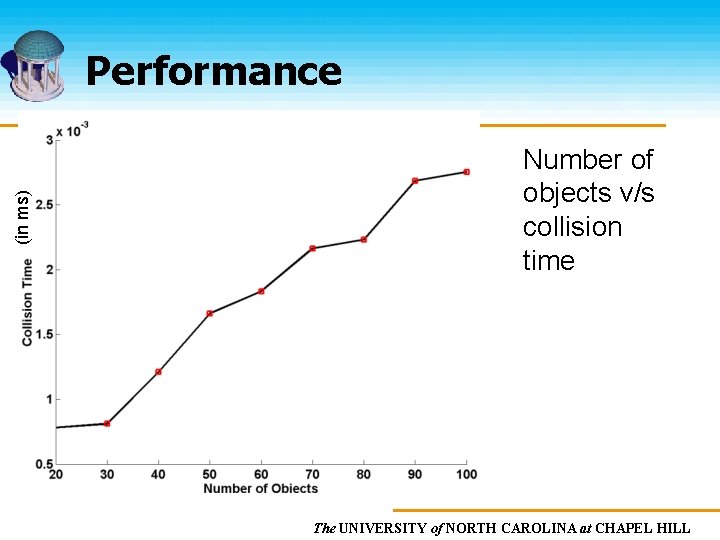
(in ms) Performance Number of objects v/s collision time The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
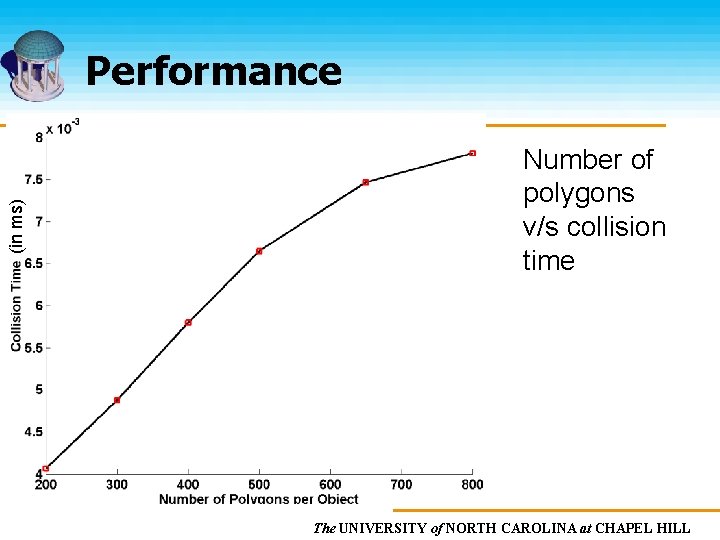
(in ms) Performance Number of polygons v/s collision time The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
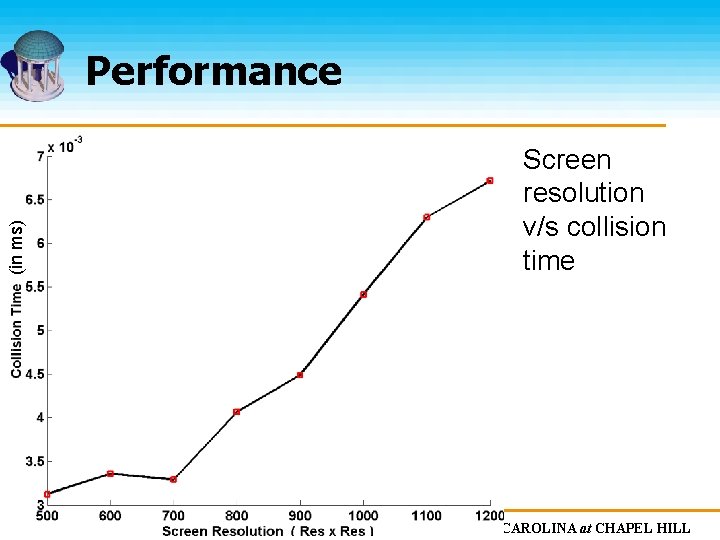
(in ms) Performance Screen resolution v/s collision time The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Advantages No coherence No assumptions on motion of objects Works on generic models A fast pruning algorithm No frame-buffer readbacks The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Limitations No distance or penetration depth information Resolution issues No self-collisions Culling performance varies with relative configurations The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Live Demo of Environment 4 Dell M 50 laptop, 2. 4 GHz Pentium IV-M CPU, NVIDIA Quadro 4 700 Go. GL GPU, 1 GB memory running Windows XP The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Live Demo of Environment 1 Avg. frames per second = 300 The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Conclusions Novel algorithm for collision detection using graphics hardware Applicable to polygon soups No assumptions on motion Linear time PCS computation algorithm No frame buffer readbacks The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Conclusions First practical solution for general deformable models and breaking objects The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Future Work Handle self-collisions Apply to more interactive applications Distance and penetration depth computation The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Acknowledgements Army Research Office National Science Foundation Office of Naval Research Intel Corporation NVIDIA Corporation Stanford Graphics Laboratory UNC GAMMA Group The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL

Questions? More info: http: //gamma. cs. unc. edu/CULLIDE E-mail: naga@cs. unc. edu The UNIVERSITY of NORTH CAROLINA at CHAPEL HILL
- Slides: 91