CUDA Linear Equations Solver Based on Modified Gaussian

CUDA Linear Equations Solver Based on Modified Gaussian By Xinggao Xia Elimination and Jong Chul Lee

Applications of Systems of Linear Equations v Biology v Physics v Chemistry

n : the number of elements in matrix Technique Additions Multiplications/Divisions Gauss-Jordan n 3/2 Gaussian Elimination n 3/3 Cramer’s Rule n 4/3 Table 1: Computational Complexity of Various Solving Techniques Comments: ØComputational complexity increases tremendously as the dimension of matrix increases. ØGaussian Elimination solver has obvious advantage in terms of complexity as the matrix

Iteration No. 1 Iteration No. 2 Iteration No. 3 Normalization Iteration No. 1 1 0 : 0 0 0 Iteration No. 2 1 0 : 0 0 0 1 0 : 0 0 …… …… Iteration No. N 1 0 : 0 0 0 1 0 : 0 0 1 : 0 1 0 : 0 1
![Inter-iteration parallelism For Iteration i A[j][]=A[j][] –m[j][i]*matrix pivot row Multiplier array m must be Inter-iteration parallelism For Iteration i A[j][]=A[j][] –m[j][i]*matrix pivot row Multiplier array m must be](http://slidetodoc.com/presentation_image/503dc9fcc7db72d9da9f57e14190a171/image-5.jpg)
Inter-iteration parallelism For Iteration i A[j][]=A[j][] –m[j][i]*matrix pivot row Multiplier array m must be determined before each iteration m 0 m 1 i m 2 i m 3 i i 1 0 : 0 0 0 Perfectly fit CUDA architecture

ØModified Gaussian Elimination is considered for CUDA linear equations solver ØMore parallelism ØNo back substitution ØPartial pivoting guarantees accuracy of solution
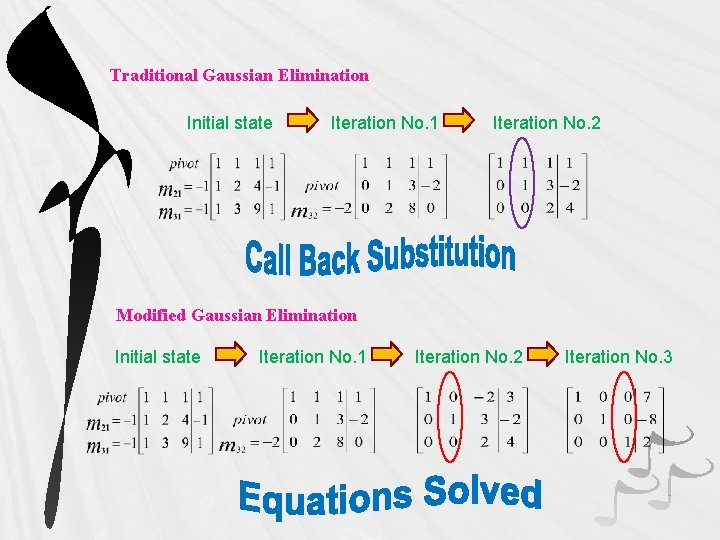
Traditional Gaussian Elimination Initial state Iteration No. 1 Iteration No. 2 Modified Gaussian Elimination Initial state Iteration No. 1 Iteration No. 2 Iteration No. 3
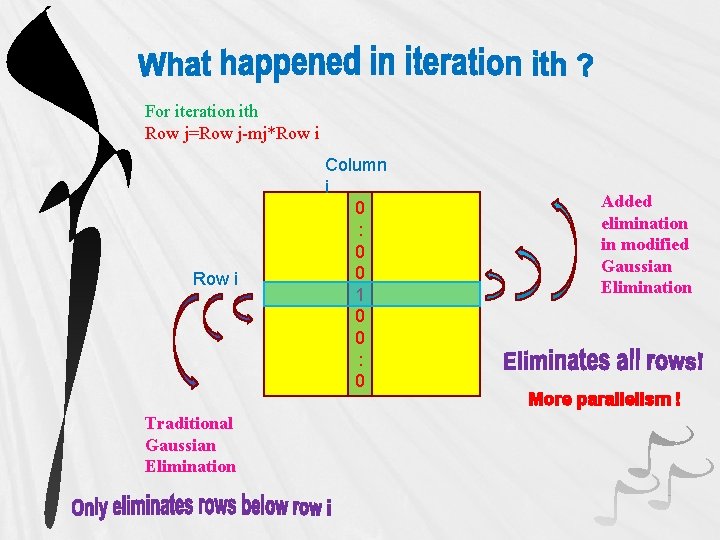
For iteration ith Row j=Row j-mj*Row i Traditional Gaussian Elimination Column i 0 : 0 0 1 0 0 : 0 Added elimination in modified Gaussian Elimination More parallelism !

Back Substitutio n Gaussian Elimination Iteration No. 1 1 0 : 0 0 0 Iteration No. 2 1 0 : 0 0 0 1 0 : 0 0 …… 1 0 : …… 0 0 0 Iteration No. N-1 1 0 : 0 0 1 : 0 1 0 : 0 11 Traditional Gaussian Linear Solver Modified Gaussian Elimination Iteration No. 1 1 0 : 0 0 0 Iteration No. 2 1 0 : 0 0 …… 1 0 : …… 0 0 0 Iteration No. N 0 1 0 : 0 1 1 : 0 0 : : 0 1 0 0 : : : 0 1 Modified Gaussian Linear Solver

For (i=0; i<N; i++) { Partial pivoting { Transfer the ith column back to host; Search the maximum of this column and return the index; (Host) Switches rows if necessary; (Device) } Determine the multiplier column; (Device) Modified Gaussian elimination; (Device) } Normalize the solution; (Device) Transfer solution back to host; Threads Architecture Ø Matrix handling like modified Gaussian Elimination kernel, each thread handles an operation of A[j][i]=A[j][i]-mj*A[i][j] for iteration ith, use two dimensional grid and block, total of N*N threads in the kernel Ø Row or column handling like partial pivoting and others, each thread for one elements in the row or column, use one dimentsional grid and block, total of N threads in the kernel
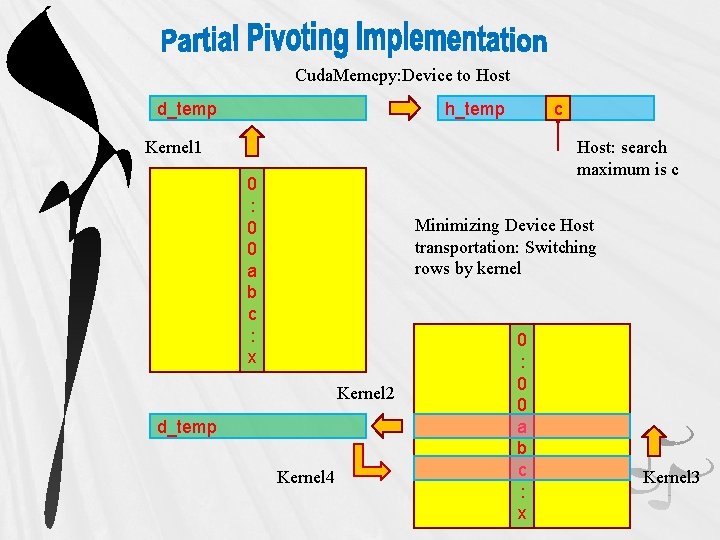
Cuda. Memcpy: Device to Host d_temp h_temp c Kernel 1 Host: search maximum is c 0 : 0 0 a b c : x Minimizing Device Host transportation: Switching rows by kernel Kernel 2 d_temp Kernel 4 0 : 0 0 a b c : x Kernel 3
![For ith iteration Each thread handles: A[j][i]=A[j][i]-mj*A[i][j] N Iteration i data partitioning B(0, 0) For ith iteration Each thread handles: A[j][i]=A[j][i]-mj*A[i][j] N Iteration i data partitioning B(0, 0)](http://slidetodoc.com/presentation_image/503dc9fcc7db72d9da9f57e14190a171/image-12.jpg)
For ith iteration Each thread handles: A[j][i]=A[j][i]-mj*A[i][j] N Iteration i data partitioning B(0, 0) B(1, 1) …… B(N-1, 1) T(0, 0) T(0, 1) ………………T(0, M 1) : : : B(i, j) B(0, N-1) Row i Column i 0 : 0 0 1 0 0 : 0 T(0, 0) T(0, 1) : : : : T(0, M-1) BLOCK_SIZE N B(0, 1) BLOCK_SIZE
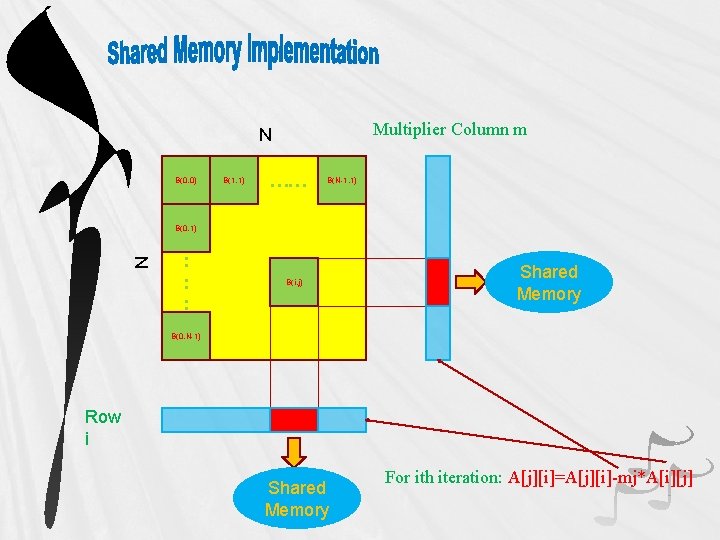
Multiplier Column m N B(0, 0) B(1, 1) …… B(N-1, 1) N B(0, 1) : : : B(i, j) Shared Memory B(0, N-1) Row i Shared Memory For ith iteration: A[j][i]=A[j][i]-mj*A[i][j]
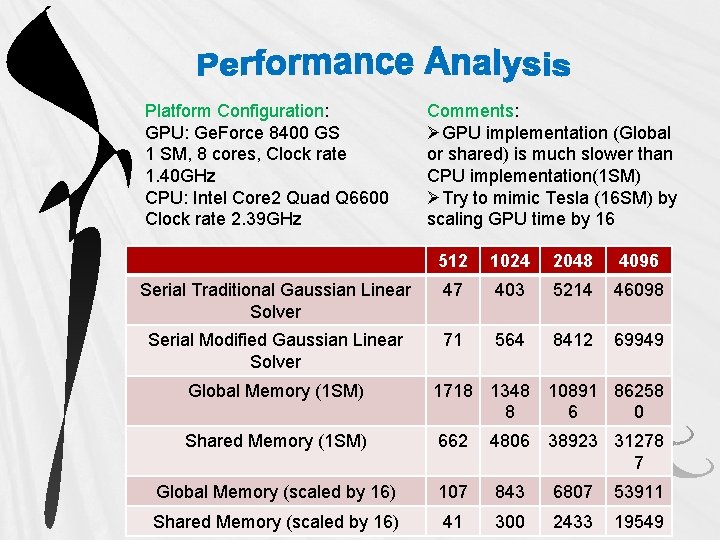
Platform Configuration: GPU: Ge. Force 8400 GS 1 SM, 8 cores, Clock rate 1. 40 GHz CPU: Intel Core 2 Quad Q 6600 Clock rate 2. 39 GHz Comments: ØGPU implementation (Global or shared) is much slower than CPU implementation(1 SM) ØTry to mimic Tesla (16 SM) by scaling GPU time by 16 512 1024 2048 4096 Serial Traditional Gaussian Linear Solver 47 403 5214 46098 Serial Modified Gaussian Linear Solver 71 564 8412 69949 Global Memory (1 SM) 1718 1348 10891 86258 8 6 0 Shared Memory (1 SM) 662 4806 38923 31278 7 Global Memory (scaled by 16) 107 843 6807 53911 Shared Memory (scaled by 16) 41 300 2433 19549
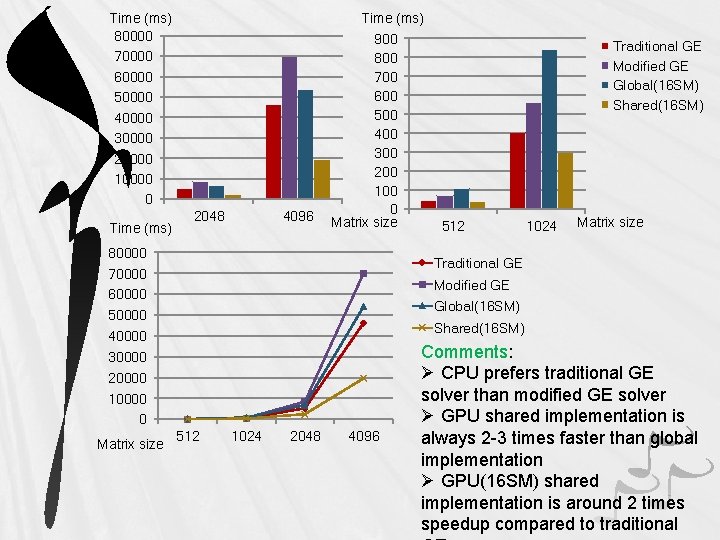
Time (ms) 80000 70000 60000 50000 40000 30000 20000 10000 0 Time (ms) 2048 4096 Time (ms) 900 800 700 600 500 400 300 200 100 0 Matrix size 80000 70000 60000 50000 40000 30000 20000 10000 0 Matrix size Traditional GE Modified GE Global(16 SM) Shared(16 SM) 512 1024 2048 4096 Comments: Ø CPU prefers traditional GE solver than modified GE solver Ø GPU shared implementation is always 2 -3 times faster than global implementation Ø GPU(16 SM) shared implementation is around 2 times speedup compared to traditional

For 1024 case (1 SM), global memory implementation time is 13488 ms, shared implementation is 4806 ms Method #Calls GPU(usec ) %GPU time Global GE_kernel 1024 1. 3 e+07 99. 11 Share d GE_kernel 1024 4. 8 e+06 97. 6 gld uncoalesced gld coalesced %uncoalesced rate Global 1048576 131072 89 Share d 61440 73728 45

Conclusion: ØLinear equations solver based on modified Gaussian Elimination is implemented on CUDA ØShared memory is about 3 times faster than global memory implementation ØShared memory is expected about 3 times faster than traditional Gaussian Elimination Solver serial code in 16 SM GPU ØPartial pivoting guarantees stability and accuracy. (error less than 0. 001 compared to serial code) Problem found: ØMore uncoalesced global memory accessing offsets advantages gained from more parallelism in modified Gaussian Elimination.
- Slides: 17