Cubical Marching Squares Adaptive Feature Preserving Surface Extraction
Cubical Marching Squares: Adaptive Feature Preserving Surface Extraction from Volume Data Chien-Chang Ho, Fu-Che Wu, Bing-Yu Chen, Yung-Yu Chuang, Ming Ouhyoung National Taiwan University
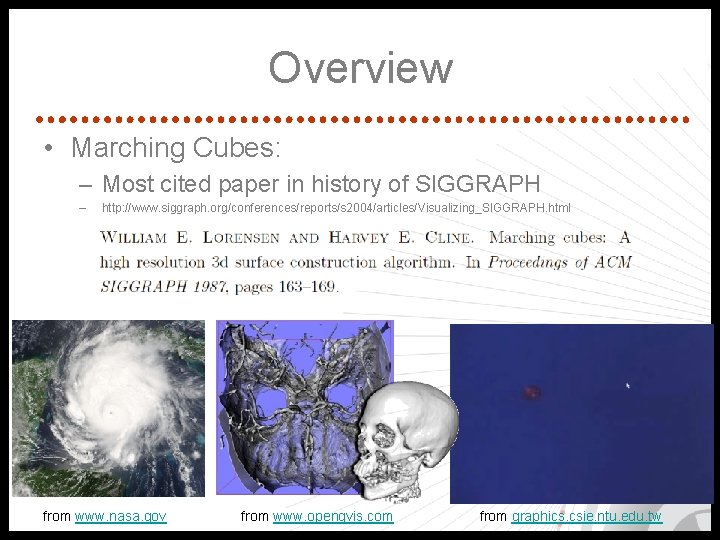
Overview • Marching Cubes: – Most cited paper in history of SIGGRAPH – http: //www. siggraph. org/conferences/reports/s 2004/articles/Visualizing_SIGGRAPH. html from www. nasa. gov from www. openqvis. com from graphics. csie. ntu. edu. tw
Problems Sharp Features Real-time Consistent Topology Adaptive Resolution
Outline Previous work & Problems Solutions Results & Conclusions
Previous work & Problems Solutions Results & Conclusions
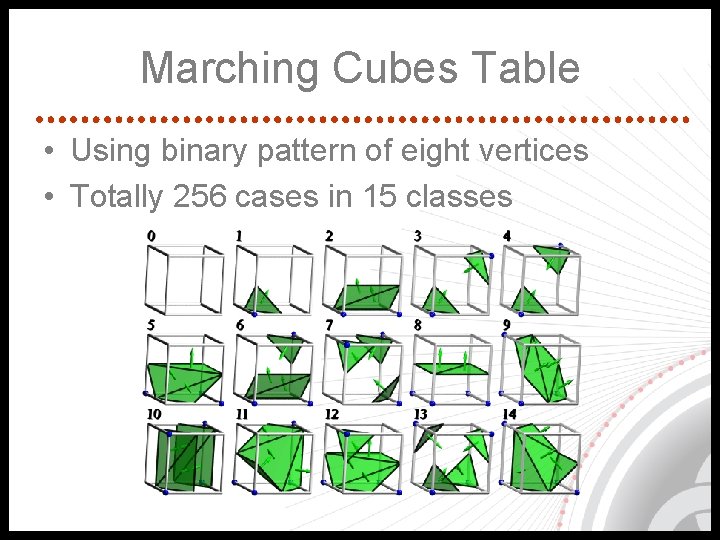
Marching Cubes Table • Using binary pattern of eight vertices • Totally 256 cases in 15 classes
Surface extraction from volume data
![Consistent topology • Ambiguity problems – [NIELSON G. M. , HAMANN B. 1991] –](http://slidetodoc.com/presentation_image_h2/f733a75d419e87b7e8ae3928e15f9765/image-8.jpg "Consistent topology • Ambiguity problems – [NIELSON G. M. , HAMANN B. 1991] –")
Consistent topology • Ambiguity problems – [NIELSON G. M. , HAMANN B. 1991] – [NATARAJAN B. K. , 1994] – [CHERNYAEV E. , 1995], etc. Consistent Topology
![Adaptive resolution – [WILHELMS J. , GELDER A. V. , 1992] – [SHU R.](http://slidetodoc.com/presentation_image_h2/f733a75d419e87b7e8ae3928e15f9765/image-9.jpg "Adaptive resolution – [WILHELMS J. , GELDER A. V. , 1992] – [SHU R.")
Adaptive resolution – [WILHELMS J. , GELDER A. V. , 1992] – [SHU R. et al, 1995], etc. Adaptive Resolution
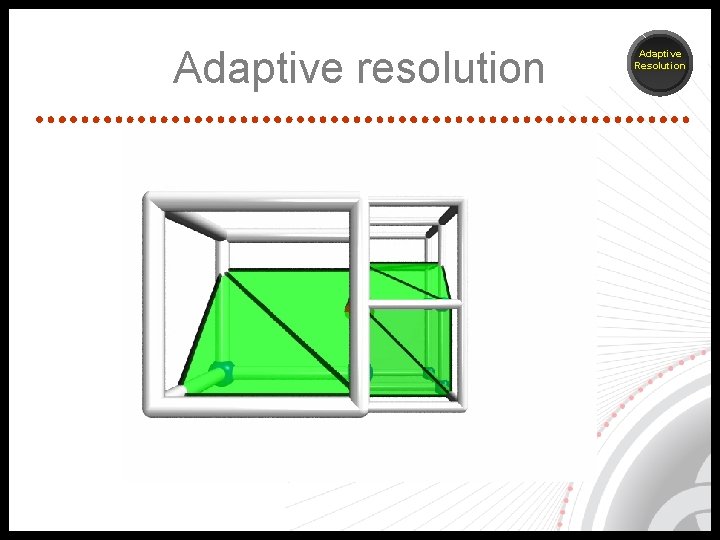
Adaptive resolution Adaptive Resolution
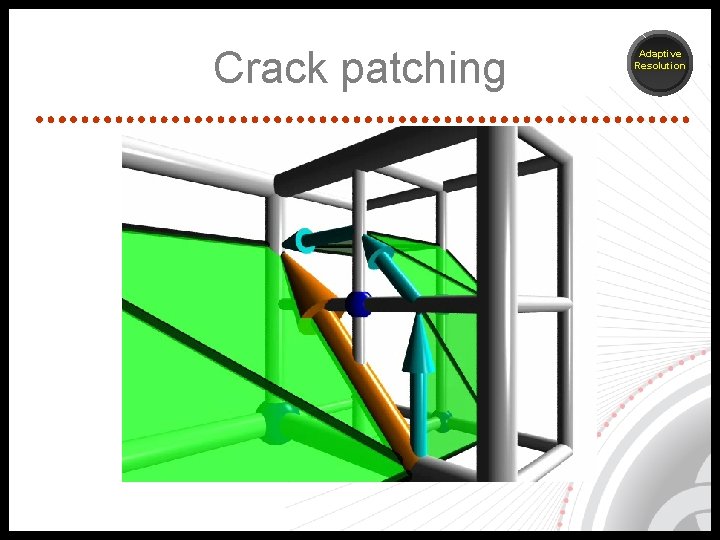
Crack patching Adaptive Resolution
![Sharp feature – [KOBBELT L. P. et al, 2001] – [JU T. et al,](http://slidetodoc.com/presentation_image_h2/f733a75d419e87b7e8ae3928e15f9765/image-12.jpg "Sharp feature – [KOBBELT L. P. et al, 2001] – [JU T. et al,")
Sharp feature – [KOBBELT L. P. et al, 2001] – [JU T. et al, 2002] Sharp Features
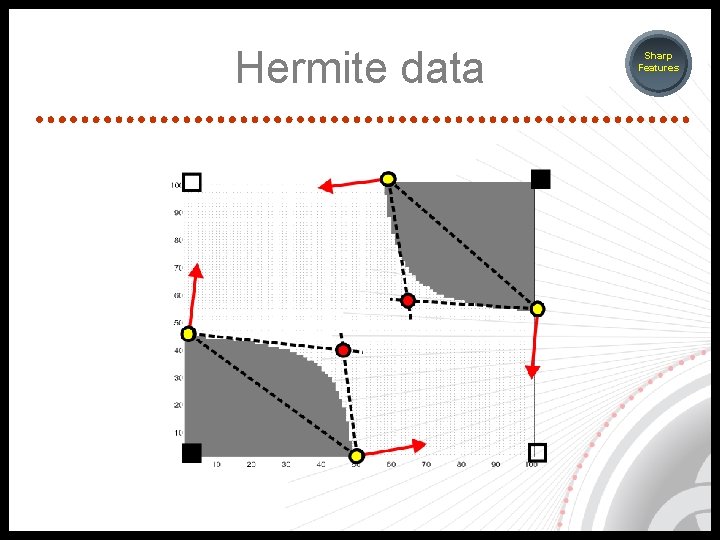
Hermite data Sharp Features
Realtime
Inter-cell dependency Real-time
Previous work & Problems Solutions Results & Conclusions
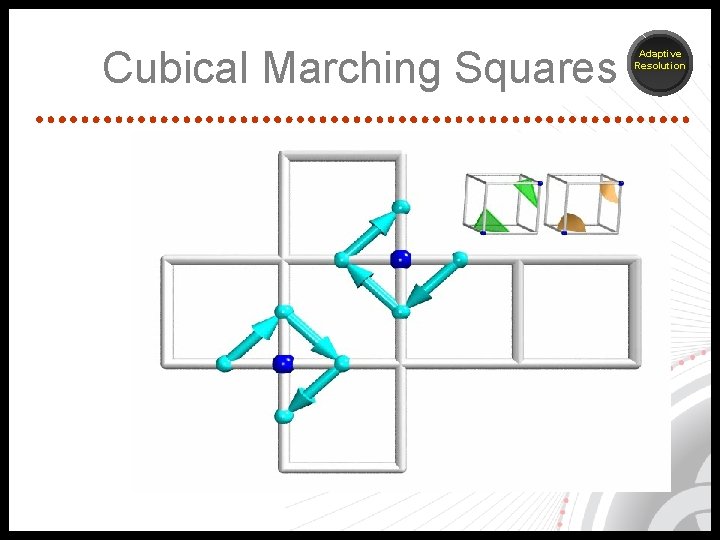
Cubical Marching Squares Adaptive Resolution
CMS Algorithm
CMS Algorithm
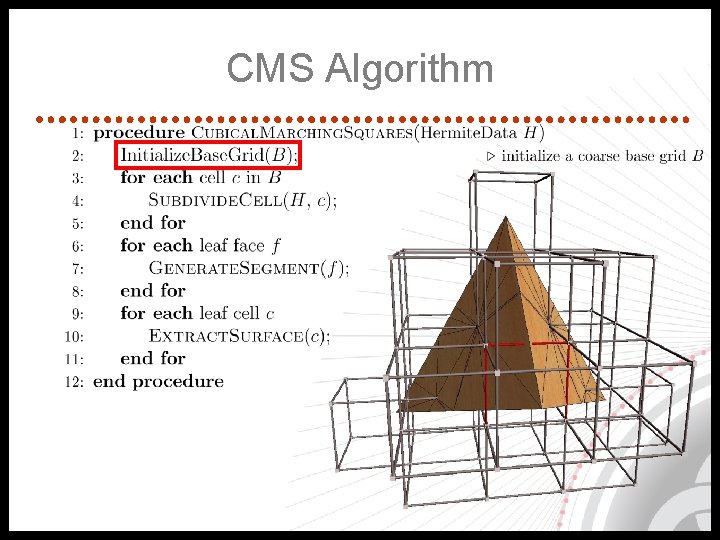
CMS Algorithm
CMS Algorithm
CMS Algorithm
Analysis of face ambiguity • Separated Consistent Topology • Joined
Resolving face ambiguty Consistent Topology
Algorithm – Cubical. Marching. Squares
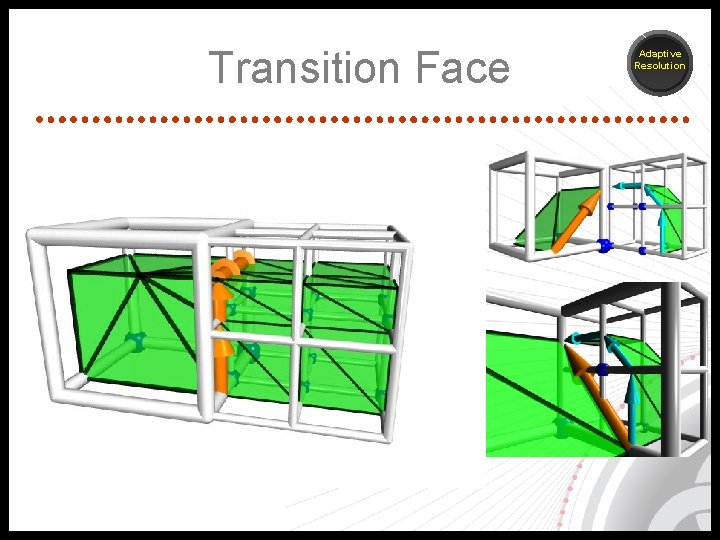
Transition Face Adaptive Resolution
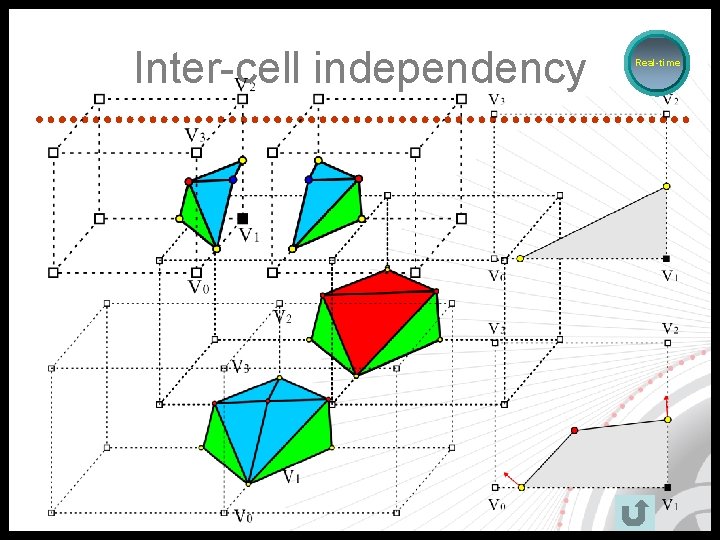
Inter-cell independency Real-time
Previous work & Problems Solutions Results & Conclusions
Simulation • Available shapes • generated randomly in a limited space
Average geometric errors
Error distribution
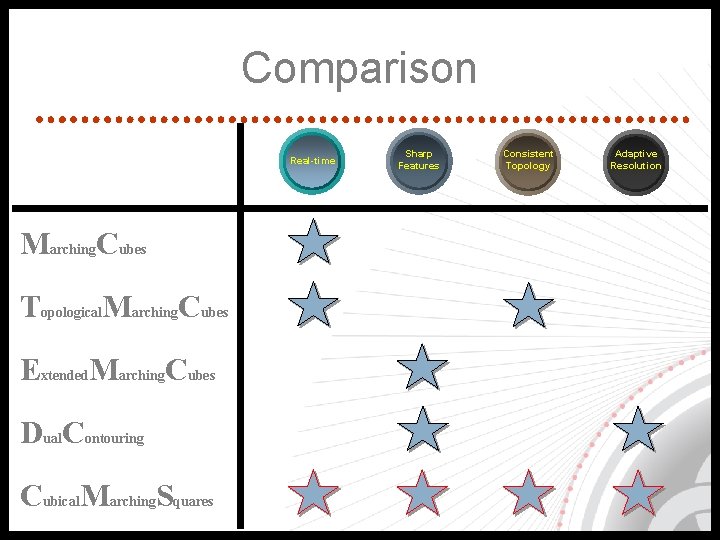
Comparison Real-time Marching. Cubes Topological. Marching. Cubes Extended. Marching. Cubes Dual. Contouring Cubical. Marching. Squares Sharp Features Consistent Topology Adaptive Resolution
Benefits - inter-cell independency 1. Faster 2. Parallelizable 3. Lower Error
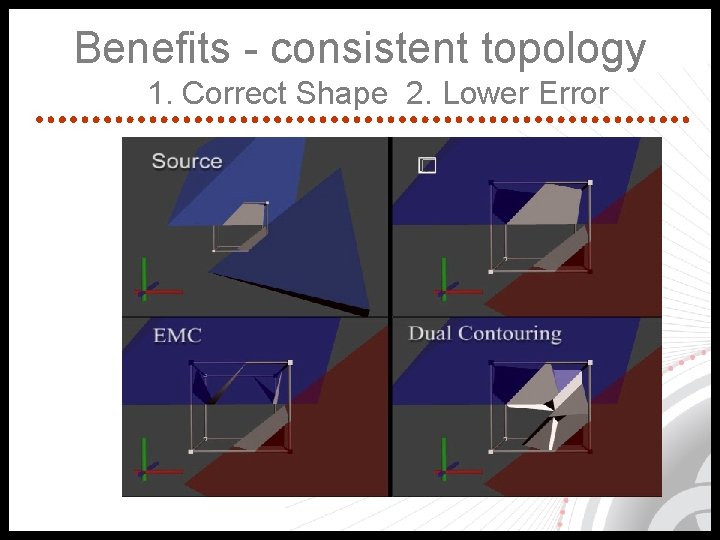
Benefits - consistent topology 1. Correct Shape 2. Lower Error
Benefits - consistent topology 1. Correct Shape 2. Lower Error
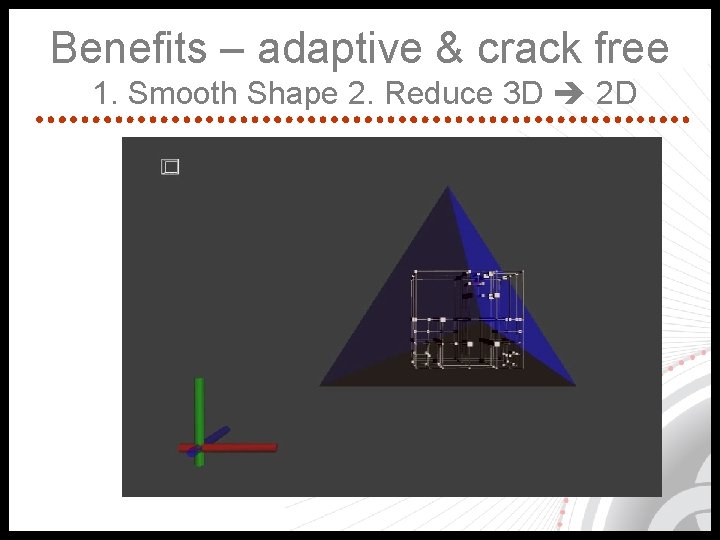
Benefits – adaptive & crack free 1. Smooth Shape 2. Reduce 3 D 2 D
Virtual Sculptor
Remeshing
CSG & LOD
Conclusions Real-time Sharp Features Consistent Topology Adaptive Resolution • Inter-cell dependency is eliminated. • Sharp features are well preserved. • Topologies are well preserved by examining the sharp features. • Our method generates surface adaptively without cracks. • Computation can be accelerated using programmable graphic hardware. • It is easy to incorporate our algorithm into the existing marching cubes implementations.
Acceleration using GPU Real-time
Future work • Full GPU implementation • Applying CMS to distance fields
- Slides: 42