CUBE A Relational Aggregate Operator Generalizing Group By

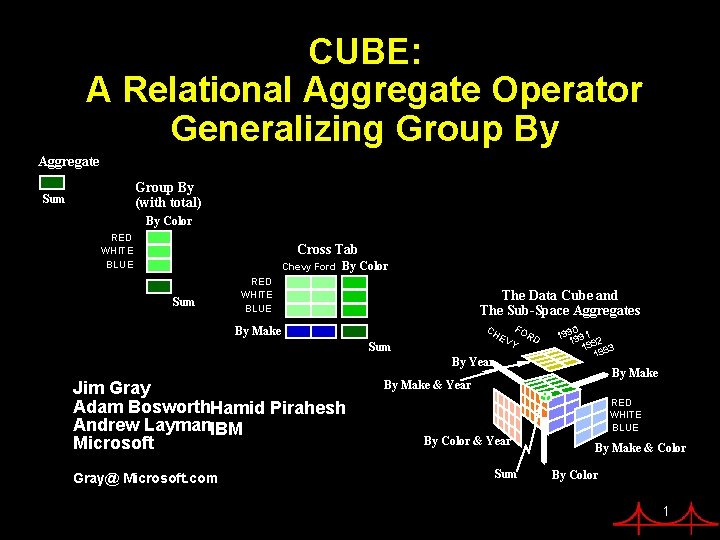
CUBE: A Relational Aggregate Operator Generalizing Group By Aggregate Group By (with total) Sum By Color RED WHITE BLUE Cross Tab Chevy Ford Sum By Color RED WHITE BLUE The Data Cube and The Sub-Space Aggregates CH By Make FO EV Sum Y By Year Jim Gray Adam Bosworth. Hamid Pirahesh Andrew Layman. IBM Microsoft Gray@ Microsoft. com RD 0 199 991 1 992 1 993 1 By Make & Year RED WHITE BLUE By Color & Year Sum By Make & Color By Color 1

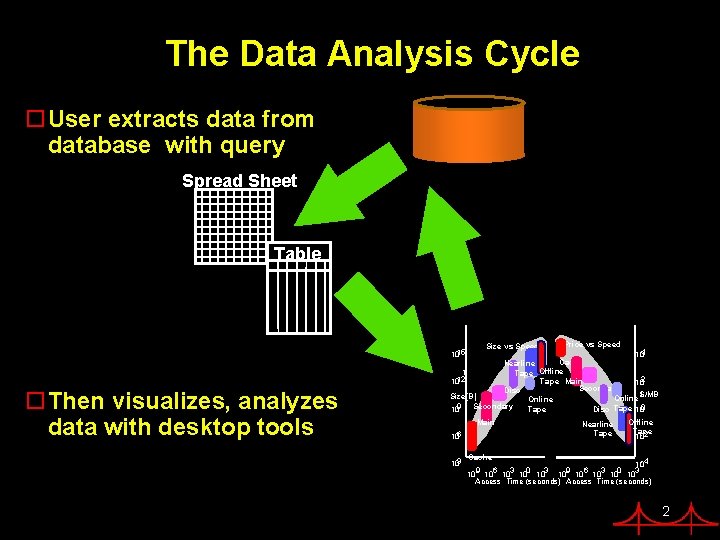
The Data Analysis Cycle o. User extracts data from database with query Spread Sheet Table 1015 o. Then visualizes, analyzes data with desktop tools Size vs Speed Price vs Speed 104 Cache Nearline 1 Tape Offline Tape Main 1012 102 Secondary Disc Size(B) Online $/MB Online Tape 109 Secondary 100 Tape Disc Main 106 Nearline Tape Offline Tape 10 -2 Cache 103 10 -4 -9 -6 -3 0 3 10 10 10 Access Time (seconds) 2

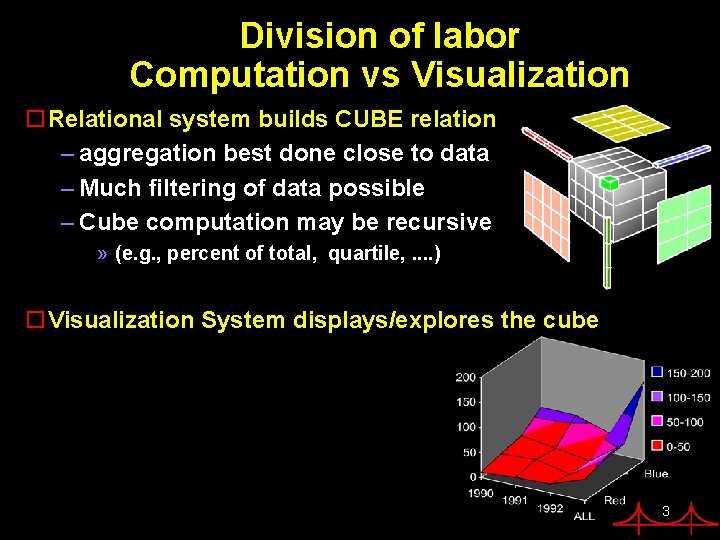
Division of labor Computation vs Visualization o. Relational system builds CUBE relation – aggregation best done close to data – Much filtering of data possible – Cube computation may be recursive » (e. g. , percent of total, quartile, . . ) o. Visualization System displays/explores the cube 3

Relational Aggregate Operators o. SQL has several aggregate operators: – sum(), min(), max(), count(), avg() o. Other systems extend this with many others: – stat functions, financial functions, . . . o. The basic idea is: – Combine all values in a column – into a single scalar value. o. Syntax select sum(units) from inventory; 4

Relational Group By Operator o. Group By allows aggregates over table sub-groups o. Result is a new table o. Syntax: select location, sum(units) from inventory group by location having nation = “USA”; 5

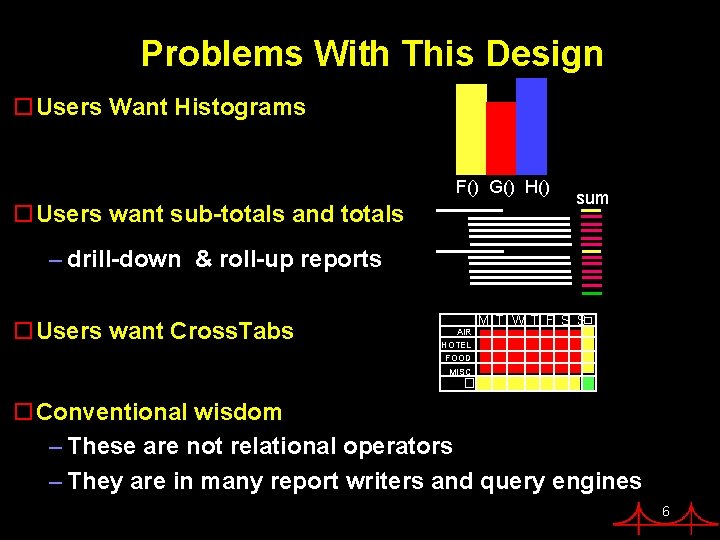
Problems With This Design o. Users Want Histograms F() G() H() o. Users want sub-totals and totals sum – drill-down & roll-up reports o. Users want Cross. Tabs AIR HOTEL FOOD MISC M T W T F S S� � o. Conventional wisdom – These are not relational operators – They are in many report writers and query engines 6

Thesis: The Data CUBE Relational Operator Generalizes Group By and Aggregates 7

The Idea: Think of the N-dimensional Cube Each Attribute is a Dimension o. N-dimensional Aggregate (sum(), max(), . . . ) – fits relational model exactly: » a 1, a 2, . . , a. N, f() o. Super-aggregate over N-1 Dimensional sub-cubes » » ALL, a 2, . . , a. N , f() a 1 , ALL, a 3, . . , a. N , f(). . . a 1, a 2, . . , ALL, f() – this is the N-1 Dimensional cross-tab. o. Super-aggregate over N-2 Dimensional sub-cubes » ALL, a 3, . . , a. N , f() » . . . » a 1, a 2 , . . , ALL, f() 8

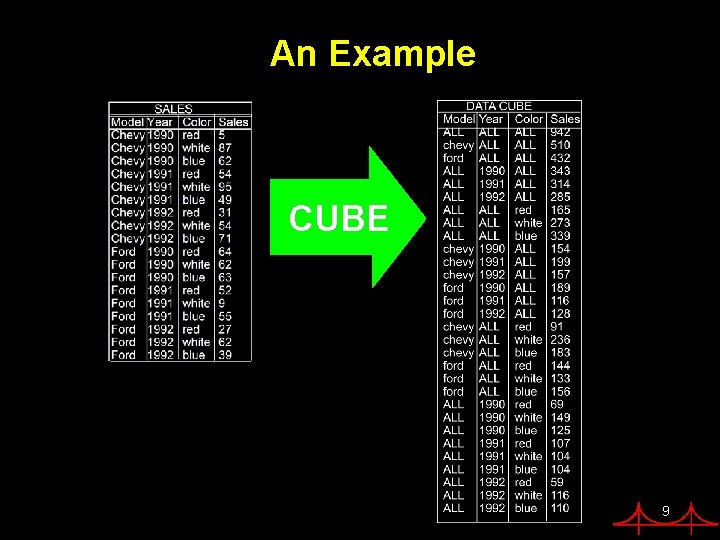
An Example CUBE 9

Why the ALL Value? o. Need a new “Null” value (overloads the null indicator) o. Value must not already be in the aggregated domain o. Can’t use NULL since may aggregate on it. o. Think of ALL as a token representing the set – {red, white, blue}, {1990, 1991, 1992}, {Chevy, Ford} o. Rules for “ALL” in other areas not explored – assertions – insertion / deletion /. . . – referential integrity o. Follow “set of values” semantics. 10

CUBE operator: Syntax o. Proposed syntax: select model, make, year, sum(units) from car_sales where model in {“chevy”, “ford”} and year between 1990 and 1994 group by cube model, make, year having sum(units) > 0; o. Note: Group By operator repeats aggregate list – in select list – in group by list 11

Why This Syntax? oabstract syntax select <field list> <aggregate list> from <table expression> where <search condition> group by [ cube | drill down] <aggregate list> having <search condition> oallows functional aggregations (e. g. , sales by quarter): select store, quarter, sum(units) from sales where nation = “Mexico” group by drill down store, quarter(date) as quarter and year = 1994; 12

Decorations and Abstractions o. Sometimes want to tag cube with redundant values – region #, region_name, sales – region name is not a dimension, it is a decoration – Decorations are functionally dependent on dimensions o. More interesting, some “dimensions” are aggregations. block city county state nation o. Often these aggregations are not linear (are a lattice) second minute hour day week month quarter Xmas Easter Thanksgiving year Holiday o. Rather than treat time as 12 dimensions – Recognize abstractions as one dimension (like decorations) – Compute efficiently (virtual functions) 13

Interesting Aggregate Functions o. From Red. Brick systems – Rank (in sorted order) – N-Tile (histograms) – Running average (cumulative functions) – Windowed running average – Percent of total o. Users want to define their own aggregate functions – statistics – domain specific 14

User Defined Aggregates start Scratchpad end o. Idea: – User function is called at start of each group – Each function instance has scratchpad – Function is called at end of group o. Example: SUM – START: allocates a cell and sets it to zero next – NEXT: adds next value to cell – END: deallocates cell and returns value – Simple example: MAX() o. This idea is in Illustra, IBM’s DB 2/CS, and others o. Needs extension for rollup and cube 15

User Defined Aggregate Function Generalized For Cubes o. Aggregates have graduated difficulty – Distributive: can compute cube from next lower dimension values (count, min, max, . . . ) – Algebraic: can compute cube from next lower scratchpads (average, . . . ) – Holistic: Need base data (Median, Mode, Rank. . ) o. Distributive and Algebraic have simple and efficient algorithm: build higher dimensions from core o. Holistic computation seems to require multiple passes. – real systems use sampling to estimate them » (e. g. , sample to find median, quartile boundaries) 16

How To Compute the Cube? o. If each attribute has Ni values CUBE has P (Ni+1) values o. Compute N-D cube with hash if fits in RAM o. Compute N-D cube with sort if overflows RAM o. Same comments apply to subcubes: – compute N-D-1 subcube from N-D cube. – Aggregate on “biggest” domain first when >1 deep – Aggregate functions need hidden variables: » e. g. average needs sum and count. o. Use standard techniques from query processing – arrays, hashing, hybrid hashing – fall back on sorting. 17

Example: o. Compute 2 D core of 2 x 3 cube o. Then compute 1 D edges o. Then compute 0 D point o. Works for algebraic and distributive functions Saves “lots” of calls 18

Summary o. CUBE operator generalizes relational aggregates o. Needs ALL value to denote sub-cubes – ALL values represent aggregation sets o. Needs generalization of user-defined aggregates o. Decorations and abstractions are interesting o. Computation has interesting optimizations o. Relationship to “rest of SQL” not fully worked out. 19