CST 1101 Problem Solving Using Computers 1 CST

CST 1101 Problem Solving Using Computers 1

CST 1101 Topic 1: Introduction 2

CST 1101 is an OER class • OER: Open Education Resources • All the software and required readings are available on-line and are free • The links to the on-line resources as well as the distribution of chapters across class topics is posted on the CST 1101 City. Tech openlab site: https: //openlab. citytech. cuny. edu/cst 1101 problemsolvingpython/ • The reading materials are free but the reading assignments are mandatory and will be tested as part of programming assignments, tests, and quizzes 3

What problems can be solved by computers? • Problem solving involves: • • Experience Knowledge Process Art • Problem solving is a combination of art and science • Problem = a situation in which one is trying to reach a goal • Problem solving = finding a means for arriving at a goal 4
Logic Puzzles 5
Number Puzzles 6

What does it mean to solve a problem? • In a math class VS using computers • Solving an “instance” vs solving a problem. • Come up with an answer VS come up with a set up steps (an algorithm) that can be understood by a computer write a computer program • A computer program is a collection of instructions that performs a specific task when executed by a computer. • A programmer must be able to do problem manually before programming. 7

What does it mean to solve a problem? • One of the core topics of Computer Science is the study of 'Algorithms'. • What do we mean by an algorithm though? • a series of actions to perform to get a job done. • The study of algorithms is about coming up with such sequences that guarantee particular jobs are done. • It is also about devising efficient ways of doing things. • But the efficiency of algorithms is beyond the scope of this class, it is even beyond the scope of CST courses. 8

Algorithm Example 9

Cooking as Problem Solving • A recipe like a computational process has: • INPUT • STEPS OF A PROCESS • OUTPUTS • How could we write a recipe? • How many times can we execute a recipe? • What is the solution (outcome) of this process? • How many times can we execute this process? • Do we expect a certain outcome? Is the outcome always the same? 10

How to draw a square? • To solve a problem is to give a list of instructions / directions • Let us literally give directions 11

How to draw a square? 4 instructions • Draw the bottom line • Draw the right line • Draw the top line • Draw the left line 12

How to draw TWO squares? 8 instructions • Square 1: Draw the bottom line • Square 1: Draw the right line • Square 1: Draw the top line • Square 1: Draw the left line • Square 2: Draw the bottom line • Square 2: Draw the right line • Square 2: Draw the top line • Square 2: Draw the left line 13

How to draw TWO HUNDRED squares? • 800 instructions? ? • What if we need a thousand squares? 14

Draw a snowflake? https: //studio. code. org/s/frozen/ Puzzles: • • • 3 (sequence) 4 (loop) 5 (nested loop: loop inside a loop) 7 11 13 (circle) 14 (row of circles) 15 (circle of circles) 20 (let your imagination fly) 15

What is an algorithm? • An algorithm is a precise, step-by-step set of instructions for solving a task. • An algorithm does not solve a task; it gives you a series of steps that, if executed correctly, will result in a solution to a task. • Algorithms in every day life: • Starting your car • Logging into your computer • Following a cooking recipe • For an algorithm to be valid, each step (or instruction) must be: • unambiguous – the instruction can only be interpreted in one unique way • executable – the person or device executing the instruction must know how to accomplish the instruction without any extra information. • ordered – the steps of an algorithm must be ordered in a proper sequence to correctly accomplish the task. 16

Problem Solving VS Computer Problem Solving • In a computing problem, we know the “answer”, our goal is to describe the steps of the process to reach the answer for more instances of the problem. • Our solution is not a result, but a series of steps that can be used over many instances of the problem. 17

Stages of Problem Solving (PACT) 1. 2. 3. 4. Problem Definition – Problem identification and representation Analyze – plan a solution Carry out the strategy – execute the plan Test (evaluate the plan and the solution) – determine whether it worked • Which stage can be automated? • Which stage corresponds to writing a program? • Can you think of problems for which you can automate their solution? For which you can create an algorithm? BTW, what is an algorithm 18
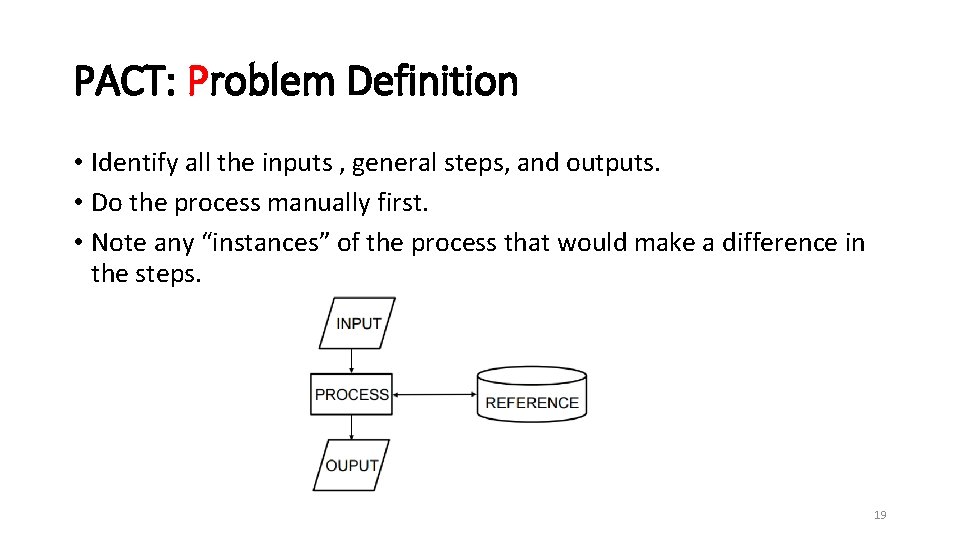
PACT: Problem Definition • Identify all the inputs , general steps, and outputs. • Do the process manually first. • Note any “instances” of the process that would make a difference in the steps. 19

PACT: Analyze • Flow out high-level tasks that may be broken down into small steps. • Categorize the problem based on experience. • Identify any boundaries or special requirements. • Document decision points. 20

PACT: Codify • Identify key elements that are acted upon through the process. • Break the process into small building blocks. • Recognize repetition, and other techniques used in previous processes. • Abstract the problem into computational terms. 21

PACT: Test and Validate • Test the process with instances having solutions you know. • Review the steps for duplication or inefficiency. • Test the process with instances at limits of some steps. • Add further documentation to your description of the steps. 22

Problem Solving and Decomposition • Which one is easier: • Solving one big problem, or • Solving a number of small problems? 23

Problem Solving and Decomposition • Which one is easier: • Solving one big problem, or • Solving a number of small problems? • Decomposition == writing a set of steps • Several levels of decomposition • What are the advantages of small problems? 24

Problem Solving and Decomposition • Which one is easier: • Solving one big problem, or • Solving a number of small problems? • Decomposition == writing a set of steps • Several levels of decomposition • What are the advantages of small problems? • Easier to solve • Easier to ensure the solution is correct • In order to have a number of small problems: • What do we need to do first? 25

Common Mistake • Dive into the details • (e. g. at the level of Python instructions) • Do not consider decomposing the problem first • “in English” 26

Tic-tac-toe • We would like to build a tic-tac-toe game interface for two people to play. The interface is a referee who ensures that both players follow the rules and announces the winner. • • What is the initial input? What is the output? Are there any intermediate inputs and outputs? How would you decompose the problem? 27

Problem Decomposition 1. Display the board 2. Make a move 3. Decide winner Can these smaller problems be independently • solved? • tested? 28

Declare the Winner Seems to be complicated, what can we do? Decompose! • Check 3 rows • Check 3 columns • Check 2 diagonals Can they be independently • Solved? • Tested? 29

Top-down Decomposition 1. Display the board 2. Make a move 3. Decide winner • Check 3 rows • Check 3 columns • Check 2 diagonals 30

Make a Move • Decompose: • Ask for a move • Check the validity of the move • Update the board 31

Top-down Decomposition 1. Display the board 2. Make a move • Ask for a move • Check the validity of the move • Update the board 3. Decide winner • Check 3 rows • Check 3 columns • Check 2 diagonals 32

When to stop decomposing a problem? • Until you’re confident you can solve the smaller problems correctly • Different for different people 33

An algorithm for solving a maze. • To simplify the problem, we deal with mazes containing no loops are known as "simply connected“ • Random mouse algorithm • Wall follower 34

Random mouse algorithm This is a trivial method that can be implemented by a very unintelligent robot or perhaps a mouse. It is simply to proceed following the current passage until a junction is reached, and then to make a random decision about the next direction to follow. Although such a method would always eventually find the right solution, this algorithm can be extremely slow. 35

• Can you write a set of steps for a computer to follow? • Use this algorithm and show a computer will use it to go through a maze. 36
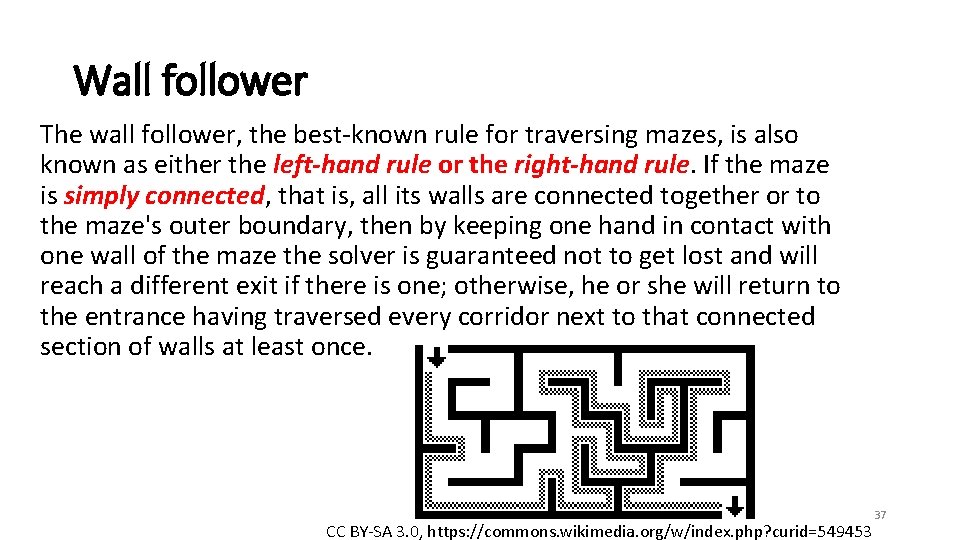
Wall follower The wall follower, the best-known rule for traversing mazes, is also known as either the left-hand rule or the right-hand rule. If the maze is simply connected, that is, all its walls are connected together or to the maze's outer boundary, then by keeping one hand in contact with one wall of the maze the solver is guaranteed not to get lost and will reach a different exit if there is one; otherwise, he or she will return to the entrance having traversed every corridor next to that connected section of walls at least once. CC BY-SA 3. 0, https: //commons. wikimedia. org/w/index. php? curid=549453 37

• Can you write a set of steps (algorithm) for a computer to follow? • Use this algorithm and show a computer will use it to go through a maze. 38
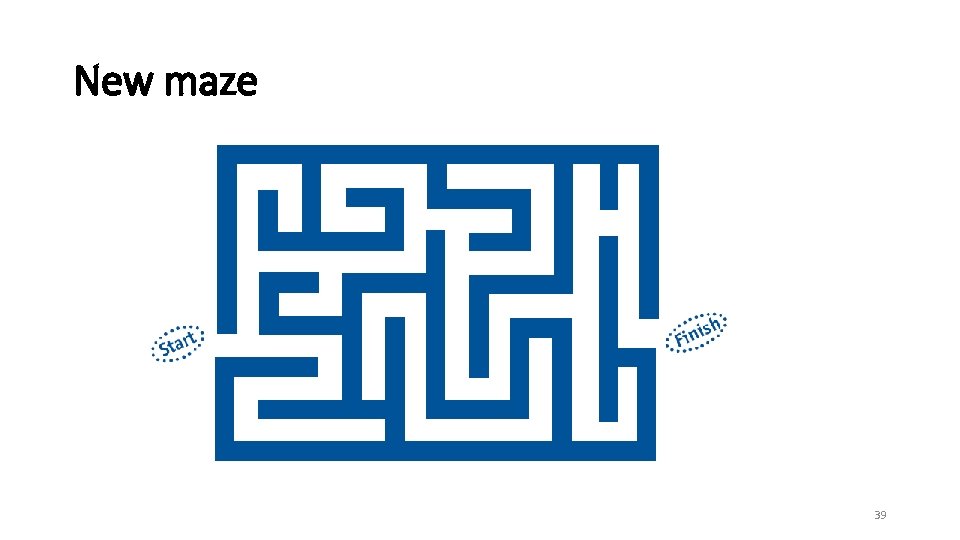
New maze 39
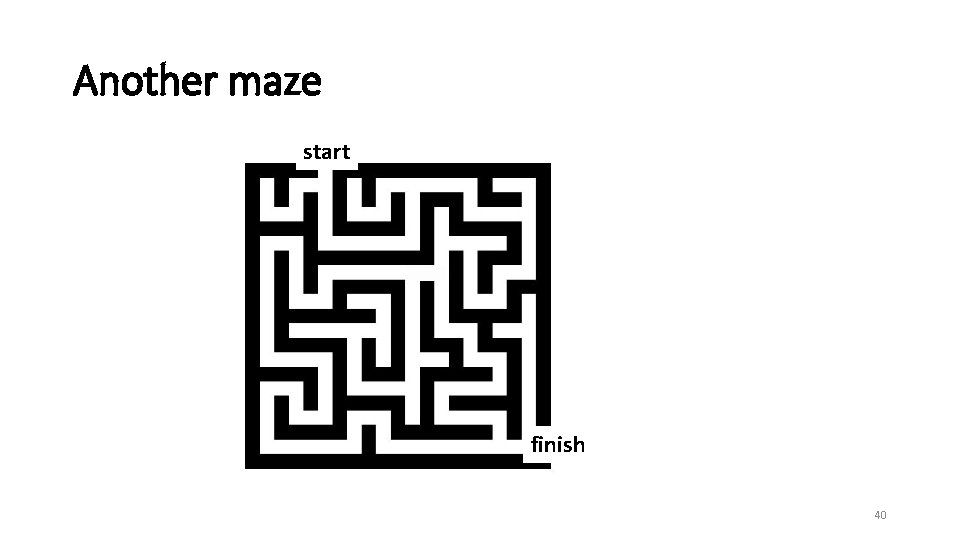
Another maze start finish 40
Yes another maze finish start 41

Questions • Are the solutions (traces) for different mazes identical? • Can you use the same algorithm for different mazes? 42

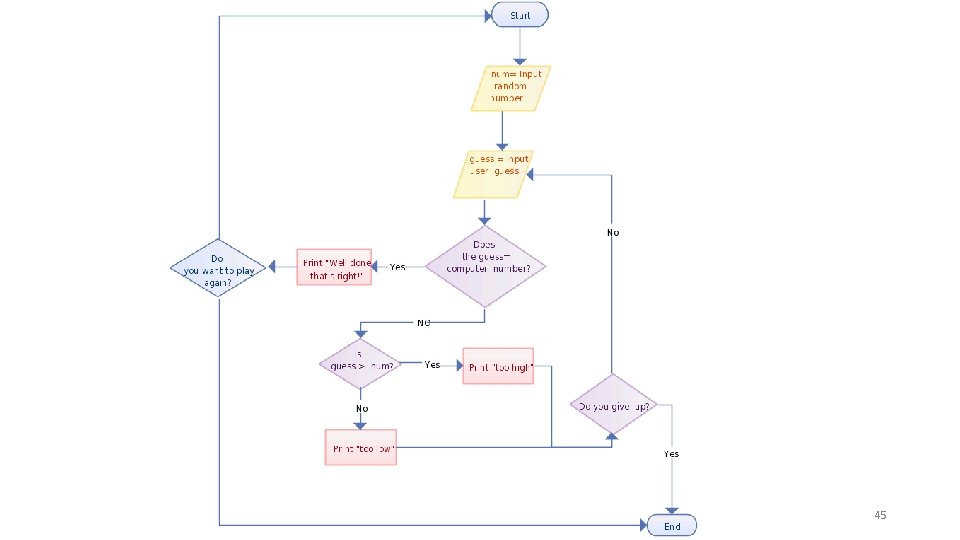
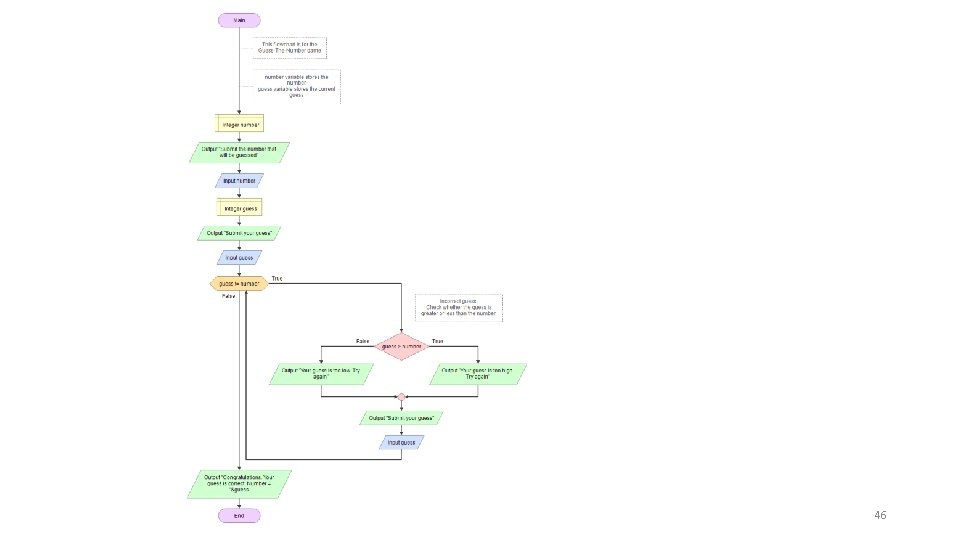
Why are Algorithms Important? • An algorithm documents the "how to" for accomplishing a particular task. • If an algorithm is written well, it can be used to accomplish not only a single task but a whole group of related tasks. • The existence of an algorithm means that the task can potentially be automated (i. e. , performed by a computer). One of the common ways to express algorithms without using a programming language is called flowcharting 43

Guess-my-number • In the "guess-my-number" game, one player (player A) makes guesses at another player's (player B) secret number. All games would follow the following procedure: • Player B decides on a number between a known, set limit (for example, he/she may only choose a number between 1 and 100), this will become the player's "secret number" (the secret number must be an integer) • Player A then guesses an initial number • Player B responds by (honestly) declaring Player A's response to be either too high, too low, or correct • The process repeats, Player A guesses a number based on previous feedback, and Player B responds, until Player A guesses correctly How would you play this game? 44
45
46

Can you optimize the suggested solution? 47
- Slides: 47