CSNB 234 ARTIFICIAL INTELLIGENCE Chapter 3 Propositional Logic

CSNB 234 ARTIFICIAL INTELLIGENCE Chapter 3 Propositional Logic & Predicate Logic UNIVERSITI TENAGA NASIONAL 1

EARLY DEVELOPMENT OF SYMBOLIC LOGIC criticised • English mathematician De. Morgan traditional logic because it was written in natural language. • He thought that the formal meaning of a syllogistic statement was confused by the semantics of natural language. • De. Morgan and Boole both contributed to the development of Propositional Logic (or Propositional Calculus). • Using familiar algebraic symbols, they showed how certain algebraic rules were equally applicable to numbers, set and truth values of propositions. UNIVERSITI TENAGA NASIONAL 2

¨ Definition Propositional Logic – Propositional Logic Sentences (I) • Every propositional symbol and truth symbol is a sentence. – For example: true, P, Q, and R are four sentences • The negation of a sentence is a sentence – For example: P and false are sentences • The conjunction (and) of two sentences is a sentence – For example: P P is a sentence UNIVERSITI TENAGA NASIONAL 3

Propositional Logic ¨Propositional Logic Sentences (II) • The disjunction (or) of two sentence s is a sentence – For example: P P is a sentence • The implication of one sentence for another is a sentence – For example: P Q is a sentence • The equivalence of two sentences is a sentence – for example: P Q = R is a sentence UNIVERSITI TENAGA NASIONAL 4

Propositional Logic Semantics An interpretation of a set of propositions is the assignment of a truth value, either T of F, to each propositional symbol. The interpretation or truth value for sentences is determined by: The truth assignment of negation, P, where P is any propositional symbol, is F if the assignment to P is T and T if the assignment to P is F. The truth assignment of conjunction, , is T only when both conjuncts have truth value T; otherwise it is F. UNIVERSITI TENAGA NASIONAL 5

Propositional Calculus Semantics The truth assignment of disjunction, , is F only when both conjuncts have truth value F; otherwise it is T. The truth assignment of implication, , is F only when the premise or symbol before the implication is T and the truth value of the consequent or symbol after the implication is F; otherwise it is always T. The truth assignment of equivalence, =, is T only when both expressions have the same truth assignment for all possible interpretations; otherwise it is F. UNIVERSITI TENAGA NASIONAL 6

Prove that ((P Q R) = P Q R is a well-formed sentence in the propositional calculus. Answer. Since: P, Q and R are propositions and thus sentences P Q, the conjunction of two sentences, is a sentence (P Q) R, the implication of a sentence for another, is a sentence UNIVERSITI TENAGA NASIONAL 7

P, Q and R are propositions and thus sentences P and Q , the negation of two sentences, are sentences P Q, the disjunction of two We get back the sentences, is a sentence original P Q R, the disjunction of two sentences, is a sentence ((P Q) R) = P Q R, the equivalence of two sentences, is a sentence UNIVERSITI TENAGA NASIONAL 8

CONCLUSION FOR THE WORKED EXAMPLE The above is our original sentence, which has been constructed through a series of applications of legal rules and is therefore well-formed. UNIVERSITI TENAGA NASIONAL 9

¨Constants refer to atomic propositions. raining snowing eating hungry wet ¨Compound sentences capture relationships among propositions. ¨raining snowing wet UNIVERSITI TENAGA NASIONAL 10

¨ Negations: ¬ raining ¨ The argument of a negation is called the target. ¨ Conjunctions: (raining snowing ) ¨ The arguments of a conjunction are called conjuncts. ¨ Disjunctions: (raining snowing ) ¨ The arguments of a disjunction are called disjuncts. UNIVERSITI TENAGA NASIONAL 11

¨ Implications: (raining cloudy ) Compound Sentences – The left argument of an implication is the antecedent. – The right argument of an implication is called the consequent. ¨ Reductions: cloudy raining – The left argument of a reduction is the consequent. – The right argument of a reduction is called the antecedent. ¨ Equivalences: raining cloudy UNIVERSITI TENAGA NASIONAL 12

Some Laws. OF for Logic Use RULES ALGEBRAIC MANIPULATION x y=y x Commutativity x y=y x x (y z) = (x y) z Associativity x (y z) = (x y) z x (y z) = (x y) (x z) Distributivity x (y z) = (x y) (x z) UNIVERSITI TENAGA NASIONAL 13

Semantics of Logical Operators ¨ Negation: ¨ Conjunction: P P T F F T P Q P T T F F T F T F F F Q UNIVERSITI TENAGA NASIONAL 14

Semantics of Logical Operators ¨ Disjunction: P Q P T T F F T F T T T F Q UNIVERSITI TENAGA NASIONAL 15

More Semantics of Logical Operators Implication: P Q T T F F T F P Q T F T T Reverse Implication: Equivalence: P Q Q P T T F F T F T F F T P Q T T F F T F UNIVERSITI TENAGA NASIONAL Q P T T F T 16

Satisfaction ¨ An interpretation i satisfies a sentence φ (written |=i φ ) if and only if φ i =T. ¨ A sentence is satisfiable if and only if there is some interpretation that satisfies it. ¨ A sentence is valid if and only if every interpretation satisfies it. ¨ A sentence is unsatisfiable if and only if there is no interpretation that satisfies it. UNIVERSITI TENAGA NASIONAL 17

Truth Tables A truth table is a table of all possible values for a set of propositional constants. p T T F F q T T F F r T F T F Each interpretation of a language is a row in the truth table for that language. For a propositional language with n logical constants, there are 2 n interpretations. UNIVERSITI TENAGA NASIONAL 18

Logical Equivalence Two sentences are logically equivalent if and only if they logically entail each other. Examples: ¬(¬p) ¬(p q ) p ¬p ¬q ¬p q de Morgan’s law UNIVERSITI TENAGA NASIONAL 19

Problems ¨ There can be many, many interpretations for a propositional language. ¨ Remember that, for a language with n constants, there are 2 n possible interpretations. ¨ Sometimes there are many constants among premises that are irrelevant to the conclusion. --- Much work wasted. Solution: use other kind of proof theory, such as refutation proof (later part) UNIVERSITI TENAGA NASIONAL 20

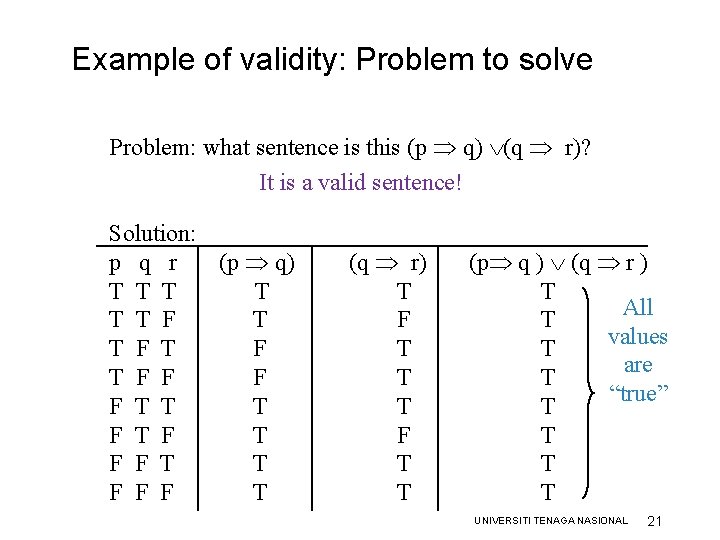
Example of validity: Problem to solve Problem: what sentence is this (p q) (q r)? It is a valid sentence! Solution: p q r (p q) T T T F T F F T T T F T F F T T F F F T (q r) T F T T (p q ) (q r ) T All T values T are T “true” T T UNIVERSITI TENAGA NASIONAL 21

CLAUSAL FORM Propositional resolution works only on expressions in clausal form. Fortunately, it is possible to convert any set of propositional calculus sentences into an equivalent set of sentences in clausal form. UNIVERSITI TENAGA NASIONAL 22

CONVERSION TO CLAUSAL FORM Implications Out: P Q P Q P Q ( P Q) (P Q ) Negations In: P (P Q) (P Q ) P P Q P Q UNIVERSITI TENAGA NASIONAL 23

Predicate Calculus (=Predicate Logic) UNIVERSITI TENAGA NASIONAL 24

PREDICATE CALCULUS (I) In Proposition Logic, each atomic symbol (P, Q, etc) denotes a proposition of some complexity. There is no way to access the components of an individual assertion. Through inference rules we can manipulate predicate calculus expressions, accessing their individual components and inferring new sentences. UNIVERSITI TENAGA NASIONAL 25

PREDICATE CALCULUS (II) In Predicate Calculus, there are two ways variables may be used or quantified. In the first, the sentence is true for all constants that can be substituted for the variable under the intended interpretation. The variable is said to be universal quantified. Variables may also be quantified existentially. In this case the expression containing the variable is said to be true for at least one substitution from the domain of definition. Several relationships between negation and the universal and existential quantifiers are given below: UNIVERSITI TENAGA NASIONAL 26

PREDICATE CALCULUS (III) Predicate calculus sentences Every atomic sentence is a sentence if s is a sentence, then so is its negation, s if s 1 and s 2 are sentences, then so is their conjunction, s 1 s 2 if s 1 and s 2 are sentences, then so is their disjunction, s 1 s 2 if s 1 and s 2 are sentences, then so is their implication, s 1 s 2 if s 1 and s 2 are sentences, then so is their equivalence, s 1 = s 2 UNIVERSITI TENAGA NASIONAL 27

PREDICATE CALCULUS (IV) If X is a variable and s is a sentence, then X s is a sentence UNIVERSITI TENAGA NASIONAL 28

ENGLISH SENTENCES REPRESENTED IN PREDICATE CALCULUS: Some people like fried chicken. X (people(X) likes(X, fried_chicken)). Nobody likes income taxes. X likes(X, income_taxes). X likes(X, income_taxes). UNIVERSITI TENAGA NASIONAL 29

Rules: All students passed examination. X (student(X) pass_exam(X)) All purple mushrooms are poisonous. X (purple(X) mushroom(X) poisonous(X)) Facts: Tom loves Jerry. loves(tom, Jerry). Ali is a student(ali). UNIVERSITI TENAGA NASIONAL 30

EXERCISE #1: TRANSLATE THE FOLLOWING ENGLISH STATEMENTS INTO PREDICATE EXPRESSIONS Batman is knowledgeable and he is wealthy. All people that are not poor are happy. Students who like to read books are intelligent. Tweety can fly if it is not fried and has wings. UNIVERSITI TENAGA NASIONAL 31

Exercise #2 1. Everybody likes something. 2. There is something whom everybody likes. UNIVERSITI TENAGA NASIONAL 32

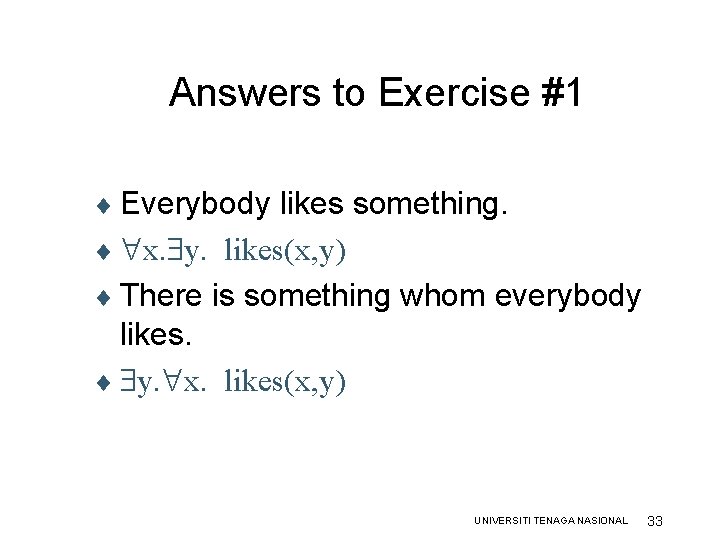
Answers to Exercise #1 ¨ Everybody likes something. ¨ x. y. likes(x, y) ¨ There is something whom everybody likes. ¨ y. x. likes(x, y) UNIVERSITI TENAGA NASIONAL 33

Exercise #3 For predicates p & q, and variables X and Y: Write the following in English X p(X) = X p(X) Y q(Y) = Y q(Y) UNIVERSITI TENAGA NASIONAL 34

EXERCISE #4: CONVERT EACH OF THE FOLLOWING PREDICATE LOGIC TO ENGLISH SENTENCES food(laksa) X loves(X, superman) loves(superman, X) X food(X) like(arul, X) X eat(haswan, X) eat(hasman, X) X Y eat(X, Y) alive(X) food(Y) UNIVERSITI TENAGA NASIONAL 35

Exercise #5 ¨ Convert each of the following into Predicate Calculus equivalence: – – – – Marcus was a man Marcus was a Pompeian All Pompeians were Romans Caesar was a ruler All Romans were either loyal to Caesar or hated him Everyone is loyal to someone people only try to assassinate rulers they are not loyal to Marcus tried to assassinate Caesar UNIVERSITI TENAGA NASIONAL 36

Predicate logic for the 8 facts in Exercise #5 1. 2. 3. 4. 5. 6. 7. 8. man(Marcus) pompeian(Marcus) X. pompeian(X) roman(X) ruler(Caesar) X. roman(X) loyalto(X, Caesar) hate(X, Caesar) X. Y. loyalto(X, Y) X. Y. person(X) ruler(Y) tryassassinate(X, Y) loyalto(X, Y) tryassasinate(Marcus, Caesar) 9. X. man(X) person(X) UNIVERSITI TENAGA NASIONAL 37

Answers to Exercise #5 loyato(Marcus, Caesar) (using 7, substitution, & apply M. P) person(Marcus) tryassassinate(Marcus, Caesar) ruler(Caesar) using (4) person(Marcus) tryassassinate(Marcus, Caesar) using (8) person(Marcus) (using 9, substitution & apply M. P) man(Marcus) using (1) nil UNIVERSITI TENAGA NASIONAL 38

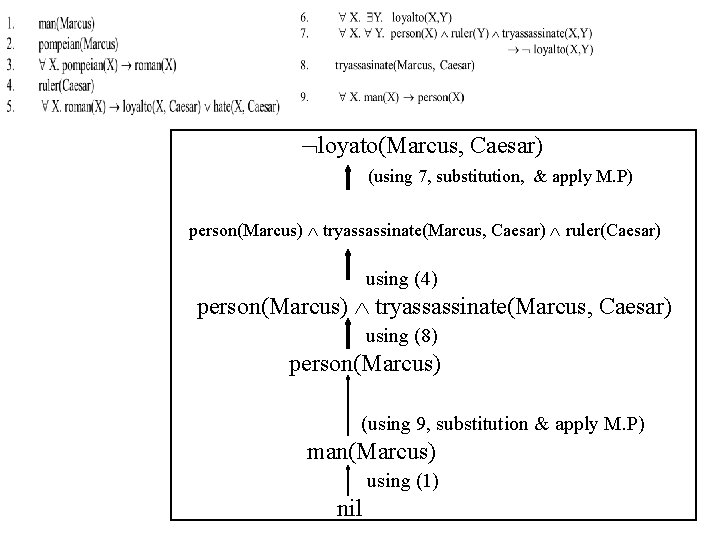
loyato(Marcus, Caesar) (using 7, substitution, & apply M. P) person(Marcus) tryassassinate(Marcus, Caesar) ruler(Caesar) using (4) person(Marcus) tryassassinate(Marcus, Caesar) using (8) person(Marcus) (using 9, substitution & apply M. P) man(Marcus) using (1) nil

Towards the Resolution and Refutation Proof UNIVERSITI TENAGA NASIONAL 40

Stages involved in Proof Theory ¨ Stage 1 – convert all axioms into prenex form • i. e. all quantifiers are at the front ¨ Stage 2 – purge existential quantifiers – this process is known as skolemization ¨ Stage 3 – drop universal quantifiers • as they convey no information UNIVERSITI TENAGA NASIONAL 41

An Example Consider the arguments: All men are mortal Superman is a man Superman is mortal (given premise) (goal to test) The argument gets formalised as: X man(X) mortal(X) man(Superman) mortal(Superman) (goal) Negation of goal And has, as its conflict set in Clausal form: man(X) mortal(X) ---- (1) man(Superman) ---- (2) mortal(Superman) ---- (3) UNIVERSITI TENAGA NASIONAL 42

Apply resolution to derive at a contradiction: We get: man(Superman) and, direct contradiction from (1) & (3) from (2) & (4) The conclusion is that “the goal is true” (i. e. superman is mortal) UNIVERSITI TENAGA NASIONAL 43